
STATE ESTIMATION OF NONLINEAR DISCRETE-TIME SYSTEMS
BASED ON THE DECOUPLED MULTIPLE MODEL APPROACH
Rodolfo Orjuela, Beno
ˆ
ıt Marx, Jos
´
e Ragot and Didier Maquin
Centre de Recherche en Automatique de Nancy, UMR 7039, Nancy-Universit
´
e, CNRS
2, Avenue de la For
ˆ
et de Haye, 54 516 Vandœuvre-l
`
es-Nancy, France
Keywords:
State estimation, nonlinear discrete-time systems, multiple model approach, decoupled multiple model.
Abstract:
Multiple model approach is a powerful tool for modelling nonlinear systems. Two structures of multiple mod-
els can be distinguished. The first structure is characterised by decoupled submodels, i.e. with no common
state (decoupled multiple model), in opposition to the second one where the submodels share the same state
(Takagi-Sugeno multiple model). A wide number of research works investigate the state estimation of nonlin-
ear systems represented by a classic Takagi-Sugeno multiple model. On the other hand, to our knowledge, the
state estimation of the decoupled multiple model has not been investigated extensively. This paper deals with
the state estimation of nonlinear systems represented by a decoupled multiple model. Conditions for ensuring
the convergence of the estimation error are formulated in terms of a set of Linear Matrix Inequalities (LMIs)
employing the Lyapunov direct method.
1 INTRODUCTION
Highly nonlinear processes are commonly encoun-
tered in practical engineering problems (chemistry,
mechanic, hydraulic, electrotechnics, etc). An accu-
rate model with a simple structure, preferably linear,
is often necessary for designing a control law or set-
ting up a diagnosis strategy using conventional con-
trol tools. Building only one model, valid in whole
operating space of the system, is not always possible
due, for example, to the change of the dynamic be-
haviour in the operating space. Hence, the operating
space of the system is often limited before the identi-
fication stage (local modelling).
New techniques of identification have been devel-
oped for modelling the overall behaviour of the pro-
cess (global modelling). One of these techniques is
based on the decomposition of the operating space of
the system into a finite number of operating zones.
Each operating zone is characterised by a submodel
that has a simple structure. According to the zone
where the nonlinear system evolves, the output y
i
of
each submodel is more or less requested in order to
describe the global behaviour y of the nonlinear sys-
tem, that is to say:
y(k) =
L
∑
i=1
µ
i
(k)y
i
(k), (1)
where the i
th
submodel contribution depends on the
weighting function µ
i
. A wide number of identifi-
cation techniques based on this same principle can
be distinguished: piecewise linear model, radial ba-
sis function networks, fuzzy models, multiple models,
etc.
In this communication, we tackle the multiple
model approach. Classically, the multiple model is
built using linear submodels associated with weight-
ing functions that ensure a smooth blend between the
submodels. It is important to note that the multi-
ple models are considered as an universal approxima-
tion tool of nonlinear systems (Johansen et al., 2000).
Hence, it is possible to apply the available tools for
linear systems to nonlinear systems represented by a
multiple model.
In (Filev, 1991) two possible interpretations of
equation (1) have been investigated in a fuzzy mod-
elling framework (these interpretations will be di-
rectly related to multiple model). In the first inter-
pretation, the submodels are decoupled and their state
vector is different (decoupled multiple model); in the
second one, the submodels have the same state vector
(Takagi-Sugeno multiple model).
The second interpretation has been widely popu-
larized and many works deal with the identification
and analysis (control, state estimation, diagnosis, etc.)
of nonlinear systems represented by this class of mul-
142
Orjuela R., Marx B., Ragot J. and Maquin D. (2007).
STATE ESTIMATION OF NONLINEAR DISCRETE-TIME SYSTEMS BASED ON THE DECOUPLED MULTIPLE MODEL APPROACH.
In Proceedings of the Fourth International Conference on Informatics in Control, Automation and Robotics, pages 142-148
DOI: 10.5220/0001640101420148
Copyright
c
SciTePress

tiple model.
By comparison with the Takagi-Sugeno multi-
ple model, the decoupled multiple model has been
less investigated. Some works in control domain
(Gawthrop, 1995; Gatzke and Doyle III, 1999; Gre-
gorcic and Lightbody, 2000) and in identification
(Venkat et al., 2003) of nonlinear systems have em-
ployed successfully this structure and shown its rele-
vance. However, to our knowledge the state estima-
tion problem has not been investigated.
In this paper, a new method for designing a state
estimator of nonlinear discrete-time systems repre-
sented by a decoupled multiple model is presented.
The paper starts with section 2 that introduces two
multiple model structures according to the selected
interpretation. Stability of decoupled multiple model
is investigated in section 3. In section 4, sufficient
conditions (in LMIs terms) are established in order to
ensure the asymptotic convergence of the estimation
error. Finally, section 5 presents an academic example
of state estimation of a decoupled multiple model.
2 MULTIPLE MODEL
STRUCTURES
The interconnection of the submodels can be per-
formed with various structures in order to generate
the global output of the multiple model. Two essen-
tial structures of multiple models can be distinguished
whether the same state vector appears in all submod-
els or not.
Concerning the identification step, there exists dif-
ferent techniques (linearisation, parametric optimisa-
tion) for the parameter estimation of the submod-
els for a particular multiple model structure. See
(Murray-Smith and Johansen, 1997; Gasso et al.,
2001; Venkat et al., 2003) and the references therein
for further information about these techniques.
2.1 Takagi-Sugeno Multiple Model
The Takagi-Sugeno multiple model structure is con-
ventionally employed in multiple model analysis and
synthesis (Murray-Smith and Johansen, 1997). This
multiple model has the following structure:
x
i
(k+ 1) = A
i
x(k) + B
i
u(k),
x(k+ 1) =
L
∑
i=1
µ
i
(ξ(k))x
i
(k+ 1), (2)
y(k) =
L
∑
i=1
µ
i
(ξ(k))C
i
x(k),
where x ∈ R
n
is the state vector, u ∈ R
m
the input
and y ∈ R
p
the output vector. For the i
th
submodel,
A
i
∈ R
n×n
is the system matrix, B
i
∈ R
n×m
the input
matrix andC
i
∈ R
p×n
the output matrix. The µ
i
are the
weighting functions with the following properties:
L
∑
i=1
µ
i
(ξ(k)) = 1, ∀k (3a)
0 ≤ µ
i
(ξ(k)) ≤ 1 ∀i = 1...L, ∀k (3b)
ξ is the decision variable that depends, for example,
on the measurable state variable and/or input or output
of the system.
From equation (2), one can see that in the Takagi-
Sugeno multiple model there is a common state x that
couples all submodel states x
i
. Therefore the dimen-
sion of the state vectors must be identical for all the
submodels.
2.2 Decoupled Multiple Model
Another possible structure using a parallel intercon-
nection of the submodels is proposed in (Filev, 1991).
Here, this structure is slightly modified using a state
representation as follows:
x
i
(k+ 1) = A
i
x
i
(k) + B
i
u(k),
y
i
(k) = C
i
x
i
(k) (4)
y(k) =
L
∑
i=1
µ
i
(ξ(k))y
i
(k),
where x
i
∈ R
n
i
and y
i
∈ R
p
are, respectively, the state
vector and the output vector for the i
th
submodel and
where u, y, ξ, A
i
∈ R
n
i
×n
i
, B
i
∈ R
n
i
×m
et C
i
∈ R
p×n
i
have been defined in the previous section.
It should be noted that the global output of the
multiple model is given by a weighted sum of the
submodel outputs. The blending between the sub-
models is made through the static equation. There-
fore each submodel evolves independently in its own
state space according to the input control and its ini-
tial state.
It is obvious that the principal interest of this
structure is the decoupling between the submodels.
Indeed, in contrast to the Takagi-Sugeno multiple
model, in the decoupled multiple model the dimen-
sion of the state vector x
i
of each submodel can be dif-
ferent (of course the output vector dimension must be
identical). Therefore, this structure is well adapted for
modelling strongly nonlinear systems whose structure
varies with the operating zone.
Notation: The following notations will be used all
along this paper. P > 0 (P < 0) means P is a positive
(negative) definite matrix; P
T
denotes the transpose
of P. We shall simply write µ
i
(ξ(k)) = µ
i
(k).
STATE ESTIMATION OF NONLINEAR DISCRETE-TIME SYSTEMS BASED ON THE DECOUPLED MULTIPLE
MODEL APPROACH
143

3 STABILITY ANALYSIS
It is possible to rewrite the equations (4) using an aug-
mented state vector as follows:
x(k+ 1) =
˜
Ax(k) +
˜
Bu(k),
y(k) =
˜
C(k)x(k), (5)
where:
˜
A =
A
1
0 0 0 0
0
.
.
.
0 0 0
0 0 A
i
0 0
0 0 0
.
.
.
0
0 0 0 0 A
L
,
˜
B =
B
1
.
.
.
B
i
.
.
.
B
L
,
˜
C(k) =
µ
1
(k)C
1
.
.
.
µ
i
(k)C
i
.
.
.
µ
L
(k)C
L
T
and x(k) = [
x
1
(k) ··· x
i
(k) ··· x
L
(k)
]
T
∈ R
n
, n =
L
∑
i=1
n
i
.
Comments
• The matrices
˜
A and
˜
B are partitioned block matri-
ces.
• The output matrix
˜
C(k) is a partitioned blocks ma-
trix whose parameters vary with time. Indeed,
the weighting functions µ
i
(k) only affect the sub-
model outputs.
The stability of a decoupled multiple model can be
easily established by analysing the eigenvalues of the
matrix
˜
A. Notice that the matrix
˜
A is a block diagonal
matrix. Therefore, all eigenvalues of this matrix are
inside the unit circle if and only if all eigenvalues of
every matrices A
i
are inside the unit circle.
To sum up, a decoupled multiple model is stable
if and only if all submodels are stable, in contrast to
Takagi-Sugeno multiple model where the stability de-
pends not only on the stability of the submodels but
also on the weighting function values. In the sequel,
the multiple model is assumed to be stable.
4 STATE ESTIMATION
State estimation of Takagi-Sugeno multiple model has
been widely investigated in a stabilisation law control
design perspective (Tanaka and Sugeno, 1990; Feng
et al., 1997; Chadli et al., 2003; Guerra and Ver-
meiren, 2004). Indeed, most of the used control tech-
niques needs the state vector knowledge which is not
in general fully measurable.
The classically used state estimator is an extension
of the proportional (Luenberger) observer. However,
some other classes of state estimators have been de-
veloped, for example, sliding mode observers (Palm
and Bergstern, 2000) and unknown input observers
(Akhenak et al., 2004).
The Lyapunov second method is typically em-
ployed in order to establish the sufficient convergence
conditions of the estimation error in terms of a set of
Linear Matrix Inequalities (LMIs) (Boyd et al., 1994)
which are solved using standard convex optimization
algorithms.
State estimation of decoupled multiple model has
been partially explored in a self-tuning control law
design perspective in (Gawthrop, 1995). Thanks to
the decoupling between the submodels, the observer
gains can be classically calculated under the assump-
tion that the submodel outputs are known. However,
in our case, it is assumed that this information is not
available. Therefore, this approach cannot be used
here.
The aim of this section is to investigate the state
estimation of a decoupled multiple model, using only
the measurable signals i.e. the input and the output of
the system (the outputs of the submodels are not avail-
able). It is important to notice that the design of the
observer must take into account the blending between
the outputs of the submodels in order to guarantee the
convergence of the estimation error.
4.1 Observer Structure
The proportional gain observer for the decoupled
multiple model is given by:
ˆx
i
(k+ 1) = A
i
ˆx
i
(k) + B
i
u(k) + K
i
(y(k) − ˆy(k)),
ˆy
i
(k) = C
i
ˆx
i
(k), (6)
ˆy(k) =
L
∑
i=1
µ
i
(k) ˆy
i
(k),
where ˆx
i
∈ R
n
i
is the state estimation for the i
th
sub-
model, y(k) the output of the multiple model, ˆy(k) the
output estimation and K
i
∈ R
n
i
×p
the gain of the i
th
observer. Equation (6) can be written in a compact
form using the partitioned matrices (5):
ˆx(k+ 1) = A
obs
(k) ˆx(k) +
˜
Bu(k) +
˜
Ky(k),
ˆy(k) =
˜
C(k) ˆx(k), (7)
where
˜
K = [
K
1
··· K
i
··· K
L
]
T
, (8)
A
obs
(k) =
˜
A−
˜
K
˜
C(k). (9)
Note that the matrix A
obs
(k) may be decomposed as
follows:
A
obs
(k) =
L
∑
i=1
µ
i
(k)Φ
i
, (10)
Φ
i
=
˜
A−
˜
K
˜
C
i
, (11)
where
˜
C
i
is the following partitioned block matrix:
˜
C
i
=
0 ... C
i
.. . 0
. (12)
The design of the observer consists in determining
the gain
˜
K such that the estimation error given by:
e(k) = x(k) − ˆx(k), (13)
converges asymptotically to zero for an arbitrary
blending between the submodel outputs.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
144

4.2 Estimation Error Convergence
Here, the second Lyapunov method is used to inves-
tigate the estimation error convergence by means of
a quadratic Lyapunov function. It is clear that other
Lyapunov functions can be considered (see section
4.4). The following Theorem gives a sufficient con-
dition for ensuring the estimation error convergence.
Theorem 1. Consider the decoupled multiple model
(4) and the observer (6). The asymptotic convergence
towards zero of the estimation error is guaranteed if
there exists a symmetric and positive definite matrix P
and a matrix G such that:
P
˜
A
T
P−
˜
C
T
i
G
T
P
˜
A− G
˜
C
i
P
> 0, i = 1...L, (14)
where the observer gain is deduced from
˜
K = P
−1
G.
Proof. Let us consider the following quadratic Lya-
punov function:
V(e(k)) = e
T
(k)Pe(k), P = P
T
andP > 0. (15)
The variation of the above function is given by:
∆V(e(k)) = V(e(k+ 1)) −V(e(k)), (16)
∆V(e(k)) must be negative in order to ensure its de-
crease and the asymptotic error convergence also.
Considering the dynamics of the estimation error
given by:
e(k+ 1) = A
obs
(k)e(k), (17)
and substituting (15) and (17) into (16), then
∆V(e(k)) becomes:
∆V(e(k)) = e
T
(k){A
T
obs
(k)PA
obs
(k) − P}e(k), (18)
that is a quadratic form in e(k). Therefore,
a necessary and sufficient condition for ensuring
∆V(e(k)) < 0 is:
A
T
obs
(k)PA
obs
(k) − P < 0, ∀k. (19)
By considering (10), the inequality (19) can be rewrit-
ten as:
L
∑
j=1
µ
j
(k)Φ
T
j
PP
−1
P
L
∑
i=1
µ
i
(k)Φ
i
− P < 0, (20)
Combining the Schur complement with property (3a)
of the weighting functions, it is possible to write:
L
∑
i=1
µ
i
(k)
P Φ
T
i
P
PΦ
i
P
> 0. (21)
The inequality (21) can be upper bounded using the
property (3b) of the weighting functions. Finally, a
sufficient condition that ensures the error convergence
is given by:
P Φ
T
i
P
PΦ
i
P
> 0 i = 1...L (22)
and substituting (11) for Φ
i
, we obtain:
P (
˜
A−
˜
K
˜
C
i
)
T
P
P(
˜
A−
˜
K
˜
C
i
) P
> 0, i = 1...L. (23)
These matrix inequalities are nonlinear in
˜
K and P.
Therefore, it is not possible to solve them directly us-
ing classical LMI tools. The following change of vari-
ables G = P
˜
K allows the linearisation of this problem
and ends the demonstration of Theorem 1.
4.3 Eigenvalue Placement
In order to enforce dynamic performances of the ob-
server (for example, the damping and the estimation
error decay rate) the eigenvalue placement of the ob-
server must be investigated. In (Chilali and Gahinet,
1996) a general characterization for eigenvalues clus-
tering in subregions of the complex plan in terms of
LMIs is proposed.
The eigenvalues of the matrix X are placed inside
the circle with radius R and centred at (q,0) in the z
plan if the following LMI is feasible:
−RP −qP+ XP
−qP+ (XP)
T
−RP
< 0, (24)
where P is a symmetric and positive definite matrix.
Let us notice that if R = 1 and q = 0 then we obtain the
stability condition for linear discrete-time systems.
In order to place the eigenvalues of the observer,
the LMIs of Theorem 1 are modified as follows.
Theorem 2. Consider the decoupled multiple model
(4) and the observer (6). The eigenvalues of the ob-
server are placed inside the circle with radius R and
centred at (q,0) if there exists a symmetric and posi-
tive definite matrix P and a matrix G such that:
−RP −qP+
˜
A
T
P−
˜
C
T
i
G
T
−qP+ P
˜
A− G
˜
C
i
−RP
< 0, (25)
for i = 1...L, where the observer gain is given by
˜
K = P
−1
G.
It is clear that this Theorem coincides with The-
orem 1 if R = 1 and q = 0. In order to avoid strong
oscillations of the estimation error, the real part of the
eigenvalues of the observer are placed in the positive
zone of the unit circle and their imaginary part must
be reduced. A judicious choice of the radius R and
the centre (q,0), for example q = 0.5 and R = 0.45,
allows an appropriate placement of the eigenvalues of
the observer.
STATE ESTIMATION OF NONLINEAR DISCRETE-TIME SYSTEMS BASED ON THE DECOUPLED MULTIPLE
MODEL APPROACH
145

4.4 Relaxed Convergence Conditions
The asymptotic convergence conditions of the estima-
tion error, presented in the previous section, depend
on the existence of the common matrix P which sat-
isfies a set of LMIs. In general, when the multiple
model has a large number of submodels, the matrix P
cannot be found.
In order to reduce the conservatism of the con-
ditions obtained with a quadratic Lyapunov func-
tion, new candidate Lyapunov functions called non-
quadratic functions have been proposed. A wide
number of published works show the efficient relax-
ation of the stability conditions provided by this class
of functions for a continuous time Takagi-Sugeno
multiple model (Jadbabaie, 1999; Rhee and Won,
2006) and also in the discrete time case (Guerra and
Vermeiren, 2004). The following Theorem gives a
sufficient condition for ensuring the estimation error
convergence using a nonquadratic function.
Theorem 3. Consider the decoupled multiple model
(4) and the observer (6). The asymptotic convergence
towards zero of the estimation error is guaranteed if
there exists symmetric and positive definite matrices
P
i
and P
j
and a some matrix M and G such that:
P
i
(M
˜
A− G
˜
C
i
)
T
M
˜
A− G
˜
C
i
M + M
T
− P
j
> 0 ∀i, j = 1...L, (26)
where the observer gain is deduced from
˜
K = M
−1
G.
Proof. The considered nonquadratic Lyapunov func-
tion is given by:
V(e(k)) = e
T
(k)
L
∑
i=1
µ
i
(k)P
i
e(k) = e
T
(k)P(k)e(k), (27)
where P
i
= P
T
i
and P
i
> 0. The convergence error
analysis is performed as in the previous case. A nec-
essary and sufficient condition in order to ensure the
error convergence is given by:
A
T
obs
(k)P(k + 1)A
obs
(k) − P(k) < 0. (28)
Introducing (10) and using the Schur complement, the
above inequality becomes:
L
∑
j=1
L
∑
i=1
µ
i
(k)µ
j
(k+ 1)
P
i
Φ
T
i
P
j
P
j
Φ
i
P
j
> 0. (29)
Using property (3b) of the weighting functions and
substituting (11) for Φ
i
, one obtains the following suf-
ficient condition that ensures the asymptotic conver-
gence of the estimation error:
P
i
(
˜
A−
˜
K
˜
C
i
)
T
P
j
P
j
(
˜
A−
˜
K
˜
C
i
) P
j
> 0, i, j = 1...L. (30)
Inequalities (30) are nonlinear matrix inequalities in
˜
K, P
i
and P
j
. In contrast to the quadratic case, there is
not variable change that allows the direct linearisation
of this problem. However, the results coming from
(De Oliveira et al., 1999) (Theorem 2) help to rewrite
the inequalities (30) as follows:
P
i
(M(
˜
A−
˜
K
˜
C
i
))
T
M(
˜
A−
˜
K
˜
C
i
) M + M
T
− P
j
> 0, i, j = 1...L,
where M is not constrained to be symmetric (M 6=
M
T
). After this transformation, the linearisation of
the above inequalities can be effectively yielded by
using the change of variables G = M
˜
K. Hence, the
proof of Theorem 3 is completed.
Notice that Theorem 1 is encompassed by Theo-
rem 3. Indeed, if one sets P
i
= P
j
= M = P then the
Theorem 3 coincides with the Theorem 1. Therefore,
the previous result is less conservative than the condi-
tion obtained with a conventional quadratic function.
5 EXAMPLE
Let us consider the state estimation of the decoupled
multiple model with L = 3 submodels. The numerical
matrices A
i
, B
i
and C
i
are:
A
1
=
0.8 0
0.4 0.1
, A
2
=
h
−0.3 −0.5 0.2
0.7 −0.8 0
−2 0.1 0.7
i
, A
3
=
−0.5 0.1
−0.6 −0.5
,
B
1
= [
0.2 −0.4
]
T
, B
2
= [
0.7 −0.5 0.3
]
T
, B
3
= [
−0.2 0
]
T
,
C
1
=
0.7 0
0.5 0.2
, C
2
=
0.5 0 0.8
0.7 0.2 0.1
, C
3
=
0.9 0.3
−0.6 0
.
Here, the decision variable ξ is the input signal u(k) ∈
[0,1]. The weighting functions are obtained from nor-
malised Gaussian function:
µ
i
(u(k)) = ω
i
(u(k))/
L
∑
j=1
ω
j
(ξ(k)), (31)
ω
i
(u(k)) = exp
−(u(k) −c
i
)
2
/σ
2
, (32)
with the standard deviation σ = 0.4 and the centre
c
i
= [0.1,0.5,0.9]. The eigenvalues of the matrix
˜
A are inside the unit circle, thus the multiple model
is stable. Using Theorem 3, we obtain the following
observer gain:
˜
K =
0.041 0.020 0.160 0.190 0.221 −0.090 −0.181
0.194 0.113 −0.299 −0.044 −0.701 0.172 0.268
T
.
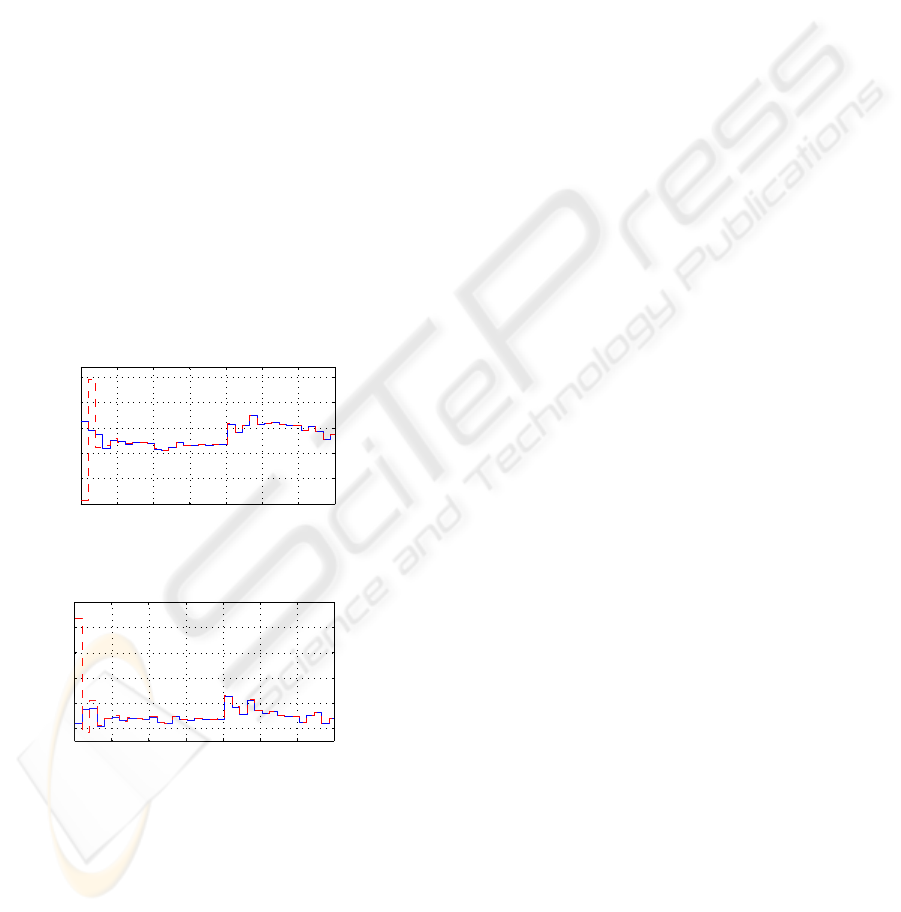
As can be seen in figures 1 and 2, the suggested ob-
server provides a good output estimation. The error
around the origin time is due to the different initial
conditions of the multiple model and the observer.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
146
6 CONCLUSION
A decoupled discrete time multiple observer has been
presented in order to proceed to the state estimation of
a class of nonlinear systems. The proposed observer
is an extension of the proportional observer used in
the linear observer theory.
Sufficient conditions that guarantee the asymp-
totic convergence of the estimation error are given in
terms of a set of LMIs using a quadratic Lyapunov
function. Less conservative conditions are also pro-
posed thanks to a nonquadratic Lyapunov function.
In order to illustrate the performances of the proposed
observer an academic example is presented.
There are interesting prospects in control and di-
agnosis of nonlinear systems using this class of mul-
tiple model and observer. In particular, this observer
class may be useful for setting up a diagnosis strategy
for example. This task can be done with a bank of the
proposed observers that produce a set of residual sig-
nals useful for sensor fault detection and isolation. In
future work, the proposed approach will be extended
to other observer classes as proportional integral ob-
server or unknown input observer.
0 5 10 15 20 25 30 35
−1.5
−1
−0.5
0
0.5
1
Figure 1: Output y
1
of the multiple model (solid line) and
its estimated (dashed line).
0 5 10 15 20 25 30 35
0
0.2
0.4
0.6
0.8
1
Figure 2: Output y
2
of the multiple model (solid line) and
its estimated (dashed line).
REFERENCES
Akhenak, A., Chadli, M., Ragot, J., and Maquin, D. (2004).
Estimation of state and unknown inputs of a nonlinear
system represented by a multiple model. In 11h IFAC
Symposium on Automation in Mineral and Metal pro-
cessing, Nancy, France.
Boyd, S., El Ghaoui, L., Feron, E., and Balakrishnan, V.
(1994). Linear Matrix Inequalities in System and Con-
trol Theory. Philadelphia, P.A., SIAM studies in ap-
plied mathematics edition.
Chadli, M., Maquin, D., and Ragot, J. (2003). Multiple
observers for discrete-time multiple models. In Safe-
process, pages 801–806, Washington, D.C., USA.
Chilali, M. and Gahinet, P. (1996). H-infinity design with
pole placement constraints: an LMI approach. IEEE
Transactions in Automatic and Control, 41(3):358–
367.
De Oliveira, M., Bernussou, J., and Geromel, J. (1999). A
new discrete-time robust stability condition. Systems
Control Letters,, 37(4):261–265.
Feng, G., Cao, S. G., Rees, N. W., and Chak, C. K. (1997).
Design of fuzzy control systems with guaranteed sta-
bility. Fuzzy Sets and Systems, 85(1):1–10.
Filev, D. (1991). Fuzzy modeling of complex sys-
tems. International Journal of Approximate Reason-
ing, 5(3):281–290.
Gasso, K., Mourot, G., and Ragot, J. (2001). Structure iden-
tification in multiple model representation: elimina-
tion and merging of local models. In 40th IEEE Con-
ference on Decision and Control, pages 2992–2997,
Orlando, USA.
Gatzke, E. P. and Doyle III, F. J. (1999). Multiple model ap-
proach for CSTR control. In 14 IFAC World Congress,
pages 343–348, Beijing, P. R. China.
Gawthrop, P. (1995). Continuous-time local state lo-
cal model networks. In IEEE Conference on Sys-
tems, Man & Cybernetics, pages 852–857, Vancouver,
Canada.
Gregorcic, G. and Lightbody, G. (2000). Control of highly
nonlinear processes using self-tuning control and mul-
tiple/local model approaches. In 2000 IEEE Interna-
tional Conference on Intelligent Engineering Systems,
INES 2000, pages 167–171.
Guerra, T. M. and Vermeiren, L. (2004). LMI-based re-
laxed nonquadratic stabilization conditions for nonlin-
ear systems in the Takagi-Sugeno’s form. Automatica,
40(5):823–829.
Jadbabaie, A. (1999). A reduction in conservatism in stabil-
ity and L2 gain analysis of Takagi-Sugeno fuzzy sys-
tems via linear matrix inequalites. In 14h IFAC World
Congress, pages 285–289, Beijing, P. R. China.
Johansen, T., Shorten, R., and Murray-Smith, R. (2000).
On the interpretation and identification of dynamic
Takagi-Sugeno fuzzy models. IEEE Trans. on Fuzzy
Systems, 8(3):297–313.
Murray-Smith, R. and Johansen, T. (1997). Multiple model
approaches to modelling and control. Taylor & Fran-
cis.
Palm, R. and Bergstern, P. (2000). Sliding mode observer
for a Takagi-Sugeno fuzzy system. In The Ninth IEEE
International Conference on Fuzzy Systems, volume 2,
pages 665–670, San Antonio.
STATE ESTIMATION OF NONLINEAR DISCRETE-TIME SYSTEMS BASED ON THE DECOUPLED MULTIPLE
MODEL APPROACH
147

Rhee, B. and Won, S. (2006). A new fuzzy Lyapunov func-
tion approach for a Takagi-Sugeno fuzzy control sys-
tem design. Fuzzy Sets and Systems, 157(9):1277–
1228.
Tanaka, K. and Sugeno, M. (1990). Stability analysis of
fuzzy systems using Lyapunov’s direct method. In
NAFIPS, pages 133–136, Toronto, Canada.
Venkat, A., Vijaysai, P., and Gudi, R. (2003). Identifica-
tion of complex nonlinear processes based on fuzzy
decomposition of the steady state space. Journal of
Process Control, 13(6):473–488.
ICINCO 2007 - International Conference on Informatics in Control, Automation and Robotics
148
