
Fourier Signature in Log-Polar Images
A. Gasperin, C. Ardito, E. Grisan and E. Menegatti
Intelligent Autonomous Systems Laboratory (IAS-Lab)
Department of Information Engineering
Via Gradenigo 6/b, 35131 Padova, Italy
Abstract. In image-based robot navigation, the robot localises itself by compar-
ing images taken at its current position with a set of reference images stored in
its memory. The problem is then reduced to find a suitable metric to compare im-
ages, and then to store and compare efficiently a set of images that grows quickly
as the environment widen. The coupling of omnidirectional image with Fourier-
signature has been previously proved to be a viable framework for image-based
localization task, both with regard to data reduction and to image comparison.
In this paper, we investigate the possibility of using a space variant camera, with
the photosensitive elements organised in a log polar layout, thus resembling the
organization of the primate retina. We show that an omnidirectional camera us-
ing this retinal camera, provides a further data compression and excellent image
comparison capability, even with very few components in the Fourier signature.
1 Introduction
A mobile robot that moves from place to place in a large scale environment needs to
know its position in the environment to successfully plan its path and its movements.
The general approach to this problem is to provide the robot with a detailed descrip-
tion of the environment (usually a geometrical map) and to use some kind of sensors
mounted on the robot to locate in its world representation. Unfortunately, the sensors
used by the robots are noisy, and they are easily misled by the complexity of the en-
vironment. Nevertheless, several works successfully addressed this solution using high
precision sensors like laser range scanners combined with very robust uncertainty man-
agement systems [13] [2]. Another solution, very popular in real-life robot applications,
is the management of the environment. If artificial landmarks, such as stripes or reflect-
ing dots, are added to the environment, the robot can use these objects, which are easy
to spot and locate, to calculate its position on a geometrical map. An example of a
successful application of this method is the work of Hu [6]. Unfortunately, these two
approaches are not always feasible. There are situations in which an exact map of the
environment is either unavailable or useless for example, in old or unexplored build-
ings or in environments in which the configuration of objects in the space changes fre-
quently. So, the robot needs to build its own representations of the world. This means
that in most cases a geometrical map contains more information than that needed by
the robot to move in the environment. Often, this adds unnecessary complexity to the
map building problem. In addition to the capability of reasoning about the environment
Gasperin A., Ardito C., Grisan E. and Menegatti E. (2007).
Fourier Signature in Log-Polar Images.
In Robot Vision, pages 87-96
DOI: 10.5220/0002070100870096
Copyright
c
SciTePress

topology and geometry, humans show a capability for recalling memorised scenes that
help themselves to navigate. This implies that humans have a sort of visual memory
that can help them locate themselves in a large environment. There is also experimental
evidence to suggest that very simple animals like bees and ants use visual memory to
move in very large environments [3]. From these considerations, a new approach to the
navigation and localization problem developed, namely, image-based navigation. The
robotic agent is provided with a set of views of the environment taken at various loca-
tions. These locations are called reference locations because the robot will refer to them
to locate itself in the environment. The corresponding images are called reference im-
ages. When the robot moves in the environment, it can compare the current view with
the reference images stored in its visual memory. When the robot finds which one of
the reference images is more similar to the current view, it can infer its position in the
environment. If the reference positions are organised in a metrical map, an approximate
geometrical localization can be derived. With this technique, the problem of finding the
position of the robot in the environment is reduced to the problem of finding the best
match for the current image among the reference images. The problem now is how to
store and to compare the reference images, which for a wide environment can be a large
number. In order to store and match a large number of images efficiently, it has been
shown in [9] the transformation of omnidirectional views into a compact representa-
tion by expanding it into its Fourier series. The agent memorises each view by storing
the Fourier coefficients of the low frequency components. This drastically reduces the
amount of memory required to store a view at a reference location. Matching the current
view against the visual memory is computationally inexpensive with this approach.
We show that a further reduction in memory requirements and computations can be
met by using log-polar images, obtained by a retina-like sensor, without any loss in the
discriminatory power of the methods.
2 Materials
2.1 Omnidirectional Retinal Sensor
The retina-like sensor used in this work is the Giotto camera developed by Lira-Lab at
the University of Genova [11] [12] and by the Unitek Consortium [4]. It is built using
the 35µm CMOS technology, and arranging the photosensitive elements in a log-polar
geometry. A constant number of elements is placed on concentric rings, so that the size
of these elements necessarily decreases from the periphery toward the center. This kind
of geometric arrangement has a singularity in the origin, where the element dimension
would shrink to zero. Since this dimension is constrained by the building technology
used, there is a ring from which no dimension decrement is possible for accomodat-
ing a constant number sensitive elements. Hence, the area inside this limiting ring does
not show a log-polar geometry in the arrangement of the elements, but is nevertheless
designed to preserve the polar structure of the sensor and at the same time tessellate
the area with pixels of the same size. This internal region will be called the fovea of
the sensor for its analogy with the fovea in the animal retina, whereas the region with
constant number of pixels per ring will be called periphery.
The periphery is composed by N
per
= 110 rings with M = 252 pixels each, and the
88
Fig.1. The central part of the electronic layout of the retinal sensor (from [4]).
fovea is composed by N
f ov
= 42 rings (see Fig. 1). This lead to a log-polar image hav-
ing size of MxN = 252x152, where N = (N
per
+ N
f ov
), and the image is obtained
from a sensor with 38.304 photosensitive elements. It is claimed in [4] that given its
resolution, the log polar sensor yields an image equivalent to a 1090x1090 image ac-
quired with a usual CCD: a sample image acquired with this camera is shown in Fig. 2,
together with its cartesianig:retina remapping in Fig. 3
Fig.2. A sample 252x152 image acquired
with the retina-like camera.
Fig.3. The sample image of Fig. 2 trans-
formed in a 1090x1090 cartesian image.
To obtain the omnidirectional sensor, the retina-like camera is coupled with an hy-
perbolic mirror with a black needle at the apex of the mirror to avoid internal reflections
89

on the glass cylinder [7]: the sensor can be seen in Fig. 4(a). A single omnidirectional
image gives a 360
o
view of the environment, as can be seen in Fig. 4(b).
(a) (b)
Fig.4. (a) The omnidirectional sensor composed by the retina-like camera and the hyperbolic
mirror. (b) A sample image acquired with the omnidirectional retinal sensor.
3 Methods
3.1 Log-Polar Omnidirectional Image
The pixel coordinates of the output image of the retinal sensor are polar coordinates
(ρ, ϑ), that are related to the usual cartesian coordinates (x, y) via:
ρ = log
p
x
2
+ y
2
ϑ = arctan
y
x
(1)
There are two main issues to be considered while dealing with log-polar images. The
first is that there is a singularity in the transformation near the origin, where the pixel
dimension tend to zero. The transformation can thus be considered exact only in the re-
gion outside the fovea, whereas inside the fovea the mapping depends on the particular
arrangement of the retinal sensor.
The second point is the consideration that given the sampling in polar coordinates in-
duced by the sensor, moving from the center toward the periphery of the image, the
mapping is not bijective from (ρ
i
, ϑ
i
) → (x
i
, y
i
), but rather one point in the log polar
image correspond to a sector of annular ring:
(ρ
i
, ϑ
i
) → {(x, y)|ρ ∈ [ρ
i
, ρ
i+1
[ ∩ ϑ ∈ [ϑ
i
, ϑ
i+1
[} (2)
This means that from the center of the image toward its outer boundary, the resolution
decreases, as a pixel in the log-polar image gather information from a bigger area than
90

a pixel, e.g., in the fovea.
An interesting property of the retinal sensor appears when it is coupled with an hyper-
bolic mirror,so to provide an omnidirectional sensor.In fact the space-variant resolution
of the sensor, if matched with the hyperbolic projection provide an omnidirectional im-
age of nearly constant resolution. Moreover,the image acquired by this omnidirectional
sensor is already in the form of a panoramic cylinder, without need of further transfor-
mations [12,10].
3.2 Fourier Signature
In image-based navigation the main problem is the storage of reference images and
the comparison of these images with those acquired during the localization. In [9] was
shown the effectiveness of using a small number of Fourier coefficients to characterize
an image: that method both reduce drastically the dimension of the information to be
stored and proved to be enough to discriminate different images, without the need of
image alignment as in [1] [5] [8].
The Fourier signature is computed in two steps. First, we calculate the 1-D Fourier
transform of every line of the log-polar image and we store in a matrix the Fourier
coefficients line by line. Then, we keep only a subset of the Fourier coefficients, those
corresponding to the lower spatial frequencies, as signature for the image.
To fully exploit the further dimensionality reduction imposed by the retina-like sensor,
we have to recall that in the fovea the effectivephysical pixels (and therefore the amount
of information) is 1 in the center, that is mapped in first line of the log-polar image, 4
in the second innermost ring, mapped in the second line, and so on until the number
of pixels in the ring match that of the periphery, where the amount of pixels per ring is
constant. A number of physical pixels smaller than the number of image pixels induces
a smaller band on the signal than it would be possible given the image dimension.
This leads to the consideration that in the foveal region we need to retain less Fourier
coefficients than in the periphery to achieve a storage efficiency without loosing any
information. The choice is therefore to decrease linearly the number of coefficients
used to build the signature: from the k
max
per line in the periphery (rows N
f ov
+ 1 to
N in the log-polar image), to the 1 coefficient of the first line of the image. Hence for
the row y:
k(y) =
(
⌈
k
max
−1
N
fov
−1
· y +
k
max
−N
fov
k
max
−1
⌉ if y ≤ N
f ov
k
max
if y > N
f ov
(3)
with ⌈x⌉ meaning the ceiling of x.
3.3 Dissimilarity Measure
Given an image I, and the discrete set of its Fourier coefficients for the line y, a
y,k
,
with y = 1, . . . , N, we can define the Fourier signature as the vector F containing the
juxtaposition of all Fourier coefficients of the signature for each line:
F(I) =
a
1,1
, . . . , a
1,k(1)
, . . . , a
N,1
, . . . , a
N,k(N)
(4)
91

A distance between two images I
i
and I
j
can be evaluated as the L
1
norm between the
two vectors of their Fourier signature:
d(I
i
, I
j
) = |F(I
i
) − F(I
i
)|
1
(5)
When a database of images is available, and a new image have to be compared with
those in the database to find the best match, is often more intuitive to use a measure of
relative distance of the image under examination from one in the database, given all the
images in the database:
p(I
i
, I
j
) = 1 −
d(I
i
, I
j
)
max
i,j
(d(I
i
, I
j
))
(6)
This is a normalized distance in the database, assuming values in the interval [0, 1], and
can therefore be viewed as a probability a posteriori of an image I
i
to be equal to image
I
j
, with j = 1, . . . , N, and N the number of images in the database.
4 Results and Discussion
To test the proposed measure, an image database was built by acquiring a frame from
different positions in an indoor environment, using the retinal omnidirectional camera
described previously. The acquisition sites were 15 locations 20cm apart.
First of all, we made experimentations to evaluate which is the minimum number of
Fourier coefficients necessary to construct a Fourier signature that retains all and only
the necessary information. Hence, we calculated the similarity of each input image
against all the reference image of the dataset varying the number of coefficients per row
(k
max
) of the Fourier signature. Since the Nyquist frequency of each row is f
Ny
=
N
2
,
the maximum number of coefficients of the DFT which yield effective information is
N
2
. Therefore, we made k
max
∈ K = [1, . . . ,
N
2
].
For each k
max
∈ K we first evaluated the similarity measure Eq. (6) of each image
in the reference database from every other image in the reference database. By this
mean, we show that Eq. (6) is an effective measure to distinguish different images, and
can therefore be used to provide a good localization performance in autonomous robot
navigation tasks. In Fig. 7 we show three successive sample images (relative distance
equal to 15cm) from the reference database, and the similarity value of an input image
taken at a location corresponding to the second reference image. The similarity value
yields a correct match between input and reference.
In Fig. 5 and Fig. 6, it is shown the values of the similarity value for different values
of k
max
of an image in the reference database with every other image. In both figures,
the similarity peak corresponds to the correct image, and the similarity values decrease
around the peak, the higher k
max
, the sharper the decrease.
The choice of k
max
influences the trade off between dissimilarity accuracy and image
storage efficiency. A good measure of the accuracy of the proposed measure is the mini-
mum differencebetween 1−d(I
i
, I
j
) for i 6= j. This is equivalent to evaluate a classifier
92

2 4 6 8 10 12 14
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Images
Similarity Value
1 Fourier Coefficient per Row
63 Fourier Coefficients per Row
126 Fourier Coefficients per Row
Fig.5. Similarity measure p(I
5
, I
j
) for j = 1, . . . , N, for k
max
= 1, 63, 126. It is clear that the
correct image always yields a similarity measure of 1, whereas the decreasing in the similarity is
sharper for high values of k
max
.
2 4 6 8 10 12 14
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Images
Similarity Value
1 Fourier Coefficient per Row
63 Fourier Coefficient per Row
126 Fourier Coefficients per Row
Fig.6. Similarity measure p(I
10
, I
j
) for j = 1, . . . , N , for k
max
= 1, 63, 126. It is clear that the
correct image always yields a similarity measure of 1, whereas the decreasing in the similarity is
sharper for high values of k
max
.
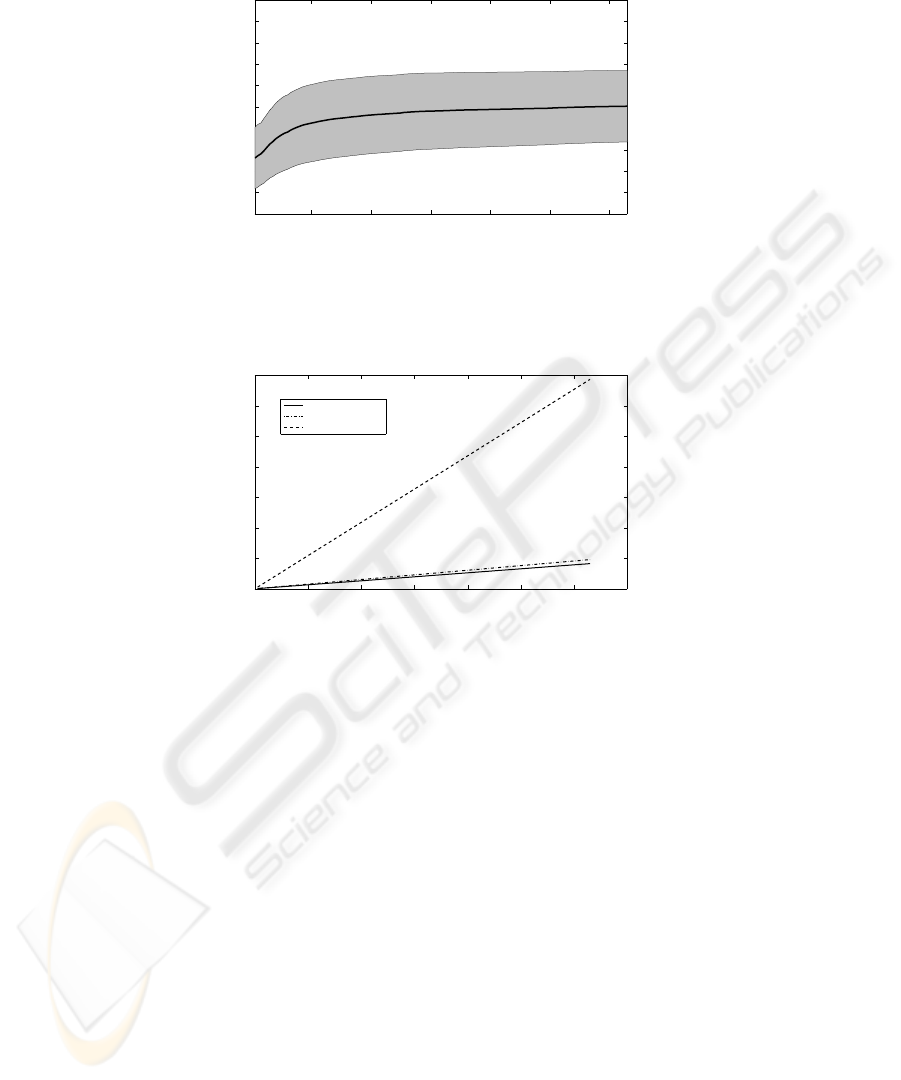
margin, in the separation between two different images. In Fig. 8, we show that after a
monotonic increase in this margin whith the number of coefficients, it reaches a kind of
plateau after k
max
≃ 20.
The storage efficiency achieved is clear when comparing the number of Fourier
coefficients needed to form the Fourier signature of a log-polar image with the number
of the equivalent cartesian image, which has dimension 1090x1090 pixels. In Fig. 9
we show for different k
m
ax the dimension of the Fourier signature for the equivalent
cartesian image, for the log-polar image with k
max
coefficients per row, and for the log-
polar image with k(y) coefficients per row, meaning that we have a reduced number of
coefficients in the foveal rings. It is well apparent the storage reduction that can be
achieved using a retina-like sensor.
93

(a) Reference Image 1 (b) Reference Image 2
(c) Reference Image 3 (d) Input Image
Fig.7. Three reference image taken 15 cm apart, to be confronted with an input image acquired
at location (b). With k
max
= 10, the similarity value of the input image with image (a) is 0.59,
with (b) is 0.96, and with (c) is 0.54: the correct match has the highest similarity value.
5 Conclusions
In this paper we show that retinal omnidirectional images can be successfully used
to localize an autonomous robot with the image-based navigation approach. Within
this approach, the direct comparison of images is not robust, is too computationally
cumbersome, and the storage of the whole images requires an excessive memory space.
Representing the images with their Fourier signature has been proved a viable way to
overcome these problems. In this paper, we showed that coupling this technique with
log-polar sensor yields a further dimensionality reduction with sufficient accuracy.
The reduction is achieved by exploiting the different bandwidth of each ring of the
retina-like sensor with respect to the constant bandwidth of a cartesian sensor, where
each row contains the same number of photosensitive element. This allows to keep a
decreasing number of Fourier coefficients in the signature, moving from the periphery
toward the center of the sensor.
Despite the storage requirement reduction, we show that using a simple L
1
norm on
difference of signature vectors have an excellent discriminatory power in distinguishing
images taken at different sites.
94
20 40 60 80 100 120
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Number of Coefficients per Row in the Fourier Signature
Minimum Dissimilarity Value
Fig.8. Minimum difference in the proposed similarity measure p(I
i
, I
j
) for every different im-
age in the database, and for k
max
= 1, . . . , 126. The solid line represent the mean minimum
difference µ, and the gray area represent the variability of this value µ ± σ.
0 20 40 60 80 100 120 140
0
2
4
6
8
10
12
14
x 10
4
k
max
Number of elements in the Fourier Signature
Foveal Coefficients Reduction
Equal k
max
for each Row
Equivalent Cartesian Image
Fig.9. Total number of coefficients needed to form the proposed Fourier Signature, with respect
to k
max
.
Acknowledgements
We would like to thank Prof. G. Sandini and coworkers for having kindly provided the
retinal camera, of which only few prototypes exist.
This research has been partially supported by the Italian Ministry for Education and
Research (MIUR) and by the University of Padova (Italy).
References
1. H. A. ans N. Iwasa, N. Yokoya, and H. Takemura. Memory-based self-localisation using
omnidirectional images. In Proceedings of the 14th International Conference on Pattern
Recognition, volume 1, pages 1799–1803, 1998.
2. W. Burgard, D. Fox, M. Moors, R. Simmons, and S. Thrun. Collaborative multi-robot explo-
ration. In Proceedings of the IEEE International Conference on Robotics and Automation
(ICRA), 2000.
95

3. T. Collett, E. Dillmann, A. Giger, and R. Wehner. Visual landmarks and route following in
desert ants. Journal of Comparative Physiology A, 170:435–442, 1992.
4. Consorzio Unitek. Giotto : retina-like camera.
5. J. Gaspar, N. Winters, and J. Santos-Victor. Vision-based navigation and environmental rep-
resentations with an omnidirectional camera. IEEE Transactions on robotics and automa-
tion, 16(6):890–898, December 2000.
6. H. Hu and D. Gu. Landmark based localisation of industrial mobile robots. International
Journal of Industrial Robot, 27(6):458–467, November 2000.
7. H. Ishiguro. Development of low-cost compact omnidirectional vision. In R. Benosman and
S. B. Kang, editors, Panoramic Vision,, chapter 3. Springer, 2001.
8. B. J. A. Kroese, N. Vlassis, R. Bunschoten, and Y. Motomura. A probabilistic model for
appearance-based robot localization. Image and Vision Computing, 19(6):381–391, April
2001.
9. E. Menegatti, T. Maeda, and H. Ishiguro. Image-based memory for robot navigation using
properties of the omnidirectional images. Robotics and Autonomous Systems, 47(4):251–
267, July 2004.
10. T. Pajdla and H. Roth. Panoramic imaging with SVAVISCA camera - simulations and real-
ity. Ctu-cmp-2000-16, Center for machine perception - Czech Technical University, October
2000.
11. G. Sandini and G. Metta. Retina-like sensors: motivations, technology and applications.
2002.
12. G. Sandini, J. Santos-Victor, T. Pajdla, and F. Berton. OMNIVIEWS: direct omnidirectional
imaging based on a retina-like sensor. In Proceedings of IEEE Sensors 2002, June 12-14
2002.
13. S. Thrun, M. Beetz, M. Bennwitz, W. Burgard, A. B. Cremers, F. D. Fox, D. Haehnel,
C. Rosenberg, N. Roy, J. Schulte, and D. Schulz. Probabilistic algorithms and the interactive
museum tour-guide robot Minerva. International Journal of Robotics Research, 19:972–999,
2000.
96
