A TEXTURE-BASED METRIC EXTENSION FOR

SIMPLIFICATION METHODS

Carlos González, Pascual Castelló and Miguel Chover

Departmento de lenguajes y sistemas informáticos, Universitat Jaume I, Castellón, Spain

Keywords: Simplification methods, texture, error metric, edge collapse.

Abstract: We present an extension of the error metrics used in the simplification methods based on edge collapse

operations, which takes into account texture information. Many simplification methods are just based on the

geometry of the models, without considering texture information. As a result, the simplified models present

highly distorted textures. The metric presented here avoids the early collapse of edges that collide with non-

uniform regions of the texture. Detection of these regions is performed by an edge detector method based on

Canny. To test the new error metric, a geometric simplification method of our own based on edge collapses

was used. It can be observed that simplified models that are generated with this new metric present more

realistic results than before. This metric modifies the order of the edge collapses and is very useful for

multiresolution models. The computational cost of this metric is negligible in comparison to the

simplification time.

1 INTRODUCTION

Simplification methods were a great step forward in

interactive applications. These methods allow to

avoid storing and processing all the geometry of the

objects in the scene by simplifying them to produce

other objects with less geometry. This reduces the

load on the GPU. These methods attempt to produce

realistic simplified objects, with a similar

appearance to the original one.

Many simplification methods are based solely on

the geometry of the objects and attempt to achieve

good geometric results in the simplified object by,

for example, criteria based on the coplanarity of the

polygons. But in recent years, methods based on the

user’s point of view have been developed. These

methods try to generate not only good geometric

results, but also realistic results for the viewer by

removing, for example, parts of the object that are

not visible to the user. These methods usually work

by rendering the object from several points of view,

that is, by situating the camera at more than one

point around the object. Generally, this distribution

of the cameras is uniform.

But not only final geometry is important in the

output objects. Models usually have additional

attributes to their geometry. Interactive applications,

like games or CAD programs, need to present the

simplified models with a good appearance. These

applications must therefore present well-textured

models in the scene, because textures play an

important role in this kind of application.

There are not many simplification methods that

take texture information into account in the error

metric. As a result, texture is not considered when

calculating the order in which the edges are

collapsed.

One solution to this problem is presented in this

paper. Our work is valid for any simplification

method based on edge collapses.

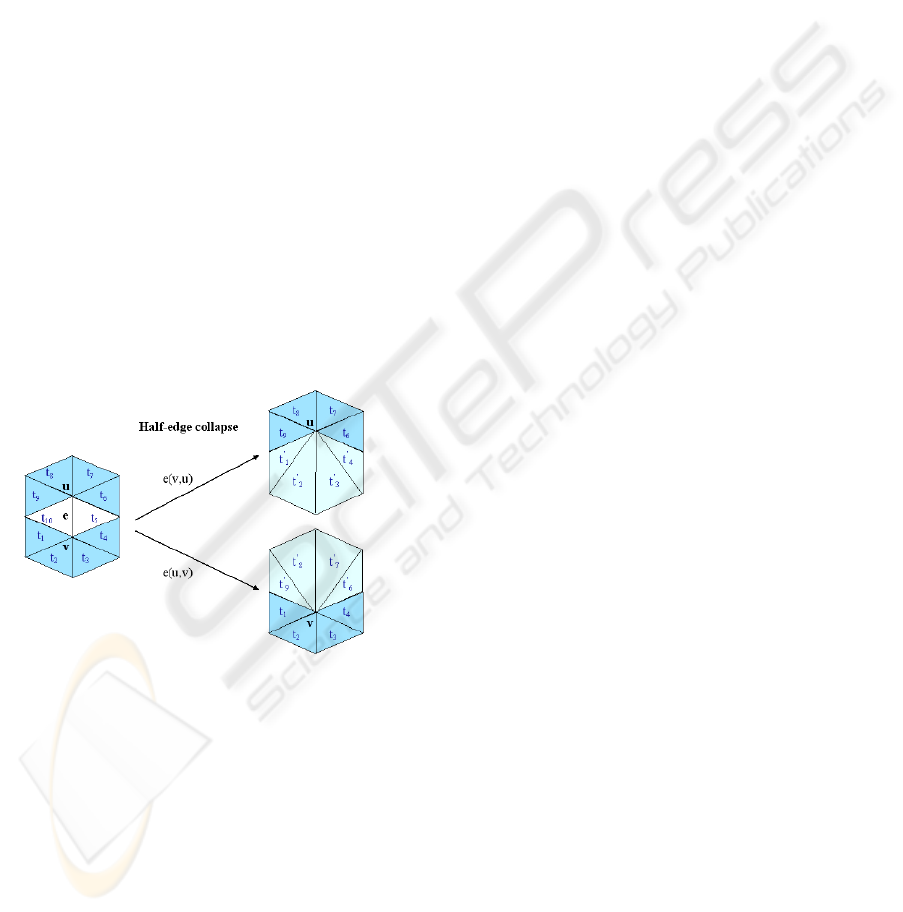
An edge collapse is a simplification operation

that removes edges by merging the vertices of the

edges. The final vertex can be placed at one of the

original vertices (half-edge collapse) or can be

moved to other spatial coordinates. Figure 1 shows

an example of a half-edge collapse operation.

We have developed an extension to the error

metric of any simplification method based on edge

collapses. The error metric extension presented here

is based on the information given by the texture

image. It attempts to distinguish the borders in the

texture and then uses this information to modify the

order of the collapses.

This error metric extension was tested with our

own geometric simplification method based on edge

collapse operations that make use of quadrics. This

González C., Castelló P. and Chover M. (2007).

A TEXTURE-BASED METRIC EXTENSION FOR SIMPLIFICATION METHODS.

In Proceedings of the Second International Conference on Computer Graphics Theory and Applications - GM/R, pages 69-76

DOI: 10.5220/0002081000690076

 SciTePress

method did not originally take into account textured

models. Thus, simplifying a model usually produced

an important amount of distortion in the texture. In

an attempt to improve these results, we extended the

method with the error metric presented in this paper

in order to preserve the textures. This metric

produces a later simplification of the regions of the

model that contain abrupt changes in the texture.

This extension is very useful for the generation

of simplification sequences in multiresolution

models, commonly used in games. Multiresolution

models can be rendered in the scene at different

levels of detail, depending on various factors such as

the distance from the object to the viewer, the

relative importance of the object in the scene, etc.

Moreover, this method does not have to store new

texture coordinates at each step of simplification.

Methods that recalculate the texture coordinates,

however, do have to store the new values for each

step, needing more memory for these values.

The rest of this paper is structured as follows. In

Chapter 2 we describe the background to this

research. In Chapter 3 we define the new metric and

a justification of this metric is exposed. Chapter 4

shows some results and in Chapter 5 we discuss the

conclusions.

Figure 1: The half-edge collapse operation. In this

example the edge e is collapsed into vertex u (see e(v, u)),

but is also collapsed into v (see e(u, v)). Triangles t10 and

t5 are removed.

2 PREVIOUS WORK

Cohen et al. (Cohen, Olano & Manocha, 1998)

presented a method that parameterises the model in

order to obtain the texels, obtaining some patches of

the surface. Texture deviation metric is used to

calculate the cost of the pairs. At each simplification

step this metric is calculated for the modified faces.

It also preserves the boundaries.

Garland and Heckbert (Garland & Herbert,

1998) improved their method (Garland & Herbert,

1997) by extending the quadrics, taking into account

the properties of the model. It also preserves the

boundaries, a high collapse cost being assigned to

these edges.

Hoppe (Hoppe, 1999) introduced a new quadric

metric for simplifying meshes while taking attributes

into consideration.

Lindstrom and Turk (Lindstrom & Turk, 2000)

introduced a pure image-based metric. This metric

was used in their image-driven simplification

method. The main advantage of this image metric is

that it allows the texture attributes to be taken into

account, while also measuring the error made in

edge collapse.

Luebke and Hallen (Luebke & Hallen, 2001)

presented a method for performing a view-

dependent polygonal simplification using perceptual

metrics. These metrics derive from a measure of

low-level perceptibility of visual stimuli in humans.

Later Williams et al. (Williams, Luebke, Cohen,

Kelley & Schubert, 2003) extended this work for lit

and textured meshes.

Sander et al. presented a method (Sander et al,

2001) that extended the work introduced in (Hoppe,

1996). This method subdivides the surface into

patches, on the grounds of its coplanarity. It then

generates a parameterisation by minimising the

stretch deviation. It calculates an adequate size for

each object in the texture domain and simplifies the

mesh by minimising the texture deviation (Cohen,

Olano & Manocha, 1998) and preserving the

boundaries. Finally, it optimises the parameterisation

with a different objective function and regroups all

the patches again.

Zhang et al. (Zhang & Turk, 2002) proposed a

new algorithm that takes visibility into account.

Their approach defined a visibility function between

the surfaces of a model and a surrounding sphere of

cameras. The number of cameras increases both

accuracy and calculation time. They used up to 258

cameras. In order to guide the simplification process,

they combined their visibility measure with the

quadric measure introduced by Garland et al.

(Garland & Herbert, 1997).

Lee et al. (Lee, Varshney & Jacobs, 2005)

introduced the idea of mesh saliency as a measure of

regional importance for graphics meshes. This

measure was incorporated into mesh simplification.

Basically, their approach consists in generating a

saliency map and then simplifying by using this map

in the QSlim algorithm as in (Zhang & Turk, 2002).

The new edge collapse cost is that of the quadric

multiplied by the saliency of this edge.

Garland and Zhou (Garland & Zhou, 2005)

presented a method for simplifying simplicial

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications

complexes of any type embedded in Euclidean

spaces of any dimension.

Both the geometry of the object and also the

texture frequencies were considered in (Xu, Sun &

Xu, 2005). To make the method more precise, pixels

are subdivided into subpixels.

The method presented in (Chen & Chuang,

2006) recalculates a new texture for each

simplification step, an indexing map being used to

avoid loss of precision.

3 ERROR METRIC EXTENSION

FOR TEXTURED MODELS

It is very important to use a simplification that

produces well-textured simplified objects, because

of the visual importance of texture.

There are many simplification methods for tri-

dimensional models, but only a few of them consider

the texture information in its error metric (Garland

& Herbert, 1998) (Hoppe, 1999) (Xu, Sun & Xu,

2005). Therefore, the methods which do not consider

texture information usually present simplified

models with distorted textures. The methods which

do consider this information normally use a specific

metric that is only valid for them.

Our error metric extension is very useful for

multiresolution methods because it does not need to

store new values for each level of detail. We

distinguish between our technique and the methods

that recalculate the values of the texture coordinates

at each level of detail.

In this paper we present a solution to this

problem. Thus, the error metric extension presented

here provides a way to consider the texture

information in methods in which no texture

information is taken into account in the metric.

3.1 Error Metric Extension

We have developed a new texture-based error metric

extension for simplification algorithms which use

the edge collapse operation. It is based on the shape

of the texture, so that the simplified model has a

more realistic appearance when the texture is

applied. Simplification methods which use edge

collapses assign a cost to each edge that determines

the order of the collapses. Depending on the borders

of the texture, we modify the cost of each edge in

order to penalise those edges that intersect these

borders. We will now go on to explain the steps

performed in order to achieve this.

First of all we detect the borders of the texture.

This is performed by an edge detector method based

on Canny (Canny, 1983) (Canny, 1986). This edge

detector works in a multi-stage process. First, a

Gaussian convolution is applied in order to smooth

the texture. Then, regions of the texture with high

first spatial derivatives are highlighted by applying a

simple 2D first derivative operator. Edges give rise

to ridges in the gradient magnitude image. Non-

maximal-suppression is then applied, that is, all

pixels that are not actually on the ridge top are set to

zero. These pixels would be drawn as a thin line in

the output. Two thresholds are used to apply

hysteresis so as to allow the continuity of noisy

edges.

The algorithm has various parameters which

affect the quantity and thickness of output borders.

These parameters are:

• The size of the Gaussian filter: depending on

how much the texture is smoothed by the Gaussian

convolution, less clear lines would be marked as

borders or not.

• Thresholds: the low and high thresholds would

give the algorithm what we think is relevant

information and withhold that which we believe is

not significant.

Once edge detection has been performed, the

result is an image with these borders. The values

(white or black) of each pixel in this image are

stored in a matrix. We now have the shape of the

borders in a data structure and we can work with

them.

If we applied this image to the 3D model, we

could see which edges intersect with borders (see

Figure 2). So, if an edge that intersects any of these

borders is collapsed, a great distortion in the texture

would be obtained. Therefore, these edges must have

a high cost of collapse.

We have to know which edges cross any

particular border. In order to achieve this, we use the

texels of each edge of the model. As a result, we

now know how each edge is located in the texture.

With a few simple 2D operations we can determine

whether this edge rendered in the texture crosses a

border. Let E be the set of these affected edges.

Figure 2 shows the Sphere model textured. In this

model the edges that have a part in a black region

and another part in a white region would pertain to

We store all the active edges in a heap, where

each edge has an associated cost. Therefore, edges

with a lower cost will be collapsed first. We then

modify the previous costs of the edges that pertain to

E to be collapsed later (Figure 3).

A TEXTURE-BASED METRIC EXTENSION FOR SIMPLIFICATION METHODS

The relative area of a region of the model is the

area of this region divided into the sum of the areas

of all the triangles of the model. The previous cost of

each edge is added to the relative area of the

triangles that contain the edge that we are analysing.

Hence, we define the total area of the model as

the sum of the areas of all the triangles in the model

(1). Thus, for one specific edge the additional cost

will be the sum of the areas of the triangles which

contain this edge divided by the total area of the

model (2). The area of each triangle therefore plays

an important role in the order of the edge collapses,

because this factor causes triangles with lower areas

to be removed before triangles with similar previous

costs and higher areas (if the model is manifold, in

an edge collapse one or two triangles are removed).

Therefore, the cost for each edge e of E (c

) is

performed as follows:

∑

(1)

n being the number of triangles in the model and

the actual area of the triangle i.

∑

(2)

t being the number of triangles the edge contains

and c

is the previous cost of the edge.

Figure 2: Sphere model.

Function getE(Texture, Model)

Begin

E = Ø

M = EdgeDetection(Texture)

For (each e of the Model)

If e collides with a border of M

then

Insert(e, E)

End If

Return E

End

Function computeTextureError(e, E)

Begin

If (e Є E) then

t = getTriangles(e)

Ct = relativeArea(t)

Else

Ct = 0

End If

Return Ct

End

Function computeEdgeCost(e, E)

Begin

Ce = computeEdgeCollapseError(e)

Ct = computeTextureError(e, E)

Return Ce+Ct

End

Figure 3: Pseudo-code for computing the cost of an edge.

Function getE(Texture, Model) returns the set of the edges

that intersect with any border of the texture. It is called at

the beginning of the process. The cost of each edge is

given by the function computeEdgeCost(e, E).

ComputeEdgeCollapseError returns the cost of collapsing

the edge e without considering texture information.

3.2 Justification of the Metric

The method is based on texture information and it is

clear which edges have to be penalised, but we have

to know how to change their collapse cost. We have

chosen the relative area of the triangles that contain

the collapsed edge as error extension, because the

greater the area of a triangle is, the more noticeable

its removal will be in the simplified object.

Another error metric extension that we

considered was the relative area of these triangles in

the texture domain because in this metric we are

taking into account the texture information, but the

texture coordinates of an object may not be

uniformly distributed. Small triangles in the 3D

space may therefore be parameterised with a large

triangle in the texture domain.

An example is shown in Figure 4, where the eye

of the Ninja model is almost as large as the other

parts of the body. If the area of the triangles in the

texture domain were used as the error metric the

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications

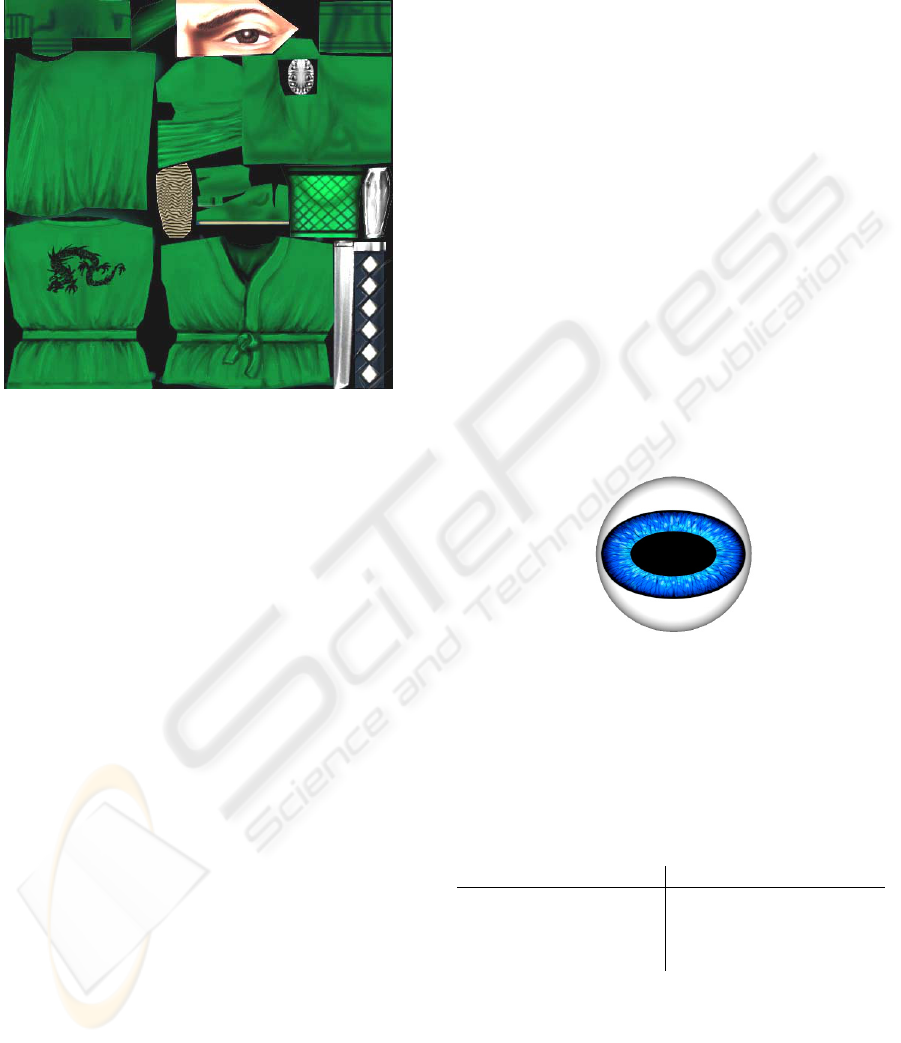
edges that contain the eyes would have a high

collapse cost. But the eyes are relatively small with

respect to other parts of the object when it is

rendered.

Figure 4: Texture of the Ninja Model.

4 RESULTS

Several models have been tested with the new error

metric and it can be observed that the texture in the

simplified models is more accurate to the original

models than in the simplified models without

applying our error metric.

The number of edges in the simplified models

remains unaltered, but the order of the simplification

of these edges was different. Now the edges that

collide in the texture domain with any border

obtained by the edge detector method have a higher

error cost. Thus, those parts of the model that have

fewer edges colliding with borders are more

simplified than before.

The border detection process is performed as a

pre-process. The border detection time depends on

the resolution of the texture and is a very fast

process. Moreover, the computational cost achieved

by this metric at each simplification step is

negligible compared with the simplification time.

The models were simplified by our own

geometric simplification method based on edge

collapse operations. We have tested several

parameters for the edge detector method and we

have chosen those that return what we think are

relevant borders. But if other values were given to

these parameters we would obtain more or fewer

borders of the texture and, consequently, more or

fewer edges that have to be reordered in the collapse

order.

Below, some simplified models are depicted.

Figure 5 shows the original Eye model. In Figure 6

the texture of this model and the borders of this

texture can be seen. Figures 7 and 8 show the

difference between applying and not applying the

metric in the Eye model. Three levels of

simplification are given (75%, 50% and 25%). These

percentages represent the number of edges

untouched. Figure 9 shows the texture of the Ninja

model and its borders detected by the edge detector

method. Figures 10 and 11 show a 50%

simplification of this model without applying the

new metric and applying it. First the original model

is shown (left), then the simplified model without

applying the metric (centre) and finally the

simplified model applying the metric (right). In

Figure 12 the texture of the Robot model and its

borders are shown. Figures 13 and 14 show the

difference between applying the metric with the

Robot model and not applying it in a simplification

at 50%. Figure 15 shows the texture of the

Toonturtle model and the borders that are obtained.

Figures 16 and 17 show a simplification at 25% of

the geometry of the Toonturtle model without

applying the new metric and then applying it. Table

1 shows the number of polygons in each of these

models.

Table 1: Number of polygons in each model.

Model Number of polygons

Eye 5,400

Ninja 1,008

Robot 308

Toonturtle 640

Figure 5: The original Eye model.

A TEXTURE-BASED METRIC EXTENSION FOR SIMPLIFICATION METHODS

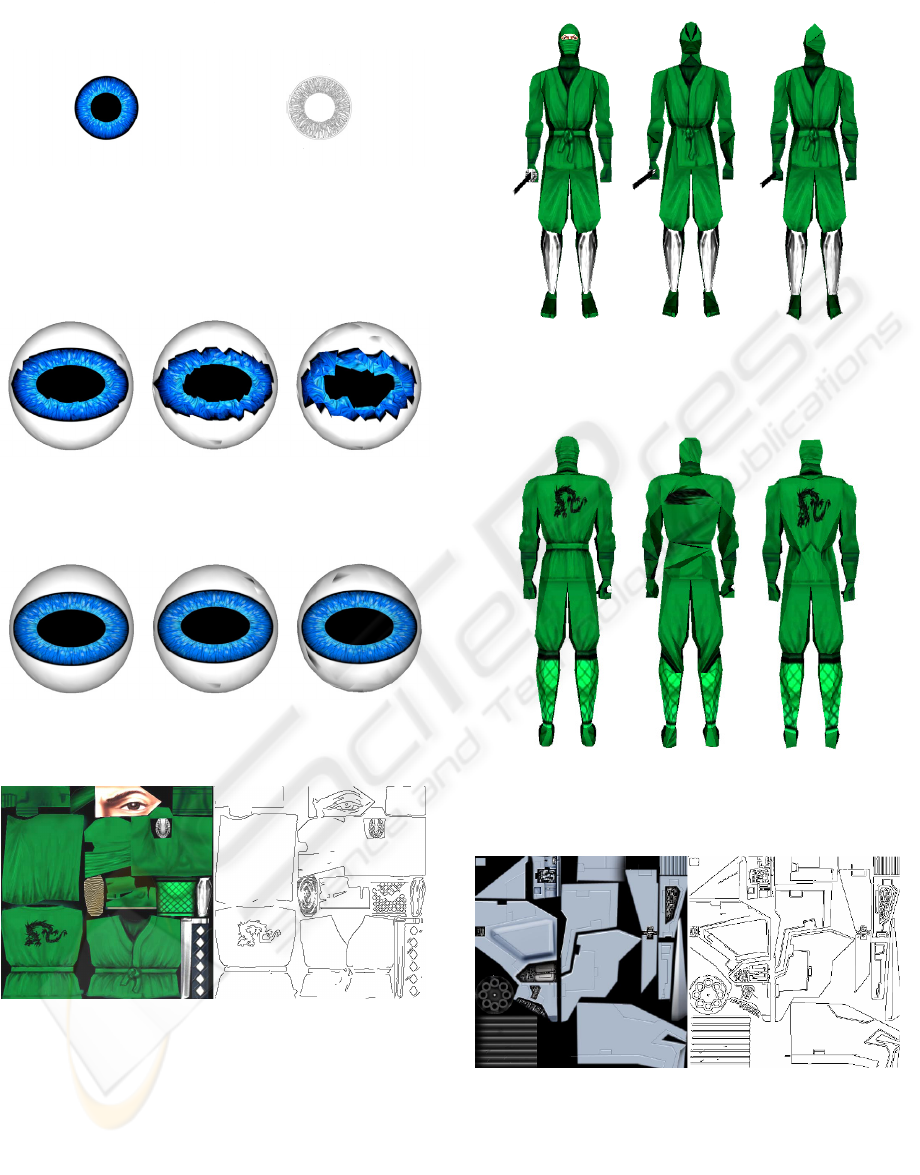
Figure 8: Eye model simplified at 75% (left), 50% (centre)

and 25% (right) applying our texture-based error metric.

Figure 6: Borders of the Eye model detected by the edge

detector method with sigma = 0.75, low threshold= 0.5

and high threshold = 0.6.

Figure 7: Eye model simplified at 75% (left), 50% (centre)

and 25% (right) without applying our texture-based erro

metric.

Figure 9: Borders of the Ninja model detected by the edge

detector method with sigma = 0.75, low threshold= 0.5

and high threshold = 0.6.

Figure 10: Front of the Ninja model. Original model (left)

and the model simplified at 50% without applying ou

texture-based error metric (centre) and applying it (right).

Figure 11: Back of the Ninja model. Original model (left)

and the model simplified at 50% without applying ou

texture-based error metric (centre) and applying it (right).

Figure 12: Borders of the Robot model detected by the

edge detector method with sigma = 0.75, low threshold =

0.5 and high threshold = 0.6.

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications

5 CONCLUSIONS

A texture-based error metric extension for

simplification methods that uses edge collapse

operations has been presented. With this extension,

the simplification also considers the texture

information of textured models. It extends the error

metric of any simplification algorithm based on edge

collapses. Thus, the original error and the new error

based on texture information are both used in the

weighting of the edges.

When extending the previous error with this

metric, the simplification order of the regions that

previously had a similar collapse cost may change.

After applying the metric, edge collapses would be

produced earlier in the regions with fewer changes

in the texture. Thus, the regions with great changes

in the texture are simplified later than the others that

have fewer changes in the texture and a similar

previous error. This method therefore avoids the

early simplification of triangles which contain

abrupt changes in the texture, which prevents great

texture distortions from appearing in simplified

models.

In consequence, this method is very useful for

multiresolution models, because it does not have to

store new texture coordinates at each step.

Figure 16: Front of Toonturtle model. Original model

(left) and the model simplified at 25% without applying

our texture-

ased error metric (centre) and applying it

(right).

Figure 17: Back of Toonturtle model. Original model (left)

and the model simplified at 25% without applying ou

texture-based error metric (centre) and applying it (right).

Figure 13: Front of Robot model. Original model (left) and

the model simplified at 50% without applying our texture-

based error metric (centre) and applying it (right).

Figure 14: Back of Robot model. Original model (left) an

the model simplified at 50% without applying our texture-

based error metric (centre) and applying it (right).

Figure 15: Borders of the Toonturtle model detected by

the edge detector method with sigma = 0.75, low

threshold= 0.5 and high threshold = 0.6.

A TEXTURE-BASED METRIC EXTENSION FOR SIMPLIFICATION METHODS

The computational cost introduced by this metric

is negligible in comparison to the simplification

cost.

Thus, this paper presents a way of extending the

error metric of the simplification methods in order to

take the textures into account.

ACKNOWLEDGEMENTS

This work has been supported by the Spanish

Ministry of Education and Science (MATER project

- TIN2004-07451-C03-03, TIN2005-08863-C03-

03), the European Union (GAMETOOLS project

IST-2-004363), the Jaume I University

(PREDOC/2005/12) and FEDER funds.

REFERENCES

Canny., J. (1983). A variational approach to edge

detection. In AAAI-83.

Canny, J. F. (1986). A computational approach to edge

detection. IEEE Trans. Pattern Analysis and Machine

Intelligence, 679-698.

Chen, C.-C., Chuang, J.-H. (2006). Texture Adaptation for

Progressive Meshes. Eurographics06-Geometry

Compression and Decompression.

Cohen, J., Olano, M., Manocha, D. (1998). Appearance-

Preserving Simplification. Proceedings of ACM.

SIGGRAPH 98. 115-122.

Garland, M., Heckbert, P. S. (1997) Surface Simplification

Using Quadric Error Metrics. Computer Graphics

(SIGGRAPH 97 Proceedings), 209-218.

Garland, M., Heckbert, P. S. (1998). Simplifying Surfaces

with Color and Texture Using Quadric Error Metrics.

Ninth IEEE Visualization 1998 (VIS'98), 264.

Garland, M., Zhou, Y. (2005, April) Quadric-based

Simplification in any Dimension. ACM Transactions

on Graphics, 24(2). Draft preprint available as Tech

Report UIUCDCS-R-2004-2450.

Hoppe, H. (1996). Progressive Meshes. Computer

Graphics (Proc. Siggraph 96), vol. 30, ACM Press,

New York, pp. 99-108.

Hoppe, H. (1999) New Quadric Metric for Simplifying

Meshes with Appearance Attributes, Proc. IEEE

Visualization 99, IEEE CS Press, Los Alamitos, Calif.,

pp. 59-66.

Lee C.H., Varshney A., Jacobs D.W. (2005). Mesh

saliency. ACM Trans. Graph. 24, 3, pp. 659-666.

Lindstrom P., Turk G. (2000, July). Image-driven

simplification. ACM TOG 19, 3, 204-241.

Luebke D.P., Hallen B. (2001) Perceptually-driven

simplification for interactive rendering. Proc. of the

12th Eurographics Workshop on Rendering

Techniques (London, UK), 223-234.

Sander, P., Snyder, J. Gortler, S., Hoppe, H.

(2001).Texture mapping progressive meshes. Proc.

SIGGRAPH, 409-416.

Williams N., Luebke D., Cohen J.D., Kelley M., Schubert

B. (2003). Perceptually guided simplification of lit,

textured meshes. Proc. of the 2003 symposium on

Interactive 3D graphics (New York, NY, USA), ACM

Press, 113-121.

Xu, A., Sun, S., Xu, K. (2005). Texture Information

Driven Triangle Mesh Simplification. Computer

Graphics and Imaging.

Zhang E., Turk G. (2002, November). Visibility-guided

simplification. Proc. of IEEE Visualization 2002,

vol.31, pp. 267-274.

GRAPP 2007 - International Conference on Computer Graphics Theory and Applications