CLOCK CONTROL SEQUENCE RECONSTRUCTION IN THE
GENERALIZED SHRINKING GENERATOR
Slobodan Petrovi
´
c
NISlab, Department of Computer Science and Media Technology, Gjøvik University College, P.O. box 191, 2802 Gjøvik, Norway
Keywords:
Cryptanalysis, Shrinking generator, Edit distance, Correlation attack.
Abstract:
An algorithm is presented that reconstructs the clock control sequence in the generalized shrinking generator
in the presence of noise. The shrinking generator is first reduced to a step 1/step E generator, where E depends
on the maximum length of runs of zeros in the output sequence of its clocking part. Then a directed depth-
first like search for optimal and suboptimal paths in the edit distance matrix corresponding to the generator
is performed. The permitted path weight deviation from the optimum is determined by the noise level in the
statistical model of the generator. Since the algorithm is deterministic, the correct clock control sequence
is guaranteed to be found, unlike many known algorithms of this kind. Experimental results show that the
algorithm converges to the correct solution relatively fast even if the noise level is high.
1 INTRODUCTION
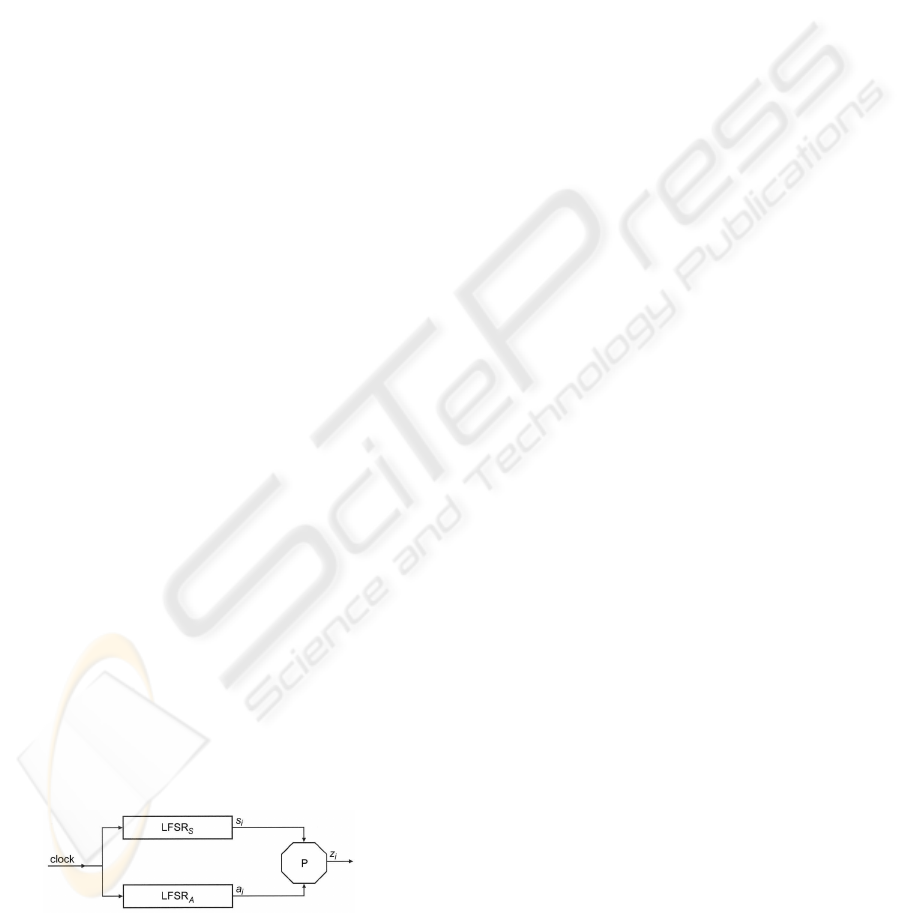
The shrinking generator (Coppersmith et al., 1994) is
a well known pseudorandom sequence generator with
irregular clocking that consists of two linear feedback
shift registers, LFSR
A
and LFSR
S
(Fig. 1). If the out-
put sequence from LFSR
A
is a = a
1
, a
2
, . . ., and the
output sequence from LFSR
S
is s = s
1
, s
2
, . . ., then the
output sequence z = z
1
, z
2
, . . . of the shrinking gen-
erator is the sequence obtained from a by removing
all a
i
’s for which s
i
= 0. The basic scheme of the
shrinking generator can obviously be generalized in
that LFSR
A
and LFSR
S
can be replaced by general
type subgenerators.
In (Goli
´
c and Mihaljevi
´
c, 1991), it was shown
for a general type pseudorandom generator with ir-
regular clocking that, by making use of a statistical
model employing constrained edit distance, it is pos-
sible to determine a set of candidate initial states of
the clocked LFSR (in this case LFSR
A
) which could
generate the intercepted output sequence.
Figure 1: The shrinking generator.
Once the set of candidate initial states is known,
the attack continues by determining the clock control
sequence that, together with one of the candidate ini-
tial states of the clocked LFSR, could generate the in-
tercepted sequence.
In this paper, we develop a deterministic method
of reconstruction of clock control sequence in the
generalized shrinking generator for the ciphertext
only attack scenario. Such a generator is first re-
duced to a step 1/step E generator, where E depends
on the maximum length of runs of zeros in the output
sequence of its clocking part. Then a ”depth-first”-
like search through the constrained edit distance ma-
trix associated with every candidate initial state of the
LFSR
A
is used. The paths in this matrix that corre-
spond to the candidate clock control sequences are re-
constructed. Influence of noise is taken into account
by relating the noise level with the permitted weight
deviation from the optimum path weight used in the
search process. By starting with the reconstruction
of paths whose weight deviation from the optimum is
0 (the optimal paths - without noise) and then by in-
creasing this weight deviation according to the noise
level (the suboptimal paths), we make our search a
directed one.
2 REDUCTION TO THE STEP
1/STEP E GENERATOR
Consider the shrinking generator from the Fig. 1, with
LFSR
S
eventually replaced with a general type sub-
generator. In the rest of the article we call this block
the clocking part of the generator. Each run of zeros
259
Petrovi
´
c S. (2007).
CLOCK CONTROL SEQUENCE RECONSTRUCTION IN THE GENERALIZED SHRINKING GENERATOR.
In Proceedings of the Second International Conference on Security and Cryptography, pages 259-262
DOI: 10.5220/0002118402590262
Copyright
c
SciTePress
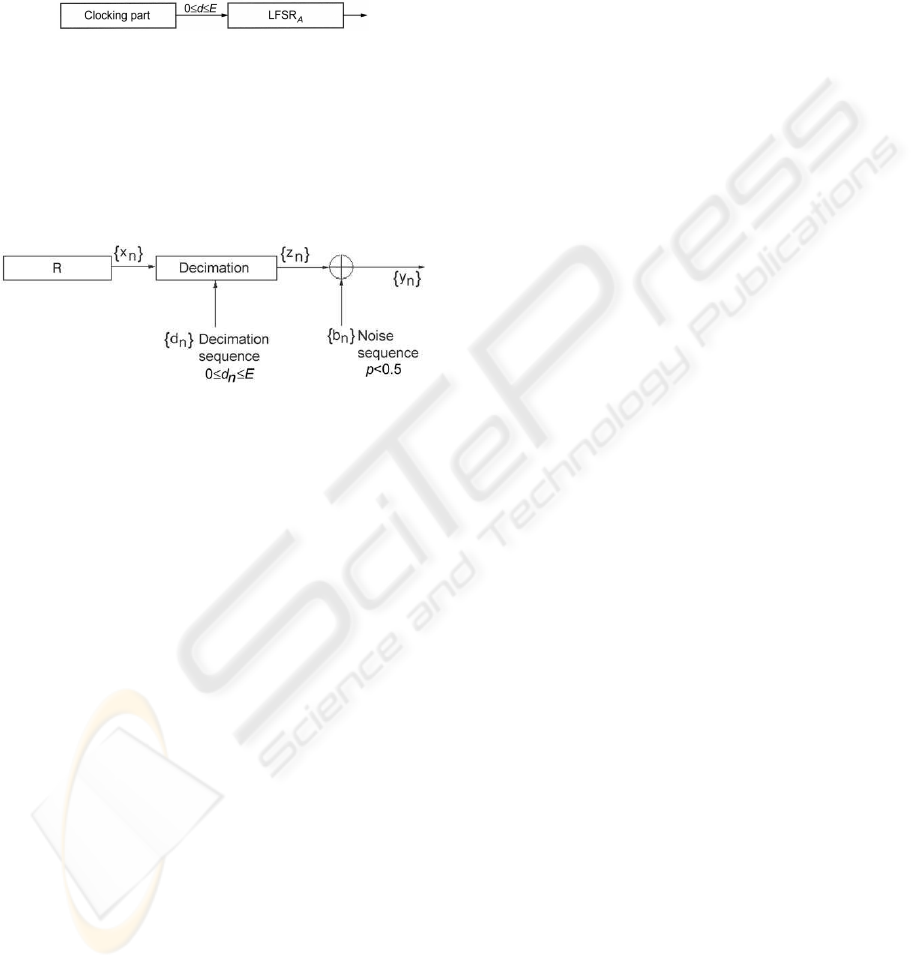
in the output sequence s of the clocking part of the
generator produces a run of deletions in the output se-
quence a of the LFSR
A
. The maximum length of runs
of deletions is equal to the maximum length E of runs
of zeros in the sequence s. Thus, instead of the shrink-
ing generator from Fig. 1, it is possible to analyze the
equivalent step 1/step E generator presented in Fig. 2.
Figure 2: The step 1/step E generator equivalent to the gen-
eralized shrinking generator.
In the reconstruction of the clock control sequence
in the generalized shrinking generator, it is possible to
use the statistical model of the step 1/step E generator
(Fig. 3). The register R in this model corresponds to
the LFSR
A
from the Figs. 1 and 2, without decima-
tion.
Figure 3: The statistical model of the step 1/step E genera-
tor.
Let {x
n
} be the binary sequence produced by the
shift register R. Let {d
n
} be a sequence of integers,
named decimation sequence, 0 ≤ d
n
≤ E, where E
is given in advance. In the decimation process, the
sequence {z
n
} is obtained in the following way:
z
n
= x
f(n)
, f(n) = n+
n
∑
i=0
d
i
, n = 0, 1, 2, . . . (1)
The correlation attack described in (Goli
´
c and Mi-
haljevi
´
c, 1991) is based on the edit distance measure
with the constraint on the maximum length of runs
of deletions. This edit distance can be determined in
an iterative way, by filling the matrix of partial con-
strained edit distances. For the rest of the paper, we
use the term edit distance matrix, for simplicity. In
the edit transformation, if e represents the number of
deletions and s represents the number of substitutions,
then the edit distance between the prefix X
e+s
of the
sequence X and the prefix Y
s
of the sequence Y is
given by the following expression:
W[e, s] = min{W[e− e
1
, s− 1] + e
1
d
e
+ d(x
e+s
, y
s
) |
max{0, e−min{N−M, (s−1)E}} ≤ e
1
≤ min{e, E}}
s = 1, . . . , M e = 1, . . . , min{N − M, sE}, (2)
where d
e
represents the elementary edit distance as-
sociated with a deletion (we assume that this value is
constant), d(x, y) represents the elementary edit dis-
tance associated with the substitution of the symbol
x by the symbol y and E is the maximum number of
consecutive deletions. From now on, we assume that
d(x, y) = 0 iff x = y. The constrained edit distance
between X and Y is obtained at W[N − M, M].
In the first phase of the attack (see (Goli
´
c and Mi-
haljevi
´
c, 1991)), the length N of the output sequence
of the LFSR R without decimation is estimated. In or-
der to reduce additional noise generated by estimation
of N, we use the mathematical expectation of N cal-
culated on the basis of the mathematical expectation
of E. It is also necessary to determine the threshold T
needed for the classification of the initial states of R.
This is done by using the probability of ”false alarm”
P
f
as well as the probability of ”missing the event”
P
m
, which are selected in advance. For every pos-
sible initial state of R, the constrained edit distance
between its corresponding output sequence of length
N and the intercepted sequence of length M is com-
puted. All the initial states that produce the output
sequences from R, whose edit distance from the inter-
cepted output sequence is less than the threshold T,
are included in the set of candidate initial states.
3 CLOCK CONTROL SEQUENCE
RECONSTRUCTION
We call the optimal paths the paths through the edit
distance matrix that begin at W[N − M, M]. Let pl ≤
M be the length of the clock control sequence needed
to reconstruct the initial state of the subgenerator
mentioned above. The optimal paths pass through
the cells W[e
p
1
, pl], . . . ,W[e
p
n
, pl] in the column pl
of the matrix W, where n depends on the particular
sequences.
To determine the points in the column pl, through
which the optimal paths pass, every cell W[e, s] has,
besides the value c of the edit distance, four associated
vectors:
1. The vector of ’primary’ pointers
vp to the cells W[vp[1], s − 1], . . . ,
W[vp[k], s − 1] from which it is possible to
arrive to the cellW[e, s] with the minimum weight
increment, k ≤ E + 2.
2. The vector of ’updated’ point-
ers vu to the cells W[vu[1], pl], . . . ,
W[vu[l], pl], through which it is possible to
arrive to the cellW[e, s] with the minimum weight
increment, l ≤ min{N − M + 1, E(1+ pl)}.
SECRYPT 2007 - International Conference on Security and Cryptography
260

3. The vector of pointers ve to the cells W[ve[1], s −
1], . . . , W[ve[ j], s− 1] from which it is possible to
arrive to the cell W[e, s] regardless of the weight
increment, j ≤ E +2.
4. The vector of values v j of the edit distances cor-
responding to the elements of the vector ve. The
cardinality of this vector is also j.
The actual values of k, l, and j depend on the par-
ticular sequences. The matrix W is filled by means of
the algorithm, which implements the equation (2) to-
gether with the updating of the four vectors mentioned
above. The complete algorithm is given below:
Algorithm 1
Input:
• The sequences X and Y of lengths N and M, re-
spectively.
• The necessary length pl of the optimal/suboptimal
path to be reconstructed.
• The maximum length E of runs of deletions (note
that we use the mathematical expectation of E).
• The elementary distance d
e
associated with the
deletion of a symbol.
• The elementary edit distance d[x, y] associated
with the substitution of the symbol x with the sym-
bol y, ∀(x, y).
Output:
• The array W of edit distances with the vectors vp,
vu, vj, and ve associated with every cell.
comment Initialization
s
max
←− min{N, M} ;
e
max
←− max{min{N − s, s∗ E}}, s = 1, . . . , s
max
;
W[e, s].c ←− ∞ , e = 0, . . . , e
max
, s = 0, . . . , s
max
; the
vectors vp, vu, v j, and ve associated with every cell
W[e, s] are empty.
W[0, 0].c ←− 0 ;
comment Main loop
for s ←− 1 until s
max
do
begin
for e ←− 1 until min{N − s, s∗ E} do
begin
Let q be the minimum value of the expression
W[e− e
1
, s− 1].c+ e
1
∗ d
e
+ d[X[e+ s],Y[s]],
e
1
= max{0, e− min{N − s, (s− 1) ∗E}}, . . . ,
min{e, E}, (3)
Let n
q
be the number of values of e
1
for which the
expression (3) takes the value q. Then
W[e, s].c ←− q ; W[e, s].k ←− n
q
;
W[e, s].vp is filled with n
q
values of the expression
(e− e
1
) corresponding to the values e
1
for which
the expression (3) takes the value q. W[e, s].vj
is filled with all the values of the expression (3).
W[e, s].ve is filled with the values (e − e
1
) corre-
sponding to the values of W[e, s].v j.
end ;
comment Determining updated pointers vu.
if s = pl + 1 then
W[e, s].vu ←− W[e, s].vp,
e = 0, . . . , min{N − s, s∗ E} ;
else if s > pl + 1 then
For every element of W[e, s].vp, e =
0, . . . , min{N − s, s ∗ F}, the elements of
W[W[e, s].vp[i], s − 1].vu, i = 1, . . . ,W[e, s].k
are placed into W[e, s].vu, deleting the repeated
ones.
end.
From now on, by paths we mean fragments of
paths that start in the column pl of the matrix W.
There are three sets of paths to be reconstructed. The
first one consists of optimal paths that start at the
points e
p
i
= W[N − M, M].vu[i], i = 1, . . . ,W[e, s].l.
The second one consists of suboptimal paths, whose
weight-difference from the optimal ones is ≤
D ,
a threshold given in advance that depends on the
noise level, that start at e
p
i
= W[N − M, M].vu[i], i =
1, . . . ,W[e, s].l. The third set consists of suboptimal
paths, whose weight-difference from the optimal ones
is ≤
D , that start at other points in the column pl.
The coordinates of the vector W[N − M, M].vu at
the end of the execution of the Algorithm 1 repre-
sent the initial points of the search for the elements
of the first and second set mentioned above. As
for the third set, if | W[e
p
i
, pl].c − W[e, pl].c |≤
D ,
e = 0, . . . , min{N − M, sE}, e 6= e
p
i
, for at least one i,
then the point W[e, pl] is an initial point of the search
for the paths of the third set.
In order to determine the optimal and suboptimal
paths that start at every initial point
E of any set, a
special depth-first like search algorithm was devised.
In this algorithm, every branching point is processed
by enumerating systematically all the paths that start
in it. In this search, a special kind of stack is used.
A reconstructed path is rejected if at some point its
weight becomes greater than the optimal weight plus
D . The complete algorithm is given below:
Algorithm 2:
Input:
• The array W of edit distances, obtained by means
of the Algorithm 1.
• The values of pl,
E and D .
Output:
CLOCK CONTROL SEQUENCE RECONSTRUCTION IN THE GENERALIZED SHRINKING GENERATOR
261
• All the paths that start at the point W[E , pl] that
belong to the corresponding set(s) (see text).
repeat
Starting from the cell W[E , pl], reconstruct in the
depth-first manner all the paths, whose weight-
differences from the optimal paths are ≤
D . On
each examined path, the cells of the array W to be
processed after the current cell W[e, s] are deter-
mined by the pointer vector W[e, s].ve (see Algo-
rithm 1).
until all the paths have been examined.
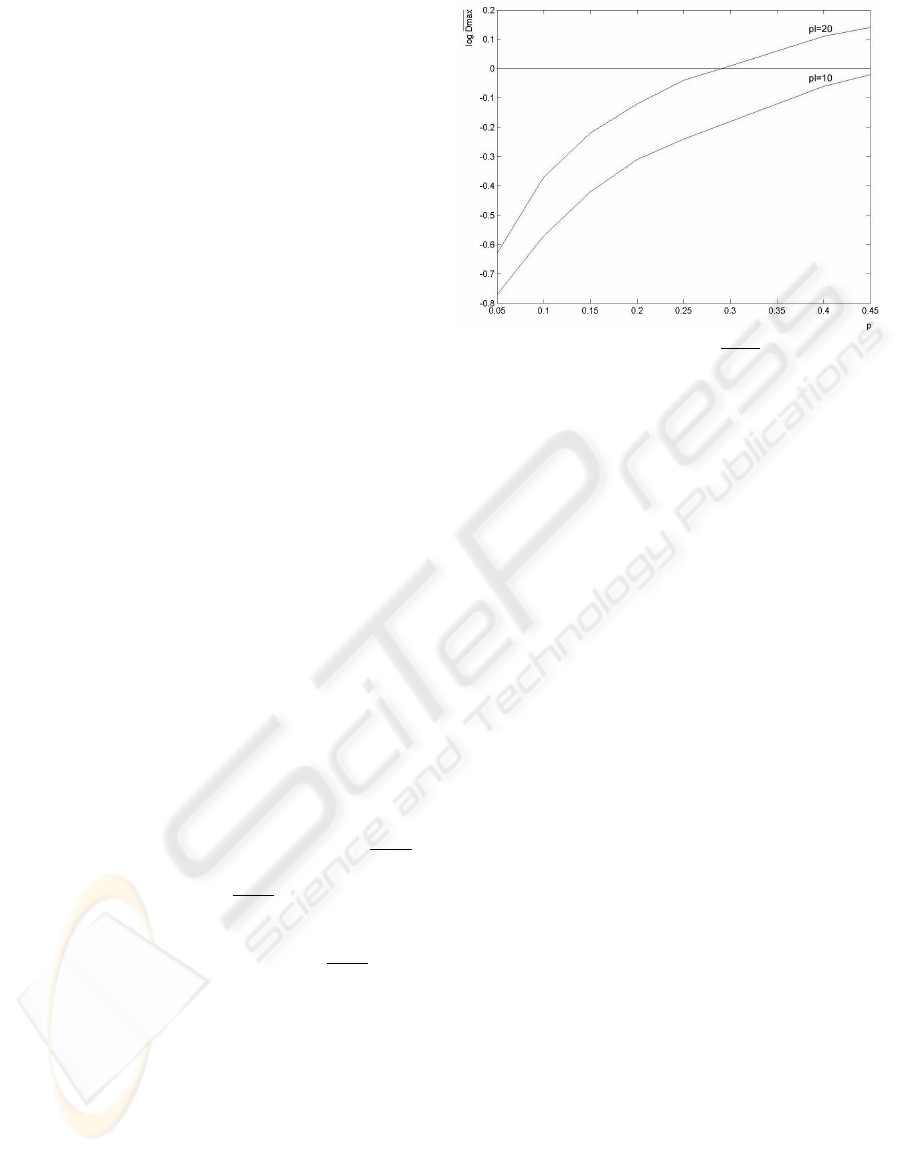
4 EXPERIMENTAL RESULTS
The number of paths necessary to find the clock con-
trol sequence increases with
D . Because of that, given
certain level of noise in the statistical model of the
generator, the behaviour of the maximum value of D ,
denoted by
D
max
, was analysed experimentally.
The experiment was carried out in the following
way: 1000 initial states of the shrinking generator
were chosen at random. For each of them, the out-
put sequence corrupted by the random noise sequence
was produced. The noise level p (i.e. the probability
of 1 in the noise sequence) was the control variable of
the experiment. The set of candidates for the initial
state of LFSR
A
was determined. Once the candidates
were obtained, for a fixed value of
D , the optimal
and suboptimal paths were determined from the edit
distance matrix corresponding to each of them. This
process was repeated starting from
D = 0 and incre-
menting the value of
D until the correct clock control
sequence generated by LFSR
S
was found. The maxi-
mum value D
max
obtained in this process was stored.
At the end of the experiment, the mean value
D
max
over the values of
D
max
obtained in every case was
computed. The dependence of
D
max
on p for two dif-
ferent values of pl is depicted in the Fig. 4.
It can be observed from the Fig. 4 that even for
high levels of noise, the obtained values of
D
max
were
relatively small for the chosen values of pl, which
means relatively fast convergence of the clock control
sequence reconstruction algorithm.
5 CONCLUSION
In this paper, a deterministic method of clock control
sequence reconstruction in the shrinking generator in
the presence of noise is described. The influence of
noise is taken into account by relating the noise level
with the permitted deviation from the noiseless-case
Figure 4: Dependence of D
max
on p.
path weight in the clock control sequence reconstruc-
tion process. The shrinking generator is first reduced
to a general step 1 / step E generator, where E is the
maximum length of runs of zeros in the clock control
sequence. Then, the statistical model of the step 1 /
step E generator that employs the constrained edit dis-
tance is used to obtain the edit distance matrix associ-
ated with every candidate initial state of the LFSR
A
.
The clock control reconstruction is performed by a di-
rected depth-first like search through the edit distance
matrix. The search starts with the reconstruction of
the paths with zero deviation from the noiseless case
path weight and then this deviation is iteratively in-
cremented. The maximum value of weight deviation
necessary for the reconstruction of the actual clock
control sequence depends on the noise level. Exper-
imental results show that the average deviation from
the noiseless case increases moderately with the noise
level, which means that the clock control sequence
reconstruction procedure converges relatively rapidly
even for higher levels of noise.
REFERENCES
Coppersmith, D., Krawczyk, H., and Mansour, Y. (1994).
The shrinking generator. In Procceings of Crypto 93,
Lecture Notes in Computer Science 773, pages 22–39.
Springer-Verlag.
Goli
´
c, J. and Mihaljevi
´
c, M. (1991). A generalized cor-
relation attack on a class of stream ciphers based
on the levenshtein distance. Journal of Cryptology,
3(3):201–212.
SECRYPT 2007 - International Conference on Security and Cryptography
262
