PRACTICAL SECURE BIOMETRICS USING SET INTERSECTION

AS A SIMILARITY MEASURE

Daniel Socek, Dubravko

Culibrk

CoreTex Systems LLC, 2851 S Ocean Blvd. 5L, Boca Raton, FL 33432, USA

Vladimir Bo

zovi

Dept. of Mathematical Sciences, Florida Atlantic University, Boca Raton, FL 33431, USA

Keywords:

Biometrics security, fuzzy one-way functions.

Abstract:

A novel scheme for securing biometric templates of variable size and order is proposed. The proposed

scheme is based on new similarity measure approach, namely the set intersection, which strongly resem-

bles the methodology used in most current state-of-the-art biometrics matching systems. The applicability of

the new scheme is compared with that of the existing principal schemes, and it is shown that the new scheme

has clear advantages over the existing approaches.

1 INTRODUCTION

Identity theft represents the fastest growing type of

fraud in the United States (Elbirt, 2005). While iden-

tity theft often occurs because of the victim’s negli-

gence, it can also occur as a result of direct tampering

with the authentication system by a criminal.

Authentication systems based on user’s biometric

data have several advantages over other authentication

methods. The main advantages of biometric-based

authentication is the simplicity of use and a limited

risk of losing, stealing, or forging users’ biological

identiﬁers. On the other hand, the major disadvan-

tage of biometrics-based authentication is the non-

renewability of biological identiﬁers. This is a par-

ticularly signiﬁcant issue regarding the identity theft

problem.

Biometric-based authentication with the same bio-

metrics is likely to be used in multiple application

systems. For example, a ﬁngerprint-based authentica-

tion could be used to gain access to multiple systems

or facilities. If a biometric template is stolen from a

authentication system, criminals can abuse it in the

present or future time in multiple venues. In addition,

to respect valid privacy concerns by the users, such as

corrupt employees at the trusted institutions that have

access to a database of biometric templates, the tem-

plates should not be stored as plaintext (in its clear

form). One solution to the problem is to make use

of tamper resistant systems; however, the use of such

systems could be infeasible in a given system setup.

Biometric templates often contain condensed dis-

criminatory information about the biometric unique-

ness of the user. For instance, in case of ﬁnger-

prints, the system often stores the discriminatory set

of minutiae points. With this information, an ad-

versary can bypass the access control system or ex-

tract certain system-speciﬁc keys provided that tam-

pering with the system at that level is feasible. In

addition, this information could potentially also be

used to perform attacks even from the topmost sensor

level by creating fake biometric identiﬁers with the

same discriminatory biometric features. For instance,

given ﬁngerprint minutiae, an attacker can construct

a fake ﬁngerprint that has the same discriminatory

information. Methods for creating fake ﬁngerprints

such as SFINGE by Cappelli, Miao and Maltoni (Cap-

pelli et al., 2002) or synthetic generation technique

by Araque et al. (Araque et al., 2002) can be used

for exactly that purpose. Uludag and Jain (Uludag

et al., 2004) described many attacks on ﬁngerprint-

based identiﬁcation systems using a fake ﬁngerprint

such as rubber or silicon ﬁnger, and alike. Similar ar-

guments are also applicable to the other types of bio-

metrics.

Clearly, standard cryptographic one-way primi-

tives are unsuitable for this purpose since the bio-

metric identiﬁers are fuzzy (not exactly reproducible)

Socek D., Ä ˛Eulibrk D. and Božovi

c V. (2007).

PRACTICAL SECURE BIOMETRICS USING SET INTERSECTION AS A SIMILARITY MEASURE.

In Proceedings of the Second International Conference on Security and Cryptography, pages 25-32

DOI: 10.5220/0002123900250032

 SciTePress

as a result of imperfections in both acquisition and

feature extraction methodologies. As a result, sev-

eral schemes for storing biometric templates securely

were proposed recently. In Section 2 of this paper, we

present a brief summary of principal work in this area

and point out a number of limitations of several state-

of-the-art methods for securing biometric templates.

In Section 3, we propose a novel approach to securing

biometric templates that has several clear advantages

over other principal approaches. Finally, conclusions

and a number of topics for further research are given

in Section 4.

2 RELATED WORK

Before describing and analyzing properties of the

principal schemes that have been proposed up to date,

and also to set the stage for later discussion, several

preliminary deﬁnitions and concepts are presented

next.

2.1 Basic Deﬁnitions

The design of a scheme for securing biometric tem-

plates is constrained with a type of biometric feature

vector that is extracted from the sensory information.

Properties of feature vectors representing biometric

templates heavily depend on the type of biometric

data involved, capability of a sensor, and the corre-

sponding feature extraction algorithm. These proper-

ties include the types of errors introduced during data

acquisition process, as well as the expected range of

values and similarity thresholds.

Typically, two types of biometrics templates (fea-

ture vectors) often appear in practice: (1) templates

with points that have constant size and order, here

denoted by type I templates, and (2) templates with

points having variable size and order, denoted by type

II templates. For example, type I biometric tem-

plates often appear in face recognition systems where

feature vectors are singular value decomposition of

a face image, or in iris recognition systems such as

IrisCode (Hao et al., 2006). Fingerprint and palm

print minutiae-based recognition systems, which con-

stitute what are the most common biometric systems

(Maltoni et al., 2003) work with type II templates.

Schemes for securing biometric templates are in gen-

eral designed for a particular template type.

In terms of application requirements, there are

several types of schemes for securing biometric tem-

plates. In work by Dodis et al. (Dodis et al., 2004;

Dodis et al., 2006), two types of schemes are deﬁned:

1. Secure sketch – This scheme essentially allows for

the precise reconstruction of a noisy input. Given

an input x, the scheme produces a public value

f(x), called secure sketch, from which no infor-

mation about x can be deduced (i.e. f is a one-

way function). The scheme can recover the orig-

inal value of x solely from f (x) and y if and only

if y is similar to x according to some similarity

measure, denoted with y ∼ x.

2. Fuzzy extractor – For a given input x this scheme

produces a public value f(x) and a secret value

k. Function f is a one-way map so that no infor-

mation about x can be deduced from f(x). The

scheme is able to recover k solely from y and f(x)

if and only if y ∼ x. In practice, k is often used as

a secret key for further cryptographic processing.

In (Dodis et al., 2006), it was also shown that it

is always possible to construct fuzzy extractors from

secure sketches. Intuitively this means that secure

sketches comply with a stronger condition (or require-

ment) than fuzzy extractors do. However, in a number

of biometrics-based security applications, even fuzzy

extractors comply to a stronger requirement than what

sufﬁces in practice.

When concerned with pure veriﬁcation or identi-

ﬁcation applications, ability to determine whether a

new template matches the stored one is a sufﬁcient re-

quirement. In general, a match is declared when two

templates are similar, or, in other words, with simi-

larity measure greater than some threshold t (also re-

ferred to as the similarity bound). Note that the simi-

larity function is not necessarily a metric. We deﬁne a

threshold-based similarity measuring scheme S to be

a scheme that for given one-way transformed value

f(x) and a template y determines whether the original

template x and y are similar or not:

S( f(x), y) =



similar, if s(x,y) > t;

not similar, if s(x,y) ≤ t,

where s(x,y) denotes a similarity measure of x and

y. Strictly speaking, this kind of scheme is slightly

more limited than a scheme that can compute the ac-

tual value of s(x,y) from f(x) and y; however, almost

all biometrics security systems are based on a thresh-

old similarity measure approach.

It is not too difﬁcult to observe that both secure

sketches and fuzzy extractors are also threshold-based

similarity measuring schemes. It may be of inter-

est to have schemes which are threshold-based sim-

ilarity measuring schemes that are strictly not secure

sketches.

SECRYPT 2007 - International Conference on Security and Cryptography

2.2 Previously Proposed Schemes

To secure biometric templates of type I, Juels and

Wattenberg proposed a scheme called fuzzy commit-

ment. This conceptually simple scheme is based on

error correcting codes. Let

F be a ﬁeld, and C the set

of vectors of some t-error correcting code. Let x ∈

denote a biometric feature vector. Assuming that all

codewords lie in F

, a codeword c is selected uni-

formly at random from

C and difference ε = c− x is

computed. Next, a suitable one-way function h is se-

lected, and the pair (ε,h(c)) is published, representing

the output of fuzzy commitment scheme.

To reconstruct the original feature vector x, a sim-

ilar vector y is required, where the measure of similar-

ity is given by a certain metric. If the usual Hamming

distance between c

′

= ε + y and c is less than t, the

error correcting capability of the code

C , then it is

possible to reconstruct c and consequently x. Since

the feature vectors are required to be from F

, the

scheme can be applied only to type I feature vec-

tors, where constant size and order is assumed. Fuzzy

commitment is a secure sketch scheme. A scheme

based on fuzzy vault principle was constructed and

successfully applied for securing a particular type of

iris templates, called IrisCode, as described in (Hao

et al., 2006).

Juels and Sudan in (Juels and Sudan, 2002; Juels

and Sudan, 2006) proposed a scheme, called fuzzy

vault, that slightly extends the applicability of a

scheme from (Juels and Wattenberg, 1999) by allow-

ing for the order invariance of feature vector coor-

dinates. This scheme substantially relies on Reed-

Solomon error correcting codes, where the codewords

are polynomials over a ﬁnite ﬁeld

F . Given a feature

vector (set) x ⊂

F and a secret value k, a polynomial

p ∈

F [X] is selected so that it encodes k in some way

(e.g., has an embedding of k in its coefﬁcients). Then

an evaluation of the elements of x against p is com-

puted and, along with these points, a number of ran-

dom chaff points that do not lie on p is added to a

public collection R.

To recover k, a set y similar to x must be presented.

If y ∼ x, then y contains many points that lie on p.

Using error correction procedure, it is possible to re-

construct p exactly, and thereby k. If y is not simi-

lar to x, it does not overlap substantially with x and

thus it is not possible to reconstruct p using the er-

ror correction mechanism of Reed-Solomon code. By

observing the public value R, it is infeasible to learn

k due to the presence of many chaff points. This is

also a secure sketch scheme. While fuzzy vault does

allow for a variable order, it does require feature vec-

tor sizes to be of the ﬁxed length, thus still not fully

supporting biometrics feature vectors of type II. Sev-

eral schemes based on fuzzy vault principle were re-

ported for ﬁngerprint data in (Clancy et al., 2003) and

(Uludag et al., 2004).

One of the most serious attacks considered for

fuzzy vault-based schemes is the multiple-use attack

that the original authors did not consider in their se-

curity model. Under the multiple-use attack, the ad-

versary has public information obtained from mul-

tiple authentication systems regarding user U. The

multiple-use attack is successful if it is possible to

compromise the secret information about U (in whole

or in part) from analyzing the public information

about U from multiple systems. Schemes based on

fuzzy vault and generally any schemes that are based

on the principle of chafﬁng and winnowing (Rivest,

1998) are weak against multiple-use attack.

Suppose the same user is enrolled in k > 1 au-

thentication systems which are all based on the same

kind of biometric (e.g. ﬁngerprint) and which all

use the fuzzy vault scheme for securing biometric

feature vectors. For simpliﬁcation, let us assume

that the user’s biometric feature vector in all sys-

tems was x = {x

,...,x

}, since almost the same ar-

guments apply when these vectors are similar. Re-

call that the public information that is stored in

system i is a collection R

(i)

that contains t points

, p

(i)

)),...,(x

, p

(i)

(t)) and m

(i)

chaff points

(i)

),...,(r

(i)

). According to the fuzzy

vault speciﬁcation chaff points are selected uniformly

at random from

U − x, where U denotes the universe

of feature vector coordinates. If R

(i)

denotes the re-

striction of R

(i)

to the x-axis, then

lim

k→∞

(1)

∩ R

(2)

∩ ... ∩ R

(k)

) = x

unless chaff points always entirely cover the remain-

ing universe

U − x or some ﬁxed parts of it. More-

over, if we take a simple case when r = |R

(i)

| − t ≪

|U | for i = 1,2, then

Prob(R

(1)

∩ R

(2)

= x) =



|U |−t−r





|U |−t



+ 1

≈ 1,

where |

U | denotes the cardinality of set U . In other

words, if the number of randomly selected chaff

points is much smaller than the size of the universe

U , the intersection of chaff points of the same per-

son taken from two authentication systems will al-

most certainly be empty.

In (Juels and Sudan, 2002; Juels and Sudan, 2006)

it is shown that the number of different polynomials

that agree on t is small if the size of collection R is

small. Thus, in order to ensure security from that

PRACTICAL SECURE BIOMETRICS USING SET INTERSECTION AS A SIMILARITY MEASURE

point of view, the authors recommend taking a large

number of chaff points. Yet, the authors do not re-

quire to always cover the entire remaining universe

U − x with chaff. Indeed, this is probably infeasi-

ble when dealing with larger universes. However, to

avoid the multiple-use attack as described here, the

entire remaining universe or ﬁxed part of it must be

covered by chaff. That is, R

(i)

′

for all i where

′

is a subset of

U (likely U

′

U ) that provides a large

number of polynomials that agree on t points and also

a computationally infeasible search space.

In (Boyen, 2004), Boyen considered the issues of

multiple uses of the same fuzzy secret in a general

fuzzy extractor scheme. Boyen pointed out that in the

security model of fuzzy extractors such issue must be

addressed and related security risks accounted for.

Dodis et al. in (Dodis et al., 2004; Dodis et al.,

2006) proposed a scheme that allows for securing bio-

metric feature vectors of type II. This scheme, called

PinSketch, relies on t-error correcting (BCH) code C.

In order to simplify description, let us assume H to be

a parity check matrix of the code C over some ﬁnite

ﬁeld

F . For a given feature vector x which belongs to

, the scheme computes output syn(x) = Hx, which

is referred to as the syndrome of vector x.

In the reconstruction phase, syn(y) is computed

for a given vector y. Let δ = syn(x) − syn(y). It is

easy to see that there exists at most one vector v such

that syn(v) = δ and weight(v) ≤ t. One of the nice fea-

tures of binary BCH codes is possibility of computing

supp(v) given syn(v) and vice versa, where supp(v)

represents the listing of positions where v has nonzero

coordinate. Computing of supp(v) for a given syn(v)

is the key step in the reconstruction phase. If a dis-

tance metric d(x, y) ≤ t then supp(v) = x△y, and in

that case the original set could be reconstructed by

x = y△supp(x). PinSketch is a secure sketch scheme

that supports biometrics feature vectors of type II.

2.3 Applicability Critique of Error

Correcting-based Schemes for Type

II Templates

From the mathematical point view, the most suitable

method for measuring similarity between two sets is

by their symmetric set difference. However, this quite

reasonable mathematical choice is often a limitation

for practical use. Let us try to illustrate this problem

in the case where it is needed to measure closeness

between two sets A and B that represent biometric

(ﬁngerprint) personal data, of not necessarily differ-

ent persons. This is an inevitable step in the process

of veriﬁcation or identiﬁcation. Reconstruction of A,

using similar set B will be successful if and only if

|A△B| ≤ t, where t is a given parameter that controls

the closeness between sets. It seems that error cor-

recting codes are a suitable choice for reconstructing

A from a noisy input B. Here, t is the error correcting

bound of the chosen code.

We argue that the use of error correcting codes and

consequently the Hamming distance as a measure of

similarity between type II feature vectors is not an ad-

equate choice. For instance, in the PinSketch scheme

(Dodis et al., 2006), templates are represented as char-

acteristic vectors with respect to universe

U . There-

fore, the symmetric difference is simply related to the

Hamming distance between characteristic vectors. In

a typical application of PinSketch, such as ﬁngerprint

identiﬁcation, the scheme has a substantial applica-

bility issue. The number of minutiae, according to

many statistical analyses of ﬁngerprints lies with high

probability in the interval between 20 and 80 (Amen-

gual et al., 1997). Thus, choice of the error correcting

bound t that is used in this scheme seems to be its

main shortcoming.

Considering that size of the universe is not large,

t must be chosen in a way not to compromise secu-

rity. For instance, if a template set is of size 15, then

setting t > 12 would not be an adequate choice, since

an adversary could test all elements or 2-subsets of

the universe (which is feasible for a universe of ﬁn-

gerprint minutiae) and use error correction to obtain

the template set. On the other hand t must be set to

provide proper authentication. Due to imperfections

in the template extraction it is common to have spuri-

ous minutiae and some real minutiae that are not rec-

ognized. Thus, symmetric difference between newly

presented and stored template could became relatively

large, yet the intersection could still be large enough

for authentication of B as A with high conﬁdence. For

example, suppose |A| = 20 and |

U | ≈ 10

with pos-

sibly nonuniform distribution. Therefore, t could be

at most 17. If we accept twelve point matching rule

as valid, and if |B| = 22 and |A∩ B| = 12 then B will

not be authenticated as A although intersection is large

enough to conﬁrm the identity. Even if do not accept

twelve point matching rule, it is possible to construct

many examples where symmetric difference does not

appear as an adequate choice for similarity measure.

In most minutia-based authentication systems similar-

ity is measured using the number of points that agree

in the best possible alignment of two sets of minu-

tiae using translation, rotation and potentially scaling.

Therefore, the set intersection is a more appropriate

similarity measure in practice.

The authors of fuzzy vault (Juels and Sudan, 2002;

Juels and Sudan, 2006) indicated that the scheme is

applicable to feature vectors with ﬁxed size and vari-

SECRYPT 2007 - International Conference on Security and Cryptography

able ordering which limits the practical use of the

scheme to type I vectors. Even if it is possible to ex-

tend the fuzzy vault scheme to work with the type II

feature vectors, the scheme would face the similar ap-

plicability issues since it is based on error correction

approach. As an artifact of fuzzy vault where the en-

tire universe is covered by chaff due to multiple use

attack and the requirement about the minimal num-

ber of different polynomials that agree on t points, the

similarity measure is not achieved with symmetric set

difference but with ordinary set difference B−A. This

slightly better scenario is still inappropriate since it is

possible to have cases where both A∩B and B−A are

relatively large, in which case the fuzzy vault scheme

would give a false rejection.

In this work we design a scalable secure scheme

applicable to type II biometric templates, such as ﬁn-

gerprint minutiae which are currently the most com-

mon biometric templates (Maltoni et al., 2003).

3 OUR APPROACH

Let

F be a ﬁnite ﬁeld. Given an encoding of biomet-

ric templates into the ﬁeld

F , it is common to denote

F as the universe U . In this setting, biometric tem-

plates correspond to the subsets of

U . The key obser-

vation is that the size of the universe is typically much

larger than the size of a subset representing a biomet-

ric template, but still in a range that allows feasible ex-

haustive search. For instance, the size of the universe

representing ﬁngerprint minutiae is approximately in

the range of 10

-10

, depending on technical charac-

teristics of the sensor, yet the size of a biometric tem-

plate is between 20 and 80 with high probability. In

further analysis, we will assume |

U | ≫ |A|, where A

represents a template set.

Accuracy of the extraction of biometric data de-

pends on several factors, but mostly on the sensory

technology for data acquisition and image processing

algorithms for biometric template extraction. Due to

these imperfections, it cannot be expected that newly

submitted templates perfectly match the stored ones.

It is not uncommon to have, under certain scenarios,

just part of the ﬁngerprint that needs to be identiﬁed.

Therefore, a scheme for secure authentication needs

to have a necessary level of tolerance with respect to

possible incompleteness and inaccuracy of submitted

templates. The tolerance threshold for our scheme can

be easily customized regarding the particular applica-

tion.

3.1 Scheme Description

Let

G be a ﬁnite ﬁeld where |G | = p

, assuming that

provides a large keyspace, e.g. p

> 2

100

. Let m

and m

be integers such that m

≤ |A| ≤ m

for all

subsets A representing biometric templates. Suppose

that ℓ is an integer chosen in so that



ℓ



≤ 2

≪ 2

≤



U |

ℓ



In general, it is required for k

to be small enough to

allow for a feasible search through the set of ℓ-subsets

of any given template A. On the other hand, it is re-

quired for k

to be large enough, making it infeasible

to search through all ℓ-subsets of the universe

U . As

an illustration, under the assumption that the distribu-

tion of points of A is uniform over

U , if |U | ≈ 10

and m

= 100, even with a choice of ℓ = 3 the size



|U |

ℓ



is approximately 2

which is a larger search

space than that of DES. For the same parameters, the

size of



ℓ



is just 161700. The generation of public

one-way transformation of the given template in the

proposed scheme is as follows:

1. Let A = {a

,...,a

} the input biometric tem-

plate. Randomly choose s ∈

G and using an ℓ-out-

of-n perfect secret sharing scheme, create n shares

of s denoted by s

,...,s

2. Choose a secure cryptographic hash function h

and obtain set {h(sa

),h(sa

),...,h(sa

)}, where

means concatenation of s and a

. It is required

that the chosen hash function is both preimage re-

sistant and collision-resistant.

3. Deﬁne a discrete function f

U → G in the fol-

lowing way

(x) =



, if x = a

;

, if x /∈ A,

where the values y

are chosen uniformly at ran-

dom.

4. Store f

(x), H

= {h(sa

),h(sa

),...,h(sa

)}

and h(s) as a one-way public transformation of A.

The recovery process in our scheme is performed

in the following way:

1. For a given set B = {b

,...,b

}, for all ℓ-subsets

of B, denoted by B

,...,B

(

ℓ

)

, do the following:

(a) Evaluate f

(b) Using the reconstruction method provided by

the secret sharing scheme, obtain s

′

from

PRACTICAL SECURE BIOMETRICS USING SET INTERSECTION AS A SIMILARITY MEASURE

′

); if h(s

′

) = h(s), then assume

s = s

′

, compute H

= {h(s

′

),...,h(s

′

)},

and then output |H

∩ H

}| = |A ∩ B| ≥ ℓ and

terminate.

2. If for all ℓ-subsets of B no termination was

reached, output |A∩ B| < ℓ and terminate.

In our scheme, s corresponds to the extracted key

from the deﬁnition of fuzzy extractor. Moreover, with

minor modiﬁcations the proposed scheme can also be

turned into a secure sketch scheme where original set

A can be completely reproduced. The algorithm deter-

mines a threshold-based similarity of templates A and

B using set intersection as a similarity measure, which

reﬂects the same principle used in most minutia-based

recognition methods. The algorithm outputs |A ∩ B|

if |A ∩ B| ≥ ℓ. Once |A ∩ B| has been obtained, it is

to be decided if the authentication threshold has been

achieved.

The authentication bound is not substantially in-

volved in our scheme, which is not the case in the

previous schemes. The only requirement related to

the authentication bound is that it must be greater than

or equal to the security bound ℓ.

3.2 Security and Applicability Aspects

To address the security of our method, it is essential to

discuss issues regarding the distribution of the source

data. The attacker’s goal is to learn information about

the original template A given only the public values

(x), H

and h(S). Note that the multiple use at-

tack is not applicable to our scheme since the entire

universe

U is covered by uniformly random values

according to f

A reasonable question that arises from the anal-

ysis of the proposed scheme is how the assumption

of strictly uniform distribution could be relaxed for

some practical applications. We show how to set pa-

rameters of our scheme in the case of ﬁngerprint au-

thentication.

In our scheme, for the enrollment template A and

a probe B that originates from the same subject as A,

we assume that |A∩ B| = ⌈t|A|⌉ for t ∈ (0, 1).

Let X be a random variable that describes the

number of unsuccessful attempts before getting a

qualiﬁed subset, i.e. a set from A ∩ B. Clearly

X has a negative hypergeometric distribution. If

(b)

= a(a − 1) · · ·(a− b+ 1) than the distribution of

X is

Prob(X = r) =

(r−1)

(r)

where b =



⌈t|A|⌉

ℓ



, c =



|B|

ℓ



and w = c− b.

Then, the mathematical expectation of X is given

EX =

c+ 1

b+ 1

Next, we show some concrete parameters that

give a clear view of the computational complexity of

the searching process for an ℓ-subset in A ∩ B. In

Table 1 we ﬁx parameter t = 0.5 and for simplicity,

we ﬁx the sizes of A and B to be equal although this

is not required by our construction.

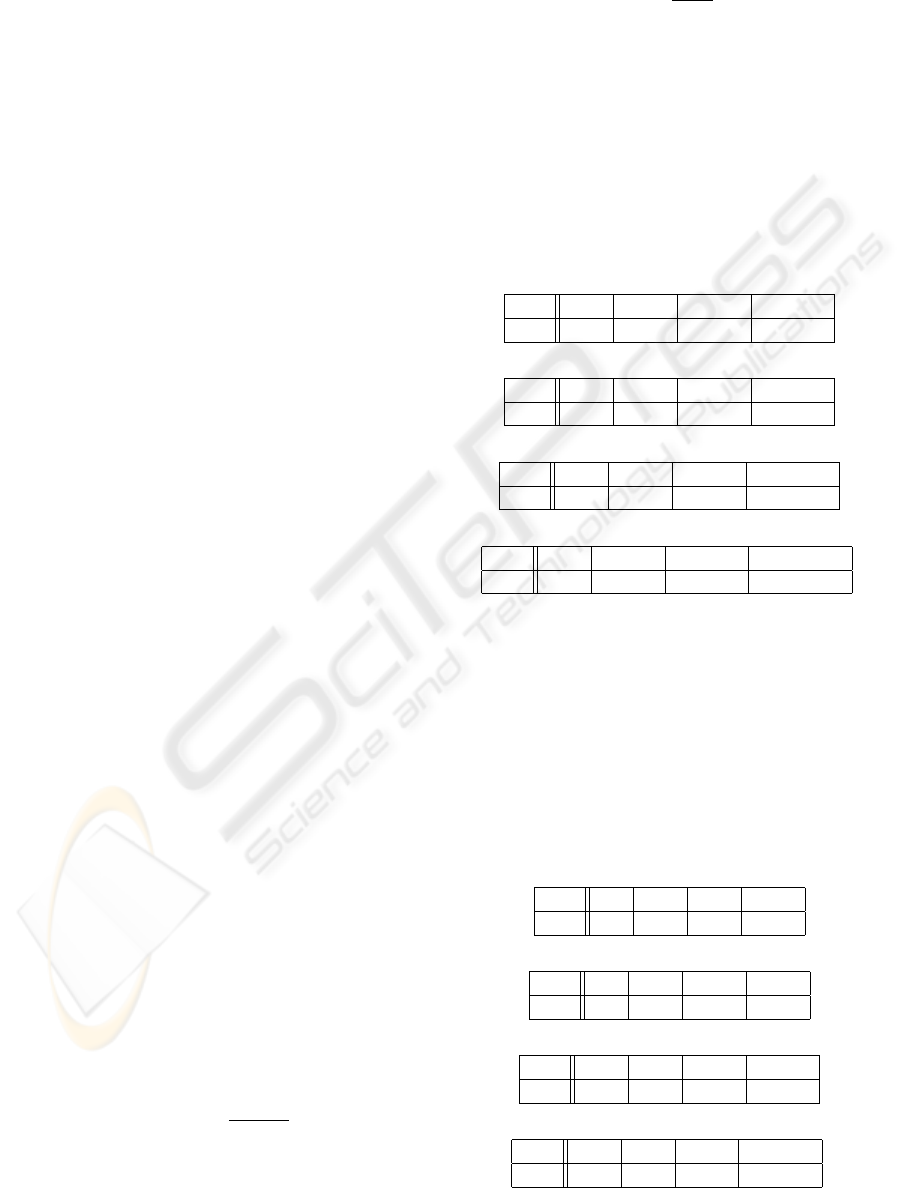
Table 1: The expected number of attempts needed to ﬁnd an

ℓ-subset of A∩ B for various sizes of A and B when t = 0.5.

|A| = |B| = 80

ℓ 8 10 12 15

EX 377 1943 10784 164968

|A| = |B| = 60

ℓ 8 10 12 15

EX 438 2510 16179 342928

|A| = |B| = 40

ℓ 8 10 12 15

EX 611 4588 44351 2594347

|A| = |B| = 30

ℓ 8 10 12 15

EX 910 10002 189679 77558761

If we set t to be slightly higher, for example

t = 0.6, then the expected values signiﬁcantly change,

as depicted in Table 2. For many authentication sys-

tems it is not unreasonable to expect that set B, which

originates from the same subject as A, have at least

60% common points with A.

Table 2: The expected number of attempts needed to ﬁnd an

ℓ-subset of A∩ B for various sizes of A and B when t = 0.6.

|A| = |B| = 80

ℓ 8 10 12 15

EX 77 252 865 6070

|A| = |B| = 60

ℓ 8 10 12 15

EX 85 297 1118 9554

|A| = |B| = 40

ℓ 8 10 12 15

EX 105 433 2067 30765

|A| = |B| = 30

ℓ 8 10 12 15

EX 134 687 4659 189863

SECRYPT 2007 - International Conference on Security and Cryptography

Although parameter t is not included in the con-

struction of the scheme, it is useful to have a pre-

sumption on the expectation for t. Taking into con-

sideration the particular application and by doing a

preliminary statistical analysis on the accuracy of the

template extraction system, an estimation for t can be

achieved. When higher level of security is required, t

generally must be higher. Consequently, it is possible

to choose larger ℓ and still have a high efﬁciency in

the task of ﬁnding ℓ-subset from A∩ B.

For instance, for certain high-security authenti-

cation, the threshold of common points between the

new and stored template could be set to at least 80%

of the stored template set. In that case, even setting

ℓ ≥ 20 results in efﬁcient performance of our scheme.

Table 3 shows the case when ℓ = 20.

Table 3: The expected number of attempts needed to ﬁnd

20-subset of A∩ B when t = 0.8 and |A| = |B| = n.

n 30 40 60 80

EX 2828 611 251 181

There have been a number of attempts to explain

the minutiae distribution. Most recent papers track-

ing this subject come from the Michigan State Uni-

versity group which mainly dealt with the questions

of individuality of ﬁngerprints and how similar two

randomly chosen ﬁngerprint templates could be. This

problem was partially inspired by a recent challenge

to the generally accepted twelve points matching rule

in some US courts.

The statistical model of distribution of minutiae

points has not been established due to very complex

nature of the problem. The distribution of minu-

tiae that has been proposed in (Dass et al., 2005) is

a so-called mixed distribution. This distribution ap-

pears to be more appropriate than the uniform distri-

bution regarding the statistical data collection taken

from three large publicly available databases of ﬁn-

gerprints (Dass et al., 2005). However, note that all

results heavily depend on the quality of acquired ﬁn-

gerprint data and the extraction method used in the

experiments.

The result which could be of particular importance

for our security model is a result about the probability

that two random ﬁngerprint templates of 36 minutiae

share more than 12 points. If P(36,36,12) denotes

this probability and assuming the mixed distribution,

it can be shown that P(36, 36, 12) ≈ 6× 10

−7

. In our

scheme, if ℓ = 12 then an attacker could try to get

stored set A of 36 minutiae by choosing a random sub-

set B of 36 elements of the universe

U , hoping that

|A∩ B| ≥ 12. However, the only way the attacker can

know if the chosen subset B contains more than 12 el-

ements of the stored template A is by running through

all 12-subsets of B. Thus, the probability of an at-

tacker’s success is ≈ 6 × 10

−7

(

)

≈ 2

−56

. That

makes this kind of attack inefﬁcient especially if we

set ℓ to be higher than 12.

We would like to stress that the previously men-

tioned results are dependent on the effectiveness of

the automated minutiae extraction methods which are

only of moderate reliability.

It must be understood that the nonuniformity of

the universe of certain biometrics inﬂuences all pro-

posed schemes regarding security issues. For the

schemes based on error correction codes, nonuni-

formity affects the error correction bound. Conse-

quently, it produces an increase of the False Rejec-

tion Rate (FRR). In our scheme, it induces an increase

of the parameter ℓ that causes a higher computational

cost.

4 CONCLUSIONS

We proposed a novel scheme for securing biometric

templates of variable size and order. Unlike previ-

ously proposed schemes, our scheme uses set inter-

section as the similarity measure between the enroll-

ment template and a probe. This principle reﬂects

matching criteria used in most minutia-based authen-

tication systems, and as such offers better applicabil-

ity than the schemes based on error correcting ap-

proach. We showed that the scheme is scalable and

has a relaxed dependency on the similarity bound. Fi-

nally we demonstrated how to set the parameters of

the proposed scheme in order to achieve both high se-

curity and broad applicability even when the minutiae

distribution is nonuniform.

ACKNOWLEDGEMENTS

The authors would like to express their gratitude to

Prof. Dr. Spyros S. Magliveras and Prof. Dr. Rainer

Steinwandt at Florida Atlantic University for their

helpful comments and suggestions.

REFERENCES

Amengual, J., Juan, A., P

erez, J., Prat, F., S

aez, S., and Vi-

lar, J. (1997). Real-time minutiae extraction in ﬁnger-

print images. In International Conference on Image

Processing and Its Applications (IPA97), volume 2,

pages 871–875.

PRACTICAL SECURE BIOMETRICS USING SET INTERSECTION AS A SIMILARITY MEASURE

Araque, J., Baena, M., Chalela, B., Navarro, D., and Viz-

caya, P. (2002). Synthesis of ﬁngerprint images. In

16th International Conference on Pattern Recogni-

tion, volume 2, pages 422–425.

Boyen, X. (2004). Reusable cryptographic fuzzy extractors.

In ACM Conference on Computer and Communica-

tions Security (CCS 2004), pages 82–91. New-York:

ACM Press.

Cappelli, R., Maio, D., and D.Maltoni (2002). Synthetic

ﬁngerprint-database generation. In 16th International

Conference on Pattern Recognition, volume 3, pages

744–747.

Clancy, T. C., Kiyavash, N., and Lin, D. J. (2003). Secure

smartcard-based ﬁngerprint authentication. In ACM

SIGMM Workshop on Biometrics Methods and Appli-

cations (WBMA ’03), pages 45–52. ACM Press.

Dass, S. C., Zhu, Y., and Jain, A. K. (2005). Statistical mod-

els for assessing the individuality of ﬁngerprints. In

IEEE Workshop on Automatic Identiﬁcation Advanced

Technologies (AUTOID ’05), pages 3–9. IEEE Com-

puter Society.

Dodis, Y., Reyzin, L., and Smith, A. (2004). Fuzzy extrac-

tors: How to generate strong keys from biometrics and

other noisy data. In EUROCRYPT 2004, Interlaken,

Switzerland, pages 523–540.

Dodis, Y., Ostrovsky, R., Reyzin, L., and Smith, A. (April

28, 2006). Fuzzy extractors: How to generate strong

keys from biometrics and other noisy data. Retrieved

April 4, 2007, from

http://www.citebase.org/

abstract?id=oai:arXiv.org:cs/0602007

Elbirt, A. J. (Summer 2005). Who are you? how to protect

against identity theft. IEEE Technology and Society

Magazine.

Hao, F., Anderson, R., and Daugman, J. (2006). Combining

crypto with biometrics effectively. IEEE Transactions

on Computers, 55(9):1081–1088.

Juels, A. and Sudan, M. (2002). A fuzzy vault scheme. In

IEEE International Symposium on Information The-

ory (ISIT 2002), Lausanne, Switzerland.

Juels, A. and Sudan, M. (2006). A fuzzy vault scheme.

Designs, Codes and Cryptography, 38(2):237–257.

Juels, A. and Wattenberg, M. (1999). A fuzzy commitment

scheme. In ACM Conference on Computer and Com-

munications Security, pages 28–36.

Maltoni, D., Maio, D., Jain, A.K., and Prabhakar, S. (2003).

Handbook of Fingerprint Recognition. Springer-

Verlag.

Rivest, R. L. (April 24, 1998). Chafﬁng and winnow-

ing: Conﬁdentiality without encryption. Retrieved

April 4, 2007, from

http://theory.lcs.mit.edu/

rivest/chaffing.txt

Uludag, U., Pankanti, S., Prabhakar, S., and Jain, A.

(2004). Biometric cryptosystems: Issues and chal-

lenges. IEEE Special Issue on Enabling Security Tech-

nologies for Digital Rights Management, 92(6):948–

960.

SECRYPT 2007 - International Conference on Security and Cryptography