USING STEGANOGRAPHY TO IMPROVE HASH FUNCTIONS’

COLLISION RESISTANCE

Emmanouel Kellinis

and Konstantinos Papapanagiotou

KPMG LLP, One Canada Square, London E14 5AG, United Kingdom

Dept. of Informatics and Telecommunications, University of Athens, Panepistimiopolis, Ilissia, Greece, GR15784

Keywords: Hash function, steganography, source code tampering.

Abstract: Lately, hash function security has received increased attention. Especially after the recent attacks that were

presented for SHA-1 and MD5, the need for a new and more robust hash function has become imperative.

Even though many solutions have been proposed as replacements, the transition to a new function could be

costly and complex. In this paper, we introduce a mode of operation that can be applied to any existing or

future hash function in order to improve its collision resistance. In particular, we use steganography, the art

of hiding a message into another message, to create a scheme, named Σ-Hash, which enforces the security of

hashing algorithms. We will demonstrate how, apart from hash function security, Σ-Hash can also be used

for securing Open Source code from tampering attacks and other applications.

1 INTRODUCTION

Cryptographic hash functions are nowadays an

essential part to the majority of cryptographic

protocols. A hash function is a process that takes an

input of arbitrary size and returns a fixed size output,

which is called hash value or message digest. Hash

functions should have the following cryptographic

properties: first, pre-image resistance dictates that

given the hash value h, it should be computationally

infeasible to find any message m so that h=hash(m).

Moreover, a hash function should also be second

pre-image resistant, which means that given a

message m1 it should be hard to find a message

m2≠m1 so that hash(m1)=hash(m2). Finally,

collision resistance impairs that it should be hard to

find two different messages m1, m2 so that

hash(m1)=hash(m2).

Most popular hash functions, such as MD5

(Rivest, 1992) and SHA-1 (NIST, 1995) construct a

hash value by applying a variant of the Merkle-

Damgård construction (Merkle, 1989) (Damgård,

1989) to a compression function. According to this

scheme, a long message is broken into equal-sized

blocks with the final block being padded to the

allowable block size. Then, a compression function

is operated on the blocks to produce the fixed size

hash value. If the compression function is collision-

resistant then so will be the hash function. Even

though the Merkle-Damgård construction ensures to

some point the security of hash functions, it also has

some vulnerabilities that can be exploited to attack

such algorithms.

Recently, various attacks (Boer, 1993) (Wang

2005) to these algorithms were presented provoking

discussions in order to propose a new, safer hashing

algorithm. Apart from the obvious problem of

security and collisions another issue has also

emerged: existing applications and cryptographic

algorithms should be able to easily migrate to a new

possible function, a task that may not be easy. The

hash transition problem, as it is referred to, has

various aspects which have been examined in

(Bellovin, 2005). Randomized hashing (Halevi,

2005) is a mode of operation that has been proposed

for strengthening hash functions. It has been

designed mainly for use in digital signatures

schemes, without requiring any alterations in the

existing algorithms and their implementation.

Here, we introduce a mode of operation for hash

functions that uses steganography to enhance

collision resistance of current and future hashing

algorithms. Steganography is used to hide a secret

message into another message that is characterized

by redundancy. In this paper we use steganographic

functions to produce hash values that are more

resistant to collisions. This mode of operation, called

Σ-Hash (Sigma Hash), can be used in conjunction

with any hashing algorithm. Due to the properties of

337

Kellinis E. and Papapanagiotou K. (2007).

USING STEGANOGRAPHY TO IMPROVE HASH FUNCTIONS’ COLLISION RESISTANCE.

In Proceedings of the Second International Conference on Security and Cryptography, pages 337-340

DOI: 10.5220/0002125203370340

 SciTePress

the steganographic algorithms it is hard for an

attacker to produce collisions for Σ-Hash.

The structure of this paper is as follows: in

section 2 we briefly describe our motivation.

Subsequently we present the basics of

steganography. In section 4 the proposed Σ-Hash

scheme is presented and analyzed. Finally, we

provide some concluding remarks.

2 MOTIVATION

Even though hash functions are carefully designed to

satisfy the required security properties, they are still

vulnerable to collision attacks. Due to their nature, it

will always be possible to find two different inputs

that will produce the same output. Using the

birthday paradox (Bellare, 2004) an attacker can find

a collision for a hash function of range r in r

1/2

operations. This is considered the simplest attacking

method, equivalent to a brute force attack. A

birthday attack is considered computationally

infeasible for modern.

Nevertheless, other more efficient techniques

have been proposed that can identify collisions in

fewer steps. The first attack in SHA-0 was presented

by Wang (Wang, 1997) in 1997. Earlier, in 1993

some form of collisions for MD5 had been found

(Boer, 1993). Recently, Wang’s team discovered

collisions in MD4, MD5, HAVAL-128, and

RIPEMD (Wang, 2005), while the authors in

(Biham, 2005) presented a technique that can be

used to find collisions in SHA-0 with a 2

complexity. Wang et al showed in (Wang, 2005) that

a collision can be found in SHA-1 with 2

computations. Even though these attacks are

theoretical, they demonstrate that the currently most

widely used hash algorithms are indeed vulnerable.

Furthermore, lately, especially with the

emergence of the open source movement, it is very

common for users to download open source

programs, compile them locally and then execute

them. This has led to a new form of attack, called

source code tampering, where a malicious user alters

the source code or even inserts arbitrary pieces into

it. A user downloading such code has no way of

knowing if the original source code has been

tampered with and of course, cannot be expected to

review every single line of code that he downloads.

Hash functions provide a means for integrity

checking which can mostly detect and correct errors

introduced by the network. A malicious user that is

able to modify the source code remotely he will as

easily be able to also modify its hash value. Such

kind of attacks may be countered with the use of

digital signatures. However, the use of digital

signatures brings along all the known issues of

public key cryptography: performance and

communication overhead, key management issues,

not to mention the growing number of identity theft

and phishing incidents.

3 STEGANOGRAPHY

Steganography concerns itself with ways of

embedding a secret message into a cover object,

without altering the properties of the cover object

evidently. The embedding procedure is typically

related with a key, called a stego-key. Without

knowledge of this key it will be difficult for a third

party to extract the message or even detect its

existence. Once the cover object has data embedded

in it, it is called a stego object. The amount of data

that can be hidden in a cover object is often referred

to as embedding capacity. The embedding capacity

is directly related with the secrecy of the message.

Usually, the distortions in the cover object caused by

the steganographic algorithm become more obvious

as a user tries to add more hidden data.

In general, any object which demonstrates

increased redundancy can be used to hide

information. Image steganography usually involves

hiding information in the Least Significant Bits

(LSB) in the spatial or frequency domain. Audio

steganography works in a similar way. Text based

steganography uses methods that are similar to those

for image and audio steganography. However, in

many cases, hidden messages in texts need to be

carefully protected since an abnormality in natural

language can be easily detected. Other techniques

include syntactic and semantic manipulation of a

given text or aesthetic manipulation, such as the

white space method. The latter involves adding

spaces or tabs at the end of words or lines.

Mark-up languages, like HTML, can be used to

store data. One can store binary values based on the

simplicity of such languages as well as the freedom

to rearrange tags without changing the displayed

page. Programming languages like C or Java have

stricter rules and thus less redundancy. One could

always use steganographic methods that are based

on aesthetic changes. For example, white space

steganography could be used as most compilers

disregard spaces and tabs. Moreover, one could

operate steganographic functions on source code

comments, or even insert carefully coded comments

in order to hide a message.

SECRYPT 2007 - International Conference on Security and Cryptography

338

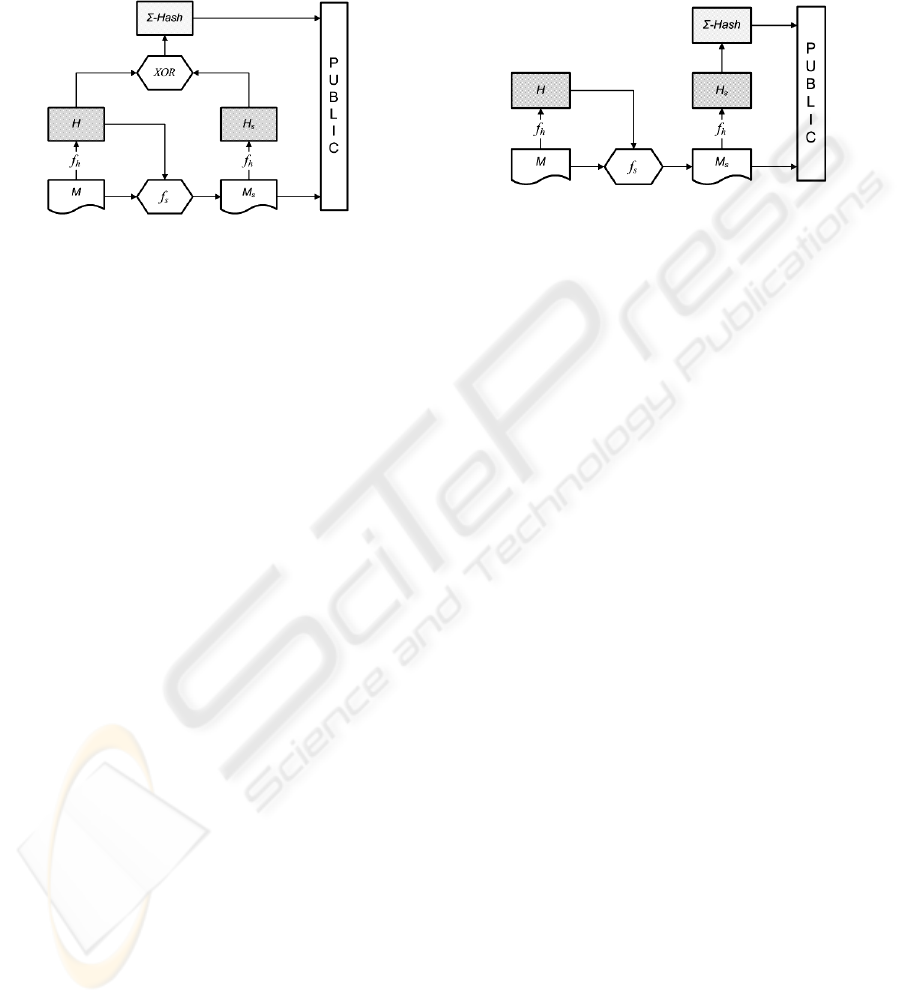
4 THE Σ-HASH SCHEME

The proposed scheme combines Steganography and

hash functions in order to improve the collision

resistance of the latter. In this section we will

describe in detail the proposed method.

Figure 1: Σ-Hash public mode.

4.1 Hashing and Verifying

Let M denote the original message that will be Σ-

Hashed. During the first step M is hashed using any

hashing algorithm f

, to produce the hash value H:

(M) = H

(1)

In the second step we embed the hash value H to

M. This can be done by using any known

steganographic algorithm f

. The stego-key for the

embedding process will be the hash value H that was

produced in the first step. The output of this step will

be a stego-object called M

as follows:

(M, H, H) = M

(2)

By choosing H as a key we eliminate the need

for a key exchange and maintenance, as the hash

value will be exchanged anyway. Furthermore, the

steganographic process ensures that the secret

message, in our case the hash value, will be spread

across the original message, regardless of its size

and without affecting its appearance and

functionality. Thus, the original object will remain

functional, regardless of the embedded message.

In the third step the stego-object M

is hashed:

) = H

(3)

We have now computed two different hash values

for seemingly the same object. The first one, H, is

the usual hash value, while the second one, H

, is

computed over an alternate version of the original

object, which contains a secret message, embedded

to it using steganography. The final hash value that

will be used is produced by XOR-ing H and H

Σ-Hash = H XOR H

(4)

Σ-Hash is distributed along with the stego-object

. Figure 1 depicts how this public mode of Σ-

Hash functions. Alternatively, a user may choose to

keep H private and only publish H

. In this case:

Σ-Hash = H

(5)

This private mode, viewed in

Figure 2, can be used

from the author of M, to monitor possible attempts

for collision attacks.

Figure 2: Σ-Hash private mode.

In order to verify the validity of the given hash

functions in terms of ensuring that there is no

attempt for collision attack, three steps should be

followed. Firstly, the given object, M

is hashed in

order to produce H

’ which is XOR-ed with Σ-Hash:

) = H

’

H’ = Σ-Hash XOR H

’

(6)

In the case of the private mode there is no need for

XOR-ing as H’ is already known to be equal to H

and kept private. As we mentioned in the previous

section H’ is used as the key for embedding the key

H to M. Thus, in order to retrieve H, which is stored

as a secret message using steganography, the inverse

steganographic function f

-1

is performed, using H’

as the stego-key:

-1

, H’) = H

(7)

Evidently, H’ should be equal with H, otherwise a

collision attack has been attempted.

4.2 Attacking Σ-Hash

We consider an attacker that wishes to attack Σ-Hash

in terms of collision resistance. Initially two choices

exist: find a collision for the hash of M or for the

hash of M

. In any case this would mean that M’ or

’ should be found so that:

H’ = f

(M’) = f

(M) = H

(8)

’ = f

’) = f

) = H

(9)

Considering the first choice, an attacker

computes M’ that produces the same hash value with

M. In this case, embedding H to M’ would produce a

significantly different stego-object M

’ ≠ M

. Robust

steganographic algorithms ensure that the hidden

data are not embedded into a specific area of the

cover object but instead are equally and randomly

spread into it. Thus, even slight variations in the

USING STEGANOGRAPHY TO IMPROVE HASH FUNCTIONS’ COLLISION RESISTANCE

339

contents of the cover object can produce different

stego-objects. The hash value of a different stego-

object M

’ would be different from H

and so would

be the final Σ-Hash value.

We argue here that a steganographic algorithm

fed with the same key and secret message but

slightly different input should produce alternate

outputs. In detail, inputs should different

significantly enough to be regarded as two separate

objects. If significant bits in cover objects are

different then steganography will produce different

outputs. Especially in text based steganography,

where two different cover objects are most likely

expected to also vary in length, the stego-object will

always be different. This fact also ensures that H

will also be different from H since M

is similarly

significantly different from M.

Similarly, an attacker may choose to find a

collision for H

by carefully choosing a different

stego-object M

’ so that: f

’) = H

. In that case

the inverse steganographic operation on M

’ will

give off a different secret message than the expected

hash value H. As the stego-object will be different

from the original one, the steganographic algorithm

will fail to provide the original hidden message.

Evidently, an attacker should be able to

overcome the difficulties set by steganography in

order to successfully attack Σ-Hash. Efficient

steganographic algorithms ensure that alterations to

cover-objects result in different stego-objects and

alterations to stego-objects make original hidden

messages impossible to retrieve. An attacker would

have to find a collision for H that also produces the

same stego-object M

, something that is considered

hard, having in mind the attacks we described in

section 2. It should also be mentioned that it is hard

even to extract M from M

as most steganographic

functions are not reversible.

4.3 Applications

Naturally, Σ-Hash can be used to enforce hash

function security. Its use can be applied to all known

applications of hashing algorithms as long as the

verification process is altered to match the one

required by Σ-Hash. As we have already mentioned,

Σ-Hash was originally designed as a solution to

source code tampering. An attacker able to modify

the source code will also be able to modify the hash

that will be used to verify its integrity. However, if

Σ-Hash is used, the attacker will not be able to

successfully compute the new Σ-Hash value as he

does not have knowledge of the cover object. In

detail, the attacker can only alter the stego object as

is only published. Suppose that he has also found

a collision for H

. When a user will try to verify Σ-

Hash, he will not be able to extract the correct

information from M

, and thus verification will fail.

5 REMARKS

In this paper we introduced Σ-Hash, a novel mode of

operation for hashing algorithms that uses

steganography to achieve better collision resistance.

We presented the details of our scheme, which can

be used with any existing or future hash function,

and analyzed how collisions are avoided.

Currently we are working on a proof of concept

implementation of Σ-Hash that will enable us to

experiment with further applications. We have

demonstrated that our scheme can be used to avoid

source code tampering, or phishing attacks. We

intend to present further applications of Σ-Hash,

using a real world implementation with commonly

used hash algorithms. Finally, we will provide

suggestions for specific steganographic algorithms

which are optimal for using with Σ-Hash.

REFERENCES

NIST, 1995. Secure hash standard. Federal Information

Processing Standard, FIPS-180-1.

R. Rivest, 1992. The MD5 Message-Digest Algorithm.

RFC 1321, IETF.

X. Y. Wang, 1997. The Collision attack on SHA-0. In

Chinese, to appear on www.infosec.edu.cn, 1997.

R.C. Merkle, 1989. A Certified Digital Signature. In

Advances in Cryptology - CRYPTO '89. Springer-

Verlag.

I. Damgård, 1989. A Design Principle for Hash Functions.

In Advances in Cryptology - CRYPTO '89. Springer-

Verlag.

S. M. Bellovin and E. K. Rescorla, 2005. Deploying a

New Hash Algorithm. In NIST Hash Function

Workshop.

S. Halevi and H. Krawczyk, 2005. Strengthening Digital

Signatures via Randomized Hashing, Internet Draft,

IETF.

E. Biham, R. Chen, A. Joux, P. Carribault, W. Jalby and

C. Lemuet, 2005. Collisions in SHA-0 and Reduced

SHA-1. In Advances in Cryptology–Eurocrypt’05.

Springer-Verlag.

X. Wang, D. Feng, X. Lai, and H. Yu, 2004. Collisions for

hash functions md4, md5, haval-128 and ripemd.

Cryptology ePrint Archive, Report 2004/199.

Available at: http://eprint.iacr.org/

B. den Boer and A. Bosselaers, 1993, Collisions for the

Compression Function of MD5. Advances in

Cryptology–Eurocrypt’03. Springer-Verlag.

X. Wang, Y. Yin, H. Yu, 2005. Finding Collisions in the

Full SHA-1. In Advances in Cryptology - CRYPTO '05.

M. Bellare, T. Kohno, 2004. Hash Function Balance and

its Impact on Birthday Attacks. In Advances in

Cryptology-EUROCRYPT 04. Springer-Verlag.

SECRYPT 2007 - International Conference on Security and Cryptography

340