
AN INSERTION STRATEGY FOR A TWO-DIMENSIONAL
SPATIAL ACCESS METHOD
Wendy Osborn
Department of Mathematics and Computer Science, University of Lethbridge, Lethbridge, Alberta, Canada, T1K 3M4
Ken Barker
Department of Computer Science, University of Calgary, Calgary, Alberta, Canada, T2N 1N4
Keywords:
Spatial access methods, multidimensional, hierarchical, data structures, performance.
Abstract:
This paper presents the 2DR-tree, a novel approach for accessing spatial data. The 2DR-tree uses nodes
that are the same dimensionality as the data space. All spatial relationships between objects are preserved.
A validity rule ensures that every node preserves the spatial relationships among its objects. The proposed
insertion strategy adds a new object by recursively partitioning the space occupied by a set of objects. A
performance evaluation shows the advantages of the 2DR-tree and identifies issues for future consideration.
1 INTRODUCTION
A spatial database contains a large collection of ob-
jects that are located in multidimensional space. An
important research issue in spatial databases is the ef-
ficient retrieval of objects based on location, using
spatial access methods (SAMs).
No n-dimensional to one-dimensional mapping of
spatial data exists that preserves all spatial relation-
ships between objects (Gaede and G
¨
unther, 1998).
However, SAMs use approaches that are intended for
alphanumeric data. This leads to a one-dimensional
spatial organization of objects. This also leads to un-
necessary searching within a node and the data struc-
ture as a whole, because the only option is a linear
search of a node in its entirety. It is not possible to
search only part of a node.
This paper describes a portion of our work on
a new hierarchical SAM to alleviate this limitation.
The 2DR-tree fits the existing object space by using
nodes of the same dimensionality. Therefore, two-
dimensional nodes are used to index objects in two-
dimensional space. Objects in each node are orga-
nized using a validity rule that preserves all spatial re-
lationships. This strategy allows the 2DR-tree to sup-
port non-linear searching strategies. We expect that
this strategy will reduce the amount of searching that
is performed in a node. In addition, overcoverage and
overlap will also be reduced.
2 RELATED WORK
Many approaches for indexing objects based on lo-
cation are proposed in the literature (see (Gaede and
G
¨
unther, 1998; Samet, 1990; Shekhar and Chawla,
2003) for surveys). These approaches are classi-
fied into three categories (Gaede and G
¨
unther, 1998):
main memory methods, point access methods and
spatial access methods (SAMs). Many important
strategies are proposed in all categories. We focus on
SAMs, since our work is in this category.
SAMs provide uniform access to both point and
object data. Also, they remain height-balanced in the
presence of a dynamic object set. Many SAMs are
proposed in the literature (Guttman, 1984; Beckmann
et al., 1990; Berchtold et al., 1996; Kamel and Falout-
sos, 1994; Sellis et al., 1987; Orenstein and Merrett,
1984; Koudas, 2000). They can be classified (Gaede
and G
¨
unther, 1998) into approximation, clipping, and
mapping methods.
Approximation methods store a hierarchy of ap-
proximations of both objects and the space occu-
pied by subsets of objects. Since the space is not
partitioned, approximations can overlap. Many ap-
proximation methods are proposed, including the R-
tree (Guttman, 1984), the R
∗
-tree (Beckmann et al.,
1990) and the X-tree (Berchtold et al., 1996). Clip-
ping methods, such as the R
+
-tree (Sellis et al.,
1987), partition an object into parts so that over-
295
Osborn W. and Barker K. (2007).
AN INSERTION STRATEGY FOR A TWO-DIMENSIONAL SPATIAL ACCESS METHOD.
In Proceedings of the Ninth International Conference on Enterprise Information Systems - DISI, pages 295-300
DOI: 10.5220/0002408002950300
Copyright
c
SciTePress
lap is avoided. Mapping methods map objects in n-
dimensional space into a one-dimensional order. The
objects are then stored and retrieved using an access
method such as a B
+
-tree (Comer, 1979). Approaches
that use mapping include Z-ordering (Orenstein and
Merrett, 1984), the Hilbert R-tree (Kamel and Falout-
sos, 1994), and the Filter tree (Koudas, 2000).
No n-dimensional to one-dimensional mapping
of spatial data exists that preserves all spatial re-
lationships between objects (Gaede and G
¨
unther,
1998). A limitation to hierarchical SAMs is their
one-dimensional structure. This forces objects in n-
dimensional space into a one-dimensional ordering,
which results in the loss of spatial relationships. This
leads to inefficient searching, both within a node and
the structure as a whole, because the only option is a
linear search of a node in its entirety. Mapping meth-
ods do provide a one-dimensional ordering of objects,
but they cannot maintain all spatial relationships.
3 THE 2DR-TREE
The 2DR-tree is an approximation SAM that uses
nodes that are two-dimensional in structure to orga-
nize approximations for objects and the space oc-
cupied by objects. In every node, an approxima-
tion is stored in an appropriate location with re-
spect to all other approximations in the node. Using
two-dimensional nodes allows approximations to be
placed so that spatial relationships are preserved. We
present the 2DR-tree and define key concepts below.
3.1 Preliminaries
The 2DR-tree uses a minimum bounding rectangle
(MBR) for approximating an object and the space oc-
cupied by a subset of objects. An MBR is the mini-
mum extent along both the x-axis and the y-axis that
encompasses an object in a leaf node, and a subset of
MBRs in a non-leaf node. The centroid of an MBR
are the co-ordinates (i, j) of its centre.
The supported spatial relationships are north, east,
south, west, northeast, northwest, southeast, and
southwest. A spatial relationship is determined by
comparing the centroids between two MBRs. This
leads to a smaller set than that in (Papadias et al.,
1996), but we feel this simpler technique covers all
required cases.
The coverage of an MBR is the total area covered
by the rectangle. The coverage of a tree is the total
coverage of all MBRs in the tree. The overcoverage
of an MBR is the area of the whitespace within a rect-
angle. The overcoverage of a tree is the total overcov-
m9
m8
m5
m3
m1
m2
m4
p9
p5
m3
m2
p9
m7
m4
m5
m8
m9
m1
p5
m7
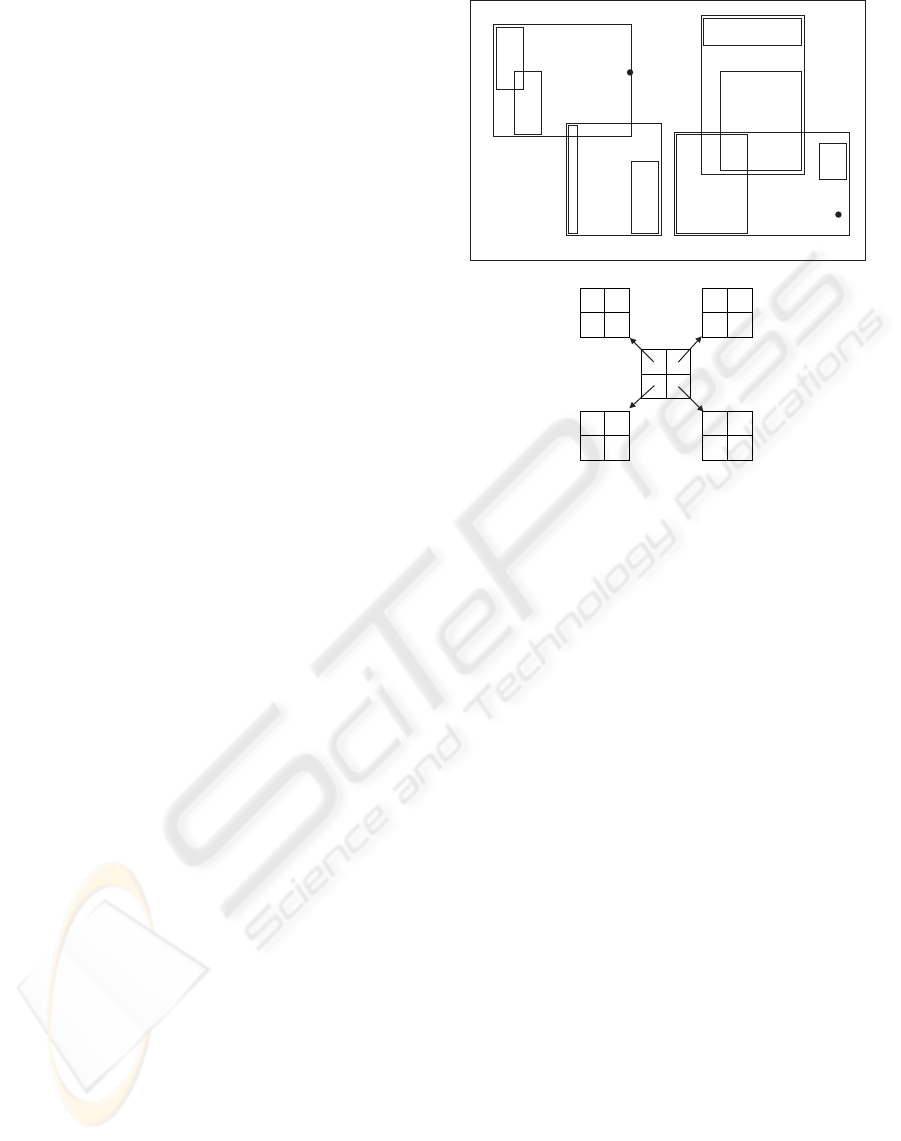
Figure 1: Order 4*4 2DR-tree.
erage of all MBRs in the tree. The overlap of a tree is
the total overlap between all pairs of MBRs.
For each node N, X is the number of indexed lo-
cations along the x-axis, and Y is the number of in-
dexed locations along the y-axis. The order of N is
O = X ∗ Y. All nodes in a 2DR-tree have the same
order. Therefore, the order of a 2DR-tree is the order
of its nodes. Each location (i, j) in node N stores:
(MBR
(i, j)
, ptr
(i, j)
)
where MBR
(i, j)
is an MBR and ptr
(i, j)
is a pointer. In
a leaf node, MBR
(i, j)
encloses an object and ptr
(i, j)
references the object on secondary storage. In a non-
leaf node, MBR
(i, j)
encloses all MBRs in the subtree
referenced by ptr
(i, j)
.
A node space is the area of space occupied by a
set of objects. This is equal to the MBR that encloses
the objects. A node region (lx, hx, ly, hy) is a two-
dimensional subset of (x, y) index locations in a node.
The index values lx and hx are the lower and upper
bounds of the node region along the x-axis. The in-
dex values ly and hy are the lower and upper bounds
of the node region along the y-axis.
3.2 Node Validity
To employ different searching strategies, the spa-
tial relationships between MBRs in each node must
be preserved. For each location N
(i, j)
, i = 0. . . (X −
ICEIS 2007 - International Conference on Enterprise Information Systems
296

1), j = 0. . . (Y − 1) in node N, if N
(i, j)
contains
MBR
(i, j)
,
• Location N
(k,l)
, k = (i + 1). . . (X − 1), l = 0. . . j
contains MBR
(k,l)
whose centroid is southeast of
the centroid for MBR
(i, j)
,
• Location N
(k,l)
, k = (i + 1) . . . (X − 1), l = ( j +
1). . . (Y − 1) contains MBR
(k,l)
whose centroid is
northeast of the centroid for MBR
(i, j)
, and
• Location N
(k,l)
, k = 0. . . i, l = ( j + 1) . . . (Y − 1)
contains MBR
(k,l)
whose centroid is northwest of
the centroid for MBR
(i, j)
.
Figure 1 shows an order 2*2 2DR-tree that pre-
serves all spatial relationships for the given data set
(from (Gaede and G
¨
unther, 1998)). Beginning with
the leaf node descending from root location (0, 0), the
centroid for m3 is located southeast of the centroid so
m3 is located east of m4 in the node (m4,m3). In node
(m5,p5,m8), p5 is located southeast of the centroid for
m5, and the centroid for m8 is located northeast of the
centroid for m5 and northwest of p5. Therefore, p5 is
stored east of m5 while m8 is stored northeast of m5
and north of p5. Spatial relationships are also main-
tained in nodes (m7,m9), (m2,m1,p9), and the root
node.
4 2DR-TREE INSERTION
The 2DR-tree insertion strategy has five stages: 1)
search for an appropriate leaf node, 2) search for the
appropriate location within the leaf node, 3) place the
new object with respect to any objects remaining in
the node so that spatial relationships are maintained,
4) attempt to put back the objects that were removed
so that spatial relationships are maintained – if not
possible, then a split is performed, and 5) perform an
update of the insertion path. The first four stages are
detailed here.
4.1 Leaf Node Search
An appropriate leaf node is found for new object
MBR
n
by applying a greedy search to each node on
the insertion path. Each chosen node contains an
MBR that requires either a minimal or the least area
increase necessary to include the new object. The
greedy search finds this MBR along a path of decreas-
ing area increases. The most optimal MBR may not
be found, but the number involved in the search is
reduced. This is because the approximations in the
node are now organized, and other search strategies
can now be applied.
Beginning at location (0, 0), each approximation
in location (i, j) on the search path is compared with
(i, j + 1),(i + 1, j + 1) and (i + 1, j). If the MBR at
(i, j) has the smallest area increase, the search termi-
nates in the node and continues in the corresponding
subtree. Otherwise, the search continues in the direc-
tion that contains an MBR with the smallest area in-
crease. This is repeated at each level of the tree, until
a leaf node is reached.
4.2 Object Location Search
After a leaf node is found, a location for MBR
n
is
found within the node by performing a recursive par-
tition of the node space NS that corresponds to the leaf
node. For each recursive stage, two steps take place.
First, the node space is partitioned into two equal sub-
spaces through the dimension with the longest extent.
Second, a node region that corresponds to each sub-
space is identified. The subspace (and corresponding
node region) that contains MBR
n
is selected for fur-
ther partitioning, while the node region correspond-
ing to the other subspace is removed from the node
and will be put back after MBR
n
is inserted.
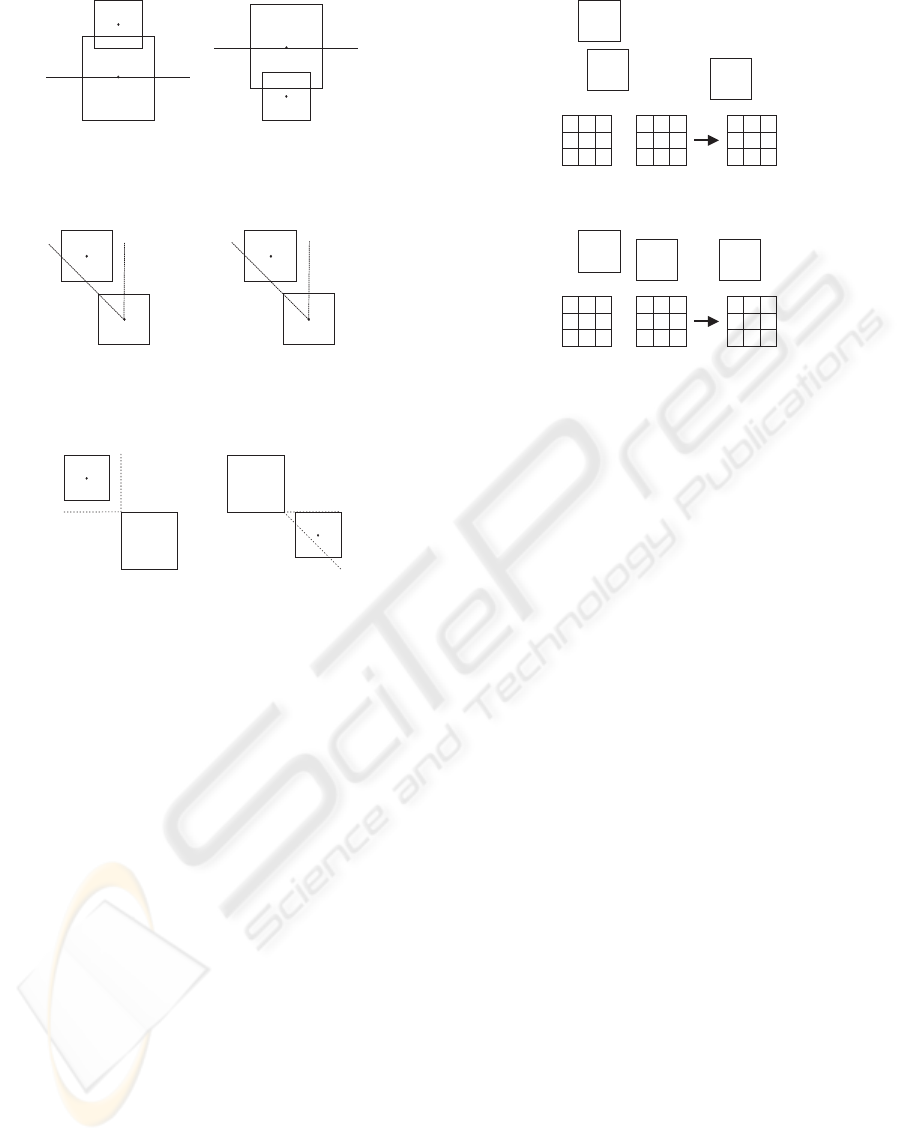
Figure 2 shows partitioning for the north and south
cases, and how the new object relates to the partition.
In Figure 2a, the new object N is located north of the
partition. In Figure 2b, N is located south of the par-
tition. In these cases, the north or south subspace re-
spectively is chosen for further partitioning.
Recursive partitioning continues until either one
MBR remains in the node (MBR
r
), or multiple objects
exist and MBR
n
has some specific spatial relationship
with those objects.
4.3 New Object Placement
After removing subsets of objects, MBR
n
is inserted
with respect to the remaining object(s) to ensure that
all spatial relationships are maintained. We present
the cases for insertion relative to one MBR, followed
by insertion relative to multiple MBRs.
The cases for insertion MBR
n
relative to one
remaining approximation, MBR
r
are listed below.
MBR
r
is located at (i, j).
North Insert. MBR
n
is located northwest of MBR
r
and the slope of a line between their centroids is less
than −1. MBR
n
is inserted in location (i, j+ 1). This
is depicted in Figure 3a.
North Swap Insert. MBR
n
is located southeast of
MBR
r
and the slope of a line between their centroids
is less than −1. MBR
n
is swapped with MBR
r
and
MBR
r
is inserted in location (i, j + 1). This is de-
picted in Figure 3b.
AN INSERTION STRATEGY FOR A TWO-DIMENSIONAL SPATIAL ACCESS METHOD
297
MBR
n
NS
MBR
n
NS
a. North b. South
Figure 2: Partitioning Cases for North and South.
MBR
n
MBR
r
MBR
n
MBR
r
a. North Insert b. North Swap Insert
Figure 3: Single Object Cases for North Inserts.
MBR
n
NS
MBR
n
NS
a. North Insert b. East Insert
Figure 4: Multiple Object Cases for North and East.
East Insert. MBR
n
is located southeast of MBR
r
and
the slope of a line between their centroids is greater
than −1. MBR
n
is inserted in (i+ 1, j).
East Swap Insert. MBR
n
is located northwest of
MBR
r
and the slope of a line between their centroids
is greater than −1. MBR
n
is swapped with MBR
r
and
MBR
r
is inserted in (i+ 1, j).
Northeast Insert. MBR
n
is located northeast of
MBR
r
. MBR
n
is inserted in (i+ 1, j + 1).
Northeast Swap Insert. MBR
r
is located northeast of
MBR
n
. MBR
n
is swapped with MBR
r
and MBR
r
is
inserted in (i+ 1, j + 1).
The multiple object cases identify situations
where MBR
n
has certain spatial relationships rela-
tive to all remaining approximations in the node.
For all cases, the remaining approximations occupy
node space NS, which corresponds to node region
(lx
rns
, hx
rns
, ly
rns
, hy
rns
).
North Insert. MBR
n
is located northwest of NS, and
the slope of a line between their centroids is less than
−1. MBR
n
is inserted in location (lx
rns
, hy
rns
+ 1).
This is depicted in Figure 4a.
East Insert. MBR
n
is located southeast of NS, and the
slope of a line between their centroids is greater than
1
2
3
1
3
2 2
3
1
a. East, No Overlap
1
23
1
3
2 2
3
1
b. East, Overlap
Figure 5: Node Restore for East Cases.
−1. MBR
n
is inserted in location (hx
rns
+ 1, ly
rns
).
This is depicted in Figure 4b.
Northeast Insert. MBR
n
is located northeast of NS.
MBR
n
is inserted in location (hx
rns
+ 1, hy
rns
+ 1).
Northeast Swap Insert. MBR
n
is located southwest
of NS. The node region is shifted to the northeast
(i.e. over one column and up one row), and MBR
n
is
inserted into the original (lx
rns
, ly
rns
) location.
4.4 Restoring the Leaf Node
After MBR
n
is inserted, any removed node regions
are restored in the reverse order of their removal. Af-
ter replacing each node region, a validity test is per-
formed. The final result is either a completely re-
stored node, or a set of nodes if a split is required.
Each removed node region has a direction of
north, south, east, or west, depending on which side
of the partition its corresponding node space was on.
This direction is used to restore the node region rel-
ative to (lx
rns
, hx
rns
, ly
rns
, hy
rns
). When MBR
n
is in-
serted, one or both of the upper node region bound-
aries hx
rns
and hy
rns
are increased. When this in-
crease occurs, potential overlap problems arise be-
tween the node region (lx
rns
, hx
rns
, ly
rns
, hy
rns
) and
some removed node regions, namely the east and
north node regions. Therefore, the resulting cases
are north, north with overlap, east, east with overlap,
south and west.
The east and east with overlap cases are depicted
in Figure 5. When east node region (lx
e
, hx
e
, ly
e
, hy
e
)
does not overlap with (lx
rns
, hx
rns
, ly
rns
, hy
rns
), it is
put back into its original location. However, when the
east node region (lx
e
, hx
e
, ly
e
, hy
e
) does overlaps with
ICEIS 2007 - International Conference on Enterprise Information Systems
298
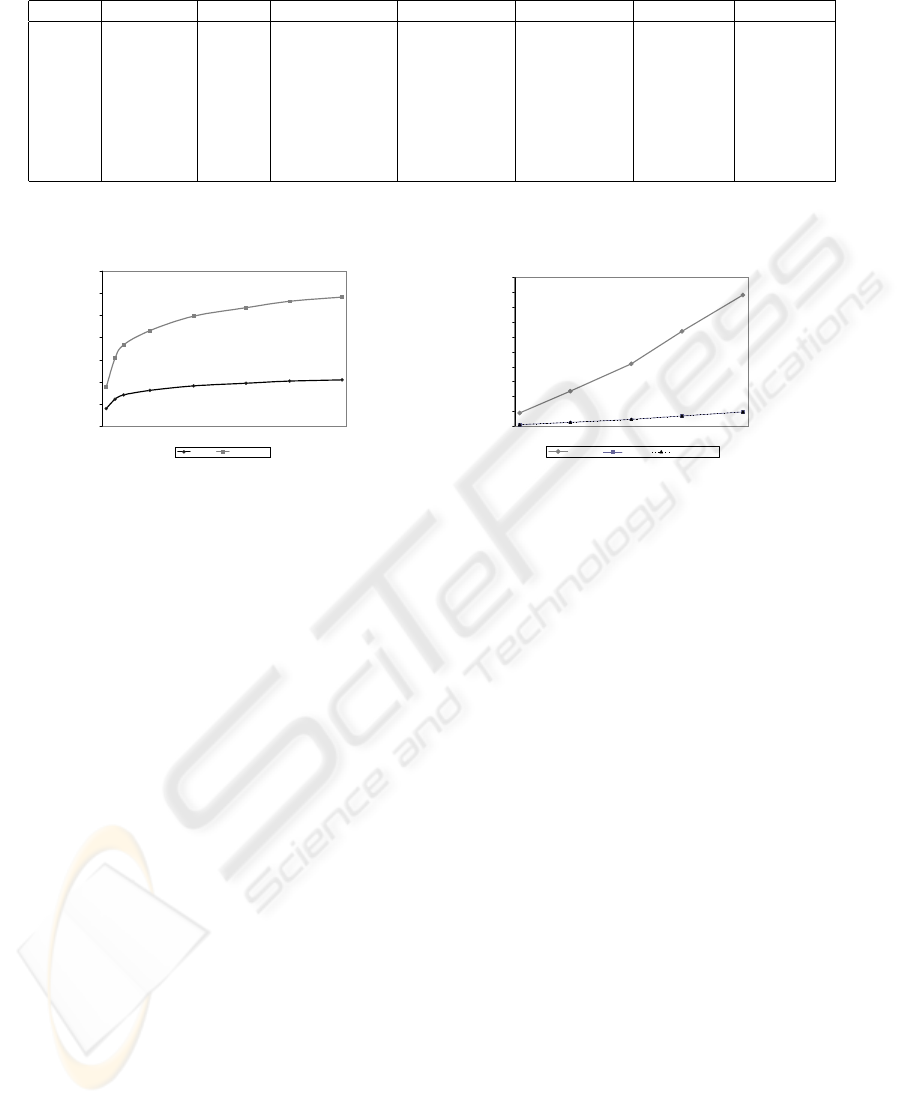
Table 1: Averages for Varying Object Set Size.
#Obj #Nodes Height Coverage Overcov Overlap #Seeks/Ins #Splits/Ins
100 127.97 8.10 128,906.74 15,801.81 13,070.12 17.82 1.04
500 654.06 12.31 1,233,595.22 138,768.90 129,630.80 30.74 1.12
1,000 1,312.53 14.19 3,232,169.34 355,257.04 340,590.69 36.74 1.13
2,000 2,619,52 16.23 8,784,155.25 959,547.75 935,355.26 43.11 1.13
4,000 5,244.69 18.26 23,448,427.79 2,535,300.42 2,494,116.09 49.59 1.13
6,000 7,867.63 19.47 41,887,513.70 4,525,004.07 4,465,319.16 53.43 1.13
8,000 10,470.28 20.44 63,752,968.22 6,862,775.80 6,792,707.51 56.28 1.13
10,000 13.077.67 21.00 88,158,132.24 9,517,985.63 9,432,726.01 58.20 1.13
#Object vs. Height and #Seeks/Ins
1000
1000
2000
4000
6000
8000
10000
500
100
2000
10000
8000
6000
4000
500
100
0
10
20
30
40
50
60
70
#Objects
Height #Seeks/Ins
#Objects vs. Coverage/Overcoverage/Overlap
10000
8000
6000
4000
2000
2000
4000
6000
8000
10000
0
10
20
30
40
50
60
70
80
90
100
Millions
#Objects
Coverage Overlap Overcoverage
a. #Objects vs. Height and #Seeks/Insert b. #Objects vs. Coverage/Overlap/Overcoverage
Figure 6: Affect of Object Set Size on Various Parameters.
(lx
rns
, hx
rns
, ly
rns
, hy
rns
), it is shifted one column east
from its original position before it is put back. The
other cases are handled similarly.
To handle overflow and node invalidity, different
splitting strategies are used. One strategy is the reduc-
tion split, which takes advantage of the node regions
that are removed from the node. Each node region
that cannot be put back is assigned to its own node.
5 PERFORMANCE EVALUATION
The preliminary performance evaluation observes the
behaviour of the 2DR-tree for different object set
sizes and distributions. We created object sets that
contain between 100 and 10,000 equal-sized squares.
With between 51-53% overlap, each set covers 67-
75% of the space.
Each test run constructs 1000 trees using random
sorts of the object set. The tree height, number of
nodes, average space utilization, coverage, overcov-
erage, overlap, average number of disk accesses per
insertion, and the average number of splits per in-
sertion are recorded. Each disk access retrieves one
node. We assume that each page from secondary stor-
age stores the information for one node, independent
of node size. We also assume that with the exception
of the root node and new nodes produced from a split,
each node is retrieved every time it is read. In the lat-
ter case, the MBRs required for updating are gener-
ated immediately after creating the node so retrieving
new nodes resulting from a split is not required.
We evaluate the insertion algorithm using the fol-
lowing sets of test runs: 1) varying the number of ob-
jects between 100 and 10000, using a 5x5 node size
and uniform distribution, 2) varying the data distri-
bution between uniform and exponential, using 500
objects and a 5x5 node size.
5.1 Results and Discussion
Table 1 shows the averages for each run when vary-
ing the number of objects inserted into the 2DR-tree.
The average number of seeks per insert is less than
three times the average tree height in all cases. This
includes the number required to find the appropriate
leaf node so updating takes the remaining seeks. The
average number of seeks for updating is more than
one times the average tree height due to the average of
approximately one split per insertion occurring. This
is significant since splits can be triggered by many sit-
uations in the 2DR-tree. The results show that splits
are not a significant factor for 2DR-tree insertion.
Figure 6a shows the effect of the number of ob-
AN INSERTION STRATEGY FOR A TWO-DIMENSIONAL SPATIAL ACCESS METHOD
299

Table 2: Averages for Varying Distribution.
Distribution #Nodes Height Coverage Overcov Overlap #Seeks/Ins #Splits/Ins
Uniform 654.06 12.31 1,233,595.22 138,768.90 129,630.80 30.74 1.12
Exponential 652.63 12.31 638,430.98 64,157.58 67,130.08 30.71 1.10
jects inserted on the tree height, and the average num-
ber of disk accesses required for inserting an object.
Initially, the tree grows in height quickly but growth
slows significantly as more objects are inserted. The
same occurs for the number of disk accesses.
Figure 6b shows the effect of the number of ob-
jects inserted on the coverage, overlap and overcover-
age. Results show that the coverage increases linearly
as the number of objects increase. In addition, the
rate of increase in overlap and overcoverage is signif-
icantly lower as the number of objects increase. Cov-
erage includes the object coverage, while overlap and
overcoverage are only calculated for non-leaf nodes.
One reason for the lower growth in overlap and over-
coverage is the ability of the 2DR-tree to “cluster”
objects located close together as the number of ob-
jects increase, which reduce both the overlap and the
wasted space in non-leaf approximations.
Table 2 shows the averages for each run when
varying the distribution of the data set. The results
show a significant difference in coverage, overcover-
age, and overlap. The surprising result is that when
indexing exponentially distributed data, the 2DR-
tree achieves significantly, almost 50%, lower cover-
age and overlap, and 54% lower overcoverage. The
height, number of nodes, and space utilization are not
a factor in this because they are not significantly dif-
ferent between the data distributions. After many in-
sertions, “chains” that consist of many non-leaf nodes
that lead to one node with few objects - possibly one -
start to appear. An advantage to chains is that outliers
are separated from a cluster of objects, which reduces
the coverage, overcoverage, and overlap of MBRs.
6 CONCLUSION
This paper presents work on the 2DR-tree, which pre-
serves spatial relationships between all objects by us-
ing nodes that are the same dimensionality as the ob-
ject set. This structure supports non-linear search
strategies. We present the insertion strategy and some
preliminary evaluation results. The results show that
the 2DR-tree is ideal for larger objects sets with re-
spect to tree height. The average number of disk ac-
cesses and split per insert are reasonable. In addi-
tion, it is ideal for a dynamic skewed data set, which
achieves lower coverage, overcoverage, and overlap
than a dynamic, uniformly distributed data set.
Some research directions include: 1) a perfor-
mance evaluation versus other proposed SAMs; 2)
improving the average space utilization, which is very
low; 3) developing an algorithm for bottom-up tree
construction applicable to static data sets; 4) extend-
ing the 2DR-tree for three dimensions.
REFERENCES
Beckmann, N., Kriegel, H.-P., Schneider, R., and Seeger,
B. (1990). The R
∗
-tree: an efficient and robust access
method for points and rectangles. In Proceedings of
the ACM SIGMOD International Conference on Man-
agement of Data, pages 322–31.
Berchtold, S., Keim, D., and Kriegel, H.-P. (1996). The X-
tree: An index structure for high-dimensional data. In
Proceedings of the 22nd International Conference on
Very Large Data Bases, pages 28–39.
Comer, D. (1979). The ubiquitous B-tree. ACM Computing
Surveys, 11:121–37.
Gaede, V. and G
¨
unther, O. (1998). Multidimensional access
methods. ACM Computing Surveys, 30:170–231.
Guttman, A. (1984). R-trees: a dynamic index structure
for spatial searching. In Proceedings of the ACM
SIGMOD International Conference on Management
of Data, pages 47–57.
Kamel, I. and Faloutsos, C. (1994). Hilbert R-tree: an im-
proved r-tree using fractals. In Proceedings of the 20th
International Conference on Very Large Data Bases,
pages 500–9.
Koudas, N. (2000). Indexing support for spatial joins. Data
and Knowledge Engineering, 34:99–124.
Orenstein, J. and Merrett, T. (1984). A class of data struc-
tures for associative searching. In Proceedings of the
Third ACM SIGACT-SIGMOD Symposium on Princi-
ples of Database Systems, pages 181–90.
Papadias, D., Egenhofer, M., and Sharma, J. (1996). Hier-
archical reasoning about direction relations. In Pro-
ceedings of the 4th ACM-GIS.
Samet, H. (1990). The design and analysis of spatial data
structures. Addison-Wesley.
Sellis, T., Roussopoulos, N., and Faloutsos, C. (1987). The
R
+
-tree: a dynamic index for multi-dimensional ob-
jects. In Proceedings of the 13th International Con-
ference on Very Large Data Bases.
Shekhar, S. and Chawla, S. (2003). Spatial databases: a
tour. Prentice Hall.
ICEIS 2007 - International Conference on Enterprise Information Systems
300
