
USE OF REQUIREMENT STABILITY IN OPTIMIZING
ITERATIVE DEVELOPMENT PROCESSES
Gilberto Matos
Siemens Corporate Research, 755 College Rd East, Princeton, NJ, USA
Keywords: Iterative Process, Agile Development, Requirement Stability, Simulation, Optimization.
Abstract: Unstable requirements are widely understood as being a common cause of problems in delivering desired
software functionality on time and within budget. Requirement volatility manifests itself through various
symptoms, including scope creep, rejected feature implementations, and late discovery of non-functional
requirements. Iterative processes use cycles of development and feedback to create an environment where
requirements can be evolved to better address the user’s needs. Agile development methods are based on the
assumption that the most valuable feedback comes from customers reviewing a live demo of the system
being developed. The duration of an iteration generally determines the frequency of such reviews, and we
are interested in understanding its impact on the development process. We developed a discrete simulation
model of iterative development processes, and use it to evaluate process efficiency. By simulating the
process for different iteration durations and initial requirement stability levels, we show that efficiency in
iterative development processes depends on how well the iteration duration is adjusted to the initial
requirement stability. We also propose a method for actively evaluating requirement stability, and using that
information to adjust the review frequency during the execution of a development project.
1 INTRODUCTION
Requirement engineering is increasingly a critical
aspect of successful software development. One of
the major drivers is the need for detailed and stable
requirements for projects which are outsourced to
reduce development cost. Yet, it has been well-
established that the requirements are rarely known or
stable before development begins. Normally,
requirements change throughout the development of
a software project, often up until the very end. Final
requirement stability is often dictated mainly by the
decision to cut off further changes and postpone
them for later releases.
Iterative development methods offer an effective
approach for dealing with requirement changes, due
to the repeated opportunities for reviewing
deliverables and reprioritizing the remaining planned
features. The duration of an iteration is based on a
trade-off between the need for concentrating the
developers on doing the work, and having the work
reviewed by customers at the end of iteration.
Multiple authors (Cohn, 2004)(Schwaber, 2001)
recommend using the same iteration length
throughout the development process, mainly because
that sets up a rhythm for the project conduct and
particularly for inter-team interactions. While this
concept serves the needs of time and resource
management, the requirement volatility in the early
stages of a project requires more frequent feedback.
Relationship between requirement stability and
project success is mostly studied in the narrow sense
of changing customer requests (Fayad, 2001)(Jayed,
2004)(Jones, 1998). The generally accepted rate of
requirement change in mature projects is 2-3% per
month from customer requests and marketplace
changes (Jones, 1998). This rate implies that at least
a third of the requirements for an application
changes over the course of a year.
In iterative development processes, some
development activities start very early, even before
all of the requirements are agreed upon. Our
previous research activities explored how iterative
and agile development processes can be applied in
the prototyping context, with the explicit goal of
identifying and developing product requirements.
(Hwong, 2007)(Song, 2005). Requirement stability
or volatility in these situations also reflects the
developers’ incomplete understanding of the domain
or requirements, since the requirements may be
113
Matos G. (2007).
USE OF REQUIREMENT STABILITY IN OPTIMIZING ITERATIVE DEVELOPMENT PROCESSES.
In Proceedings of the Second International Conference on Evaluation of Novel Approaches to Software Engineering , pages 113-118
DOI: 10.5220/0002587101130118
Copyright
c
SciTePress

known to the client, but are not understood by the
development team. The requirement volatility in this
phase can be orders of magnitude larger than in
more mature projects.
We are interested in understanding how iteration
duration impacts the efficiency of development.
Having a longer iteration with less time spent on
fixed costs is an obvious way to increase efficiency.
We have seen long-running agile projects evolve to
shorten the time spent on the iteration wrap-up and
planning to increase output. On the other hand, we
have also taken part in several projects where short
iterations and significant review time had a valuable
impact on the project success by rapidly developing
a consensus about the requirements.
Quantitative simulations have been used in many
areas of software engineering (DeMarco,
2003)(Pfahl, 2000), to improve the understanding of
software development processes, and even attempt
to predict and optimize the release contents and
schedules. We developed a discrete model of
iterative software development processes. It
emphasizes the relationship between requirement
stability and effort needed to implement specific
work packages. We have used this model in Monte
Carlo simulations, assuming low requirement
stability. Our simulations indicate that shorter
iterations provide significant benefits to projects
with unstable or unclear requirements. We also
simulated several previously completed projects to
see how much their efficiency could have been
increased by changing the iteration duration.
The organization of this paper is as follows: first
we introduce the model that we use for impact of
requirement stability on iterative development, then
we describe the general simulation results. In the
next section we describe the findings from applying
the simulation to models of previously completed
projects. Finally we propose a way to use the
information about requirement stability in improving
the efficiency of iterative development processes.
2 SIMULATION MODEL OF
ITERATIVE DEVELOPMENT
Our simulation model represents the relationship
between development and requirement stability in
iterative development processes. The primary aspect
of iterative development used in this model is the
fixed length iteration with review of deliverables
only at the end. This model implies that the impact
of unstable requirements is only felt when the
deliverables are presented for a customer review.
Software development projects commonly start
with only a fuzzy idea of how much time and effort
a certain implementation will require. There are
multiple reasons for this, most of which are
requirement-related, and range from incompleteness
and inconsistency to the inherent instability due to
evolving or conflicting opinions of the stakeholders.
Requirement stability is closely correlated to the
successful implementation of a work package in the
allocated time and effort. The stability of
requirements depends on multiple factors, including
completeness, consistency, and maturity of the
requirements. It also reflects the consensus among
the stakeholders, because without their agreement,
the requirements are likely to change later. Finally,
we also use requirement stability to model the
development team’s knowledge and understanding
of the application domain.
Our simulation model uses work packages as
units of work. We assume that each work package
corresponds to a self-contained package of
requirements, that it can be completed in a single
iteration, and is sufficiently user-relevant to be
reliably reviewed by the customer at the end of the
iteration. Most agile development processes require
small user-relevant work packages (Beck,
1999)(Cohn, 2004)(Schwaber, 2001), so that the
user can accept or reject them at the iteration
reviews.
We need to define complexity and stability in a
way that is useful for quantitative Monte Carlo
simulation. The complexity will denote the effort
needed to implement a specific work package. We
will assume that the simulation uses the real
complexity values, as can be collected from project
time management at the end of an iteration. The
simulation uses the complexity of work packages
only for calculating the progress and results, and not
for scheduling the tasks into iterations, thus the
assumption of using the exact complexity of the
work packages does not affect the results.
The stability is also defined based on after-the-
fact measurements. We will define the stability of
the requirements for a specific work package as the
fraction of the development work on that package
that is accepted by the customer, exactly as
implemented and presented. This measure reflects
the completeness, consistency, unambiguousness,
and usability of the work package, as described by
the requirement specification. It can also be used to
denote the probability of requirement changes by
stakeholders, and to reflect the development team’s
ENASE 2007 - International Conference on Evaluation on Novel Approaches to Software Engineering
114

understanding of the problem and solution domain.
This definition of stability, based on misspent effort,
avoids the highly nonlinear relationship between
requirements and their implementation complexity.
Once a work package is implemented and
reviewed by the customer, the feedback to the
development team will increase the information
about the requirements for the rejected parts of the
work, thus resulting in higher stability for the next
implementation attempt. We model the increased
stability on reworked work packages as reducing
their volatility by half.
Similarly, consistency across the application and
the increased knowledge of the developers has a
stabilizing effect even on the requirements which
have not been worked on yet. We assume that the he
stability improvement for affected work packages is
the same as for the work packages worked on and
rejected, with their requirement volatility reduced by
half. The requirement impact is assigned randomly,
with a linear relationship between the total effort in
the iteration and the total of work packages that
benefit from the feedback. For the purposes of our
simulations, we assumed this impact ratio to be 3.
Depending on the application domain and the
similarity of the components of the application, this
ratio may vary widely. The important assumption of
our model is that it is unlikely to ever be close to 0,
since this would imply that no knowledge from any
work package would be relevant to others. .
Reduction in the assumed impact ratio reduces the
benefits of short iterations, without changing the
overall conclusions.
Here is a simple example of the execution of an
iteration: project consists of 10 work packages,
complexity of each package being 10 ideal time
units, with requirement stability 50%. If two work
packages are completed during an iteration and
reviewed by the customer, 50% of each will be
accepted, the remainder for these two work packages
will need to be reworked with a 75% stability. The
total complexity of the work performed is 20 units,
so another six work packages (60 units) will be
positively impacted, raising their stability to 75%.
Thus, at the start of next iteration, 2 work packages
are 50% complete, with 75% stability of remaining
work, 6 work packages have not been started, but
their requirement stability is also 75%, and 2 work
packages remain with 50% stability.
3 SIMULATION FOR SIMPLE
MODELS
We performed a number of simulations on the
model, keeping most parameters constant, and
varying only the iteration duration and the initial
requirement stability.
We assume a constant iteration cost, covering
for the iteration preparation, completion and review.
The initial iteration planning and the preparation for
delivery and presentation at the end of an iteration
will take some team members a day or two in
practice. This cost can be clearly seen if the
simulation is performed with the assumption of
stable requirements, where ideally all the
implementation effort is useful, and results in
accepted work packages. The percentage of useful
work in this situation is shown in the Figure 1. The
assumed fixed cost is .5 days per team member, so
50% efficiency is achieved with 1 day iterations,
while it reaches 97.5% for the 20 day iterations. In
this simple case, simulation results correspond to
analytically computable expected efficiency.
0.00%
20.00%
40.00%
60.00%
80.00%
100.00%
0 5 10 15 20 25
Iteration duration in days
Efficiency
Figure 1: Iteration efficiency depending on length.
Figure 2 shows the simulation results for 3
variations of iterative processes, showing accepted
features over time. The duration is tabulated in
multiples of a single short iteration, and the other
two processes use iterations which are double and
triple that length, respectively. The initial stability
assumed in this example is very low, so the first
iteration has very low productivity. After completing
a review in the first iteration, the improved
requirement stability enhances the productivity in
subsequent iterations.
The results of this simulation show that using
the shortest iteration brings the fastest improvements
to the development team productivity in the early
USE OF REQUIREMENT STABILITY IN OPTIMIZING ITERATIVE DEVELOPMENT PROCESSES
115
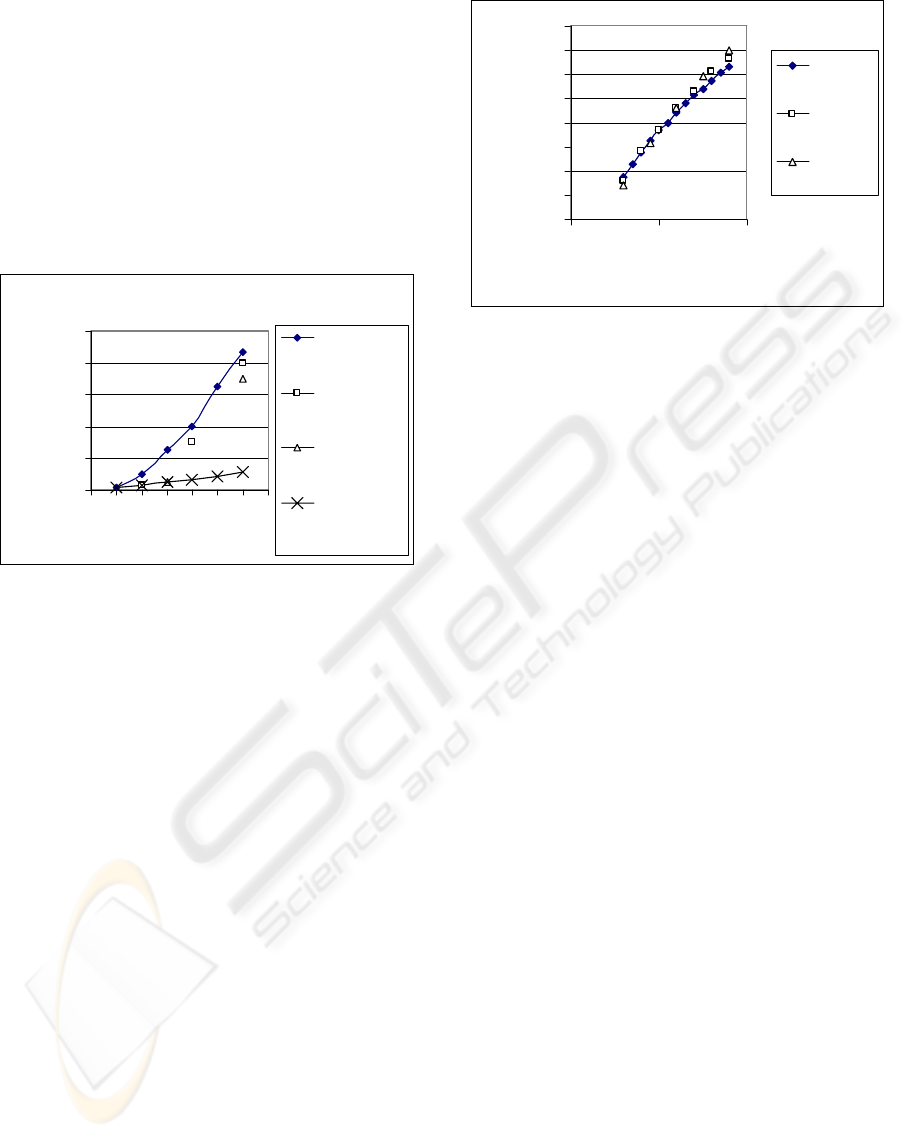
phases of projects with unstable requirements.
Intuitively, there are two reasons for this benefit:
less work on misunderstood requirements and more
work on requirements whose stability has benefited
from a review session at the end of the first short
iteration. The first iteration is the most wasteful one,
regardless of its duration. Unstable requirements
(undefined, misunderstood, lack of technology
expertise…) are the primary reason for this, and the
effect is that much of the development activity at
this point may eventually be rejected.
Initial development efficiency
0
200
400
600
800
1000
01234567
Time and effort
Completed
1 period
iteration
2 period
3 period
extrapolated
initial
iteration
Figure 2: Initial Efficiency starting with low stability.
The extrapolated line for results of initial iteration
of varying lengths, denoted by X’s, shows the effect
of very long iterations on projects with very unstable
requirements. While the short iteration process
approaches optimal efficiency with stable
requirements, the hypothetical process with 6 times
longer iteration has just gone through the process of
getting most of its deliverables rejected. The wasted
effort in the initial iteration is determined primarily
by the requirement volatility (low initial slope of the
curve), and duration of the iteration.
As the requirement stability increases, the shorter
iterations lose their advantage. Figure 3 shows the
progress for the same set of 3 simulated projects,
past the initial few iterations. The project with triple
length of iterations starts with lower output, due to
its lower efficiency with volatile requirements.
Efficiency of the longer iterations eventually leads to
higher overall productivity, primarily due to the
higher ratio of productive time in a longer iteration.
The point where longer transitions take over on the
efficiency graph is around the half-way point in
terms of completion of project. Since the
requirement started with low stability, the short
iterations are going to continually increase the
stability, so aggregate stability at that point is around
0.5-0.6 as well.
0
500
1000
1500
2000
2500
3000
3500
4000
01020
Time and Effort
Completed
1 period
iteration
2 period
3 period
Figure 3: Efficiency over time with stable requirements.
The benefits of having multiple short iterations
for the situations with very unstable requirements
are clear from the simulation. We can also relate
these results to the practical iterative development
methods. One good example is the XP requirement
for an on-site customer who directly collaborates
with the development team (Beck, 1999), and we
have seen that daily customer contact had very good
results in numerous projects (Hwong, 2007). The
way to model this virtually constant customer review
is to assume short iterations with negligible fixed
iteration cost. According to our experience, and as
reported by other practitioners (Cohn, 2004), this
approach enables very rapid product development.
4 SIMULATION OF PREVIOUS
PROJECTS
We have been involved in several rapid development
projects using an iterative development process
(Hwong, 2007) and can use them as a basis for
validating the simulation results. We use data
collected from three projects, described in table 1.
The first two were done in parallel, had the same
schedule and staff levels, and only differed on the
initial stability of the requirement specifications. The
third project was done months later, based on the
same infrastructure and domain, and differed in
terms of staff while using the same basic schedule.
All three projects were based on three two-week
iterations. The same development process was used
for all three projects, and the simulation assumes the
same development speed, requirement impact, and
scope creep. The only two variables varying among
the three projects are the initial stability and size of
the initial requirement set. Three data points should
ENASE 2007 - International Conference on Evaluation on Novel Approaches to Software Engineering
116

give us a reasonable fit for the simulated processes
with only two free variables.
The simulation is based on the actual data
collected from the project effort tracking, and from
the developers’ opinion about the completion and
dropped effort ratio. The most influential and
variable parameter of the simulation is the
requirement stability. We assumed 0.8 initial
stability for one of the initial projects which started
after a significant agreement was reached on the
desired content, and we assumed that the other
project that started with a very fuzzy idea of the
desired outcome had the initial stability of 0.4. Since
the remaining project was developed subsequently
on the same infrastructure, it necessarily benefited
on the stability side. Thus, even though the initial
requirements were extremely fuzzy, we have
assumed its stability to be 0.6, the average of the
first two projects. Our goal for these simulations is
not to re-validate the previous results about short
iterations being very effective in requirement
maturation, but to use the simulation to determine
whether the iteration length on the projects was
optimally chosen.
Table 1: Project duration data.
P1 P2 P3
Number of
iterations
3 3 3
Iteration
duration
10 days 10 days 10 days
Team size 3 3 5
Table 2 shows the post-project estimates of the
work performed, work packages dropped after the
implementation, new work packages added to the
project during the development iterations, and
proposed work packages dropped during
requirement elaboration. The model was slightly
modified for these simulation to include scope creep.
We modelled scope creep in the form of adding
linearly more requirements than what was dropped
at the end of each iteration.
Table 2: Project completion data.
P1 P2 P3
Initial stability 0.8 0.4 0.6
Completed % 100% 80% 100%
Implemented,
Dropped %
5%-
10%
25% 10%
Added % 10% 15% 15%
Dropped % 5-10% 45% 25%
For the initial two projects, we found that 90 work
packages with uniform effort distribution matched
the project results in terms of completed work,
added effort, and work completed and then dropped.
For the third project, we found that the estimated
effort and completion was achieved with 110 - 130
work packages using the same distribution. These
complexity measures match the relative initial scope
of the projects. Subsequently, we used these values
as the initial requirement sets for simulating
different iteration lengths.
We performed a second simulation on the
established work package sets for the different
projects, and experimented with the number and
duration of the iterations, to evaluate the benefit of
shorter iterations. These simulations showed a small
improvement with shorter and more numerous
iterations, with the overall requirement stability
growing faster, and the overall delivery
completeness also closing in on the 100% mark.
Since the initial set of projects largely reached this
success level anyway, the primary difference is in
the cost of getting there.
The simulation shows that the completion of
delivery could be improved by 5% by having 4-5
iterations in the process. It also shows that a 2
iteration process would have achieved about the
same performance as the actual 3 iteration process
used in the projects. With 6 iterations, the cost of
fixed iteration overhead reduces the performance.
These simulations suggest that there is an optimal
range of iteration durations, which is a topic for
further study.
5 USE OF REQUIREMENT
STABILITY IN ITERATION
PLANNING
Our results confirm the intuitive value of frequently
reviewing the developers’ work with the customers
in order to improve the understanding and maturity
of the product requirements (Song, 2005). Agile
development processes commonly require high level
of customer involvement, in some cases going as far
as full time collocating them with the team. The
collocated customer is able to do almost constant
informal reviews, with a very low productivity cost
to the team. However, domain experts who can
provide a proper depth of review for both the
business and technical implementation issues are
rarely available for full time participation, since their
expertise is often required in the maintenance and
USE OF REQUIREMENT STABILITY IN OPTIMIZING ITERATIVE DEVELOPMENT PROCESSES
117

management of multiple existing products. Iterative
development processes must be able to
accommodate domain experts who are not available
full time.
Our suggested approach to determining the
iteration length is to make them as short as practical,
within the constraints of reviewer availability in
order to ensure timely reviews of implemented
features.
The primary aspect of feedback that leads to the
increase in requirement stability in our simulations is
based on the communication between the developers
and customers, and sharing of knowledge. When this
feedback only happens at the end of iteration the
simulation indicates that shorter iterations are
preferable to longer ones in the initial stages of the
project. On the other hand, in terms of pure project
management and scheduling, having the team
iterations constant brings a significant amount of
value in terms of establishing a development
rhythm. The increased communication needed for
improving the stability of the requirements can also
be satisfied by conducting multiple reviews during a
standard iteration. These reviews should not require
fully tested and documented system components.
When the requirements are immature, timely
feedback is more relevant than completeness..
Requirement stability can be estimated from data
that is directly measurable as part of management of
iterative development processes. At the end of an
iteration review, we know the amount of effort that
went into the development during the iteration, and
we will be able to estimate the ratio of effort that
resulted in rejected packages. The ratio of effort in
accepted packages to the total of reviewed packages
can be used as a measure of requirement stability.
Overall stability below the 0.5 threshold suggests the
use of short iterations or frequent customer reviews.
As the requirement stability grows, the frequency of
review sessions can be reduced accordingly.
In practice, it is rare that all the requirements of a
system are at a very low level of stability, as most
systems will have some mature and well defined
requirements. The system at large would be well
served by longer, synchronized iterations with
multiple agile teams since most of the requirements
are relatively stable. However, the volatile aspects of
the application require a more dynamic approach,
where multiple review sessions per iteration would
improve the understanding and stability of the
requirements. Teams working on these features can
remain synchronized with other teams while using
frequent reviews to address requirement volatility.
6 CONCLUSION
We have shown that requirement stability is an
important element that should be taken into account
when planning and executing software development
projects. We have also identified some types of
software development projects which get started
with a very low requirement stability level, and in
their very early phases need to rely heavily on
frequent progress reviews. Our results confirm the
intuitive hypothesis that postponing the reviews until
the completion of longer iterations leads to larger
amounts of wasted effort, and slower maturation of
the product requirements. Finally we have provided
an evaluation approach that allows project managers
to estimate their requirement stability, and to plan
for a more effective development process by
adjusting the interval between customer reviews.
REFERENCES
Beck, K., 1999. Extreme Programming Explained:
Embrace Change, Addison-Wesley.
Cohn, M., 2004. User Stories Applied : For Agile
Software Development. Addison-Wesley Professional.
Demarco, T., Lister, T., 2003. Waltzing With Bears:
Managing Risk on Software Projects, Dorset House
Publishing Company.
Fayad, M., Altman, A, 2001. An Introduction to Software
Stability. In COMMUNICATIONS OF THE ACM
September 2001/Vol. 44, No. 9
Hwong, B., Matos, G., McKenna, M., Nelson, C.,
Nikolova, G., et al, 2007. “Quality Improvements
From Using Agile Development Methods: Lessons
Learned”, In I. Stamelos, P. Sfetsos (eds.), Agile
Software Development Quality Assurance, IGI Global
Javed, T., Maqsood, M., Durrani, Q., 2004. A Study to
Investigate the Impact of Requirements Instability on
Software Defects, in ACM Software Engineering
Notes, Volume 29, Number 4 , May 2004.
Jones, C., 1998. Estimating Software Costs, McGraw-Hill.
Pfahl, D., Lebsanft, K., 2000. Using Simulation to
Analyze the Impact of Software Requirement
Volatility on Project Performance, in Information and
Software Technology 42, 2000.
Schwaber, K., Beedle , M., 2001. Agile Software
Development with SCRUM, Prentice Hall.
Song, X., Matos, G., Hwong, B., Rudorfer, A., Nelson, C.,
2005. S-RaP: A Concurrent Prototyping Process for
Refining Workflow-Oriented Requirements, in RE’05
International Conference on Requirement Engineering
, Sept, 2005. Paris, France.
ENASE 2007 - International Conference on Evaluation on Novel Approaches to Software Engineering
118
