AUTOMATIC BREAST CONTOUR DETECTION IN DIGITAL

PHOTOGRAPHS

Jaime S. Cardoso, Luis F. Teixeira

INESC Porto, Faculdade de Engenharia, Universidade do Porto, Portugal

Maria J. Cardoso

Faculdade de Medicina, Universidade do Porto, Portugal

Keywords:

Computer-aided medical system, breast cancer conservative treatment, breast contour, shortest path problem.

Abstract:

Breast cancer conservative treatment (BCCT), due to its proven oncological safety, is considered, when fea-

sible, the gold standard of breast cancer treatment. However, aesthetic results are heterogeneous and difﬁcult

to evaluate in a standardized way, due to the lack of reproducibility of the subjective methods usually ap-

plied. The objective assessment methods, considered in the past as being less capable of evaluating all aspects

of BCCT, are nowadays being preferred to overcome the drawbacks of the subjective evaluation. A recent

computer-aided medical system was developed to objectively and automatically evaluate the aesthetic result

of BCCT. In this system, the detection of the breast contour on the digital photograph of the patient is a nec-

essary step to extract the features subsequently used in the evaluation process. In this paper an algorithm

based on the shortest path on a graph is proposed to detect automatically the breast contour. The proposed

method extends an existing semi-automatic algorithm for the same purpose. A comprehensive comparison

with manually-drawn contours reveals the strength of the proposed method.

1 INTRODUCTION

Breast cancer conservative treatment (BCCT) has

been increasingly used over the last twenty years due

to identical survival resultswhen comparedto mastec-

tomy, and a better cosmetic outcome. Although con-

siderable research has been put into the oncological

aspects of BCCT, diverse aesthetic results are com-

mon due to the difﬁcult standardization of this type

of treatment, stressing the importance of the aesthetic

evaluation in institutions dedicated to breast cancer

treatment so as to improve working practices.

The ﬁrst and more generalized methods used for

aesthetic evaluation of BCCT were the subjective ap-

preciation of the patient, directly or through pho-

tographs, by one ore more observers (Harris et al.,

1979). The categorization of the aesthetic result,

subjectively estimated and combined by observers

through this visual inspection relies on the complex

interplay of multiple factors. Considering the subjec-

tivity of any human decision, the obtained results are

questionable and frequently the reproducibility values

obtained among observers are only modest. In fact,

this lack of reproducibility has been shown by oth-

ers (Christie et al., 1996), which creates uncertainty

when comparing results between studies. It has also

been demonstrated that observers from different pro-

fessional backgrounds evaluate cases differently, at-

taining even lower agreement results (Cardoso et al.,

2005).

Objective methods of evaluation have emerged as

a way to overcome these drawbacks of the subjective

evaluation. Initially they consisted only in the com-

parison between the two breasts of simple measure-

ments marked directly in patients or in photographs

(Limbergen et al., 1989; Christie et al., 1996). The

correlation of objectivemeasurements with subjective

overall evaluation has been reported by several au-

thors (Christie et al., 1996). Trying to overcome the

sense that objective asymmetry measurements were

insufﬁcient, other groups proposed the sum of the in-

dividual scores of subjective and objective individual

indices (Al-Ghazal et al., 1999). More recently, a

computer-aided medical system was developed to ob-

jectively and automatically perform the aesthetic eval-

uation of BCCT (Cardoso and Cardoso, 2007b). The

S. Cardoso J., F. Teixeira L. and J. Cardoso M. (2008).

AUTOMATIC BREAST CONTOUR DETECTION IN DIGITAL PHOTOGRAPHS.

In Proceedings of the First International Conference on Health Informatics, pages 91-98

 SciTePress

development of this system entailed the automatic ex-

traction of severalfeatures from the photographs(Fig-

ure 1), capturing some of the factors considered to

have impact on the overall cosmetic result: breast

asymmetry, skin colour changes due to the radiother-

apy treatment and surgical scar visibility. In a sec-

ond phase, a support vector machine classiﬁer was

trained to predict the overall cosmetic result from the

recorded features (Cardoso and Cardoso, 2007b).

(a) (b) (c)

Figure 1: Typical photographs.

In order to extract the identiﬁed relevant features

from the image, the detection of the breast contour

is necessary. In (Cardoso and Cardoso, 2007a) the

authors describe a semi-automatic method for the de-

tection of the breast contour. The user has to manu-

ally identify the two endpoints of the breast contour.

Subsequently, the algorithm automatically ﬁnds the

contour in-between. The algorithm has been imple-

mented in a computer-aided medical system: the soft-

ware automatically ﬁnds the contours, extracts rele-

vant features and outputs a predicted overall cosmetic

assessment (excellent, good, fair, or poor).

Here, we improve on the work of (Cardoso and

Cardoso, 2007a) in two different directions. First, we

present an algorithm for the automatic detection of the

endpoints of the breast contour, thus eliminating any

user input from the process. Therefore a totally auto-

matic breast contour detection is achieved. Next, we

provide a thorough evaluation of the performance of

the proposed method against manually-drawn breast

contours. Standard metrics are employed to compare

two contours.

Before presenting the proposed approach, and for

completeness, we recover the framework for breast

contour detection between two known endpoints of

(Cardoso and Cardoso, 2007a). Then, in section 3

we detail how to automatically ﬁnd the endpoints of a

breast contour. Examples are provided and a perfor-

mance analysis is conducted in section 4. Finally, in

section 5, we conclude the paper and present possible

directions of future work.

2 A SHORTEST PATH APPROACH

TO CONTOUR DETECTION

When knowing the two endpoints of the breast con-

tour, we are left with the problem of ﬁnding the path

between both endpoints that goes through the breast

contour. As the interior of the breast itself is essen-

tially free of edges, the path we are looking for is the

shortest path between the two endpoints, if paths (al-

most) entirely through edge pixels are favoured. More

formally, let s and t be two pixels of the image and P

s,t

a path over the image connecting them. We are inter-

ested in ﬁnding the path P that optimizes some pre-

deﬁned distance d(s,t). This criterion should embed

the need to favour edge pixels.

In the work to be detailed, the image grid is con-

sidered as a graph with pixels as nodes and edges con-

necting neighbouring pixels. Therefore, some graph

concepts are in order.

2.1 Deﬁnitions and Notation

A graph G = (V,A) is composed of two sets V and

A. V is the set of nodes, and A the set of arcs (p,q),

p,q ∈ V. The graph is weighted if a weight w(p,q)

is associated to each arc, and it is called a digraph

if the arcs are directed, i.e., (p,q) 6= (q, p). A path

from p

to p

is a list of unique nodes p

, p

,. .. , p

, p

i+1

) ∈ A. The path cost is the sum of each arc

weight in the path.

In graph theory, the shortest-path problem seeks

the shortest path connecting two nodes; efﬁcient al-

gorithms are available to solve this problem, such as

the well-known Dijkstra algorithm (Dijkstra, 1959).

2.2 Proposed Algorithm

If the weight assigned to an edge captures the in-

tensity of the contour of the adjacent pixels, ﬁnding

the best contour translates into computing the min-

imum accumulated weight along all possible curves

connecting s and t:

d(s,t) = min

s,t

∑

w(p, q). (1)

Note that, if we ignore the weight component, we are

simply computing the regular Euclidian distance be-

tween s and t along the path P

s,t

(which will be a

straight line for the shortest path).

Therefore, to detect the breast contour in (Car-

doso and Cardoso, 2007a) it is proposed a two step

approach:

1. Apply an edge detector to the original image

(other operations, replacing the edge detector, will

be proposed latter in this work). The resulting bi-

nary image enhances the points of interest.

2. Detect the breast contour on the edge image, by

ﬁnding the shortest path between the two end-

points.

We now detail this second step.

Starting by modelling the edge image as a graph,

correspond a node to each pixel. Connect two nodes

with an arc on the graph iff the corresponding pixels

are neighbours (8-connected neighbourhoods) on the

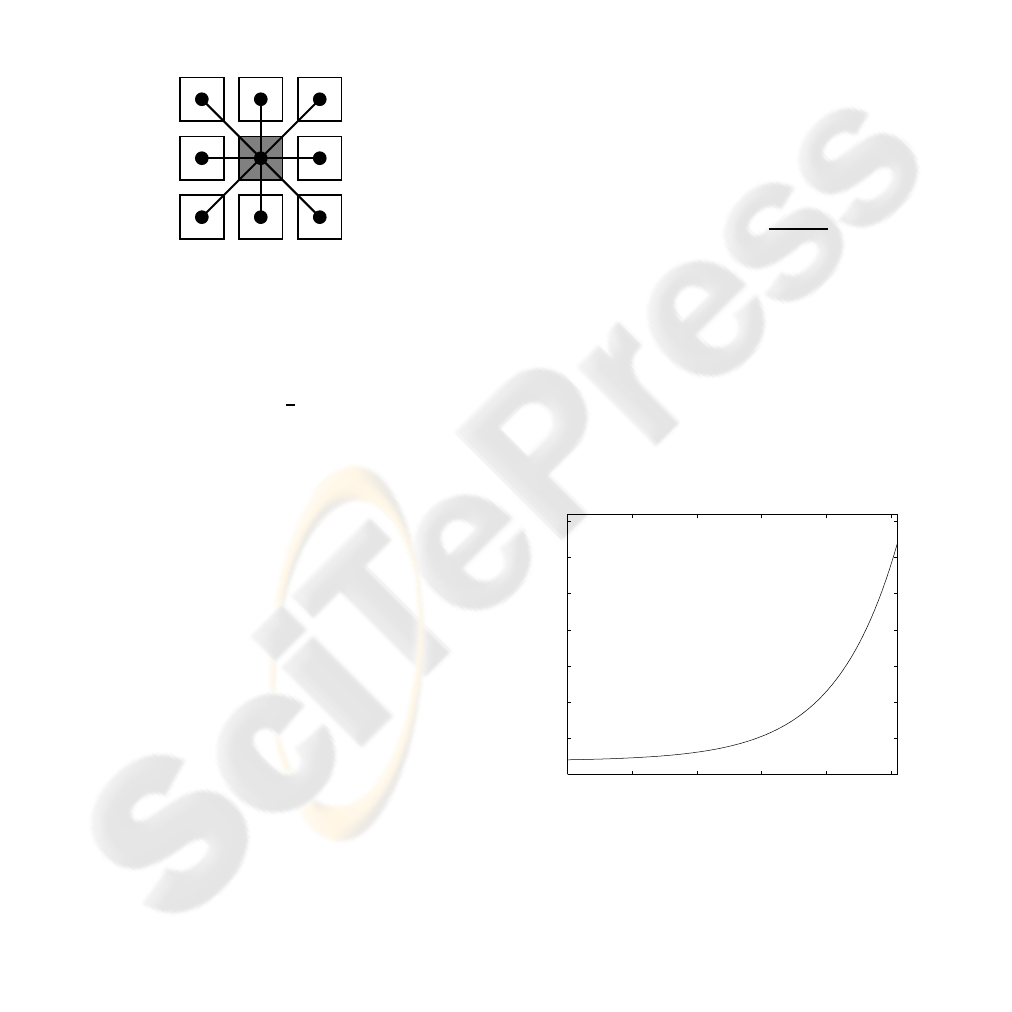
image. The weight of each arc is a function of pixels

values and pixels relative positions — see Figure 2:

Figure 2: Arc weight between two pixels.

(

f(p,q

) if q

∈ 4-connected neighbourhood of p

h(p,q

) if q

6∈ 4-connected neighbourhood of p

In this work we set h(.,.) =

(2) f(., .).

Now, to favour paths through edge pixels, one can

set

f(p,q) =

(

if both p and q are edge pixels

otherwise

with c

> c

. In this work c

and c

were experi-

mentally determined as 2 and 32, respectively. Note

that c

must be set greater than zero, to also favour

the smallest path, when more than one exists through

edge pixels only. Finally, the solution to the shortest

path problem will yield the intended breast contour.

2.3 Algorithm Generalization

The proposed paradigm can be conveniently general-

ized. The application of an edge detector in the ﬁrst

step can miss to detect segments of the breast con-

tour. This is especially true for women with small

breasts (leading to weak contours) or when the breast

is severely deformed with the excision of a large sam-

ple of tissue. A natural improvement is to replace

the binary image outputted by the edge detector with

a richer gradient image. Now, the shortest path al-

gorithm should try to follow pixels with high gra-

dient values. Thus, the f(.,.) and h(., .) functions

have to be properly generalized. A simple strategy

is to set f(p,q) =



255 − min(grad(p),grad(q))



where

f(.) is a monotonically increasing function.

Note that this more general setting has the binary case

as a particular instantiation. To summarize, the pro-

posed general framework to ﬁnd the contour between

two endpoints encompasses:

• A gradient computation of the original image. In a

broader view, this can be replaced by any feature

extraction process that emphasizes the pixels we

are seeking for.

• Consider the gradient image as a weighted graph

with pixels as nodes and edges connecting neigh-

bouring pixels. Assign to an edge the weight

= f(p, q) or w

= h(p,q), as described before.

The gradient model adopted in the experiments re-

ported latter is based on the Sobel operator. The So-

bel operator is applied on the x and y directions; from

the computed values, S

and S

, the magnitude of the

gradient is estimated as z =

+ S

. Costs were

assigned based on an exponential law:

f(z) = αexp(βz) + δ, α,β, δ ∈ ℜ

The parameters α,β, δ were chosen to yield

f(0) = 2

and

f(255) = 32, leading to the same range of costs

as the binary model. The third degree of freedom was

experimentally tuned. The adopted transformation

was (see also Figure 3)

f(z) = 0.15exp(0.0208z) +

1.85.

0 50 100 150 200 250

input

Figure 3: Transformation

f(.).

3 AUTOMATIC DETECTION OF

ENDPOINTS

The challenge now is to automatically extract the end-

points. In order to address this key problem we will

assume, very reasonably, that the photo contains only

the torso of the patient.

The position of the external endpoint of the breast

contour can be assumed at the point of the body where

the arm contour intersects the trunk contour. How-

ever, because patients are in the arms-down position,

the arm’s contour is almost indistinguishable from the

trunk’s contour. Therefore, we deﬁne the external

endpoint of the breast contour as the highest point of

the trunk contour.

The approach just delineated requires ﬁrst the de-

tection of the trunk contour. That may be searched

among the strongest lines of gradient with approxi-

mate vertical direction.

In order to get a ﬁrst intuition of the general result,

it is instructive to explore a basic example. Consider

in Figure 4(a) the gradient intensity, with black pixels

representing high intensity values.

(a) A single vertical line

of nonzero gradient.

(b) The shortest path be-

tween some points on the

bottom and the top mar-

gin.

Figure 4: A ﬁrst exempliﬁcative example.

In Figure 4(b) the shortest paths between starting

points s

on the bottom row and the whole top row

are traced. The distance between a ﬁxed point on the

bottom row and the whole top row can be generally

formulated as the distance between a point s and a

region Ω. The distance from a pixel s and a region Ω

is given by

d(s,Ω) = min

t∈Ω

d(s,t), (2)

where d(s,t) was deﬁned previously. All the traced

paths got attracted by the vertical line.

Phase 1: we propose to apply this procedure to the

bottom half of our photographs:

1. Compute the gradient of the image (see Fig-

ure 5(a)).

2. Compute the shortest path between each point in

the bottom row and the whole middle row of the

gradient image (see Figure 5(b)).

3. Compute the shortest path between each point in

the middle row and the whole bottom row of the

gradient image (see Figure 5(c)).

4. Discard all paths except for those common to

steps 2 and 3 (see Figure 5(d)).

5. Discard paths with a cost superior to half of the

maximum possible cost (see Figure 5(e)). Finally,

the trunk contour is deﬁned as the two contours

closest to the middle of the photograph.

(a) Gradient. (b) Shortest paths from

a pixel s in the bot-

tom line and the whole

middle row Ω

, super-

imposed on the original

image.

a pixel s in the mid-

dle row and the whole

bottom row Ω

, super-

imposed on the original

image.

(d) Strong paths be-

tween the middle and

bottom rows.

(e) Selected paths, su-

perimposed on the orig-

inal image.

(f) Strong paths be-

tween the top and

bottom rows.

(g) The external end-

point of the breast con-

tour is the highest point

of the shortest path.

(h) Totally automated

breast contour.

Figure 5: Results for a real photograph.

It is appropriate to introduce now the concept of

strong path.

Deﬁnition. A path P

s,t

is a strong path between re-

gions Ω

and Ω

if P

s,t

is the shortest path between

s ∈ Ω

and the whole region Ω

, and P

s,t

is the short-

est path between t ∈ Ω

and the whole region Ω

With this deﬁnition, steps 2, 3 and 4 are just the

computation of the strong paths between the middle

and bottom rows.

At the end of this phase we have already the po-

sition of the two trunk contours, but we have stopped

the process at the middle of the image. Perhaps it is

important to stress that if the process was conducted

between the bottom and top rows, the trunk contours

would be lost, as the only strong paths between the

top and bottom rows would be the external silhouette

of the patient (see Figure 5(f)) .

Phase 2: to determine the top of the trunk contour,

we need to continue the path produced in phase 1 un-

til a certain condition is met. Towards that end, we

propose to ﬁnd the shortest path between the end-

ing point of the strong contour found in phase 1 and

row R

= middle row,· ·· ,top row. We select the

highest row for which the shortest path does not con-

tain a long sequence (

LENGTHTHRESHOLD

) of consec-

utive pixels with low gradient (

GRADIENTTHRESHOLD

Figure 5(g) illustrates the results obtained for the

exempliﬁcative photograph (

LENGTHTHRESHOLD

and

GRADIENTTHRESHOLD

were set to 12 and 48, respec-

tively).

Before applying the algorithm presented in Sec-

tion 2 to compute the breast contour we need also

the internal endpoint of the breast contour. This was

estimated simply as the middle point between the

two external endpoints. Finally, the computation of

the breast contour yields the result presented in Fig-

ure 5(h).

4 RESULTS

The methodology proposed in this paper was assessed

on a set of photographs from 120 patients. The pho-

tographs were collected in three different institutions

in Portugal. All patients were treated with conserva-

tive breast surgery, with or without auxiliary surgery,

and whole breast radiotherapy, with treatment com-

pleted at least one year before the onset of the study.

Breast images were acquired employing a 4M pixel

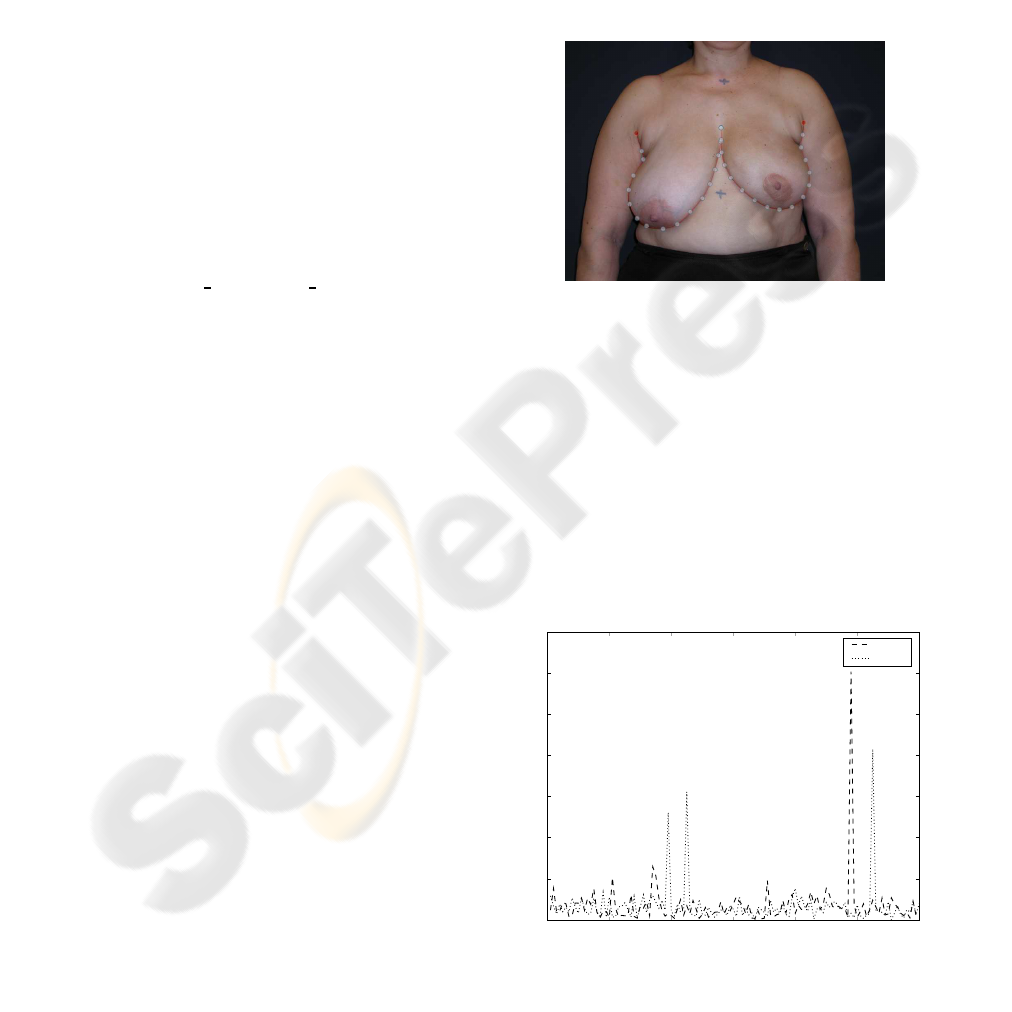
digital camera. A mark was made on the skin at the

suprasternal notch and at the midline 25 cm below the

ﬁrst mark (see Figure 1). These two marks create a

correspondence between pixels measured on the dig-

ital photograph and the length in centimetres on the

patient.

In order to investigate the possibility of deﬁning

an automated method of detecting the breast contour,

a set of patients with known breast contour was re-

quired. Since, ideally, the automated method should

correlate coherently with human assessment, eight

different observers were asked to manually draw the

contours. A software tool was developed speciﬁcally

to assist on this job. The user deﬁnes the contour by

positioning seventeen control points of cubic splines,

see Figure 6.

Figure 6: Software for manual breast contour deﬁnition.

Before applying the proposed algorithm, each im-

age was downsized to a constant width of 768 pix-

els, while keeping the aspect ratio. This improves the

computational performance of the implementation of

the software, without degrading the quality of the ﬁ-

nal result.

Figure 7 shows the evolution of the error when es-

timating the external endpoints’ position of the breast

contour. The error in pixels was scaled to centimetres

with the help of the marks made on the skin of the

patient. Table 1 summarizes the results.

0 20

60 80

100 120

patient number

distance (cm)

left

right

Figure 7: Evolution of error (cm) in the position of the ex-

ternal endpoints of the breast contour over 120 photographs.

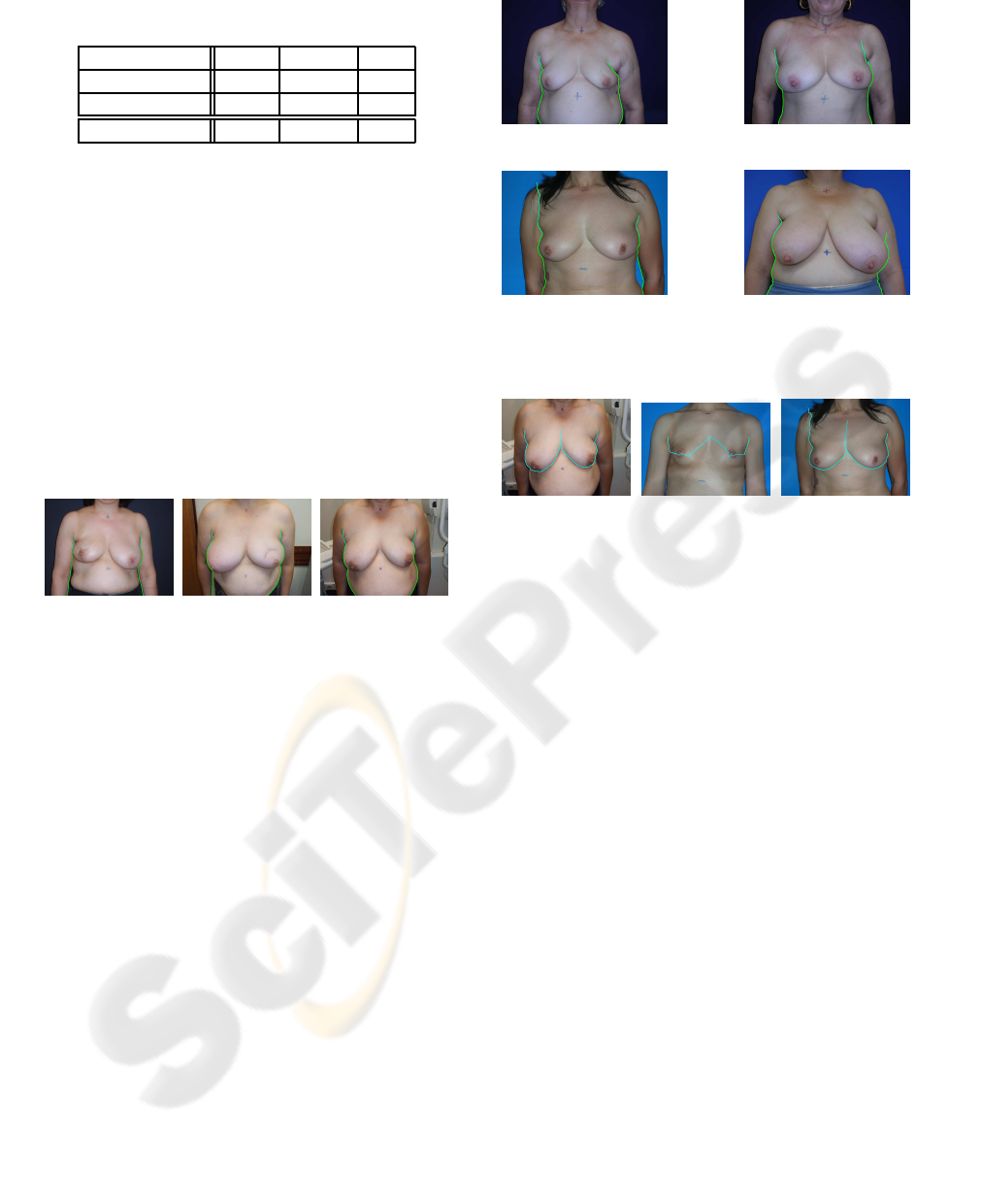
Table 1: Mean, standard deviation and maximum value of

errors in the position of the endpoints.

Error (cm) mean std dev max

left endpoint 0.7 1.1 12.1

right endpoint 0.7 1.0 8.3

total 0.7 1.1 12.1

It can be observed that the proposed algorithm

has a very interesting performance. The average er-

ror is quite low, less than 1 centimetre. Figure 8

shows some of the photographs for each the algorithm

worked satisfactorily. It represents the result after the

two phases of the algorithm. The highest point of the

trunk contour provides the detected external endpoint

of the breast contour. It is visible in patient #35 that

the algorithm is robust against cluttered background.

It is also visible in Figure 8 that, although the strong

paths detected in phase 1 do not always correspond

exactly to the trunk contour, the algorithm is still able

to successfully detect the endpoints.

(a) Patient #05. (b) Patient #22. (c) Patient #35.

Figure 8: Selected successful results.

Nevertheless, four endpoints were clearly mis-

placed. These results, displayed in Figure 9, bring to

light some of the limitations of the current state of the

proposed approach. In patients #39, #45 and #105 the

shortest path followed a ‘wrong’ contour, misplacing

the endpoint. With patient #98 the long hair created a

false ‘path’ till the top of the image.

After the automatic detection of the endpoints, the

algorithm detailed in Section 2 to ﬁnd the breast con-

tour was applied to the photographs. Different scenar-

ios can take place:

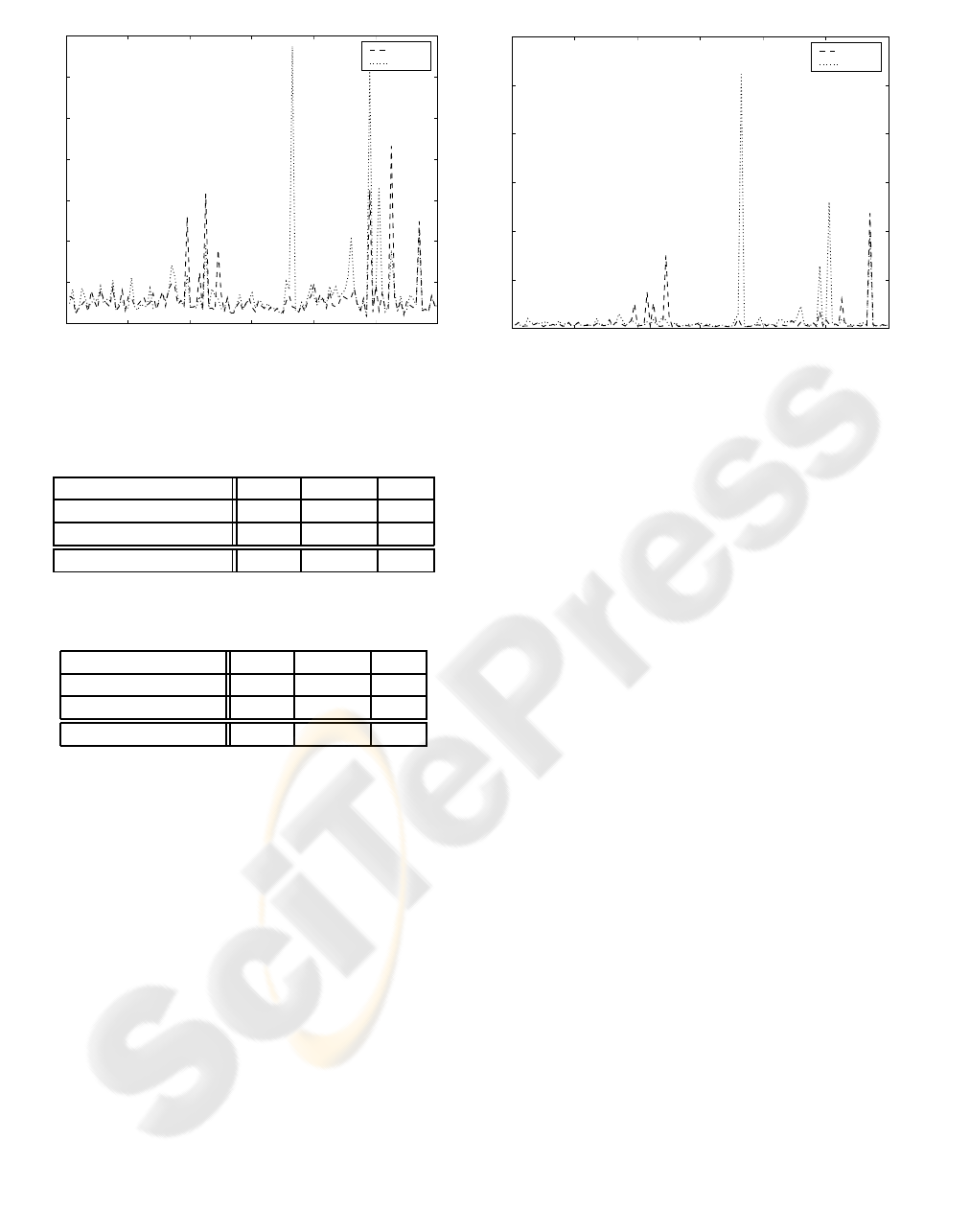
1. The endpoints were successfully located and the

breast contour is correctly found. This desirable

result is illustrated in Figure 10(a).

2. The endpoints were successfully located but the

algorithm misses to follow adequately the breast

contour (see Figure 10(b)).

3. The endpoints were poorly located but the algo-

rithm rapidly ﬁnds and tracks the right breast con-

tour (see Figure 10(c)).

4. The endpoints were poorly located and the breast

contour is incorrectly tracked (this scenario did

not occur in the experimental set of photographs).

(a) Patient #39. (b) Patient #45.

Figure 9: All poor results.

(a) Patient #35. (b) Patient #114. (c) Patient #98.

Figure 10: Breast contour results.

In a last set of experiments, the quality of the

breast contour tracking algorithm was assessed. In-

stead of a simple subjective evaluation as provided in

(Cardoso and Cardoso, 2007a), we conducted a com-

plete objective evaluation, based on the hausdorff and

the average distances to compare two contours. The

hausdorff distance is deﬁned as the “maximum dis-

tance of a set to the nearest point in the other set”.

Roughly speaking, it captures the maximum separa-

tion between the manual and the automatic contours.

As observed in Figure 11 and Table 2 the experimen-

tal values obtained for the hausdorff distance corre-

late well with the error on the endpoints. This fact

means that, most of the times, the major error on the

automatic contour is located on the endpoint, with the

shortest path algorithm recovering the true contour

rapidly. A clear exception is patient #73, for which

the error in the endpoints is negligible but the haus-

dorff distance between contours is very high. Here,

the contour tracking algorithm missed to follow the

contour, although it received proper endpoints.

The average distance between two contours cap-

tures better the perceived quality of the automatic

breast contour. Here, the distance is averaged over

the whole contour. Figure 12 and Table 3 summarize

these results. As expected by visual inspection pa-

tient of #98 in Figure 10(c), although the error on the

endpoint’s location was high, the breast contour algo-

0 20

60 80

100 120

patient number

hausdorff distance (cm)

right

left

Figure 11: Evolution of hausdorff distance (cm) in the po-

sition of the breast contour over 120 photographs.

Table 2: Mean, standard deviation and maximum value of

hausdorff distance in the position of the breast contour.

Hausdorff dist. (cm) mean std dev max

left endpoint 1.5 1.7 13.5

right endpoint 1.3 1.2 8.7

total 1.4 1.5 13.5

Table 3: Mean, standard deviation and maximum value of

average distance in the position of the breast contour.

Average dist. (cm) mean std dev max

left endpoint 0.2 0.6 5.2

right endpoint 0.1 0.3 2.4

total 0.2 0.4 5.2

rithm recovered rapidly, translated into a small aver-

age distance (but a high hausdorff distance).

The consequences of the diverse errors enumer-

ated before to the computer-aided medical system are

different and have to be further studied. For exam-

ple, one of the features used for the objectiveaesthetic

evaluation of the BCCT is the difference between the

levels of inferior breast contour points. This measure

is quite robust over strong errors on the endpoints’

position, as long as the breast contour is correctly

tracked. Other features, such as the difference in the

area of the breast are much more sensible to the posi-

tioning of the endpoints. One line of future investiga-

tion is the selection of features robust to the common

errors of the automatic detection of notable points

(contour endpoints, breast contour, nipples, etc) but

still capturing adequately the aesthetic result, leading

to a good classiﬁcation performance.

0 20

60 80

100 120

patient number

average distance (cm)

right

left

Figure 12: Evolution of the average distance (cm) in the

position of the breast contour over 120 photographs.

5 CONCLUSIONS

A method has been described for applying graph con-

cepts to the task of automatically extracting the breast

contour in digital photographs of the torso of a pa-

tient, after submitted to a breast cancer conservative

treatment. In the proposed framework the problem of

ﬁnding the endpoints of the breast contour is formu-

lated as a problem of ﬁnding strong contours between

two regions, a concept introduced here for the ﬁrst

time. The breast contour is found as the solution to

the shortest problem on a graph, after conveniently

modelling the image as a weighted graph. Prelimi-

nary results indicate an excellent performance in the

task of ﬁnding the external endpoints of the contour

and a good performance on detecting the breast con-

tour. Future work will focus on improvements to the

algorithm including generalizing the solution to other

typical patient positions in these studies.

ACKNOWLEDGEMENTS

This work was partially funded by Fundac¸˜ao para

a Ciˆencia e a Tecnologia (FCT) - Portugal through

project PTDC/EIA/64914/2006.

REFERENCES

Al-Ghazal, S. K., Blamey, R. W., Stewart, J., and Morgan,

A. L. (1999). The cosmetic outcome in early breast

cancer treated with breast conservation. European

journal of surgical oncology, 25:566–570.

Cardoso, J. S. and Cardoso, M. J. (2007a). Breast contour

detection for the aesthetic evaluation of breast cancer

conservative treatment. In International Conference

on Computer Recognition Systems (CORES’07).

Cardoso, J. S. and Cardoso, M. J. (2007b). Towards an in-

telligent medical system for the aesthetic evaluation of

breast cancer conservative treatment. Artiﬁcial Intel-

ligence in Medicine, 40:115–126.

Cardoso, M. J., Santos, A. C., Cardoso, J. S., Barros, H.,

and Oliveira, M. C. (2005). Choosing observers for

evaluation of aesthetic results in breast cancer conser-

vative treatment. International Journal of Radiation

Oncology, Biology and Physics, 61:879–881.

Christie, D. R. H., O’Brien, M.-Y., Christie, J. A., Kron,

T., Ferguson, S. A., Hamilton, C. S., and Denham,

J. W. (1996). A comparison of methods of cosmetic

assessment in breast conservation treatment. Breast,

5:358–367.

Dijkstra, E. W. (1959). A note on two problems in connex-

ion with graphs. Numerische Mathematik, 1:269–271.

Harris, J. R., Levene, M. B., Svensson, G., and Hellman,

S. (1979). Analysis of cosmetic results following pri-

mary radiation therapy for stages i and ii carcinoma of

the breast. International Journal of Radiation Oncol-

ogy Biology Physics, 5:257–261.

Limbergen, E. V., Schueren, E. V., and Tongelen, K. . V.

(1989). Cosmetic evaluation of breast conserving

treatment for mammary cancer. 1. proposal of a quan-

titative scoring system. Radiotherapy and oncology,

16:159–167.