HUMAN

FACE VERIFICATION BASED ON MULTIDIMENSIONAL

POLYNOMIAL POWERS OF SIGMOID (PPS)

ao Fernando Marar

Department of Computing, Adaptive Systems and Computational Intelligence Laboratory

Faculdade de Ci

encias, S

ao Paulo State University, Bauru , S

ao Paulo, Brazil

Helder Coelho

Department of Informatics, Laboratory of Agent Modelling

Faculdade de Ci

encias, Lisbon University, Lisbon, Portugal

Keywords:

Artiﬁcial Neural Network, Human Face Veriﬁcation, Polynomial Powers of Sigmoid (PPS), Wavelets Func-

tions, PPS-Wavelet Neural Networks, Activation Functions, Feedforward Networks.

Abstract:

In this paper, we described how a multidimensional wavelet neural networks based on Polynomial Powers of

Sigmoid (PPS) can be constructed, trained and applied in image processing tasks. In this sense, a novel

and uniform framework for face veriﬁcation is presented. The framework is based on a family of PPS

wavelets,generated from linear combination of the sigmoid functions, and can be considered appearance based

in that features are extracted from the face image. The feature vectors are then subjected to subspace projection

of PPS-wavelet. The design of PPS-wavelet neural networks is also discussed, which is seldom reported in the

literature. The Stirling Universitys face database were used to generate the results. Our method has achieved

92 % of correct detection and 5 % of false detection rate on the database.

1 INTRODUCTION

Systems based on biometric characteristics, such as

face, ﬁngerprints, geometry of the hands, iris pat-

tern and others have been studied with attention.

Face veriﬁcation is a very important of these tech-

niques because through it non-intrusive systems can

be created, which means that people can be compu-

tationally identiﬁed without their knowledge. This

way, computers can be an effective tool to search for

missing children, suspects or people wanted by the

law. Mathematically speaking, human face veriﬁca-

tion problem can be formulated as function approxi-

mation problems and from the viewpoint of artiﬁcial

neural networks these can be seen as the problem of

searching for a mapping that establishes a relationship

from an input to an output space through a process of

network learning.

Wavelet functions have been successfully used in

many problems as the activation function of feedfor-

ward neural networks. An abundance of R&D has

been produced on wavelet neural network area. Some

successful algorithms and applications in wavelet

neural network have been developed and reported in

the literature (Pati and Krishnaprasad, 1993; Marar,

1997; Oussar and Dreyfus, 2000; Fan and Wang,

2005; Zhang and Pu, 2006; Avci, 2007; Jiang et al.,

2007; Misra et al., 2007).

However, most of the aforementioned reports im-

pose many restrictions in the classical backpropaga-

tion algorithm, such as low dimensionality, tensor

product of wavelets, parameters initialization, and, in

general, the output is one dimensional, etc.

In order to remove some of these restrictions,

we develop a robust three layer PPS-wavelet multi-

dimensional strongly similar to classical multilayer

perceptron. The great advantage of this new approach

is that PPS-Wavelets offers the possibility choice of

the function that will be used in the hidden layer,

without need to develop a new learning algorithm.

This is a very interesting property for the design of

new wavelet neural networks architectures. This pa-

per is organized as follows. Section 2 introduces the

wavelet sigmoidal function. Section 3 presents the

framework used in this research. Section 4 deals with

application of human face veriﬁcation problem. Sec-

tion 5 concludes this paper.

Fernando Marar J. and Coelho H. (2008).

HUMAN FACE VERIFICATION BASED ON MULTIDIMENSIONAL POLYNOMIAL POWERS OF SIGMOID (PPS).

In Proceedings of the First International Conference on Health Informatics, pages 99-106

 SciTePress

2 WAVELET FUNCTIONS

Two categories of wavelet functions, namely, or-

thogonal wavelets and wavelet frames (or non-

orthogonal), were developed separately by different

interests. An orthogonal basis is a family of wavelets

that are linearly independent and mutually orthogo-

nal, this eliminates the redundancy in the representa-

tion. However, orthogonal wavelets bases are difﬁcult

to construct because the wavelet family must satis-

fy stringent criteria (Daubechies, 1992). This way,

for these difﬁculties, orthogonal wavelets is a serious

drawback for their application to function approxi-

mation and process modeling (Oussar and Dreyfus,

2000). Conversely, wavelet frames are constructed by

simple operations of translation and dilation of a sin-

gle ﬁxed function called the mother wavelet, which

must satisfy conditions that are less stringent than or-

thogonality conditions.

Let ϕ

(x) a wavelet, the relation:

(x) = ϕ(d

.(x−t

))

where t

is the translation factors and d

is the dilation

factors ∈ R. The family of functions generated by f

can be deﬁned as:

f =

ϕ(d

.(x−t

)),t

and d

∈ R

A family f is said to be a frame of L

(R) if there

exist two constants c > 0 and C < ∞ such that for any

square integrable function f the following inequali-

ties hold:

ckf k

≤

∑

| < ϕ

, f > |

≤Ckf k

where ϕ

∈ f, kf k denotes the norm of function f

and < ϕ

, f > the inner product of functions. Fa-

milies of wavelet frames of L

(R) are universal ap-

proximators (Pati and Krishnaprasad, 1993; Marar,

1997). In this work, we will show that wavelet frames

allow practical implementation of multidimensional

wavelets. This is important when considering prob-

lems of large input and output dimension. For the

modeling of multi-variable processes, such as, the ar-

tiﬁcial neural networks biologically plausible, multi-

dimensional wavelets must be deﬁned. In the present

work, we use multidimensional wavelets constructed

as linear combination of sigmoid, denominated Poly-

nomial Powers of Sigmoid Wavelet (PPS-wavelet).

2.1 Sigmoidal Wavelet Functions

In (Funahashi, 1989) is showed that:

Let s(x) a function different of the constant func-

tion, limited and monotonically increase. For any

0 < α < ∞ the function created by the combination

of sigmoid is described in Equation 1:

g(x) = s(x+ α) −s(x −α) (1)

where g(x) ∈ L

(R), i.e,

∞

−∞

g(x) < ∞

in particular, the sigmoid function satisﬁes this pro-

perty.

Using the property came from the Equation 1, in

(Pati and Krishnaprasad, 1993) boundary suggest the

construction of wavelets based on addition and sub-

traction of translated sigmoidal, which denominates

wavelets of sigmoid. In the same article show a pro-

cess of construction of sigmoid wavelet by the substi-

tution of the function s(x) by ϒ(qx) in the Equation 1.

So, the Equation 2 is the wavelet function created in

(Pati and Krishnaprasad, 1993).

ψ(x) = g(x+ r) −g(x −r) (2)

where r > 0. By terms of sigmoid function, the

Equation 2, ψ(x) is given by:

ψ(x) = ϒ(qx+ a+ r) −ϒ(qx −a + r)−

ϒ(qx+ a−r) + ϒ(qx −a −r) (3)

where q > 0 is a constant that control the curve of the

sigmoid function and α and r ∈ R > 0.

Pati and Krishnaprasad demonstrated that the

function ψ(x) satisﬁes the admissibility condition for

wavelets (Daubechies, 1992). The Fourier Transform

of the function ψ(x) is given by the Equation 4:

∞

−∞

ψ(x)e

−iwx

dx = −i

4π

sin(wα)sin(wr)

sinh(

πw

)

(4)

In particular, we accepted for analysis and prac-

tical applications the family of sigmoid wavelet gen-

erated by the parameters q = 2 and α = r, as exam-

ple. So, the Equation 3 can be rewritten the following

form:

ψ(x) = ϒ(2x+ m) −2ϒ(2x) −ϒ(2x−m) (5)

where m = α+ r.

Following, partially, this research line, we present

in the next section a technique for construction of

wavelets based on linear combination of sigmoid

powers.

HEALTHINF 2008 - International Conference on Health Informatics

100

3 POLYNOMIAL POWERS OF

SIGMOID

The Polynomial Powers of Sigmoid (PPS) is a class

of functions that have been used in recent years to

solve a wide range of problems related to image and

signal processing (Marar, 1997). Let ϒ : R → [0,1]

be a sigmoid function deﬁned by ϒ(x) =

1+e

−x

. The

−power of the sigmoid function is a function

: R → [0,1] deﬁned by ϒ

(x) =

1+e

−x

Let Θ be set of all power functions deﬁned by (6):

Θ = {ϒ

(x),ϒ

(x),..., ϒ

(x),...} (6)

An important aspect is that the power these functions,

still keeps the form of the letter S. Looking the form

created by the power functions of sigmoid, suppose

that the n

power of the sigmoid function to be repre-

sented by the following form:

(x) =

+ a

−x

+ a

−2x

+ ···+ a

−nx

(7)

where a

..., a

are some integer values. The

extension of the sigmoid power can be viewed like

lines of a Pascal

s triangle. The set of function writ-

ten by linear combination of polynomial powers of

sigmoid is deﬁned as PPS function. The degree of

the PPS is given by the biggest power of the sigmoid

terms.

3.1 Polynomial Wavelet Family on PPS

The derivative of a function f (x) on x = x

is deﬁned

by:

) = lim

∆x→0

f(x

+ ∆x) − f (x

)

∆x

since the limits there is. So, if we do the computation

of the Equation 8 :

f(x

+ ∆x) − f (x

)

∆x

(8)

for a small value of ∆x , showed have a good appro-

ximation for f

). Naturally, ∆x can be positive or

negative. So, if is we use negative value for ∆x, the

expression will be:

f(x

−∆x) − f (x

)

−∆x

(9)

This way, we can say that the arithmetic measure

of the Equations 8 and 9 will be a good approxima-

tion for f

) too. Then, we can write the following

Equation 10:

) '

f(x

+ ∆x) − f (x

−∆x)

2∆x

(10)

By convenience, we consider p = 2∆x and its su-

bstitution in the Equation 10. So, we have the Equa-

tion 11:

) '

f(x

) − f (x

−

)

(11)

this point we computed an approximated value for the

second derivative of f (x) in x = x

. From the Equa-

tion 11, changing f (x) by f

(x), we obtain the Equa-

tion 12 :

) '

) − f

−

)

(12)

reusing the Equation 11, we can write:

) '

f(x

+ p) − f (x

)

and

−

) '

f(x

) − f (x

−p)

using these results in the Equation12, we have an ap-

proximation of the second derivative of f(x) in x = x

that is given by:

) '

f(x

+ p) −2f (x

) + f (x

−p)

(13)

The approximation given by the Equation 13 is ex-

tremely adequate for the that f(x) is a sigmoid func-

tion. Suppose that f (x) is a sigmoid, for example,

ϒ(x). So, the second derivative of ϒ(x) is approxi-

mated by the Equation 14:

) '

ϒ(x

+ p) −2ϒ(x

) + ϒ(x

−p)

(14)

Due the fact of the sigmoid function to be continu-

ous and differentiable for any x ∈ R, we can say that

the Equation 14 is true for any x

, then we can write

the Equation 15, deﬁned for all x ∈ R.

(x) '

ϒ(x

+ p) −2ϒ(x) + ϒ(x − p)

(15)

Comparison the Equations 15 and 5, we do

there analysis for the approximation of the second

derivative of sigmoid function. The ﬁrst for values of

p ≥ 1 and the second for values of p < 1.

Case p ≥1:

HUMAN FACE VERIFICATION BASED ON MULTIDIMENSIONAL POLYNOMIAL POWERS OF SIGMOID (PPS)

101

It is clear that the function given by the sigmoid

second derivative approximation, Equation 15, also

will have the same form of the Pati and Krishnaprasad

functions, except of a p

constant that divides their

amplitude. So, the following result is true: when

p > 1 always there is a sigmoid wavelet which

integral of the admissibility condition (Daubechies,

1992) limited the same integral of the Equation 15.

Therefore, the approximation of the second derivative

of the sigmoid function is a wavelet too.

Case p < 1:

In this case, we will analyze when p is going to zero,

i.e.,

lim

p→0

+ p) −2ϒ(x) + ϒ

(x−p)

(16)

this limit tends to the second derivative of the function

is given on PPS terms by:

(x) = 2ϒ(x)

−3ϒ(x)

+ ϒ(x) (17)

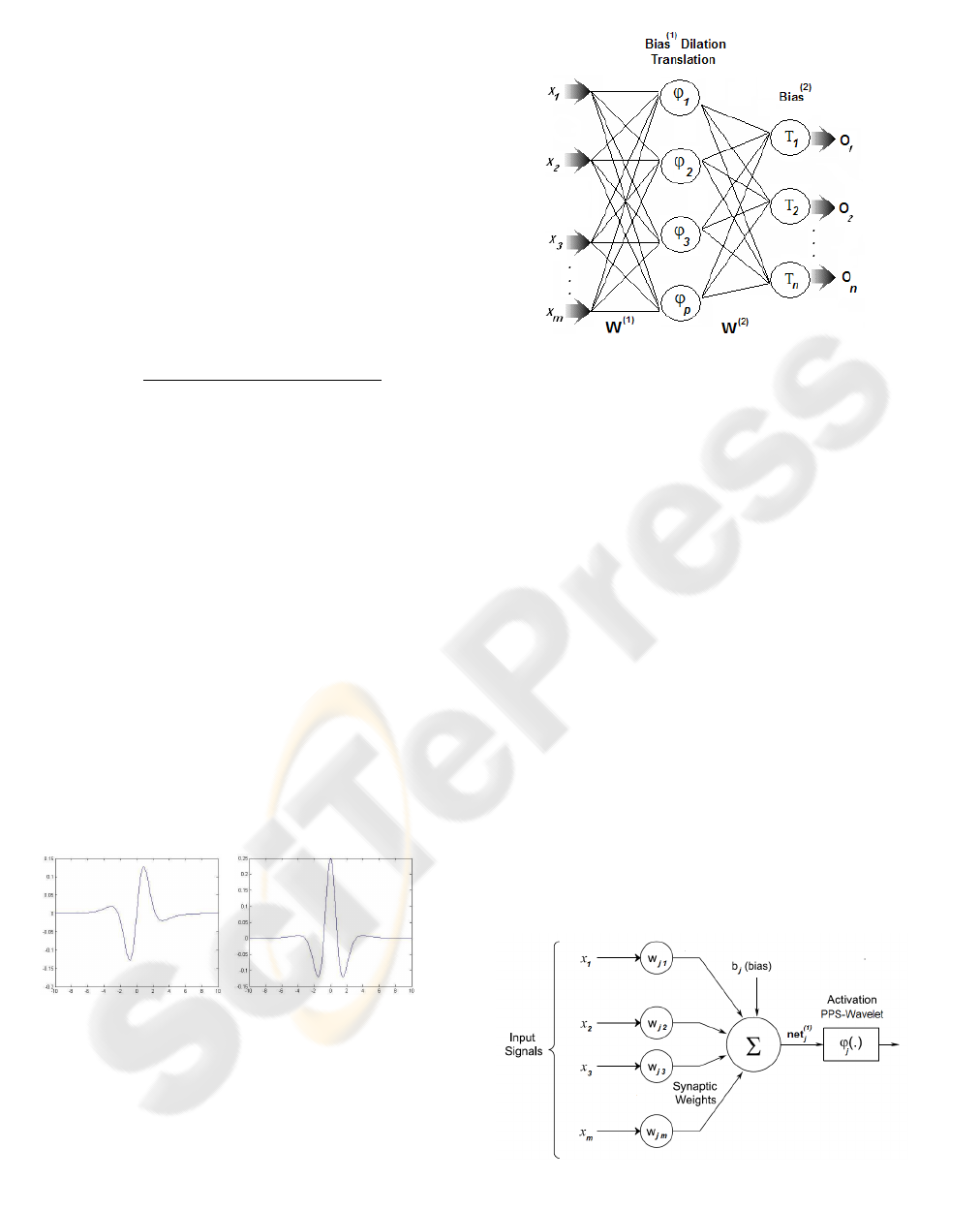
where we denominated ϕ

(x) the ﬁrst wavelet the

sigmoid function. The others derivatives, begin on

the second, we considered true by derivative proper-

ty by Fourier Transform (Marar, 1997). The suc-

cessive derivation process of sigmoid functions, al-

lowed to join a family of wavelets polynomial func-

tions. Among many applications for this family of

PPS-wavelets, special one is that those functions can

be used like activation functions in artiﬁcial neurons.

The following results correspond to the the analytical

functions for the elements ϕ

(x) and ϕ

(x) that are

represented by:

(x) = −6ϒ

(x) + 12ϒ

(x) −7ϒ

(x) + ϒ(x)

(x) = 24ϒ

(x) −60ϒ

(x) + 50ϒ

(x) −15ϒ

(x) + ϒ(x)

(x) ϕ

(x)

Figure 1: PPS-wavelets examples.

3.2 PPS Wavelet Neural Network

Let us consider the canonical structure of the multidi-

mensional PPS-wavelet neural network (PPS-WNN),

as shown in Figure 2.

Figure 2: PPS-wavelet neural network Architectures.

For the PPS-WNN in Figure 2, when a input pat-

tern X = (x

,... , x

)

is applied at the input of the

network, the output of the i

neuron of output layer is

represented as a function approximation problem, ie,

f : R

→ [0,1]

, given by:

(x) '

∑

j=1

(2)

∑

k=1

(1)

−b

(1)

−t

−b

(2)

(18)

where p is number of hidden neurons, ϒ(.) is sig-

moid function, ϕ(.) is the PPS-wavelet, w

(2)

are weight between the hidden layer to the output

layer, w

(1)

are weights between the input to the hid-

den layer, d are dilation factors and t are translation

factors of the PPS-wavelet, b

(1)

and b

(2)

are bias

factors of the hidden layer and output layer, respec-

tively.

Figure 3: The Hidden Neuron of PPS-Wavelet Neural Net-

work.

HEALTHINF 2008 - International Conference on Health Informatics

102

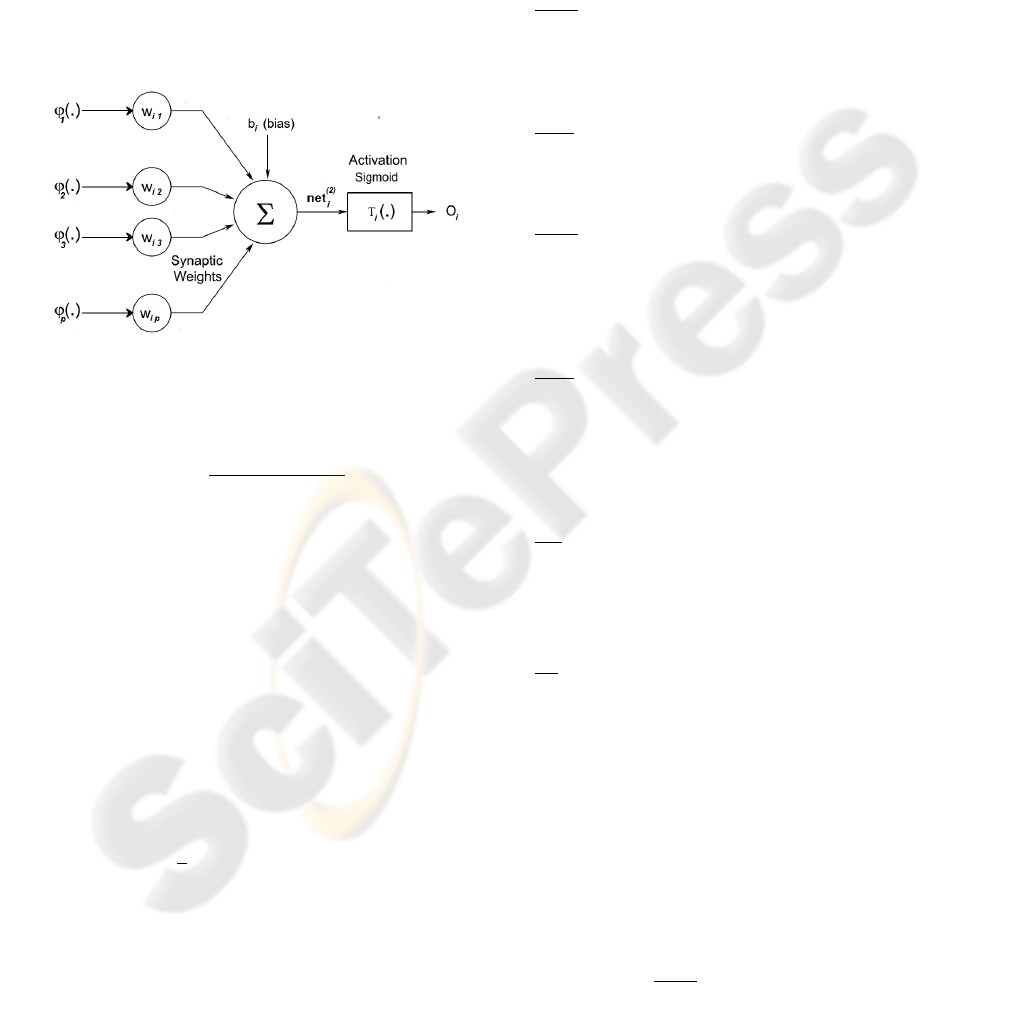
The PPS-WNN contains PPS-wavelets as the ac-

tivation function in the hidden layer ( Figure 3) and

sigmoid function as the activation function in the out-

put layer (Figure 4).

The output of the j

PPS-wavelet hidden neuron

(Figure 3) is given by :

= ϕ

.(net

(1)

−t

))

where

net

(1)

∑

k=1

(1)

−b

(1)

The output of the i

output layer neuron (Figure 4)

Figure 4: The Output Neuron of PPS-Wavelet Neural Net-

work.

is given by:

}

1+ exp(−net

(2)

)

where

net

(2)

∑

j=1

(2)

.(net

(1)

−t

)) −b

(2)

The adaptive parameters of the PPS-WNN consist

of all weights, bias, translations and dilation terms.

The sole purpose of the training phase is to determine

the ”optimum” setting of the weights, bias, transla-

tions and dilation terms so as to minimize the diffe-

rence between the network output and the target out-

put. This difference is referred to as training error of

the network. In the conventional backpropagation al-

gorithm, the error function is deﬁned as:

E =

∑

q=1

∑

i=1

−o

)

(19)

where n is the dimension of output space, s is the

number of training input patterns

The most popular and successful learning method

for training the multilayer perceptrons is the back-

propagation algorithm. The algorithm employs an

iterative gradient descendent method of minimization

which minimizes the mean squared error (L

norm)

between the desired output (y

) and network output

). From Equations (18) and (19), we could

deduce the partial derivatives of the error to each

PPS-wavelet neural network parameter

s, which is

given by:

Partial Equations of the Output Layer

∂E

∂w

(2)

= −

∑

q=1

−o

).o

.(1−o

.(net

(1)

q j

−t

)) (20)

∂E

∂b

(2)

∑

q=1

− o

).o

.(1 − o

) (21)

Partial Equations of the Hidden Layer

∂E

∂w

(1)

= −d

∑

q=1

[ϕ

.(net

(1)

−t

)).x

∑

i=1

−o

).o

.(1−o

).w

(2)

i j

] (22)

∂E

∂b

(1)

∑

q=1

[ϕ

.(net

(1)

q j

−t

)).d

∑

i=1

−o

).o

.(1−o

).w

(2)

i j

] (23)

Partial Equations of the PPS-Wavelet Parameters

∂E

∂d

∑

q=1

{[ϕ

.(net

(1)

−t

)).(net

(1)

q j

−t

)].

∑

i=1

−o

).o

.(1−o

).w

(2)

i j

} (24)

∂E

∂t

= d

∑

q=1

[ϕ

.(net

(1)

q j

−t

)).

∑

i=1

−o

).o

.(1−o

).w

(2)

i j

] (25)

After computing all partial derivatives the network

parameters are updated in the negative gradient direc-

tion. A learning constant γ deﬁnes the step length of

the correction, r is the iteration and momentum factor

is β. The corrections are given by:

(2)

i j

(r + 1) =

(2)

i j

(r) −γ.

∂E

∂w

(2)

i j

+ β.(w

(2)

i j

(r) −w

(2)

i j

(r −1))

HUMAN FACE VERIFICATION BASED ON MULTIDIMENSIONAL POLYNOMIAL POWERS OF SIGMOID (PPS)

103

(2)

(r + 1) =

(2)

(r) −γ.

∂E

∂b

(2)

+ β.(b

(2)

(r) −b

(2)

(r −1))

(1)

(r + 1) =

(1)

(r) −γ.

∂E

∂w

(1)

+ β.(w

(1)

(r) −w

(1)

(r −1))

(1)

(r + 1) =

(1)

(r) −γ.

∂E

∂b

(1)

+ β.(b

(1)

(r) −b

(1)

(r −1))

(r+ 1) = d

(r) −γ.

∂E

∂d

+β.(d

(r) −d

(r−1))

(r + 1) = t

(r) − γ.

∂E

∂t

+ β.(t

(r) −t

(r −1))

4 HUMAN FACE VERIFICATION

This study presents a system for detection and extrac-

tion of faces based on the approach presented in (Lin

and Fan, 2001), which consists of ﬁnding isosceles

triangles in an image, as the mouth and eyes form that

geometric ﬁgure when linked by lines. In order for

these regions to be determined, the images must be

converted into binary images, thus the vertices of the

triangles must be found and a rectangle must be cut

out around them so that their size can be brought to

normal and the area can be fed into a second part of

the system that will analyze whether or not it is a real

face. three different approaches are tested here: A

weighing mask is used to score the region, proposed

by Lin and Fan (Lin and Fan, 2001), a classical MLP

backpropagation (MLP-BP) and PPS-wavelet neural

network, for the analysis to be performed.

4.1 Image Treatment

First the image was read with the purpose of alloca-

ting a matrix in which each cell indicates the level of

brightness of the correspondent pixel; then, it is con-

verted into a binary matrix by means of a Threshold

parameter T, because the objects of interest in our case

are darker than the background. This stage changes

to 1 (white) a brightness level greater than T and to 0

(black). In most of the cases, due to noise and distor-

tion in the input image, the result of the binary trans-

formation can bring a partition image and isolated

pixels. Morphologic operations - opening followed

by closing - are applied with the purpose of solving

or minimizing this problem (Gonzalez and Woods,

2002). The Figure 5 shows the result of these oper-

ations.

Figure 5: Image treatment after morphologic operations.

XSegmentation of Potential Face Regions

After binarization the task is ﬁnding the center of

three 4-connected components that meet the follow-

ing characteristics:

1. vertex of an isosceles triangle (Lin and Fan,

2001);

2. the Euclidean distance between the eyes must be

90-100 % the distance between the mouth and

the central point between the eyes (Lin and Fan,

2001);

3. the triangle base is at the top of the image.

The last restriction does not allow ﬁnding upside

down faces, but it signiﬁcantly reduces the number

of triangles in each image, thus reducing the process-

ing time to the following stages. For example, the

numbers of triangles found in Figure 5(D), with this

restriction 399 and without restriction 769.

The opening and closing operations are vital,

since it is impossible to determine the triangles with-

out this image treatment. The processing mean time

HEALTHINF 2008 - International Conference on Health Informatics

104

to ﬁnd the results presented was 4 seconds; on the

other hand, 8 hours were insufﬁcient in an attempt at

ﬁnding the same results using a Pentium 4 with 2.4

Ghz processor in Figure 5(C).

XNormalization of Potential facial Regions

Once the potential face regions that we have selected

in the previous section are allowed to have different

sizes. All regions had to be normalized to the (60x60)

pixels size by bi-cubic interpolation technique, be-

cause every potential regions needs to present the

same amount of information for comparison. So, nor-

malization of a potential region can reduce the effects

of variation in distance and location.

4.2 Face’s Pattern Recognition

The purpose of this stage is to decide whether a poten-

tial face region in an image (the region extracted in the

ﬁrst part of the process) actually contains a face. To

perform this veriﬁcation, two methods were applied :

The weighting mask function, described by Lin and

Fun (Lin and Fan, 2001) and PPS-wavelet neural net-

work.

XThe Weighting Mask Function

The function Weighting Mask, according to the au-

thor, it is based on the following idea: If the nor-

malized potential region is really contains a face, it

should have high similarity to the mask that is formed

by 10 binary training faces (Mask Generation). Every

normalized potential facial region is applied into the

weighting mask function that is used to compute the

similarity between the normalized potential facial re-

gion and the mask. The computed value can be used

in deciding whether a potential region contains a face

or not.

Mask Generation

The mask was created using 10 images. The ﬁrst ﬁve

are pictures of females and the others are pictures of

males. All of them were manually segmented, bina-

rized, normalized, morphologically treated (opening

and closing) and then the sum of the correspondent

cell of each image was stored in the 11

matrix. Fi-

nally, that matrix was binarized with another Thresh-

old T, for which values lower than or equal to T were

replaced by 0, and the others by 1. The result was

improved with T=4. Whereas at lower values the ar-

eas of the eyes and mouth become too big, at higher

values these areas almost disappear. In both cases,

determining the triangles is considerably difﬁcult.

Weighting Mask Algorithm

The algorithm used to decide whether a potential face

(R) contains a real face is based on the idea that the

binary image of a face is highly similar to that of the

mask.

Begin

Input the region R and mask M; p=0;

For all pixels of R and M

IF the pixel from R and M is white

Then p = p+6;

IF the pixel from R and M is black

Then p = p+2;

IF the pixel from R is white and that from M is

black

Then p = p - 4;

IF the pixel from R is black and that from M is

white

Then p = p - 2;

End

A set experimental results demonstrates that

the threshold values should be a set between face

3400<= p >= 6800 (Marar et al., 2004).

XPPS-wavelet Neural Network

In order to demonstrate the efﬁciency of the proposed

model. Two PPS-WNNs, one with the activation

function ϕ

(.) and the other with ϕ

(.) in the hidden

layer, were implemented to analyze when a potential

face region really contains a face. However, the raw

data face, (60 x 60) pixels, cannot be used directly

for the training the networks because the features are

deep hidden. Therefore, we used the Principal Com-

ponents Analysis (PCA) method to create a face space

that represents all the faces using a small set of com-

ponents (Marar, 1997). For this purpose we consider

the ﬁrst 15 components as the extracted features or

face space. In that case study, 100 manually seg-

mented faces (50 women and 50 men) and more 40

non-face random images were used to network train-

ing.

Therefore, the PPS-WNNs and classical MLP-BP

architectures with 15 units in the input layer, with 16

PPS-wavelet neurons in the hidden layer and with 2

neurons in the output layer were designed and trained.

Here, in the output layer, we represented face by the

vector (1,0) and non-face by the vector (0,1). We

used, as test, the same regions (R) applied to the pre-

vious method.

HUMAN FACE VERIFICATION BASED ON MULTIDIMENSIONAL POLYNOMIAL POWERS OF SIGMOID (PPS)

105

5 RESULTS

Several tests were performed to determine an ideal

threshold value for the conversion of the images into

binary ﬁgures. In a scale from 0 (black) to 1 (white),

0.38 was empirically determined as a good value to

most of the images, but to darker images 0.22 was a

better value. The test was done through the use of

100 images (50 male and 50 female) with two differ-

ent threshold values from (Department, 2003). The

results are shown in Table 1.

Table 1: Face veriﬁcation results with 2 threshold values.

Threshold 0.22 0.38

Weighting Correct Detection 81 % 48 %

Mask False Detection 25 % 21 %

Classical Correct Detection 83 % 35 %

MLP-BP False Detection 28 % 17 %

PPS-WNN Correct Detection 85% 63 %

(.) False Detection 15 % 23 %

PPS-WNN Correct Detection 92 % 51 %

(.) False Detection 5 % 11 %

The best result for T=0.22 is explained by the low

brightness and consequently low contrast of the im-

ages in the set. All the images used are at an 8 bit

gray scale and 540 x 640 pixels. All tests were per-

formed in an IBM -compatible PC, Pentium 4 with

2.4 Ghz processor, 1Gb RAM memory.

6 CONCLUSIONS

The face recognition is an active research area for se-

curity. However, it is still a complex and challenging

research topic because the human face may change its

appearance due to the internal variations such as facial

expressions, beards, mustaches, hair styles, glasses,

ageing, surgery and the external distortions such as

scale, lighting, position and face occlusion. In this

paper, we showed the basic concepts and technics of

Polynomial Powers of Sigmoid and how to build mul-

tidimensional wavelet neural networks starting from

this deﬁnition. We chose this application due to the

complexity of image processing problems. The ob-

tained results suppose to validate the new method for

new and future applications in the artiﬁcial intelli-

gence area.

ACKNOWLEDGEMENTS

We would like to thank the Coordenac¸

ao de

Aperfeic¸oamento de Pessoal de N

ıvel Superior

(CAPES) process number 3634/06 −0 and the Lis-

bon University that supported this investigation.

REFERENCES

Avci, E. (2007). An expert system based on wavelet neural

network-adaptive norm entropy for scale invariant tex-

ture classiﬁcation. Expert Systems with Applications,

32:919–926.

Daubechies, I. (1992). Ten lecture on wavelets. Society for

Industrial and Applied Mathematics (SIAM).

Department, P. (2003). Psycological image collection at

stirling university. http://pics.psych.stir.ac.uk.

Fan, J. and Wang, X. F. (2005). A wavelet view of small-

world networks. IEEE Transactions on Circuits and

Systems, pages 1–4.

Funahashi, K. (1989). On the approximate realization of

continuos mappings by neural networks. Neural Net-

works, (2):183–192.

Gonzalez, R. C. and Woods, R. E. (2002). Digital Image

Processing. Prentice-Hall, Inc.

Jiang, X., Mahadevan1, S., and Adeli, H. (2007). Bayesian

wavelet packet denoising for structural system identi-

ﬁcation. Struct. Control Health Monit., 14:333–356.

Lin, C. and Fan, K.-C. (2001). Triangle basead approuch to

detection of human face. Pattern Recognition Society,

pages 941–944.

Marar, J. F. (1997). Polinomios Pot

encias de Sigmoide

(PPS): Uma nova T

ecnica para Aproximac¸

ao de

Func¸

oes, Construc¸

ao de Wavenets e suas aplicac¸

oes

em Processamento de Imagens e Sinais. PhD thesis,

Universidade Federal de Pernambuco - Departamento

de Inform

atica.

Marar, J. F., Costa, D., Pinheiro, O., and Filho, E. (2004).

Adaptative techniques for the human faces detection.

In 6th International Conference on Enterprise Infor-

mation Systems, volume 2, pages 465–468.

Misra, B. B., Dash, P. K., and Panda, G. (2007). Pattern

classiﬁcation using local linear wavelet neural net-

work. International Conference on Information and

Communication Technology, pages 92–95.

Oussar, Y. and Dreyfus, G. (2000). Initialization by se-

lection for wavelet neural traing. Neurocomputing,

34:131–143.

Pati, Y. and Krishnaprasad, P. (1993). Analysis and syn-

thesis of feedforward neural networks using discrete

afﬁne wavelet transformations. IEEE Transactions on

Neural Networks, 4(1):73–85.

Zhang, H. and Pu, J. (2006). A novel self-adaptive control

framework via wavelet neural netwok. In 6th World

congress on intelligent control and automation, pages

2254–2258.

HEALTHINF 2008 - International Conference on Health Informatics

106