
BIOMIMETICS AND PROPORTIONAL NOISE IN MOTOR
CONTROL
Christopher M. Harris
Centre for Theoretical and Computational Neuroscience, Universityv of Plymouth, Plymouth, Devon PL4 8AA, U.K.
Keywords: Human movement, optimal control, minimum variance, minimum jerk, channel capacity, neuromorphic
engineering, biomimicry, size principle, saccade, arm reaching.
Abstract: Proportional noise, in which the standard deviation of signal noise is proportional to signal mean, is a
fundamental constraint on human motor performance but why it occurs is unknown. We show that for
neural networks with binary thresholded units, channel capacity is maximised with a recruitment strategy
that produces PN. The size principle also emerges, in agreement with observation. We therefore argue that
Fitt’s law, speed-accuracy trade-off, and the minimum variance trajectories (including minimum jerk
trajectories for limiting brief movements), which are observed in most human point-to-point movements,
have evolved as optimal strategies resulting from maximising channel capacity. We conclude that
biomimicry of minimum variance and minimum jerk trajectories in robotics is probably only of aesthetic
value when using standard technology. In contrast, biomimicry using neuromorphic technology in which
networks are built from stochastic silicon ‘neurons’ with thresholds, is functional biomimetics and
optimization of channel capacity will produce behaviours that are human-like.
1 INTRODUCTION
A fundamental tenet of biomimetics is that naturally
occurring systems have intrinsically ‘good’ qualities.
By mimicking natural systems, it is believed that
these qualities will transfer to synthetic systems.
While there are some positive examples (eg. ‘gecko
tape’ Geim et al, 2003), it is not always obvious
what true benefits accrue from biomimicry, and
building copies of nature may become an aesthetic
end in itself. Natural systems evolve and adapt to
solve problems of survival and reproduction, often
by optimizing performance and structure within a
particular environment or constraint. Mimicking the
behaviour or structure without understanding the
natural constraints may not be beneficial and may be
quite suboptimal if the context/constraints are not
relevant to the synthetic system. To translate
nature’s solutions to synthetic systems requires a
scientific understanding of the problem nature is
attempting to solve.
Mimicking human movements in robots is a
particularly pertinent example. It is well-known that
human movements that redirect an effector (limb,
eye, etc.) from one point to another in space, such as
reaching or saccadic eye movements, are highly
stereotyped with characteristisc ‘smooth’
trajectories. For brief (rapid) movements, velocity
profiles tend to be symmetrical, ‘bell-shaped’ and
rather straight. Historically, this behaviour was first
captured by the ‘minimum jerk’ trajectory (MJ)
(Hogan, 1984; Flash & Hogan 1985) which
purported to show that observed trajectories
minimised the square of jerk (derivative of
acceleration) integrated over the movement duration.
It was argued that the MJ trajectory was a maximally
‘smooth’ trajectory. Subsequently, the MJ has been
mimicked as a control objective in numerous robotic
systems, presumably because of the smoothness
performance (it is also easy to compute). However,
from a biological viewpoint, the MJ hypothesis has
been criticised because of the lack of plausibility of
smoothness as a biological relevant performance
criterion. Much smoother trajectories are feasible
(Harris, 2004) and the MJ model cannot explain why
longer movements have asymmetrical velocity
profiles. So why build robots with MJ trajectories? –
is it aesthetic biomimicry or does it build ‘good’
robots?
A more recent optimal control model of human
movement is the minimum variance model (MV)
(Harris & Wolpert, 1998) in which it is proposed
that trajectories minimise the inaccuracies caused by
37
M. Harris C. (2008).
BIOMIMETICS AND PROPORTIONAL NOISE IN MOTOR CONTROL.
In Proceedings of the First International Conference on Bio-inspired Systems and Signal Processing, pages 37-43
DOI: 10.5220/0001057100370043
Copyright
c
SciTePress
proportional noise (PN), which is a specific kind of
signal-dependent noise where the standard deviation
of noise on a signal is proportional to the mean of
the signal.
Kx
x
=
σ
(1)
where K is a constant. The MV model captures
many features of observed trajectories including
increasing asymmetry with duration and the
ubiquitous Fitt’s law (see below). In this model,
‘smoothness’ is a by-product - not an objective - of
the optimization because rapid changes in effector
position cause more output variance. We are now
beginning to see the incorporation of MV objectives
in robotic systems (Simmons & Demiris, 2005).
Again though, why build robots with MV
trajectories? – is it biomimicry for its own sake, or
does it build ‘better’ robots?
There is no doubt (mathematically) that the
‘smoothness’ cost function is a by-product of the PN
constraint, but why does PN occur in natural
systems? Indeed is PN optimal itself for some
deeper constraint, and for roboticists is this deeper
constraint even relevant to robotics? This is the
question we wish to address.
Human movement appears to be tightly
constrained by the effects of PN. Most point-to-point
movements (such as arm reaching) can be described
by the empirical Fitt’s law in which the duration of a
movement depends only on the ratio of target
distance to target width. This invariance implies that
that the standard deviation of end-point error is
proportional to target distance (ie. PN).
Physiological measurements have confirmed the
existence of PN in isometric force production
(Schmidt et al., 1979; Jones et al, 2002). For low-
pass systems (such as muscles), PN on the input
command leads directly to a speed-accuracy trade-
off. Faster transitions at the ouput require more
intense commands which are noisier because of PN,
which in turn lead to greater end-point error. For a
given muscle plant, there is a unique trajectory that
minimises end-point variance (for a given duration)
which has been shown to be in close agreement with
the observed bell-shape velocity profiles (Harris &
Wolpert, 1998, 2006).
It is important to distinguish PN from the noise
encountered in renewal point processes (eg. Poisson
process), which we call Renewal Noise (RN). The
firing rate of neurons has often been modelled as a
renewal point process, but in RN it is the variance
that is proportional to the mean rate, where the
constant of proportionality (Fano factor F) depends
on the inter-spike interval distribution:
()
2/1
Fx
x
=
σ
(2)
PN does not emerge as a ‘natural’ property of a
renewal process (Harris, 2002). Simple mixing of
renewal processes does not produce PN, but tends to
produce an ever more Poisson-like renewal process
(Cox & Miller, 1977). PN must emerge in some
other way.
In this paper, we consider an idealised motor
recruitment network, or ‘channel’, and show
analytically that there is an optimal recruitment
strategy to maximise the number of signals that can
be transmitted for a given error probability. PN
emerges as the optimal noise for binary sub-
channels. We then consider the implications for
dynamic motor control.
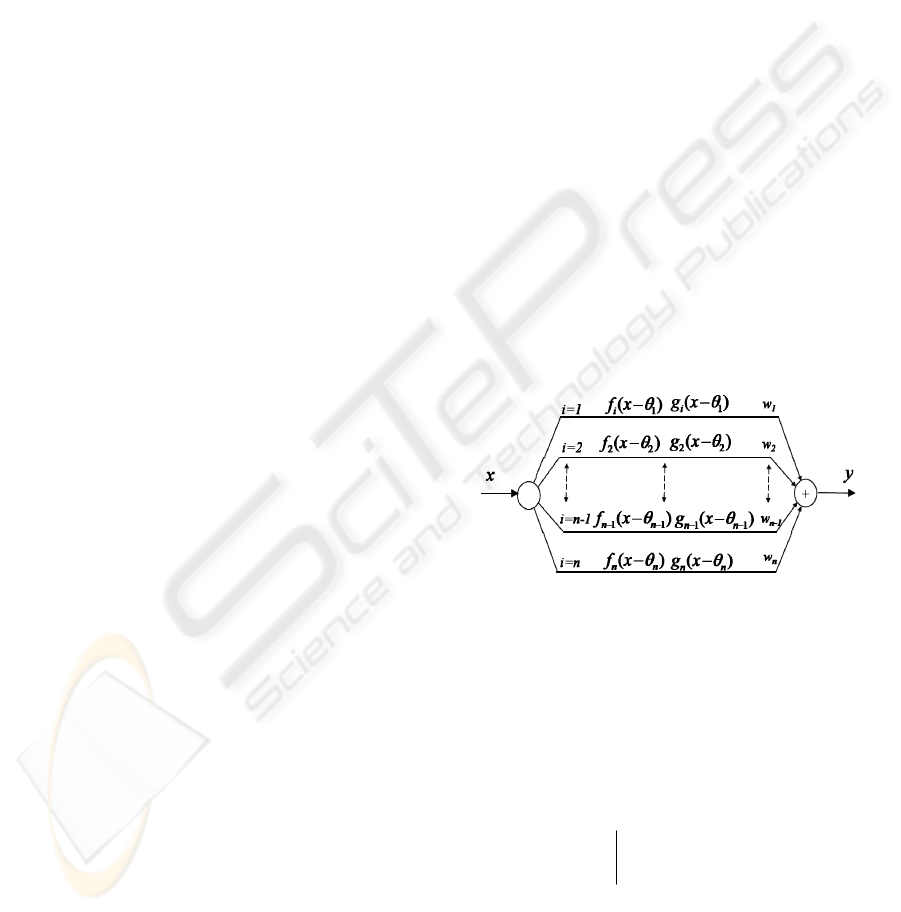
2 THE IDEALISED CHANNEL
The idealised recruitment channel consists of a
parallel network of a large number of noisy sub-
channels (eg. motor neurons) each driven by the
same input,
)(tx . The channel output, )(ty , is a
linear weighted sum of the sub-channel outputs
(fig.1).
Figure 1: An idealised recruitment channel.
Each sub-channel has a thresholded response
function, so that when the instantaneous value of the
input exceeds the threshold of the sub-channel, the
sub-channel is switched on and generates a noisy
signal. When the input is below threshold, the sub-
channel is switched off and generates no output and
no noise. We denote the output of the ith sub-
channel (
Ni ,1
=
) by
i
iii
i
tx
txtxf
tz
θ
θθ
<
>−
=
)(0
)())((
)(
(3)
where
(.)
i
f denotes the response characteristic of the
ith sub-channel, and
i
θ
is a constant threshold for
that sub-channel.
Each sub-channel generates noise when switched
on, which we assume to be mutually independent
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
38

from the noise of any other channel. We denote the
instantaneous noise variance at the output of each
sub-channel by:
i
iii
i
tx
txtxg
t
θ
θθ
σ
<
>−
=
)(0
)())((
)(
2
(4)
where
(.)
i
g denotes how noise variance depends on
the sub-channel input. The output of the whole
channel is then given by
∑
=
=
N
i
ii
tzwty
1
)()(
(5)
where
i
w is a fixed positive weight. The total output
variance is given by
∑
=
=
N
i
ii
twtv
1
22
)()(
σ
(6)
We assume that
(.)
i
f and (.)
i
g are pre-specified
functions determined by the characteristics of the
sub-channels. For convenience, we drop the time
dependence and consider only steady-state responses
(we will return to the dynamic case later).
Because of the redundancy in the system, it is
obvious that there are many ways we can generate a
specified output value, y, for a given input value x,
by suitable choice of weights and thresholds.
However, in general, each way will produce a
different
)(tv . Therefore, our goal is to find the
distribution of weights and thresholds that optimises
)(tv according to some cost function. To do this we
develop the problem using continuous functions to
allow us to use variational calculus to find the
optimal weights and thresholds.
2.1 Continuous Recruitment Equations
We approach this problem analytically by assuming
that there are a large number of sub-channels so that
we can approximate summations in equations 5 and
6 with integrals. In anticipation of a possible
singularity occurring at
0
=
x , we also assume that
the input can range only over
max
xx ≤≤
ε
where
ε
is
a small positive constant
max
0 x<<≤
ε
. We next
assume that there is a ‘density’ of units with
thresholds
x=
θ
denoted by )(x
ρ
, which is
constrained by:
∫
=
max
)(
x
dxxN
ε
ρ
(7)
The weights of sub-channels are approximated by
the continuous function
)(xw . The output can then
be written as a convolution integral:
∫
−=
′
x
x
dxxxfxxwxy
ε
ρ
)'()'()'()(
(8)
Where
(.)
x
f is the response characteristic of
subchannels with threshold at x. The output variance
is similarly:
∫
−==
′
x
xy
dxxxgxxwxxv
ε
ρσ
)'()'()'()()(
22
(9)
2.2 Channel Capacity
We now consider how to optimise the channel’s
performance when the expected value of channel
output is required to follow the input (ie. a unity gain
linear channel).
maxmax
)( xxxyxxy ≤≤
≤
≤
=
ε
ε
(10)
The channel is required to transmit signals of
different values at different times. We assume that
these signal values are uniformly distributed over the
range
max
xx
≤
≤
ε
, and that the channel is
memoryless with no expectation of which signal is
to be transmitted.
We consider the input to be deterministic, so that
the noise perturbing the output is due to the internal
noise of the recruited sub-channels, which we
assume to be Gaussian. Let us now assume that we
wish to transmit M signals spread across the range.
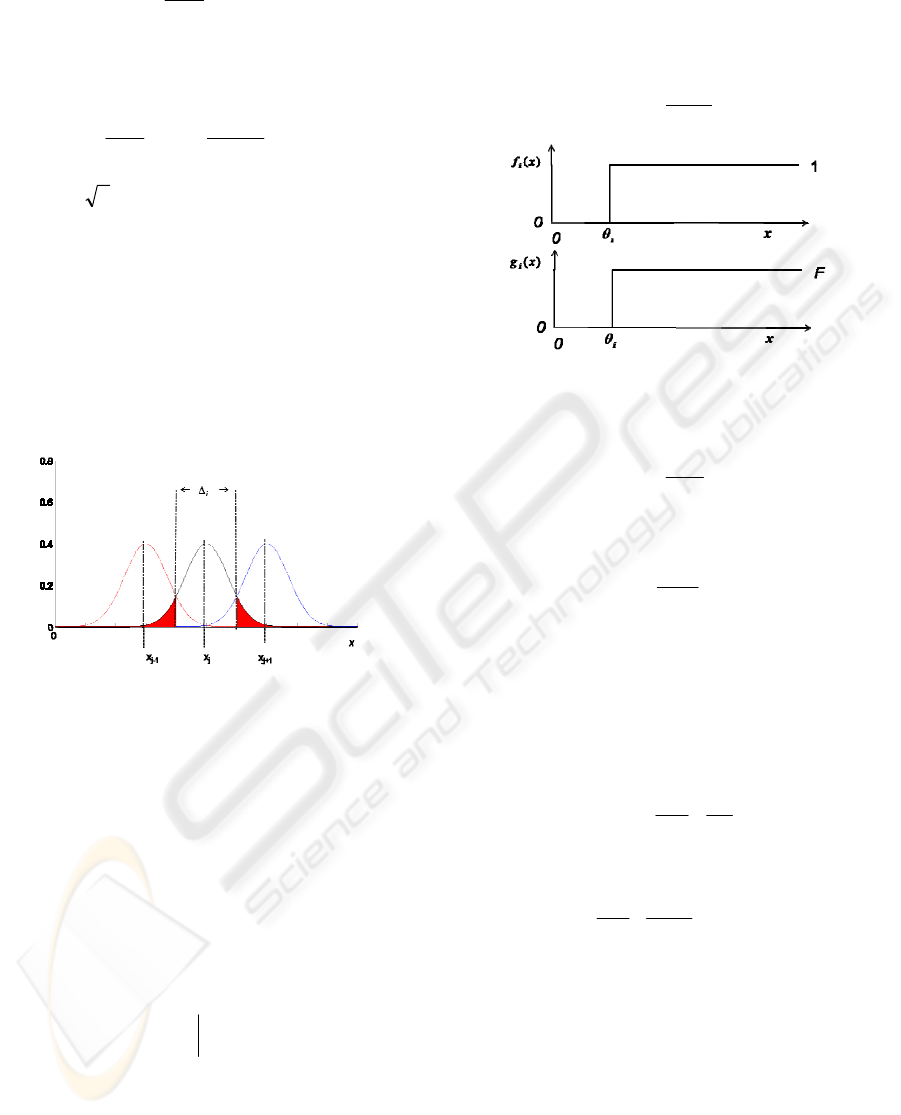
Consider three adjacent input signals,
1−j
x ,
j
x
1+j
x
(fig.2). We can see that the output
y given
j
x
could deviate sufficiently from the expected value
)(
j
xy
such that a maximum likelihood detector
could make an error by attributing the output to be
more likely to arise from
1−j
x
or
1+j
x
(shaded tails
in fig.2). Assuming noise variance changes slowly
with x, then the probability of the detector being
correct is
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
Δ
≈
i
y
i
c
erfp
σ
2
(11)
where
i
Δ
is the width of the region of correct
response. We argue that, of all the possible channel
configurations, the one that maximises the number
of signals that can be transmitted for a specified
probability of correct detection per signal is the best
configuration.
Assuming
i
Δ
to be small so that we can
make a continuous approximation, the number of
signals that can be transmitted is:
BIOMIMETICS AND PROPORTIONAL NOISE IN MOTOR CONTROL
39
∫
Δ
≈
max
)(
1
x
dx
x
M
ε
(12)
It follows from eq.11 that for a fixed probability of
correct response, we need to maximise the benefit
function
∫∫
=≈
maxmax
)(
)(
2/1
xx
dx
xv
b
dx
x
b
M
εε
σ
(13)
where
)(/2
1
c
perfb
−
= . This optimization is,
however, constrained by the channel’s possible
output variance functions, eq(9), which are
determined by the weighting function
)(xw and the
threshold density function
)(x
ρ
which must also
yield the desired output
)(xy
according to eq.10.
Finally the density function must also be constrained
by the total number of sub-channels according to
eq.7. We solve this is variational problem
analytically for simple binary sub-channels.
Figure 2: Output of subchannels for deterministic input.
3 BINARY CHANNELS
We now consider a ‘neuromorphic’ example in
which each sub-channel is a ‘neuron’ with an output
signal given by a spike train with a mean firing rate
of unity. We assume that the spike-train is a renewal
point process so that its variance is proportional to
the mean according to eq.2. We further assume that
when the neuron is switched on, the mean firing rate
does not change with increasing input, ie, the neuron
response function is a step function (see figure 3).
θ
θ
θ
<
>
=−
t
t
tu
0
1
)(
(14)
The recruitment equation (8) then simplifies to:
∫∫
′′′
=
′′
−
′′
==
xx
xdxxwxdxxuxxwxy
εε
ρρ
)()()()()(
(15)
which has the solution
1)()( =xxw
ρ
(16)
The variance will be given by:
2
() ()()
x
vx F w x x dx
ε
ρ
′′′
=
∫
(17)
or
∫
′
=
x
xd
x
Fxv
ε
ρ
)'(
1
)(
(18)
Figure 3: Binary sub-channel. Signal and variance are
step-functions.
Differentiating we have
)(
)(
xv
F
x
′
=
ρ
(19)
where the dash means the derivative with respect to
x. Substituting into eq.7, we have the constraint:
∫
′
=
max
)(
x
dx
xv
F
N
ε
(20)
3.1 Isoperimetric Problem
We recognise that maximising the benefit function
(eq.13) subject to the integral constraint (eq.20)
forms an isoperimetric problem in variational
calculus. The Lagrangian is:
v
F
v
b
vvxL
′
+=
′
λ
2/1
),,(
(21)
where
λ
is a constant Lagrange multiplier. The
Euler-Lagrange equation is
()
0
4
32/3
=
′
′′
−
v
vF
v
b
λ
(22)
which has the solution of the form
(
)
2
)( Kxxv =
(23)
where K is a positive constant. This is a maximum
and for positive
v
′
it satisfies the Weierstraussian
condition for a strong extremum (not shown here).
Since we have
x
y
=
, we can write the output
variance as
(
)
2
Kyv =
(24)
which is proportional noise.
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
40

3.2 Singularity
The threshold density function can now be found by
substituting eq.23 into eq20:
xK
F
x
2
2
)( =
ρ
(25)
which will require an infinite threshold density at the
origin. This is not physically realizable, so we
consider
max
0 x<<<
ε
. In this case we see from
eq.20 that
⎟
⎠
⎞
⎜
⎝
⎛
=
ε
max
2
ln
2
x
N
K
F
(26)
Thus it appears that we can come arbitrarily
close to the origin if we are willing to devote a large
enough number of channels. It also appears from
eq.25 that reducing K, is very expensive in sub-
channels since
⎟
⎠
⎞
⎜
⎝
⎛
=
ε
max
2
ln
x
K
N
F
(27)
As a numerical example, consider
ε
to be 0.1% of
max
x , then if we used a N=1000 sub-channels, then
K~0.06 for a Poisson sub-channel renewal process
(F=1).
An important property of this optimization is that
a size principle emerges. From eq.25 we see that the
number of sub-channels deceases with increasing
output, but from eq.16 we have
F
xK
x
xw
2
2
)(
1
)( ==
ρ
. (28)
The weights (or strengths) increase with increasing
signal. In human movement physiology, the size
principle is a well-known phenomenon, but we see
that it an inevitable emergent property of optimizing
the channel.
Thus far we have only considered positive
signals. To handle signals of either sign, we employ
two channels of different polarities with a common
origin, so that:
xK=
σ
(29)
We note that there are other configurations in which
the two channels could be active simultaneously by
having shifted origins (co-activation). This could
overcome problems with the singularity, but we do
not explore this here.
4 DYNAMICS
We now consider the dynamics of the optimal
channel. We will only give an outline to emphasise
some remarkable emergent properties, as some
aspects have already been dealt with in depth
elsewhere and others have yet to be explored
experimentally.
4.1 Fano Factor and Bandwidth
It can be seen from above, that the resources needed
for the optimal channel also depend on the Fano
factor F of the sub-channels. Thus fewer sub-
channels are needed if we can reduce F (eq.26).
However, for spike trains, reducing F comes at a
price, since it reduces bandwidth.
So far we have dropped the dependence on time.
Indeed, the above derivation is independent of time
provided there are no bandwidth restrictions on the
sub-channel response characteristics. However, for
the neuromorphic embodiment of sub-channels, the
output
)(tz
i
depends on the firing rate of a motor
neuron (sub-channel). Modelling the motor neuron
spike train as a renewal point process, the response
of
)(tz
i
will therefore depend on the inter-spike
interval probability distribution. For exponential
interval distributions, the rate process is Poisson
(F=1) with an autocovariance given by a delta
function. Thus a Poisson process yields a fast
temporal response, but requires a high F. In fact
motor neuron firing rates are not Poisson, but have
considerable lower Fano factors. This will result in a
broader autocovariance function and hence more
sluggish impulse response function (Cox & Miller,
1977). The relationship between the impulse
response function and the spike-interval distribution
is complex and non-stationary, so we will
approximate it by a first-order impulse response
function with a time-constant
τ
:
τ
τ
/)(
/t
z
etR
−
= (30)
4.2 Linear Plant Considerations
Assume that we use our optimal channel to drive a
physical effector plant, such as a real muscle, a
robotic arm, a prosthetic limb, etc.. We approximate
the plant as linear 2
nd
-order with mass/inertia,
viscosity, and elasticity. The drive to this plant is the
output of our channel,
)(ty which is not only
perturbed by PN, but also has its own dynamics
because of the non-Poisson statistics of the firing
rates. We must therefore consider an augmented
plant with a higher order, which will be at least 3
rd
order (given eq.31) (fig.4).
BIOMIMETICS AND PROPORTIONAL NOISE IN MOTOR CONTROL
41

Figure 4: Simplified lumped linear model of a motor
system driven by the optimized recruitment channel. The
channel generates a drive with PN which then is passed to
a 3
rd
order system including the response function of the
motor neuron renewal process and the actual 2
nd
order
effector plant.
Denote the augmented plant impulse response by,
)(tp with Laplace transform given by:
)1)(1)(1(
1
)(
21
+++
=
sTsTs
sP
τ
(31)
Then the variance at the output of the plant is given
by the convolution (Harris 1998):
tdttptxKt
t
o
′′
−
′
=
∫
0
2222
)()()(
σ
(32)
Note that the kernel is the square of plant impulse
response, and causes the variance response to be
more sluggish (and less intuitive) than the signal
response.
4.3 Optimal Trajectories
PN and its transfer through a linear system (eq.33)
has far reaching implications when we are required
to move an effector from one point to another, as in
reaching or saccadic eye movements. If we want to
move more quickly then we clearly need a larger
input signal,
)(tx but this will lead to a larger output
variance and hence larger pointing errors (end-point
errors). Conversely, if accuracy is important then the
input needs to be small and the movement will take
a longer time. The speed-accuracy trade-off implies
that for a given movement duration, there is a unique
trajectory (velocity profile) that minimises end-point
error. This has been found numerically and
analytically (Harris & Wolpert 1998, 2006). In two
dimensions trajectories tend to be straight.
For very brief movements, a 3
rd
order system
becomes dominated by the 3
rd
derivative (jerk) and
the kernel in eq. 33 tends towards the square of jerk.
Thus the variance at the end of the movement is
given by:
td
td
tod
KT
T
T
o
′
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
′
′
⎯⎯→⎯
∫
→
0
2
3
3
2
0
2
)(
)(
σ
(33)
Minimising jerk is therefore minimising variance in
the limit for a 3
rd
order system. However, this is only
approximate for brief movements. Careful analysis
of data using Fourier analysis reveals that arm
reaching and saccades are not MJ but closer to MV
(Harris & Harwood, 2005; Harwood et al., 1999).
For longer movements velocity profiles become
quite asymmetric and cannot be fit by the MJ model.
In summary, a vast amount of human goal-
directed dynamic motor behaviour is explicable as
an optimal trade-off between speed and accuracy,
which a direct result of PN. Perhaps most
remarkable, is that this can all be attributed to
maximising channel capacity!
5 DISCUSSION
If we start with a collection of noisy binary sub-
channels (units) with thresholds, then the optimal
pattern of threshold levels and weights is to recruit
sub-channels according to equations 25 and 28. This
arrangement maximises the number of different
signals we can transmit for a given error probability
per signal. It emerges that the output signal of such a
configuration exhibits proportional noise (PN)
(eq.1). This result is consistent with known
neurophysiology which has shown that PN emerges
from the orderly recruitment of motor units in
human arm movements (Jones et al, 2001). The
configuration of thresholds and weights is also
consistent with the well-known empirical size
principle in which stronger motor units are recruited
at higher thresholds. We have only considered
binary sub-channels, but it appears that a similar
result could occur for other types of rapidly
saturating sub-channels away from the origin (not
shown here). We propose, therefore, that PN is itself
is an optimal strategy that has evolved to maximise
channel capacity.
Once PN has emerged, it places a trade-off
between speed and accuracy for point-to-point
movements, which leads to an optimal trajectory
(the minimum variance trajectory), which fits
observations remarkably well (Harris & Wolpert
1998). For brief movements, the MV trajectory
becomes bell-shaped and similar to (but not exactly
the same as) the minimum jerk (MJ) profile. This is
why the MJ trajectory seems to fit observation quite
well (but only for brief movements).
Our overall conjecture is that through
evolution/adaptation multiple noisy sub-channels
with thresholds will ultimately and inevitably lead to
smooth straight movements.
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
42

5.1 The Biomimetic Question
Clearly we could build synthetic systems (robots
etc.) that mimic the smooth straight trajectories
made by humans simply because they look like
human movements. This is aesthetic biomimicry.
Incorporating minimum jerk (MJ) trajectories in
robots is probably as example of this kind of
mimicry. It could be argued that smoothness is
useful in reducing wear-and-tear, but there are much
smoother trajectories than MJ (Harris, 2004). One
would need to trade-off the cost of wear-and-tear
against poor dynamic performance. In any case,
human movements are not MJ, and are much better
described by minimum variance (MV) trajectories in
which PN inaccuracies are optimally traded against
duration. MJ trajectories are just a limiting case of
MV trajectories for brief durations. But copying
human trajectories, albeit more precisely with MV
profiles, is still aesthetic mimicry unless PN exists in
the synthetic system.
In contrast to aesthetic mimicry, functional
biomimetics copies the control objective of human
movement and incorporates it into the constraints in
the synthetic system. For example if the control
signal in a synthetic system were perturbed by
stationary additive Gaussian noise, making an
accurate and rapid movement would probably be
achieved by a bang-bang control solution. It only
makes sense to incorporate an MV controller if the
synthetic control signal is perturbed by PN, which in
our experience, is not common in conventional
engineered systems. One could, of course, introduce
PN deliberately, but this would just be aesthetic
mimicry.
5.2 The Neuromorphic Approach
Building synthetic systems with artificial neurons is
a fundamentally different proposition.
Neuromorphic technology can now produce silicon
neurons with thresholds and stochastic spike trains.
When configured optimally for movement control,
they should produce PN because, as we have shown
here, PN emerges at the output of the optimal
channel (at least for binary channels). For robots
built on this technology, MV trajectories would be
an optimal solution for speed and accuracy. This is
functional rather than aesthetic biomimetics.
But, why should synthetic systems employ
artificial neurons? Is this not just another level of
aesthetic mimicry? We suggest that the
neuromorphic argument runs deeper. Over eons,
biological functions and
structures have improved
survival through natural selection. Optimal solutions
to problems emerge (without mathematical premise)
that are not obvious to us, and not even achievable
with current technology. In the case of neural
systems, it is only by building them
neuromorphically, that we can discover these
solutions.
REFERENCES
Fitts P.M. (1954) The information capacity of the human
motor system in controlling the amplitude of
movement. Journal of Experimental Psychology 47:
381– 391.
Cox, D.R. Miller, H.D. (1977) The theory of stochastic
processes. Chapman & Hall, London.
Flash, T., Hogan N. (1985) The coordination of arm
movements: an experimentally confirmed
mathematical model. Journal of Neuroscience 5:
1688–1703, 1985.
Geim A.K., Dubonos S.V., Grigorieva I.V. et al. (2003)
Microfabricated adhesive mimicking gecko foot-hair
Nature Materials 2: 461-463
Hogan N. (1984), An organizing principle for a class of
voluntary movements, Journal of Neuroscience 4,
2745-2754.
Harris C.M. (1998) On the optimal control of behaviour: a
stochastic perspective. Journal of Neuroscience
Methods 83: 73-88.
Harris C.M. (2004) Exploring smoothness and
discontinuities in human motor behaviour with Fourier
analysis. Mathematical Biosciences 188: 99-116.
Harris, C.M., 2002. Temporal uncertainty in reading the
neural code (proportional noise). Biosystems 67, 85-94.
Harris C.M., Harwood M.R. (2005) Boundary conditions
in human movement III: Fourier analysis of reaching.
In Proceedings of the IASTED International
Conference Biomedical Engineering, ACTA Press
Anaheim USA, 629-640.
Harris C.M. & Wolpert D.M. (1998) Signal-dependent
noise determines motor planning Nature 394, 780-784.
Harris C.M. & Wolpert D.M. (2006) The main sequence
of saccades optimizes speed-accuracy trade-off
Biological Cybernetics 95, 21-29.
Harwood M, Mezey, L, Harris CM. (1999) The spectral
main sequence of human saccades. Journal of
Neuroscience 19: 9098-9106.
Jones, K.E., Hamilton. A.F., Wolpert D.M. (2001) Sources
of signal-dependent noise during isometric force
production. Journal of Neurophysiology 88, 1533-1544.
Schmidt R.A., Zelaznik H., Hawkins B., Franks J.S.,
Quinn J.T.J. (1979) Motor output variability: a theory
for the accuracy of rapid motor acts. Psychological
Review 86, 415–451.
Simmons G. & Demiris Y. (2005) Optimal robot arm
control using the minimum variance model. Journal of
Robotic Systems 22: 677-690
BIOMIMETICS AND PROPORTIONAL NOISE IN MOTOR CONTROL
43
