DSP IMPLEMENTATION AND PERFORMANCES EVALUATION

OF JPEG2000 WAVELET FILTERS

Ihsen Ben Hnia Gazzah, Chokri Souani and

Kamel Besbes

Laboratoire Microélectronique et Instrumentation

Faculté des sciences de Monastir

Keywords: Discrete wavelet transform, lifting scheme, filter banks, DSP.

Abstract: The lifting scheme wavelet Transform allows efficiency implementation improvement over filter banks

model. In this paper, we present simulation results and DSP implementation results of Lifting scheme

algorithm for 1D and 2D discrete wavelet transform (2D-DWT). The lossless and lossy wavelet filters 5/3

and 9/7, respectively, have been used to transform images. The transforms have been implemented in a

float-point DSP chip and performances are evaluated. The DSP code was optimized at source code level and

memory usage. The implemented code is optimized in different ways especially within memory usage.

1 INTRODUCTION

Since their introduction by Wim Sweldens in 1994

(Sweldens, 1996), the discrete lifting scheme (LS)

wavelet transform has gained widely acceptance due

to their ability to construct biorthogonal wavelets in

the spatial domain independently of the Fourier

transform (Daubechies et al., 1998; Chendonga et al.,

2007; Delouille et al., 2006). The lifting scheme

was adopted as the base of the JPEG 2000 standard

(Rabbani et al., 2002). The image compression in

the JPEG2000 standard is performed either by the

9/7 real values wavelet or by the 5/3 integer values

wavelet.

The DWT has been implemented conventionally

using the filter bank scheme (FBS). This solution

implements filters with convolution technique. It

requires both a large number of clock cycles and a

large amount of storage memory. However, the

lifting scheme requires less computations and less

storage memory space. Recent studies tempted to

compare between LS and FBS. In this context,

Gnavi (Gnavi et al., 2002) implemented both DWT

methods and compared their performances for image

coding task. He has found that the LS

implementation run faster than the filter bank

scheme. Special-purpose hardware is used to reduce

the execution time of the DWT, Programmable

processors, however, are preferable because they are

more flexible. Furthermore, multimedia SIMD

extensions (Shahbahrami et al., 2005) can be used to

reduce the execution time of the DWT.

In this paper, we present simulation results of

Lifting scheme algorithm using Matlab tool, and

implementation results using a TMS320C6713 DSP

processor. The code is optimized in order to reduce

the execution time while performing the

reconstruction quality. The lossless 5/3 and the lossy

9/7 lifting scheme transform were considered. The

paper presents our contribution on the 2D-DWT-LS

implementation into DSP processor. The paper is

organized as follows: In section 2, a background of

the lifting scheme is briefly explained, while an

overview of our experimental results is given in

section 3. Conclusions and future work are drawn in

the end.

2 LIFTING SCHEME

ALGORITHM

Lifting scheme decomposition consists on splitting

the original signal into two subsets defined by the

even and odd index signal samples, and then

gradually a new wavelet coefficients set is built

(Sweldens et al., 1996) (figure 1). The

decomposition is held in three steps:

• Split: This step is called “Lazy wavelet

Transform (LWT)”. It consists on decomposing the

410

Ben Hnia Gazzah I., Souani C. and Besbes K. (2008).

DSP IMPLEMENTATION AND PERFORMANCES EVALUATION OF JPEG2000 WAVELET FILTERS.

In Proceedings of the First International Conference on Bio-inspired Systems and Signal Processing, pages 410-415

DOI: 10.5220/0001067004100415

 SciTePress

original image S into two sub-images. The two sub-

images are defined by the even (Se

) and the odd

(So

2i+1

) pixel image coefficients. The LWT is a

simple function switching coefficients

corresponding to their order (odd or even).

 Primal Lifting step: the original signal has

even and odd index samples interspersed. If the

signal has a local correlation structure, the even and

odd samples will be highly correlated. In other

words given one of the two sets, it should be

possible to predict the other set with reasonable

accuracy. The even set is always used to predict theo

dd one which represents the wavelet coefficients

(Daubechies et al., 1998).

are the wavelet

coefficients.

are the odd samples.

is the

prediction polynom and

are even samples (eq. 1)

()

ii i

So P Se=−

(1)

 Dual Lifting step: The update operator U is

applied to the wavelet coefficients computed

and then are addition with

to compute

(eq.

2).

are the scaling coefficients.

()

ii i

Se U H=+

(2)

3 EXPERIMENTATIONS AND

RESULTS

In this section, we describe first the implementation

of the DWT using lifting scheme into a DSP

processor.

Figure 1: Basic structure of one dimensional Discrete

Wavelet transform (1D-DWT) using lifting scheme (Ben

Hnia Gazzah et al., 2007).

3.1 Implementation

The 5/3 filter allows achieving lossless image

compression and has short filter taps composed of

3/2 coefficients respectively to the 5 and 3 filter taps.

The 9/7 filter is composed of 5/4 taps respectively.

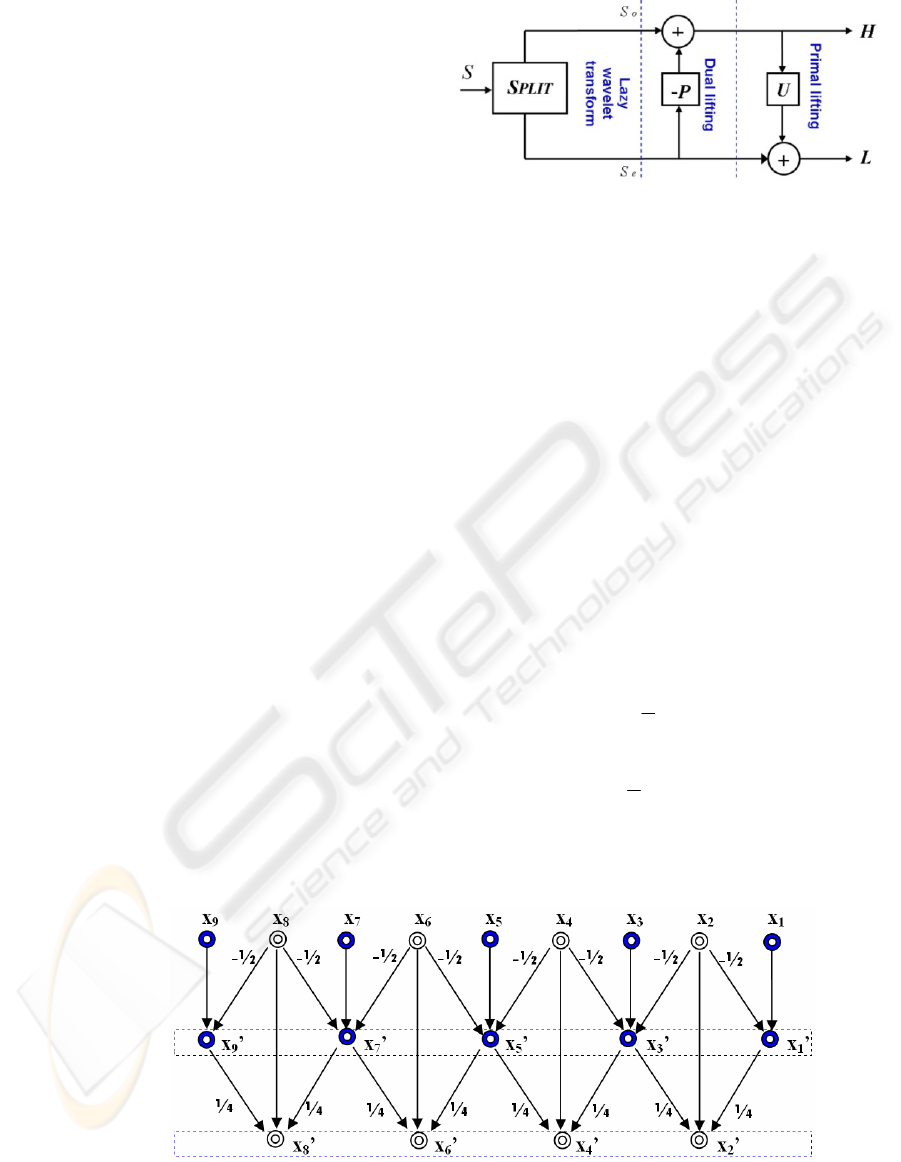
Figure2 shows the lifting scheme steps of the 5/3

wavelet filter. The Input samples

21k

and

denote the odd and even samples, respectively,

resulting from the split step provided by the Lazy

Wavelet Transform (LWT). The prediction and

updating steps are given by

21k

′

and

′

Coefficients

21k

′

and

′

are the output

coefficients obtained by the prediction task and the

updating task respectively.

21 21 2 22

()

kk kk

xx xx

++ +

=− +

(3)

'''

22 2121

()

kk k k

xx x x

−+

=+ +

(4)

Figure 2: The lifting scheme set for 5/3 filter (Ben Hnia Gazzah et al., 2007).

Low-pass output

High-pass output

Input sample

Prediction

Update

DSP IMPLEMENTATION AND PERFORMANCES EVALUATION OF JPEG2000 WAVELET FILTERS

411

The 9/7 decomposition is computed within fou

steps (Daubechies et al., 1998) as shown

equation 5-8:

21 21 2 22

*( )

kk kk

xxaxx

++ +

=+ +

(5)

'''

22 2121

*( )

kk k k

xxbx x

−

=+ +

(6)

21 21 2 22

*( )

kk kk

xxcxx

++ +

′′ ′ ′ ′

=+ +

(7)

22 2121

*( )

kk k k

xxdx x

−

′′ ′ ′′ ′′

=+ +

(8)

The lifting coefficients (Jiang et al., 2005) are: a=-

1.5861, b=-0.0529, c=0.8829 and d=0.4435. The

high-pass coefficients

21k

′′

, are normalized by a

weight K

=1.2302, and the low pass coefficients

′′

are normalized by K

=1/ K

The implementation is held with the Texas

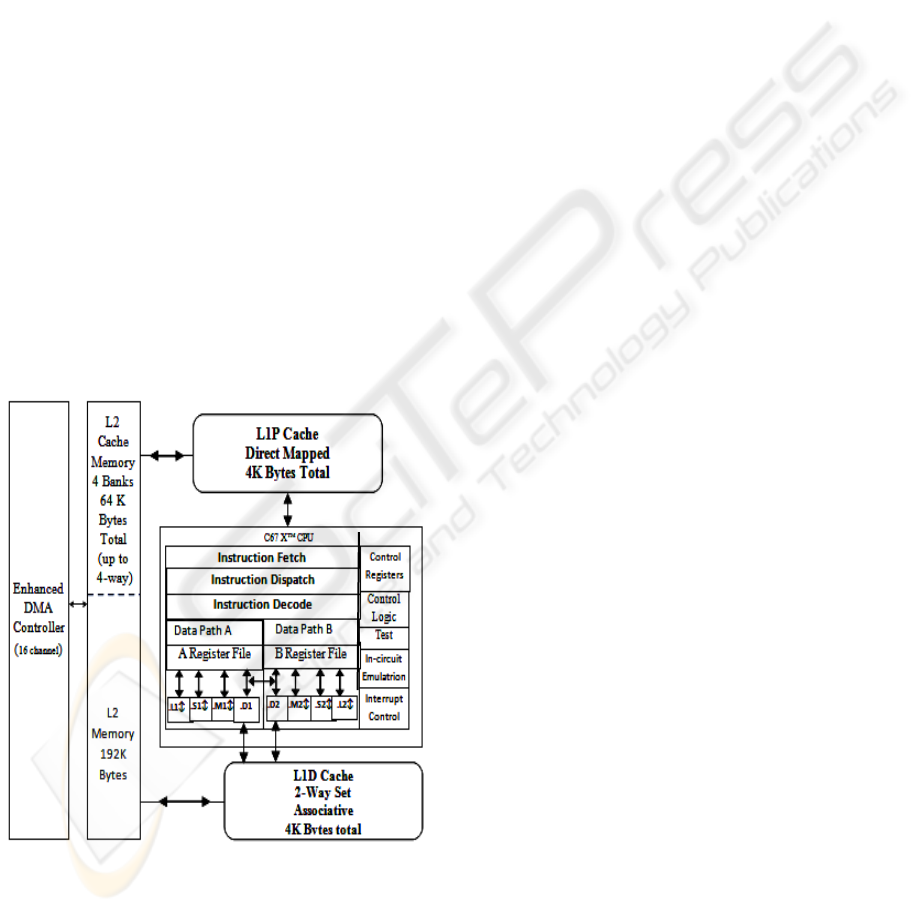
Instrument TMS320C6713 floating-point processor.

The TMS320C6713 processor is a fast special-

purpose microprocessor with adequate architecture

(figure 3) for signal processing (Texas Instrument,

2002).

Figure 3: Functional bloc of TMS320C6713 and CPU

diagram (Texas Instrument, 2002).

The TMS320C6713 is based on the VLIW

architecture and its performance is rated at 1800

MIPS. The internal program memory is structured so

that a total of eight instructions can be fetched every

cycle. With a clock rate of 255 MHz the processor is

capable of fetching eight 32-bit instructions every

4.44ns (Texas Instrument, 2001).

It is used only one storage memory block, in the

algorithm description. In both prediction and update

stages a new computed coefficient replaces the

original input value without need to additional

emplacements (in place calculus). The inverse

transform is easily performed by inversing the steps

of LS and the operations signs.

3.2 Experimental Results

The implementation performances are evaluated in

term of execution time and cycle’s number per

computed pixel. Performance was measured using

the cycle counters (Texas Instrument, 2002). Cycle

counters provide a very precise tool for measuring

the time that elapses between two different points in

the execution of a program.

Obviously the execution

time depends on the image size (table1), the type of

used memory (internal or external memory) and the

number of steps of lifting scheme. The running time

when using processor internal memory is shorter

than that when using external memory. In our case,

due to the limited size of the internal memory (256

KB), we are conducted to use the external memory

(16 MB SDRAM) as a “buffer memory”.

Table1 shows the execution time ratio of external

memory to internal memory. The mean value ratio

for 5/3 filter is about “21”, however, the mean value

is about “39” for the 9/7 filter. The mean value for

9/7 filter is two times higher then that for the 5/3

filter: this is due to the number of lifting scheme

steps. The transforms with less lifting steps 5/3 tend

to perform better than transforms with more lifting

steps 9/7 in term of speed. In addition, we have

implemented the 5/3 lifting scheme using only

addition, subtraction, and shifting operations without

multiplications.

The code optimization by using internal memory

reduces the execution time. Obviously the internal

memory access time is lower than that of external

memory.

Figure 4 shows the running time using internal

memory and figure 5 shows the running time using

external memory.

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

412

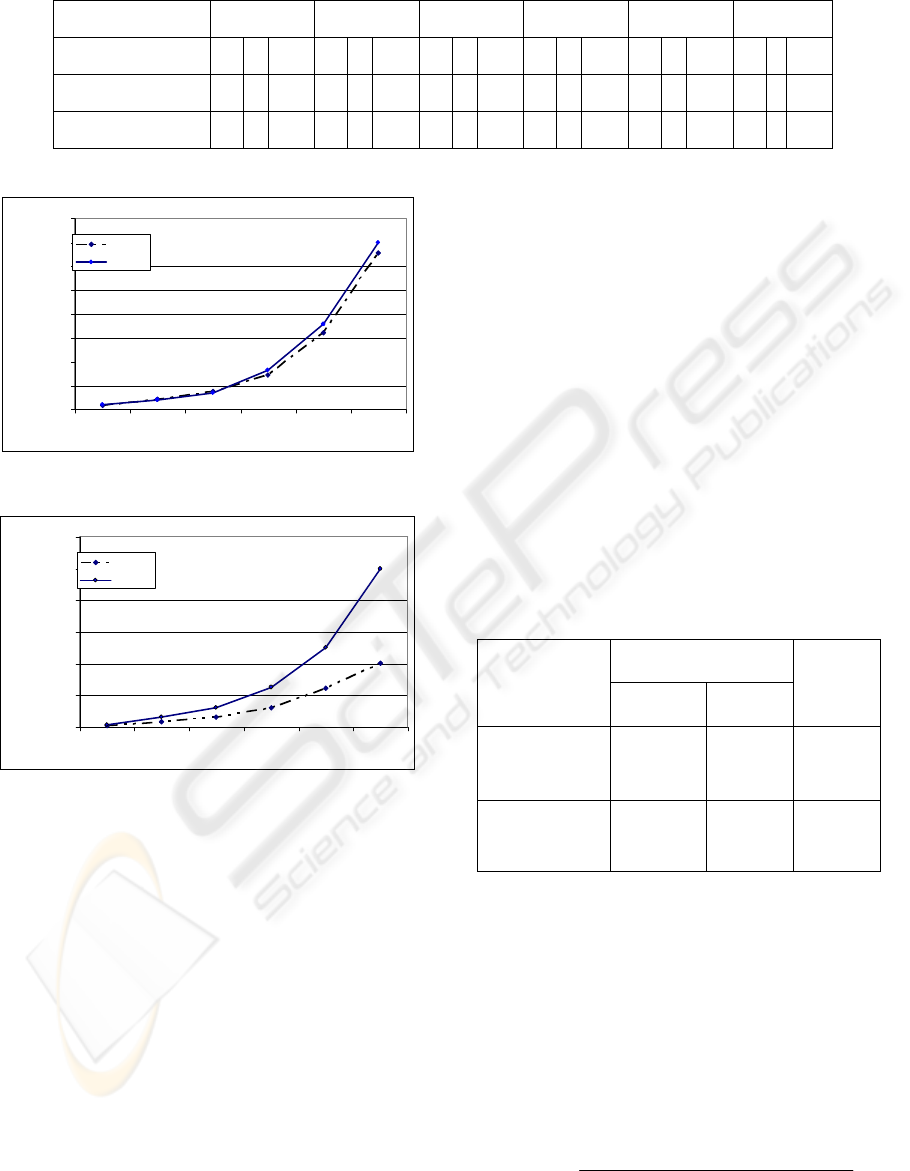
Table 1: Cycle’s number per pixel.

Samples number

64 256 512 1024 2048 4096

Memory type*

ext int Ratio ext int Ratio ext int Ratio ext int Ratio ext int Ratio ext in Ratio

5/3 filter

135 6 22.5 145 7 20.71 145 7 20.75 135 6 22.5 135 7 19.28 110 6 18.33

9/7 filter

274 7 39.14 273 7 39 274 7 39.14 275 7 39.28 275 7 39.28 275 7 39.29

*int = execution time of internal memory in cycles/pixel, ext = execution time of external memory in cycles/pixel

running time

100

120

140

160

64 256 512 1024 2048 4096

number of samples

time (microsecond

)

filter 5/3

filter 9/7

Figure 4: Running time using internal memory.

running time

1000

2000

3000

4000

5000

6000

64 256 512 1024 2048 4096

number of samples

time (microsecond

)

filter 5/3

filter 9/7

Figure 5: Running time using external memory (SDRAM).

Two sets of experiments of 1D- Discrete

Wavelet lifting implementation were performed: in

the first set, we used on-chip memory and external

memory. In the second set, we used only external

memory . Two programs have been implemented.

They differ in the processing part. In the first

program, the processing took place in the internal

memory (on-chip memory), however in the second

program, the processing part of the C-program is

held in the external memory.

Execution time results (cycles/pixel) for both

methods of the 1D- Discrete Wavelet lifting are

shown in Table 2. The comparison of the execution

time between both methods shows that the one using

internal memory is about three times faster than the

other using external memory SDRAM 16MB for the

filtering operation.

We optimize the execution time of the lifting

scheme by using internal memory for processing in

three steps:

First, the image is divided into several blocks

before storage into the SDRAM memory. Secondly,

the blocs are transferred in the L2 cache internal

memory. The filtering operation is performed by the

lifting scheme algorithm. Finally the transformed

image is transferred to the external memory

(SDRAM) for result storage.

Similarly, the next blocks of image are transferred

one after another into L2 cache where they are

processed. The number of blocks depends on the

image size. In the case of 256x256 image size, the

size of each block is 64x256 pixels. Four successive

blocks are to be used.

Table 2: Execution time of the 1D- Discrete Wavelet

lifting for image (Baboon 256x256) using 5/3 filter.

Execution time

(Cycles/pixel)

Execution

time A*

Execution

time B**

Ratio of B

to A

image(256*256

pixels)

decomposition

43 135 3.14

image (256*256

pixels)

reconstruction

43 134 3.16

*A : execution time using internal memory for processing.

**B : execution time using external memory for processing

(SDRAM).

The reconstructed image was compared to the

original image and the peak signal-to-noise ratio

(PSNR) in decibels was computed for images to

evaluate the performance of the wavelet lifting

scheme transform program. In the case of an image

whose intensity of the pixels lies between 0 and 255,

the PSNR is given by the following formula:

[]

255

10.log ( )

1/( . ) . ( ( , ) ( , ))

SNR dB

MN xi j xi j

−

∑∑

DSP IMPLEMENTATION AND PERFORMANCES EVALUATION OF JPEG2000 WAVELET FILTERS

413

where: M×N is image size computed in pixels

: (1<i<M) and (1<j<N) denote pixel indices.

We have founded a higher PSNR for wavelet

lifting scheme transforms. This verifies a perfect

reconstruction property of Wavelet lifting scheme

transform. Table3 shows the PSNR and SNR results

obtained by DSP implementation and MATLAB

simulation using 2D wavelet lifting scheme

transform for both 5, 3 and 9, 7 filters.

The 2-D discrete wavelet transform (DWT)

based on a lifting scheme, is carried out as a

separable transform by cascading two 1-D

transforms in the horizontal and vertical direction.

Each level of wavelet decomposition provides four

sub-bands of decomposition images: LL, LH, HL

and HH with halved resolution in both horizontal

and vertical directions.

In our application we implemented the 2D-DWT

on DSP using Lifting scheme until level three with

different image sizes: Barbara (512x512),

Cameraman (256x256), Lena (256x256), Baboon

(512x512), goldhill (512x512), lena(512x512).

The same algorithm was simulated using

Matlab language. We compared PSNR results of 2D

lifting scheme at level three using different image

sizes (table .3). Experimental and simulation results

have almost the same performance.

The following figure represents three levels of the

2D-DWT with Lifting implemented on DSP using

Barbara image (512 x 512 pixels).

Figure 6: 3-level 2D-DWT using lifting scheme with

Barbara image 512x512 pixels.

Table 3: PSNR results of 2D lifting scheme

implementation and MATLAB simulation (level three).

Wavelet CDF9/7 Wavelet LeGaull 5/3

image

Perfor-

mance Simulation

results

Experiment

results

Experimental

results

Simulation

results

PSNR (dB)

307.929 ∞ ∞ ∞

Barbara

512*512

SNR

301.522 ∞ ∞ ∞

PSNR (dB)

307.016 ∞ ∞ ∞

Baboon

512*512

SNR

301.550 ∞ ∞ ∞

PSNR (dB)

307.171 ∞ ∞ ∞

lena

512*512

SNR

301.514 ∞ ∞ ∞

PSNR (dB)

307.452 ∞ ∞ ∞

lena

256*256

SNR

301.647 ∞ ∞ ∞

PSNR (dB)

307.114 ∞ ∞ ∞

Camera-

man

256*256

SNR

301.532 ∞ ∞ ∞

PSNR(dB)

307.979 ∞ ∞ ∞

Goldhill

512*512

SNR

301.613 ∞ ∞ ∞

4 CONCLUSIONS AND FUTURE

WORK

In this paper, we reported the implementation of 2D-

DWT using lifting scheme algorithm on the

TMS320C6713 DSP, floating-point processor. We

used 5/3 and 9/7 filters. We compared the

implementation of the algorithm on DSP with the

simulation using Matlab.

For both methods, we obtained high PSNR

values of different images sizes confirming efficacy

of the approach. The most important advantages of

the lifting scheme (Ben Hnia Gazzah et al., 2007)

for wavelet transform were verified which are:

perfect reconstruction capability, in place

computation.

We optimized speed execution time of DSP

implementation of lifting scheme algorithm in

different ways especially within memory usage.

Execution times of the two algorithms of 5/3 and

9/7 filters on a DSP have been compared. The

corresponding C-program for a 1-level 1D DWT of

5/3 filter is up to 3x faster than of the 9/7. Integer to-

integer transforms are often faster than real-to-real

transforms, because the 5/3 wavelet filter requires

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

414

two lifting scheme steps, however the 9/7 wavelet

filter requires four ones.

The future work will be optimizing speed

execution time of lifting scheme algorithm using

DMA.

REFERENCES

Ben Hnia Gazzah, I., Souani, C., and Besbes, K., 2007,

“DSP implementation of lifting Scheme transform”,

Journées scientifiques des jeunes chercheurs en Génie

Electrique et Informatique, pp 445-451.

Chendonga, D., Zhengjiab, H., and Hongkai, J., 2007, A

sliding window feature extraction method for rotating

machinery based on the lifting scheme, Journal of

Sound and Vibration, vol. 299, pp 774–785.

Daubechies, I., and Sweldens, W., 1998, “Factoring

wavelet transforms into lifting steps,” Journal of

Fourier Analysis and Applications, vol. 4, pp. 245–

267.

Delouille, V., Jansen, M., and Von Sachs, R., 2006,

Second-generation wavelet denoising methods for

irregularly spaced data in two dimensions, Signal

Processing, vol. 86, pp 1435–1450.

Gnavi, S., Penna, B., Grangetto, M., Magli, E., and Olmo,

G., 2002, Wavelet Kernels on a DSP: A Comparison

Between Lifting and Filter Banks for image Coding,

EURASIP Journal on Applied Signal Processing,

Hindawi Publishing Corporation: 9, 981–989.

Jiang, K., Dubois, E., 2005, Lifted wavelet-based image

dataset compression with column random access for

image-based virtual environment navigation, IEEE

International Workshop on Haptic Audio Visual

Environments and their Applications, Ottawa, Ontario,

Canada.

Rabbani, M., and Josi, R., 2002, An Overviewof the the

JPEG2000 Still Image Compression Standard Signal

Processing: Image Communication, 17(1), pp.3-48.

Shahbahrami, A., Juurlink, B., and Vassiliadis, S., 2005

Performance Comparison of SIMD Implementations

of the Discrete Wavelet Transform, Proc. 16th IEEE

Int. Conf. on Application-Specific Systems

Architectures and Processors (ASAP), Samos, Greece,

July 23-25.

Sweldens, W., 1996, Wavelets and the lifting scheme, A 5

minute tour, Zeitschrift für Angewandte Mathematik

und Mechanik, vol. 76 (Suppl. 2), pp. 41-44.

Sweldens, W., and Schröder, 1996, Building your own

wavelets at home, in Wavelets in Computer Graphics,

ACM SIGGRAPH course notes, pp. 15-87.

Texas Instrument, Revised November 2002,

TMS320C6713 Floating-Point Digital Signal

Processor, Datasheet SPRS186B

Texas Instrument, december 2001, TMS320C6713

Floating-Point Digital Signal Processor, Datasheet

SPRS186L.

DSP IMPLEMENTATION AND PERFORMANCES EVALUATION OF JPEG2000 WAVELET FILTERS

415