
A STUDY ON ILLUMINATION NORMALIZATION
FOR 2D FACE VERIFICATION
Qian Tao and Raymond Veldhuis
Signals and Systems Group, Universiteit Twente, Postbus 217, Enschede, The Netherlands
Keywords:
Illumination normalization, face recognition, local binary patterns, Gaussian derivative filters.
Abstract:
Illumination normalization is very important for 2D face verification. This study examines the state-of-art
illumination normalization methods, and proposes two solutions, namely horizontal Gaussian derivative filters
and local binary patterns. Experiments show that our methods significantly improve the generalization capabil-
ity, while maintaining good discrimination capability of a face verification system. The proposed illumination
normalization methods have low requirements on image acquisition, and low computation complexities, and
are very suitable for low-end 2D face verification systems.
1 INTRODUCTION
The 2D face image, as an important biometric, has
been a popular research topic for decades. With the
development of low-cost electronic devices, 2D face
images can be easily obtained through digital cam-
eras, webcams, mobile phones, etc. This makes it
possible to use 2D face images as an easy and inex-
pensive biometric for security purposes. For example,
2D face images can be used for user verification of a
mobile device (and hence the network connected to
this device), or a computer system containing private
user information.
The variability on the 2D face images brought by
illumination changes is one of the biggest obstacles
for reliable and robust face verification. Research
has shown that the variability caused by illumination
changes can easily exceeds the variability caused by
identity changes (Moses et al., 1994). Illumination
normalization, therefore, is a very important topic to
study.
This paper is organized as follows. Section 2
briefly reviews the current illumination normalization
methods, including 3D and 2D approaches. Section 3
proposes two simple and efficient solutions, namely
horizontal Gaussian derivative filters and Local Bi-
nary Patterns. Section 4 introduces the likelihood ra-
tio based face verification, and presents an analysis of
the illumination normalization methods under the ver-
ification framework. Section 5 describes the results of
our solutions on laboratory data and Yale database B
(Georghiades et al., 2001). Section 6 draws conclu-
sions.
2 A REVIEW ON ILLUMINATION
NORMALIZATION METHODS
2.1 3D Illumination Normalization
Methods
Illumination on faces is essentially a 3D problem.
Proposed 3D illumination normalization methods aim
to solve the problem on 2D images from the 3D
point of view. Examples are the illumination cone
(Belhumeur and Kriegman, 1998), quotient image
(Shashua and Riklin-Raviv, 2001), shape from shad-
ing (Sim and Kanade, 2001), etc. All the methods
have the same basic physical model, assuming Lam-
bertian reflectance
I(x,y) = ρ(x, y)~n(x,y)
T
~
s (1)
where (x,y) are the coordinates on the face im-
age, I(x,y) is the corresponding image pixel values,
ρ(x,y) ∈ R is the albedo at this point, ~n(x, y) ∈ R
3
is
the face surface normal, and
~
s ∈ R
3
is the light source,
representing both the direction and intensity. By pro-
jection the problem back to the 3D domain, it is as-
sumed that the effects of
~
s can be decoupled by re-
covering ρ or n in either an explicit or inexplicit way.
42
Tao Q. and Veldhuis R. (2008).
A STUDY ON ILLUMINATION NORMALIZATION FOR 2D FACE VERIFICATION.
In Proceedings of the Third Inter national Conference on Computer Vision Theory and Applications, pages 42-49
DOI: 10.5220/0001082900420049
Copyright
c
SciTePress

(a)
(b)
(c)
(a)
(b)
(c)
(a)
(c)
(b)
Figure 1: Examples of quotient images: left - good example when the shadow-free assumption and constant-shape assumption
are well satisfied, middle - example when strong shadow exists, right - example when the shape are not well aligned. In
all cases, (a) is the original image, (b) is the quotient image, (c) is the rerendering of the original image under different
illuminations, indicating the accuracy of the quotient image.
To recover the 3D information from the 2D im-
ages, assumptions are necessary to rebuild the lost in-
formation. Most illumination normalization methods
based on the Lambertian model have two underlying
assumptions: first, the face image is shadow-free (i.e.
~n(x, y)
T
~
s > 0), and second, the faces has constant 3D
shape~n, as rigid objects. In reality, these two assump-
tions are often not true. The shadow-free face im-
ages are only available under frontal or near-frontal
lighting conditions. For example, the nose very often
causes shadows when lighting is from the side. The
constant shape assumption is easily violated by slight
pose changes or expressions. In (Sim and Kanade,
2001), where the surface normals ~n are estimated in
a MAP (maximum a posteriori) manner without con-
stant shape assumptions, it is also found that the algo-
rithm can only achieve good performance under near-
frontal illuminations. Shadows give rise to loss of
information, which cannot be easily recovered. As
an example of 3D methods, Fig. 1 shows the quo-
tient images (Shashua and Riklin-Raviv, 2001) un-
der three situations, giving some feeling how shad-
ows and shape changes harm the performance of 3D
methods. It can be seen from the quotient image that
shadows cannot be reliably removed, and that the mis-
alignment of the face shape causes artifacts, which
can be more easily observed from the rerendered im-
age. Although the results are only shown for the quo-
tient image method, these drawbacks exist in general
for Lambertian model-based 3D illumination normal-
ization methods.
To summarize, 3D methods aim to recover the 3D
information, which is fundamental of a face, there-
fore, they can be expected to achieve very good per-
formance. However, as converting 3D objects to 2D
images is a process with loss of information, the re-
verse process will unavoidably have restrictions, such
as fixed shape, absence of shadow, training images
under strictly controlled illuminations. These restric-
tions limit the range of face verification applications,
especially when the acquired face image are of low-
resolution, low-quality, and with unconstrained illu-
minations.
2.2 2D Illumination Normalization
Methods
2D illumination normalization methods do not rely
on recovering 3D information, instead, they work di-
rectly on the 2D image pixel values. Examples are
the linear high-pass filter which models the illumi-
nation as an addictive effect, The Retinex approach
(Land and McCann, 1971) (Jobson et al., 1997) which
models the illumination as a multiplicative effect, the
diffusion approach (Perona and Malik, 1990) (Chan
et al., 2003) which relies on partial differential equa-
tions, and local binary patterns (LBP) (Ahonen et al.,
2004) (Heusch et al., 2006) which encode the image
value by binary thresholding.
A close examination of these methods reveals that
most of the 2D illumination normalization methods
are essentially linear or nonlinear high-pass filters,
emphasizing edges in image. This can be easily un-
derstood, because illumination changes often appear
as low-pass effects on an image, while the facial fea-
ture edges are intrinsically high-frequency. Modu-
lated by the 3D shape and surface albedo, however,
the illumination cannot be simply seen a the low fre-
quency component of the image. Taking Fig. 1 as
an example, illumination also causes high frequency
edges on 2D face image, most frequently around the
nose area, and also unpredictably in other places. The
edges caused by illumination can be very strong. The
biggest problem for 2D illumination normalization
A STUDY ON ILLUMINATION NORMALIZATION FOR 2D FACE VERIFICATION
43

filterbank
Figure 2: Original image, filterbank (including Gabor filters, Gaussian and Laplacian fitlers, first and second order Gaussian
derivative filters), and filtered images.
methods, therefore, is that the high frequency edges
caused by illumination cannot be easily discriminated
from the edges belonging to the face. If local meth-
ods are used, all the edges are deemed equivalent; if
global methods are used, a model must be built up to
discriminate the two types of edges, but introducing a
model itself has the risk of bringing errors if it cannot
be fitted well, as in the case of 3D methods.
2.3 Summary
Invariance to illumination is very desirable but cannot
be easily achieved. For 3D methods it is in theory pos-
sible, by recovering the lost information through ex-
tensive training on illuminations, poses, and expres-
sions, but the cost is very high. For 2D methods it is
theoretically not possible, as stated in (Chen et al.,
2000): for an object with Lambertian reflectance
there are no discriminative functions that are invari-
ant to illumination.
In this work, we aim for simple and efficient 2D
methods, which are insensitive to illumination. With-
out strict and rigid restrictions, 2D methods put lower
requirements on image acquisition process and hard-
ware devices. We propose two 2D methods, and show
how insensitivity is achieved. Furthermore, we show
under a verification framework, how our methods are
related to the generalization capability and discrimi-
nation capability of the classifier.
3 ILLUMINATION-INSENSITIVE
FILTERS
3.1 Horizontal Gaussian Derivative
Filters
Gabor, Gaussian, Laplacian, and Gaussian derivative
filters are popular 2D filters widely used in image pro-
cessing and computer vision (Varma and Zisserman,
2005). Each of them can emphasize certain type of
image textures, and has different sensitivity to noise
or illumination. In Fig. 2, we show a bank of these
filters with different scales, orientations, and aspect
ratios. The face image and the filtered image are also
shown.
As can be observed from Fig. 2, the Gabor fil-
ters emphasize textures of certain orientation, scale,
and frequency; Gaussian and Laplacian filters are not
directional, but are selective on the sizes of dots or cir-
cles; the first and second order Gaussian derivative fil-
ters concentrate on edges of different sizes and direc-
tions. As in the original image the illumination cre-
ates edges mostly in vertical directions, it can be seen
that the illumination effects are less obvious in im-
ages filtered by the horizontal directional filters. For
example, in the filtered image on the lower left corner,
almost no indication of side lighting can be observed.
Interestingly enough, most of the important face
textures, like eyebrows, eyes, mouth, except nose, are
more in horizontal directions than in vertical direc-
tions. The nose is informative in the 3D sense, but
in the 2D images, it is often sensitive to illuminations
due to its nonuniform surface normals. Moreover, the
nose often causes shadows along its center line. Gen-
erally speaking, the edges caused by illumination are
more often in vertical directions than horizontal. This
has inspired us to use the horizontal filters to make
the image insensitive to illumination. We select the
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
44

(a) Images from the Yale database, same subject
(b) Real life images, different subjects
Figure 3: (For difficult illumination changes) Examples of
face images under different illumination and the filtered im-
ages. The filtered images are more insensitive to illumina-
tions.
(a) (b) (c) (d)
Figure 4: Four simple illumination patterns, (a) uniform in-
tensity, (b)(c)(d) linearly increasing intensity, direction indi-
cated by the arrowhead. The convolution result of the filter
with these four simple illumination patterns are zero.
second order Gaussian derivative filter, as marked by
the rectangle in Fig. 2.
We further show more examples indicating the in-
sensitivity of this filter in Fig. 3. The size of the
filter is tuned so that it can extract important facial
texture information, but meanwhile filter out vertical
edges and small-size noises. Besides, this filter has
the good properties that all the columns are symmet-
ric and sum up to zero, which make it invariant to
the following four types of simple illumination pat-
terns, as shown in Fig. 4. In other words, if in certain
imaging model, these illumination patterns are addic-
tive, the linear property of 2D linear filters can guar-
antee invariance to these patterns. More generally
speaking, the null space of the horizontal Gaussian
second order derivative filter
∂
2
G(x,y)
∂y
2
(where G(x, y)
is the two dimensional Gaussian filter) can be given:
P(x,y) = f (x)+y + c, where P(x,y) denotes the pixel
values at point (x, y) and f (x) is any function of x, as
it follows that
∂
2
G(x,y)∗P(x,y)
∂y
2
= 0.
3.2 Local Binary Patterns as a Filter
Besides the image textures, the image intensities are
also very sensitive to illuminations. Difficult illumi-
nation changes alter the image texture, while ordinary
5 9 1
4 4 6
7 2 3
1 1 0
1
*
1
1 0 0
Binary: 11010011
Decimal: 211 (256-pattern)
Simplified: 5 (9-pattern)
threshold
Figure 5: The LBP operator: the binary result, decimal re-
sult, and the simplified LBP result.
Figure 6: (For ordinary illumination changes) The effects
of LBP preprocessing: first column - the original images
under different illumination intensities; second column - the
original LBP preprocessing; third column - the simplified
LBP preprocessing. The face size is 64 by 64.
illumination changes mostly alter the image intensi-
ties. This can be clearly seen from (1), in which the
three elements of
~
s can be any value. A linear filter
in principal cannot solve this problem. In order to
achieve insensitivity to intensities, we propose to use
the local binary patterns (LBP) as a nonlinear filter on
the image values.
Local binary patterns were proposed in (Ojala
et al., 2004), and have proved to be useful in a va-
riety of texture recognition tasks. The basic idea is
illustrated in Fig. 5: each 3 × 3 neighborhood block
in the image is thresholded by the value of its center
pixel. The eight thresholding results form a binary
sequence, representing the pattern at the center point.
A decimal representation is obtained by taking the bi-
nary sequence as a decimal number between 0 and
255.
The advantage of LBP is twofold. Firstly it is a lo-
cal measure, so the LBPs in a small region are not af-
fected by the illumination conditions in other regions.
Secondly it is a relative measure, and is therefore in-
variant to any monotonic transformation such as shift-
ing, scaling, or logarithm of the pixel-values. For a
pixel, LBP only accounts for its relative relationship
with its neighbours, while discarding the information
of amplitude.
In the initial work of face recognition using LBP
(Ahonen et al., 2004), a histogram of the LBPs is cal-
culated, representing the distribution of 256 patterns
across the face image. The distribution of LBPs can
be used as a good representation for images with more
or less uniform textures, but for the face images it is
not enough. A distribution loses connection between
A STUDY ON ILLUMINATION NORMALIZATION FOR 2D FACE VERIFICATION
45

the patterns and their relative positions in face. To
take advantage of both the local patterns and the po-
sitional information, LBP can be instead used as pre-
processing, or filter, on the image values.
Essentially LBP preprocessing acts as a nonlinear
high-pass filter on the image values. It emphasizes
the edges, as well as the noise. Because noise occurs
randomly in direction, the exponential weights on the
neighbors subject the LBP values to large variabili-
ties. To make the patterns more robust, we propose
simplification on the original LBP, assigning equal
weights to each of the 8 bits. The result simply adds
up all the 1’s, as shown in Fig. 5. In total the sim-
plified LBP only has 9 possible values. Fig. 6 shows
the filtering effects of the original LBP and simplified
LBP on two images with different illumination inten-
sities.
It might be argued that LBP as a filter throws away
amplitude information and therefore will harm the
face verification performance. The simplified LBP
merges many different LBP patterns into one, giving
rise to even more loss of information. Experimental
results, however, will show that LBP preprocessing
significantly increases the generalization capability of
the verification system, at virtually no expense of dis-
crimination capability. This will be further discussed
in the next section under the verification framework.
4 FACE VERIFICATION
4.1 Likelihood Ratio Based Face
Verification
Verification is a very important application in biomet-
rics. It checks the legitimacy of the claimed user, pre-
venting the impostors from abusing the user’s system,
or accessing important user information. The out-
put of verification is either 1 (user) or 0 (impostor).
Our face verification is based on the likelihood ratio,
which is defined by
L(x) =
p
user
(x)
p
bg
(x)
(2)
where p
user
is the user data distribution, and p
bg
is
the background distribution (including all the possible
data). Fig. 7 illustrates the relationship between these
two distributions. If the likelihood ratio L is larger
than a certain value T , a decision of 1 is made, other-
wise a decision of 0 is made. The likelihood ratio cri-
terion is optimal in the statistical sense, and it easier
to apply than the Bayesian method. In the Bayesian
method, the prior probabilities (or cost) of the user
p
user
p
bg
Figure 7: The distribution of the user data and the back-
ground data.
class and the background class have to be defined ex-
plicitly to determine T , while in the likelihood ratio
method, T can be more easily determined by some
performance criterion, like FAR (false accept rate)
or FRR (false reject rate). In an easy and effective
manner, the user class and the background class are
modeled by two multivariate Gaussian distributions,
learned from the training data. More mathematical
details can be found in (Veldhuis et al., 2004).
4.2 Illumination Normalization
Preprocessing under the Verification
Framework
For verification, the preprocessed face image is
stacked into a feature vector x. A small enough face
image, for example, with the size of 32 × 32, has
1,024 pixels, which implies 1,024 degrees of free-
dom for the feature vector. The verification of a face
image, therefore, will be in a very high-dimensional
space. High-dimensional space potentially has very
large power of discrimination (Tax, 2001). For a sim-
ple example, suppose each of the user and the back-
ground class take up a hyper-sphere with radius r
user
and r
bg
= α · r
user
(α > 1) in a N dimensional space,
then from a single dimension, the user space takes up
1
α
of the background space. However, from all the N
dimensions, this ratio become
1
α
N
. When N is large,
1
α
N
becomes infinitely small. This means for an arbi-
trary feature vector, the chance that it falls in the back-
ground class is a great deal larger than the chance that
it falls in the user class.
Generalization capability and discrimination ca-
pability are two equally important aspects in verifica-
tion. But in a high-dimensional space, the prospects
of the two aspects seem to be imbalanced. We take
advantage of this, making large reductions on the in-
formation (e.g. vertical textures and amplitude differ-
ence) which are sensitive to illumination. This acts
as a restriction on either space, but reduces the back-
ground space more substantially than the user space
(equivalently, α becomes smaller). As a result, good
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
46

generalization discriminationtraining data
Figure 8: Laboratory data: the training data and the two
types of test - generalization capability and discrimination
capability.
generalization across illumination is achieved, while
enough discrimination still remained because of the
high dimensionality.
5 EXPERIMENTS AND RESULTS
To validate proposed the illumination normalization
methods, we collected data under laboratory condi-
tions
1
. We collected 10 subjects, each in indepen-
dent sessions under 3 completely different illumina-
tions. The number of images per session is 1,200.
The experiments take into consideration two impor-
tant aspects of the face verification system: discrim-
ination which is closely related to the security of the
verification system, tested by different subjects un-
der the same illumination; generalization which is
closely related to the user-friendliness of the verifi-
cation system, tested by the same subject under dif-
ferent illumination. Fig. 8 illustrates the two types
of test. The user space is trained on one session of
the user data, while the background space is trained
on three public face databases, namely the BioID
database (BioID), FERET database (FERET), and
FRGC database (FRGC).
The receiver operation characteristic (ROC) is an
indication of the system performance. It can be ob-
tained by thresholding the matching scores (in our
work likelihood ratio L) of the user data and the im-
postor data. The selection of the final threshold de-
pends on the application requirement, e.g. false ac-
cept rate or false reject rate, by taking the thresh-
old corresponding to such a operation point on the
ROC. We adapt very harsh testing protocols: the user
matching scores are calculated as the likelihood ra-
tio L of the user data in all the independent sessions
with completely different illuminations, while the im-
postor matching scores are calculated as the likeli-
1
Most publicly available database do not contain enough
number of images per user to train a user-specific space.
Our larger database is still under construction, and the data
used in this paper are available on request.
hood ratio L of all the other 9 subjects under ex-
actly the same illuminations as the training data. We
test the illumination normalization methods in 6 dif-
ferent schemes: (1) shifting and rescaling every fea-
ture vector to zero mean and unit variance (NORM1)
(2) horizontal Gaussian derivative filter (HF), fol-
lowed by NORM1; (3) original LBP filtering (LBP-
256); (4) simplified LBP filtering (LBP-9); (5) hori-
zontal Gaussian derivative filter, followed by original
LBP filtering (HF+LBP-256); (6) horizontal Gaussian
derivative filter, followed by simplified LBP filtering
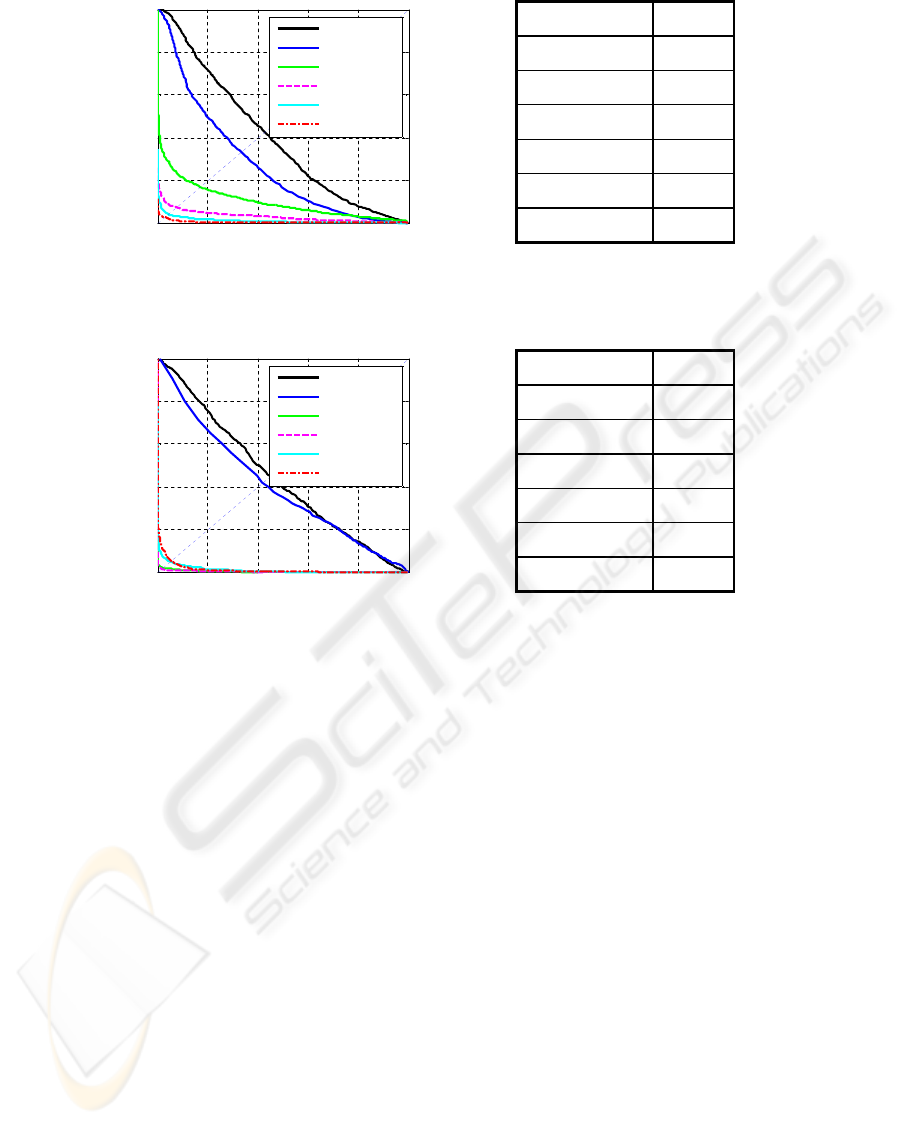
(HF+LBP-9). Fig. 9 (a) shows the ROCs of the 6 illu-
mination normalization methods, along with the equal
error rates (EER) of the verification. In all the tests, a
Gaussian horizonal filter with width σ
x
= 5, σ
y
= 1 is
applied to the face images of size 100× 100. The filter
extracts fine horizontal information while discarding
vertical information.
The experiments show that when only NORM1
is applied, the verification performance is poor, indi-
cating that different illuminations make large differ-
ences across face images of the same subject. The
same is true for horizontal Gaussian derivative filter
followed by NORM1, as illumination intensities also
make large differences on the feature vectors. The
two LBP filters have better verification performance,
while horizontal Gaussian derivative filter followed
by LBP filters (especially LBP-9) yields the best ro-
bustness to illumination. This experiment setting pro-
vided a way to validate and compare these illumina-
tion normalization methods. Although the harshness
of the test puts forward high requirements on the illu-
mination normalization methods, the results in Fig. 9
(a) do illustrate the potence of our solutions. Exper-
iments on larger databases are still being done for a
more comprehensive report.
The algorithm were also tested on the Yale
database B (Georghiades et al., 2001), which contains
the images of 10 subject, each seen under 576 view-
ing conditions (9 poses × 64 illuminations). For each
subject, the user data are randomly partitioned into
80% for training, and 20% for testing. The data of the
other 9 subjects are used as the impostor data. We also
test the six different illumination schemes, as shown
in Fig. 9 (b). In this experiment, it can be noticed that
horizontal Gaussian derivative filter does not further
improve the performance, which can be explained by
the fact that the Yale database B contains very ex-
treme illuminations, which cause deep shadows and
strong edges in horizontal directions. Our laboratory
data are more realistic.
A STUDY ON ILLUMINATION NORMALIZATION FOR 2D FACE VERIFICATION
47
Method EER
NORM1 42.60%
HF + NORM1 33.42%
LBP256 16.88%
LBP9 7.31%
HF + LBP256 4.16%
HF + LBP9 2.53%
0 0.2 0.4 0.6 0.8 1
0
0.2
0.4
0.6
0.8
1
FAR
ROC
FRR
NORM1
HF+NORM1
LBP256
LBP9
HF+LBP256
HF+LBP9
(a) laboratory data
0 0.2 0.4 0.6 0.8 1
0
0.2
0.4
0.6
0.8
1
FAR
FRR
ROC
NORM1
HF+NORM1
LBP256
LBP9
HF+LBP256
HF+LBP9
Method EER
NORM1 44.98%
HF + NORM1 41.80%
LBP256 1.99%
LBP9 1.52%
HF + LBP256 4.88%
HF + LBP9 5.32%
(b) Yale database B
Figure 9: ROCs and EERs of the 6 illumination normalization methods on laboratory data and Yale database B.
6 CONCLUSIONS
This paper presented a close study on illumination
normalization for 2D face verification. We reviewed
the state-of-arts illumination methods, and proposed
two simple and efficient solutions, namely horizon-
tal Gaussian derivative filters, and LBP filters. Pre-
liminary experiments show that the insensitivity of
face images to illuminations can be substantially in-
creased, when the proposed LBP filters or horizon-
tal Gaussian derivative filters followed by LBP filters
are applied. Taking advantage of the high dimension-
ality of face images, our methods improve the gen-
eralization capability of a face verification, at virtu-
ally no expense of discrimination capability. Both of
the two methods have low requirements on image ac-
quisition, and low computation complexities, and are
therefore very suitable for low-end 2D face verifica-
tion systems.
ACKNOWLEDGEMENTS
This work is funded by the Freeband PNP2008 project
of the Netherlands.
REFERENCES
Ahonen, T., Pietikinen, M., Hadid, A., and Menp, T. (2004).
Face recognition based on the appearance of local re-
gions. In IEEE International Conference on Pattern
Recognition.
Belhumeur, P. and Kriegman, D. (1998). What is the set
of images of an object under all possible illumina-
tion conditions. International Journal on Computer
Vision, 28(3):1–16.
Chan, T., Shen, J., and Vese, L. (2003). Variational pde
models in image processing. Notices of the American
Mathematical Society, 50(1):14–26.
Chen, H., Belhumeur, P., and Jacobs, D. (2000). In search of
illumination invariants. In IEEE Conference on Com-
puter Vision and Pattern Recognition, pages 254–261.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
48

Georghiades, A., Belhumeur, P., and Kriegman, D. (2001).
From few to many: Illumination cone models for face
recognition under variable lighting and pose. IEEE
Transactions on Pattern Analysis and Machine Intel-
ligence, 23(6):643–660.
Heusch, G., Rodriguez, Y., and Marcel, S. (2006). Local bi-
nary patterns as image preprocessing for face authen-
tication. In IEEE International Conference on Auto-
matic Face and Gesture Recognition.
Jobson, D., Rahmann, Z., and Woodell, G. (1997). Prop-
erties and performance of a center/surround retinex.
IEEE Transactions on Image Processing, 6(3):451–
462.
Land, E. and McCann, J. (1971). Lightness and retinex
theory. Journal of the Optical Society of America,
61(1):1–11.
Moses, Y., Adini, Y., and Ullman, S. (1994). Face recog-
nition: The problem of compensating for changes in
illumination direction. In European Conference on
Computer Vision.
Ojala, T., Pietikainen, M., and Maenpaa, T. (2004). Mul-
tiresolution gray-scale and rotation invariant texture
classification with local binary patterns. IEEE Trans-
actions on Pattern Analysis and Machine Intelligence,
24(7):971–987.
Perona, P. and Malik, J. (1990). Scale-space and edge de-
tection using anisotropic diffusion. IEEE Transac-
tions on Pattern Analysis and Machine Intelligence,
12(7):629–639.
Shashua, A. and Riklin-Raviv, T. (2001). The quotient im-
age: class based re-rendering and recognition with
varying illuminations. IEEE Transactions on Pattern
Analysis and Machine Intelligence, 23(2):129–139.
Sim, T. and Kanade, T. (2001). Illuminating the face. Tech-
nical report, Robotics Institute, Carnegie Mellon Uni-
versity.
Tax, D. (2001). One class classification. Ph.D. thesis, Delft
University of Technology.
BioID. Bioid face database. http://www.humanscan.de/.
FERET. Feret face database. http://www.itl.nist.
gov/iad/humanid/feret/.
FRGC. Frgc face database. http://face.nist.gov/
frgc/.
Varma, M. and Zisserman, A. (2005). A statistical approach
to texture classification from single images. Interna-
tional Journal on Computer Vision, 62(1-2):61–81.
Veldhuis, R., Bazen, A., Kauffman, J., and Hartel, P. (2004).
Biometric verification based on grip-pattern recogni-
tion. In Proceedings of SPIE.
A STUDY ON ILLUMINATION NORMALIZATION FOR 2D FACE VERIFICATION
49
