APPROXIMATE POINT-TO-SURFACE REGISTRATION WITH
A SINGLE CHARACTERISTIC POINT
Darko Dimitrov, Christian Knauer
∗
, Klaus Kriegel
∗
and Fabian Stehn
∗
Institut f¨ur Informatik, Freie Universit¨at Berlin, Berlin, Germany
Keywords:
Point-to-surface registration, matching, medical navigation, approximation algorithms.
Abstract:
We present approximation algorithms for point-to-surface registration problems which have applications in
medical navigation systems. One of the central tasks of such a system is to determine a “good” mapping (the
registration transformation or registration for short) of the coordinate system of the operation theatre onto the
coordinate system of a 3D model M of a patient, generated from CR- or MRT scans.
The registration ϕ is computed by matching a 3D point set P measured on the skin of the patient to the 3D
model M. It is chosen from a class R of admissible transformations (e.g., rigid motions) so that it approxi-
mately minimizes a suitable error function e (such as the directed Hausdorff or mean squared error distance)
between ϕ(P) and M, i.e., ϕ = argmin
ϕ
′
∈R
e(ϕ
′
(P),M). A common technique to support the registration pro-
cess is to determine either automatically or manually so-called characteristic points or landmarks, which are
corresponding points on the model and in the point set. Since corresponding characteristic points are supposed
to be mapped onto (or close to) each other, this reduces the number of degrees of freedom of the matching
problem.
We provide approximation algorithms which compute a rigid motion registration in the most difficult setting
of only a single characteristic point.
1 INTRODUCTION
Most neurosurgical and an increasing number of oto-
laryngological operations currently require the sup-
port of medical navigation systems. The purpose of
these systems is to provide an augmented image of
the patient, e.g., the correct projection of the used in-
strument into a 3D model of the area of interest, such
as the patient’s skull. To compute this projection, a
good transformationhas to be determined which maps
the coordinate system of the operation field to the co-
ordinate system of the model. Such transformations
are called registrations, and their approximation is the
central task we are investigating in this paper.
Several approaches are known to solve this problem.
Some of the methods currently used in practice are
based on fiducial landmarks. Such landmarks are ar-
tificial markers, e.g., plastic cylinders containing a
metal ball, which are attached to the skin of the pa-
tient and can automatically be detected in the model.
In the beginning of the surgery these marker positions
∗
Supported by the German Research Foundation (DFG),
grant KN 591/2-1.
are gauged with a traceable device. Then the registra-
tion is determined by mapping the measured points to
the landmarks in the model.
Other solutions are based on geodesics and local ge-
ometry as in (Wang et al., 2000). A feature-based ap-
proach using thin-plate splines is presented in (Chui
and Rangarajan, 2003) and applications in transcra-
nial magnetic stimulation by point-to-surface regis-
tration using ICP are discussed in (Matth¨aus et al.,
2006). These methods are either heuristics and there-
fore cannot provide guarantees on the quality of the
result or are very sensitive to lost, misplaced or dis-
placed landmarks.
In recent years algorithms havebeen developed which
solve this registration problem by using so-called
characteristic points, which are gauged along with
an arbitrary set of points from the skin of the pa-
tient. Characteristic points are unique points in the 3D
model with special anatomic properties, as the root of
the nasal bone and givehints for the correct placement
of the measured points.
The most general and difficult variant of rigid point-
to-surface registration with characteristic points is the
188
Dimitrov D., Knauer C., Kriegel K. and Stehn F. (2008).
APPROXIMATE POINT-TO-SURFACE REGISTRATION WITH A SINGLE CHARACTERISTIC POINT.
In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 188-195
DOI: 10.5220/0001085601880195
Copyright
c
 SciTePress

scenario where only a single characteristic point can
be measured in the operation field. These scenarios
occur for example when the target area is only partly
scanned or in case of an emergency operation when
too much surface tissue is damaged.
Rigid motions in R
3
have six degrees of freedom.
The general strategy of our algorithms can be sum-
marized as follows: first the translational component
of the rigid motion is fixed by mapping the measured
characteristic point onto the characteristic point on the
surface. The remaining degrees of freedom are deter-
mined by iteratively choosing the direction
~
d of a ro-
tation axis through the characteristic points from a set
of allowed directions (two degrees) and the last degree
is determined by rotating around this axis. The last
part, the rotation around the axis, is computed by us-
ing an algorithm presented in (Dimitrov et al., 2006)
(an outline of this algorithm is given later). After eval-
uating the quality of such a registration, the size of
the set of allowed directions is reduced by excluding
a neighborhood around
~
d based on the quality of the
computed registration and a new direction is chosen.
This process terminates after a certain constraint is
fulfilled, see section 1.4.
1.1 Problem Description and Notation
Let S ⊂ R
3
be a surface consisting of n triangles, rep-
resenting the anatomic model of the patient, and let
P ⊂ R
3
be a point set consisting of k points measured
from the patient (usually k ≪ n). Furthermore let
S
c
⊂ S be a set of points on the surface (which will
be called characteristic points). We think of points
s ∈ S
c
as representing some characteristic anatomic
feature of the patient (e.g., the root of the nasal bone).
The corresponding set of characteristic points in the
measured point set P is called P
c
⊂ P.
Definition 1.1 (optimal registration for a transforma-
tion class). Given a triangulated surface S , a point
set P and characteristic points on the model S
c
⊂ S
and in the point set P
c
⊂ P. A transformation t
opt
is
called optimal for a transformation class T if
t
opt
∈ argmin
t∈T

max

~
H(t(P
c
),S
c
),
~
H(t(P), S )

Here,
~
H(A, B) denotes the directed Hausdorff dis-
tance of a compact set A ⊂ R
3
to a compact set
B ⊂ R
3
. It is defined as
~
H(A, B) := max
a∈A
min
b∈B
ka− bk ,
where ka − bk is the Euclidean distance of a and b in
R
3
.
We investigate a slightly modified problem by
looking at scenarios where S
c
= {s} as well as P
c
=
{p} consist of a single characteristic point and where
the transformation class is restricted to the class of
all rigid motions t which map p upon s. A solution
minimizing the directed Hausdorff distance of P to S
under this restriction is called semioptimal.
Definition 1.2 (semioptimal matching with a single
characteristic point). Let p and s be the characteristic
points of P and S , respectively, and let T
s
⊂ T be the
set of rigid motions that map p onto s, i.e., t(p) = s.
A matching t
sopt
is called semioptimal if
t
sopt
= argmin
t∈T
s
~
H(t(P),S ).
1.2 Solving the Problem with Two
Characteristic Points
A related matching problem where both P and S have
two characteristic points was considered in (Dimitrov
et al., 2006). Since the correspondence between two
pairs of characteristic points is not enough to resolve
all six degrees of freedom of rigid motions in R
3
, the
semioptimal matching with two characteristic points
was considered, which has only one degree of free-
dom.
Definition 1.3 (semioptimal matching for two charac-
teristic points). Let p
1
, p
2
and s
1
,s
2
be the character-
istic points of P and S , respectively, and let T
s
⊂ T
be the set of rigid motions which centrically align the
line segment p
1
, p
2
with the line segment s
1
,s
2
. A
matching t
sopt
is called semioptimal if
t
sopt
= argmin
t∈T
s
~
H(t(P),S ).
p
1
+p
2
2
=
s
1
+s
2
2
p
1
p
2
s
1
s
2
Figure 1: Points p
1
, p
2
, s
1
, s
2
are centrically aligned, if all
points lie on a line and the midpoints of the line segments
p
1
, p
2
and s
1
,s
2
lie upon each other.
After centrically aligning p
1
to s
1
and p
2
to s
2
(see
Figure 1) only the rotational part of t
sopt
around the
axis s
1
,s
2
has to be determined. An algorithm for
computing such a semioptimal matching (Dimitrov
et al., 2006) runs in O(knlog
2
kn) time. We refer to
this algorithm as Alg
2
. It was shown that the quality
of the semioptimal matching (compared to the opti-
mal matching) depends on the relative spread of the
characteristic points with respect to P. In our setting
APPROXIMATE POINT-TO-SURFACE REGISTRATION WITH A SINGLE CHARACTERISTIC POINT
189

this algorithm provides a 4-approximation to the op-
timum.
We restrict our attention to semioptimal solutions be-
cause perturbation-based approximation schemes can
be used to compute solutions that are arbitrary close
to the optimum starting from a semioptimal configu-
ration (Dimitrov et al., 2006).
1.3 The General Strategy
In the following sections we present algorithms,
which approximate the registration problem with a
single characteristic point by sequentially fixing the
degrees of freedom of the desired registration. The
first three degrees, the translational part of the regis-
tration is determined by taking the vector difference
of the characteristic points p and s. The remaining
three degrees are computed in an iterative fashion.
The remaining degrees of freedom can be described
as determining the direction of a rotation axis through
s and the rotation around this axis. We repeatedly
choose an axis and determine the best rotation around
this axis. By evaluating the quality of this registra-
tion we are able to exclude an area around the rota-
tion axis from the parameter space and pick the next
axis. For the last part, the rotation around an axis
through the characteristic points, we introduce the no-
tion of virtual characteristicpoints. Virtual character-
istic points are auxiliary points in P and on S which
extend the input for the one-point case to an input for
Alg
2
. Given the characteristic point p ∈ P, we choose
as the virtual characteristic point the furthest point
ˆp = argmax
p
′
∈P
kp − p
′
k to p in P. For the virtual
characteristic point in the model space we repeatedly
choose points ˆs with distance kp − ˆpk to s. The line
segment s, ˆs is the axis around which P is rotated. This
process is iterated until a certain quality constraint is
fulfilled.
Definition 1.4 (distance function). Let
Alg
2
(S , P, (s, ˆs), (p, ˆp)) be the set of rigid mo-
tions computed by Alg
2
if ˆp and ˆs are added to the
input as virtual characteristic points for P and S
respectively. The distance function
~
H
sopt
: R
3
→ R is
defined as
~
H
sopt
( ˆs) := min
t∈Alg
2
(S ,P,(s, ˆs),(p, ˆp))
~
H(t(P), S ).
The term quality of a transformation and quality
of a virtual characteristic point is defined dual to the
term distance function: the quality is maximized, if
the distance function is minimized and vice versa.
1.4 The Approximation Settings with a
Single Characteristic Point
After fixing the translational part of the registration
two tasks remain: finding a rotation axis and finding
the right rotation around this axis. We call the set
of allowed directions for the rotation axis the search
space. For a characteristic point s a search space R
can be represented as the set of virtual characteristic
points ˆs ∈ R
3
for S , where each direction is defined by
the line segment through s and ˆs. For a search space
R let ε
R
= min
ˆs∈R
~
H
sopt
( ˆs) be the quality of the best
possible solution for the rotation around this axis as
determined by Alg
2
.
We present approximation algorithms for the follow-
ing two problems in two scenarios: In the first sce-
nario the search space is given by the intersection of
a sphere S
r
with radius r = kp− ˆpk centered in s with
the surface S , in the second scenario the search space
is given as the set of all points on S
r
. In the first sce-
nario we only consider registrations that map ˆp ex-
actly into S where in the second scenario we also in-
vestigate transformations which map ˆp close to S .
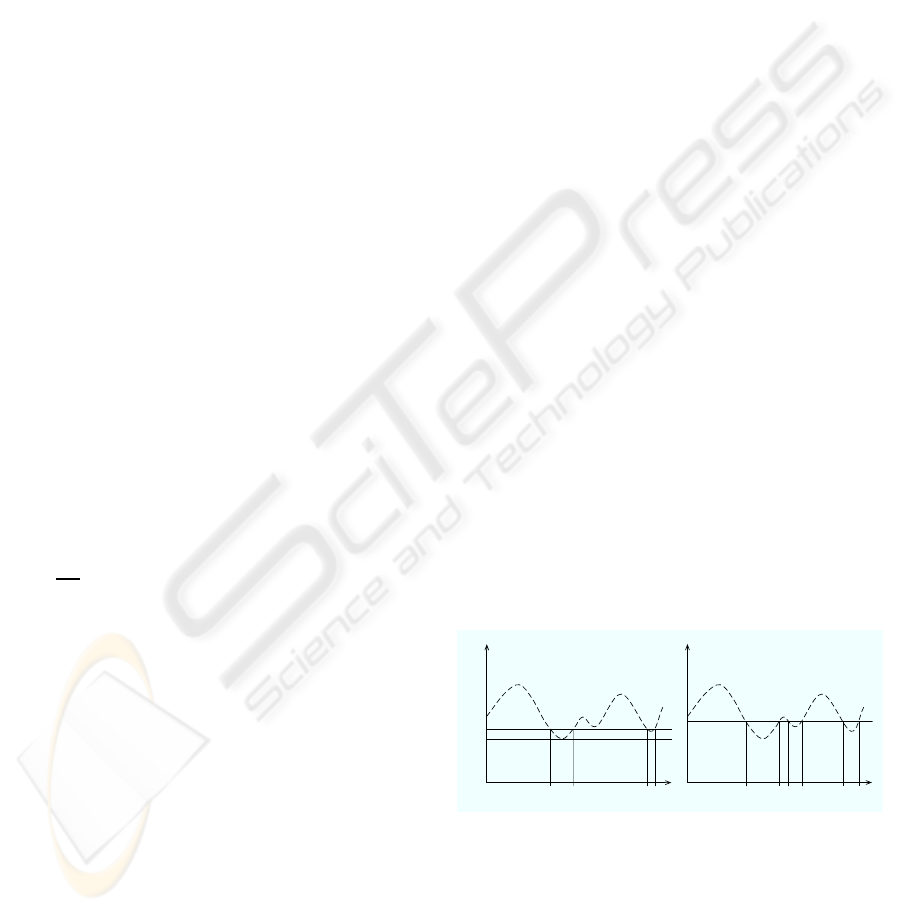
Problem 1.1. For an approximation parameter ∆, de-
termine the set Q ⊂ R of virtual characteristic points
such that
max
ˆs∈Q
~
H
sopt
( ˆs) ≤ ε
R
+ ∆.
The second problem arises in applications, where
an absolute upper bound for the quality of the regis-
tration is required:
Problem 1.2. For an upper bound ∆ for the quality of
a matching, determine the set Q ⊂ R of virtual char-
acteristic points such that:
∀ ˆs ∈ Q :
~
H
sopt
( ˆs) ≤ ∆.
0
0
H(C(λ))
H(C(λ))
a)
b)
ǫ
R
ǫ
R
+ ∆
R
R
⊂ Q
⊂ Q
⊂ Q
⊂ Q
⊂ Q
Figure 2: a) Illustration of Problem 1.1 b) Illustration of
Problem 1.2.
Using the initial translation of P which maps p
onto s, the computed set Q of valid directions for the
rotation axis, and their corresponding rotation angles
(computed by Alg
2
) we report a dense representation
of all rigid registrations which satisfy the properties
stated above.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
190

2 THE SEMIOPTIMAL
SOLUTION FOR A SINGLE
CHARACTERISTIC POINT
The following proposition gives a guaranty on the
quality of the semioptimal matching with a single
characteristic point.
Proposition 2.1. Any semioptimal matching in the 1-
point case is a 2-approximation of the optimal match-
ing.
Proof. Let ε
opt
be the value of the optimal solution
t
opt
and lett
a
be the translation that mapst
opt
(p) to s=
t
sopt
(p). Since kt
opt
(p) − sk = kt
opt
(p) − t
sopt
(p)k ≤
ε
opt
, the transformation t
a
◦t
opt
moves each point of P
at most ε
opt
far from its optimal position. Therefore,
~
H(t
sopt
(P),S ) ≤
~
H(t
a
◦ t
opt
(P),S )
≤
~
H(t
opt
(P),S ) + ε
opt
≤ 2ε
opt
Computing the semioptimal matching exactly. Let
t be a translation that maps p to s, and let Γ be the set
of all rotations around the point s. We are looking for
the rotation r
s
= argmin
r∈Γ
~
H(r ◦t(P),S ). We denote
by B
j
the ball with center t(p) and radius kp − p
j
k,
for p
j
∈ P \ {p}. Let f
j
denote the distance function
between B
j
and S . The function f
j
is the lower enve-
lope of the n distance functions between B
j
and each
triangle from S . Finding r
s
corresponds to computing
a minimum of the upper envelope f of the functions
f
1
,.. . , f
k−1
.
To determine the description complexity of f, it is
necessary to apply the theory of Davenport-Schinzel
sequences (Agarwal and Sharir, 1995). Because the
detailed analysis is beyond the scope and space of this
paper, we only mention the main facts. Since each
function f
j
is the lower envelope of n distance func-
tions between a ball and a triangle, it can be described
piecewise by trivariate polynomials of degree 4. The
complexity of the lower envelope of n such polynomi-
als is related to Davenport-Schinzel sequence whichs
maximal length is bounded from above by
˜
O(n
3
),
where
˜
O is standard O-notation that ignores the pa-
rameters that influence the constant of proportional-
ity, see (Agarwal and Sharir, 1995, Theorem 7.17)
for details. Thus, f is an upper envelope of
˜
O(n
3
k)
trivariate polynomials of degree 4, and its combinato-
rial complexity is
˜
O(n
9
k
3
). The envelope f can be
computed in a randomized expected time
˜
O(n
9
k
3
),
see (Agarwal and Sharir, 1995, Theorem 7.25) for de-
tails.
Moreover the time complexity presented above
holds only under the assumption that there is an ap-
propriate computational model that is able to find the
zeros of trivariate polynomials of degree 4 in a con-
stant time. Since no analytical or any other kind of
solution that needs a constant time to solve that prob-
lem is known, we therefore draw our attention to ap-
proximation algorithms.
3 APPROXIMATING THE
REGISTRATION FOR A
SINGLE CHARACTERISTIC
POINT
In this section we present algorithms that convert the
input for the one-point problem to instances of the
two-point problem by selecting appropriate virtual
characteristic points. These instances are then solved
using algorithm Alg
2
.
The central task is to find a suitable position for the
virtual characteristic point ˆs on S . Suitable in this
context means, that under the restriction that p is
mapped onto s and ˆp mapped to ˆs the distance func-
tion for Alg
2
is minimized. We show that the slope
of the distance function in the parameter space with
regard to the selected virtual characteristic point ˆs is
bounded to lie within [−1, 1] and how this fact can be
used to exclude parts of the search space.
3.1 The Lipschitz Constant of the
Distance Function
Lemma 3.1. Let S , s,P, p be as above. For any two
points ˆs
1
, ˆs
2
∈ R
3
with ks− ˆs
1
k = ks− ˆs
2
k = kp − ˆpk
the following holds:



~
H
sopt
( ˆs
1
) −
~
H
sopt
( ˆs
2
)



≤ k ˆs
1
− ˆs
2
k.
Proof. Assume that t ∈ A(S ,P,(s, ˆs
1
),(p, ˆp)) is one
of the transformations mapping p to s and ˆp to ˆs
1
and
let ρ be a rotation around s mapping ˆs
1
to ˆs
2
. Since
ˆp is a farthest point from p, we have for any point
p
′
∈ P:
kρ ◦t(p
′
) − t(p
′
)k ≤ kρ◦ t( ˆp) −t( ˆp)k = k ˆs
1
− ˆs
2
k.
Consequently
~
H
sopt
( ˆs
2
) ≤
~
H(ρ ◦ t(P),S ) ≤
~
H(t(P),S ) + k ˆs
1
− ˆs
2
k =
~
H
sopt
( ˆs
1
) + k ˆs
1
− ˆs
2
k.
A symmetric argument provides that
~
H
sopt
( ˆs
1
) ≤
~
H
sopt
( ˆs
2
) + k ˆs
1
− ˆs
2
k.
Let S
r
be the sphere centered in s with radius
r = kp − ˆpk. Lemma 3.1 states that moving a virtual
characteristic point ˆs
1
to a point ˆs
2
on S
r
, changes the
value of the distance function by at most k ˆs
1
− ˆs
2
k.
APPROXIMATE POINT-TO-SURFACE REGISTRATION WITH A SINGLE CHARACTERISTIC POINT
191

This bound on the Lipschitz constant of the distance
function can be used to exclude parts of the parame-
ter space around a virtual characteristic point, because
it describes by which amount the fuction value can
change within the neighborhood around this point.
3.2 Approximation Strategies for
One-dimensional Search Spaces
To illustrate the idea of our approximation techniques
we first consider the case where the search space R is
one-dimensional. We are interested in virtual charac-
teristic points ˆs that are kp− ˆpk close to s. Therefore,
we choose this search space to be the intersection C
of the triangulated surface S with S
r
. This is the sce-
nario where all virtual characteristic points ˆs ∈ C map
ˆp exactly onto the surface.
The intersection C consists of a set of curves and
each curve consists of a sequence of circular patches
(possibly closed), where each patch results from the
intersection of the sphere S
r
with a single triangle
of the model. The task is to determine those parts
on each curve that provide good virtual characteris-
tic points. Good virtual characteristic points ˆs have
the property that either |
~
H
sopt
( ˆs) − ε
R
| ≤ ∆ (Problem
1.1) or that
~
H
sopt
( ˆs) is below a given threshold (Prob-
lem 1.2). This is achieved by probing several points
on the curve and, depending on the value of the dis-
tance function for these virtual characteristic points,
exclude parts of the neighborhoodaround these points
from R.
Let q
C
be an endpoint of curve C ∈ C (if C is
closed, we cut C open at an arbitrary position q
C
) and
parametrize each point onC by its arclength to q
C
. Let
C(λ) denote the point on C with arclength λ from q
C
.
Recall that according to Lemma 3.1 moving a point ˆs
by ∆
λ
on S
r
changes the quality of the registration by
at most ∆
λ
.
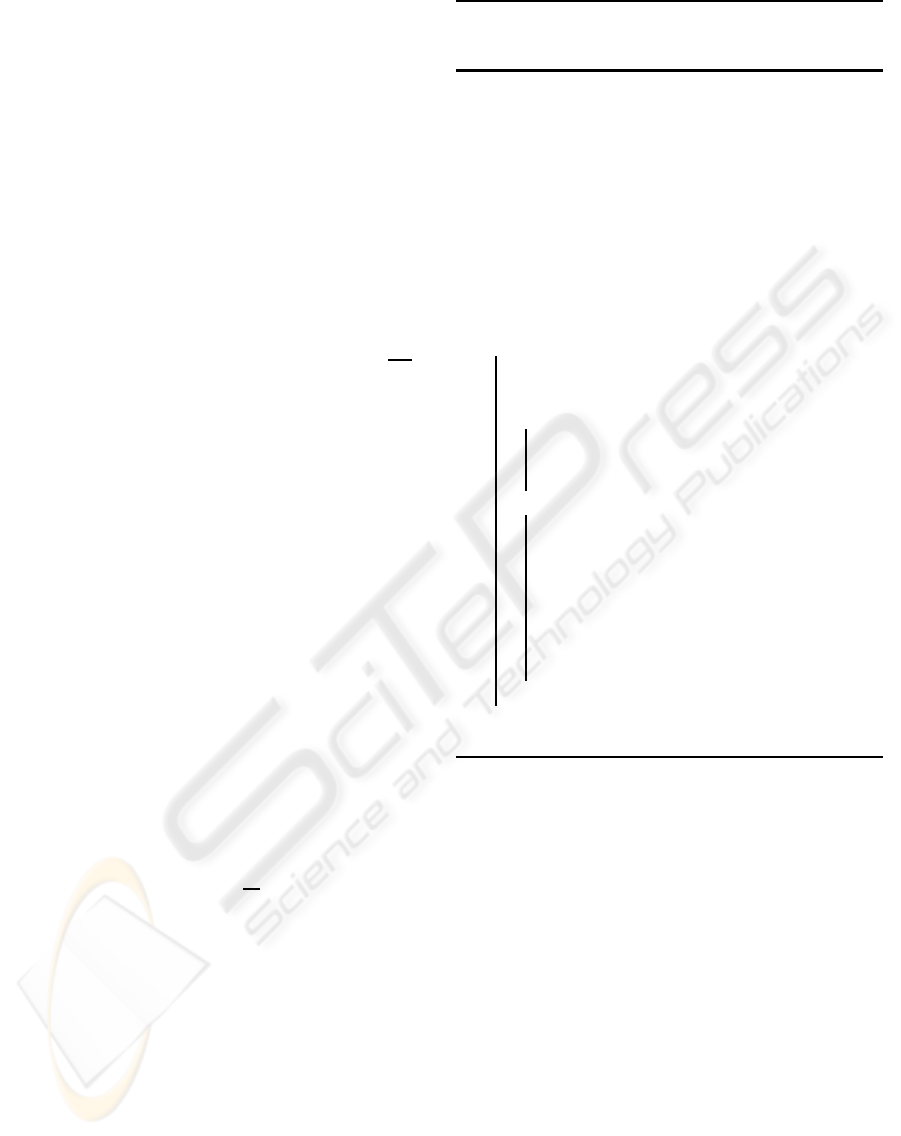
Corollary 3.1. For two points C(λ),C(λ + ∆) on a
curve C ⊂ S
r
with an arclength distance of ∆, the fol-
lowing holds (see Fig. 3 a):



~
H
sopt
(C(λ)) −
~
H
sopt
(C(λ + ∆))



≤ ∆
Depending on the quality of a probe point ˆs one
can exclude parts of its neighborhoodin the parameter
space. This can be used to bound the value of the dis-
tance function between two probe points, as accord-
ing to Lemma 3.1 the scope in any point of the graph
lies within [−1, 1].
Solving Problem 1.1: The Lipschitz constant of the
distance function can be used to bound the number of
samples needed to provide an absolute approximation
∆
≤ ∆
0
λ
0
λ
∆
2(∆ − ǫ
λ
′′
)
2(ǫ
λ
′
− ∆)
λ
′
λ
′′
H(C(λ))
H(C(λ))
a)
b)
Figure 3: a) The quality of two points with arclength dis-
tance ∆ differs by at most ∆, b) The ex- and inclusion areas
for two probing positions with parameter λ
′
(left exclusion
area) and λ
′′
(right inclusion area).
to ε
R
= min
ˆs∈R
~
H
sopt
( ˆs). The idea is to sample and test
a set Q ⊂ R of virtual characteristic points until ε
R
is
known to differ by at most ∆ from the best quality
of a sampled point. The number of samples needed
to ensure that min
ˆs∈Q
~
H
sopt
( ˆs) − ε
R
≤ ∆ is maximal if
the distance function is constant on C. We have that:
max
λ
′
∈[λ,λ+∆]



~
H
sopt

C(λ
′
)

− m
λ



≤ ∆
where m
λ
= min
n
~
H
sopt
(C(λ)),
~
H
sopt
(C(λ + ∆))
o
.
Corollary 3.2. Let the set of curves C = {C
0
,.. . ,C
i
}
induced by the intersection of S and S
r
with a total
arclength of L be the search space R. Providing that
min
ˆs∈Q

~
H
sopt
( ˆs) − ε
R

≤ ∆ there is a probe set Q
which size is bounded by O

L
∆

.
Solving Problem 1.2: The second section deals
with determining all virtual characteristic points ˆs
and their corresponding registrations which satisfy
~
H
sopt
( ˆs) ≤ ∆ for a given quality ∆. As in the previ-
ously discussed problem the bound on the slope of
the distance function allows us to exclude a neighbor-
hood of a probe ˆs from the search space or to include
a neighborhood to the solution, depending on the dif-
ference
~
H
sopt
( ˆs) − ∆. Let C(λ) be a sample point
on a curve C with parameter λ and distance value
~
H
sopt
(C(λ)) = ε
λ
. The size of the in- or exclusion
area depends on the difference of ε
λ
and ∆ (see also
Fig. 3 b):
ε
λ
− ∆ > 0: The quality of the best registration if
C(λ) is chosen as the virtual characteristic point
for S is above ∆. The next sample points ˆs on C
with the property that
~
H
sopt
( ˆs) ≤ ∆ have a distance
to C(λ) of at least |ε
λ
− ∆| in parameter space.
ε
λ
− ∆ ≤ 0: The point C(λ) and all points ˆs in its
∆ − ε
λ
neighbourhood have the property that
~
H
sopt
( ˆs) ≤ ∆ and can therefore be included in the
solution set.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
192

Robustness. This approach is sensitive to noise on
P, especially to the influence of noise on the dis-
tance r = kp− ˆpk, which determines the radius of the
sphere S
r
. A slight pertubation of p or ˆp could pre-
vent S
r
from intersecting S , which leaves the set of
possible virtual characteristic points empty.
3.3 Approximation Strategies for
Two-dimensional Search Spaces
In this section we describe variants of the approxima-
tion strategies of Section 3.2 and extend the search
space R to the whole sphere S
r
. By fixing a virtual
characteristic point ˆs ∈ S
r
we determine an axis l = s, ˆs
around which P is rotated to find the best semiopti-
mal solutions. Using this search space increases the
robustness of our approach against noise on P.
Solving Problem 1.1: We want to determine a set
Q ⊂ R of virtual characteristic points, such that
min
q∈Q
~
H
sopt
(q)−min
q∈R
~
H
sopt
(q) ≤ ∆. Such a probe
set Q has the property that the search space S
r
is com-
pletely contained in the union of all balls with radius
∆, centered in a sample point q ∈ Q . In other words
any probe set Q ⊂ S
r
satisfying
∀a ∈ S
r
∃ ˆs ∈ Q ka− ˆsk ≤ ∆
is a valid probe set.
Corollary 3.3. There is a non empty sample set Q
which provides that min
ˆs∈Q
~
H
sopt
( ˆs) − ε
R
≤ ∆ for R =
S
r
whose size is bounded by O

r
2
∆
2

, for r = kp− ˆpk.
Solving Problem 1.2: As in the previoussection we
want to compute the set Q =
n
ˆs ∈ S
r
|
~
H
sopt
( ˆs) ≤ ∆
o
.
To this end, we sample points ˆs of S
r
and depending
on the value of
~
H
sopt
( ˆs) exclude regions in the neigh-
borhood of ˆs from the search space or add a region to
the solution. Recall that
~
H
sopt
( ˆs
2
) ≥
~
H
sopt
( ˆs
1
) − ∆ for
any ˆs
2
with kˆs
1
− ˆs
2
k ≤ ∆ and if
~
H
sopt
( ˆs
1
)−∆ < 0, all
points ˆs
2
in the intersection of S
r
with a ball centered
at ˆs
1
with radius ∆ −
~
H
sopt
( ˆs
1
) have the property that
~
H
sopt
( ˆs
2
) ≤ ∆ and can therefore be included in the
solution set. These observations lead to Algorithm 1.
Algorithm 1: Computing the set of virtual char-
acteristic points providing an absolute error reg-
istration
Data: The model S , its characteristic point
s ∈ S , the set of measured points P, their
characteristic point p ∈ P, an absolute
error approximation value ∆.
Result: The set Q of virtual characteristic
points realizing a distance function
value of at most ∆.
// initializing the result set
Q :=
/
0;1
// candidate probe set to S
r
M := S
r
;2
while M 6=
/
0 do3
// select a random point
ˆs := takeRandomPoint(M);4
if
~
H
sopt
( ˆs) − ∆ > 0 then5
// exclude neighborhood
M := M \

S
r
∩ Ball( ˆs,
~
H
sopt
( ˆs) − ∆)

;
77
else8
// include neighborhood
// compute intersection
I := S
r
∩ Ball( ˆs, ∆−
~
H
sopt
( ˆs));1010
// remove I from search space
M := M \ I;11
// add I to solution
Q := Q ∪ I;12
end13
end14
return Q ;15
The function Ball(c,r) (lines 7 and 10) computes
a ball with radius r centered in c.
Algorithm 1 computes all points ˆs on S
r
with
~
H
sopt
( ˆs) ≤ ∆. The practicability of Algorithm 1 is
quite limited, as it needs to maintain an arrangement
of circles on a sphere which is by itself a challenging
problem. The methods currently known to compute
such arrangements are too time consuming to be used
in a medical navigation system (Cazals and Loriot,
2007).
4 AN IMPLEMENTATION FOR
TWO-DIMENSIONAL SEARCH
SPACES
As the computation of the arrangement of circles on
a sphere is complex and time consuming, we present
a simple and efficient implementation of Algorithm 1
which uses quadtrees (de Berg et al., 1997) to approx-
APPROXIMATE POINT-TO-SURFACE REGISTRATION WITH A SINGLE CHARACTERISTIC POINT
193

imate the arrangement: The information about areas
that are excluded from the search space is maintained
not on S
r
but on six quadtrees which are placed on
each side of an axis-parallel cube surrounding S
r
.
4.1 The Implementation
The implementation proceeds round based and each
round consists of the following steps: Consider the
smallest axis parallel cube B
r
which contains S
r
. First
a point ˆs is selected from a side of B
r
by an heuris-
tic described later. Then this point is projected down
onto a point ˆs
′
on S
r
. For ˆs
′
we call Alg
2
and compute
the distance value
~
H
sopt
( ˆs
′
) and by taking the differ-
ence of
~
H
sopt
( ˆs
′
) − ∆ we determine the radius of the
in-/ exclusion balls around ˆs
′
. Finally this ball is pro-
jected back onto B
r
and the quadtrees which maintain
the in- and excluded areas on B
r
are refined to approx-
imate the projected ball.
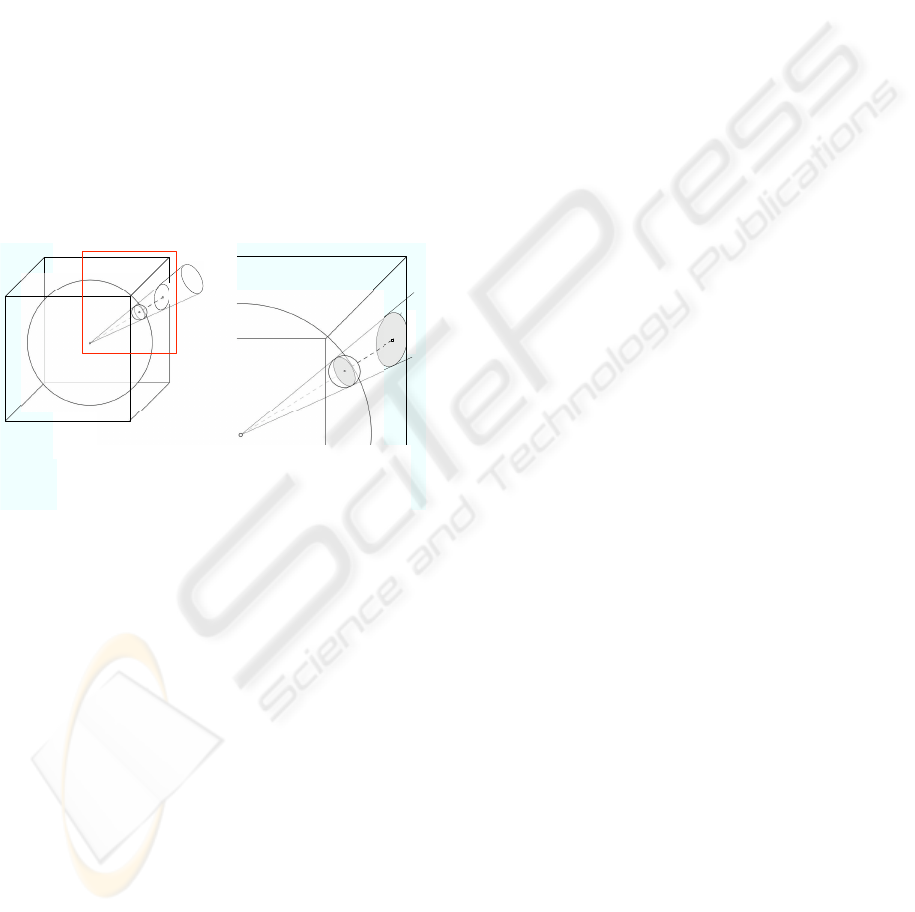
S
r
M
r
s
s
M
r
S
r
b)
a)
b
t
e
t
ˆs
t
ˆs
′
t
Figure 4: The ball b
r
with radius |
~
H
sopt
(q
′
t
) − ∆| intersects
the sphere S
r
in a circle on which is then projected onto B
r
.
In Detail. In each round of the algorithm we deter-
mine a facet t of a quadtree and its center ˆs
t
. The
probe point ˆs
′
t
for this position is computed by inter-
secting S
r
with the ray starting in s passing through
ˆs
t
. The difference of
~
H
sopt
( ˆs
′
t
) − ∆ defines the radius
of an inclusion (in case of
~
H
sopt
( ˆs
′
t
) − ∆ ≤ 0) or an
exclusion (in case of
~
H
sopt
( ˆs
′
t
) − ∆ > 0) ball b
t
cen-
tered in ˆs
′
t
. All sample points ˆs in the intersection of
b
t
with S
r
either fulfill
~
H
sopt
( ˆs) ≤ ∆ and can therefore
be added to the solution set or can be discarded other-
wise. This information has to be propagated onto the
sides of B
r
in order to adjust the quadtrees on its sides.
To this end we determine the intersection e
t
of B
r
with
the cone, whose apex is s and that touches the border
of the intersection of b
t
with S
r
(see Fig. 4). All facets
of the quadtrees intersected by e
t
are subdivided until
they are either not intersected by e
t
anymore or have
an area below a reasonable threshold.
Note that the projection of points from B
r
to S
r
is not
distance preserving: two points on a side and close to
a corner of B
r
have a larger distance to each other after
being projected onto S
r
than two points that lie closer
to a midpoint of a side of B
r
. This effect is compen-
sated by the backward projection of b
t
onto the sides,
as the area of e
t
depends on the distance of ˆs
t
to the
closest corner of B
r
.
Figure 5 shows screen shots of the implementation at
the moment where the first inclusion area was found.
A Heuristic for Choosing the next Sample Point.
To determine which facet to choose for the next
sample point we introduce a max-area heuristic. Each
facet of the quadtree has a priority and in addition is
labeled either as included , excluded or unknown .
If the label of a facet is unknown , the priority is set
to the area of the facet and set to −∞ otherwise.
Each quadtree is initialized with one facet, a side of
B
r
, labeled unknown . All facets of the six quadtrees
with label unknown are furthermore stored in a single
max priority queue (the order of facets with the same
priority is arbitrary). Facets that are covered by e
t
are
labeled either included or excluded , depending on
whether e
t
is an in- or exclusion area. Facets labeled
included are added to the solution set. In each round
the facet with the highest priority is chosen, as we
expect the area of sample points with quality to be
small and accordingly the exclusion areas to be large.
Facets that are completely covered by e
t
are la-
beled corresponding to the sign of the difference
~
H
sopt
( ˆs
′
t
) − ∆. All new facets that are not intersected
by e
t
are labeled unknown and are inserted into the
priority queue, according to their area.
The algorithm terminates after either all leaves are
labeled or under the given threshold or a certain num-
ber of rounds is reached.
4.2 Evaluation
We implemented the algorithm as described in Sec-
tion 4.1 and evaluated the performance on a intel-core
2 duo computer with 2GB central memory. The com-
putations on a model with about three thousand tri-
angles and a point set P consisting of 8 points, both
scaled to fit into the unit cube, took on average 25.31
seconds.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
194

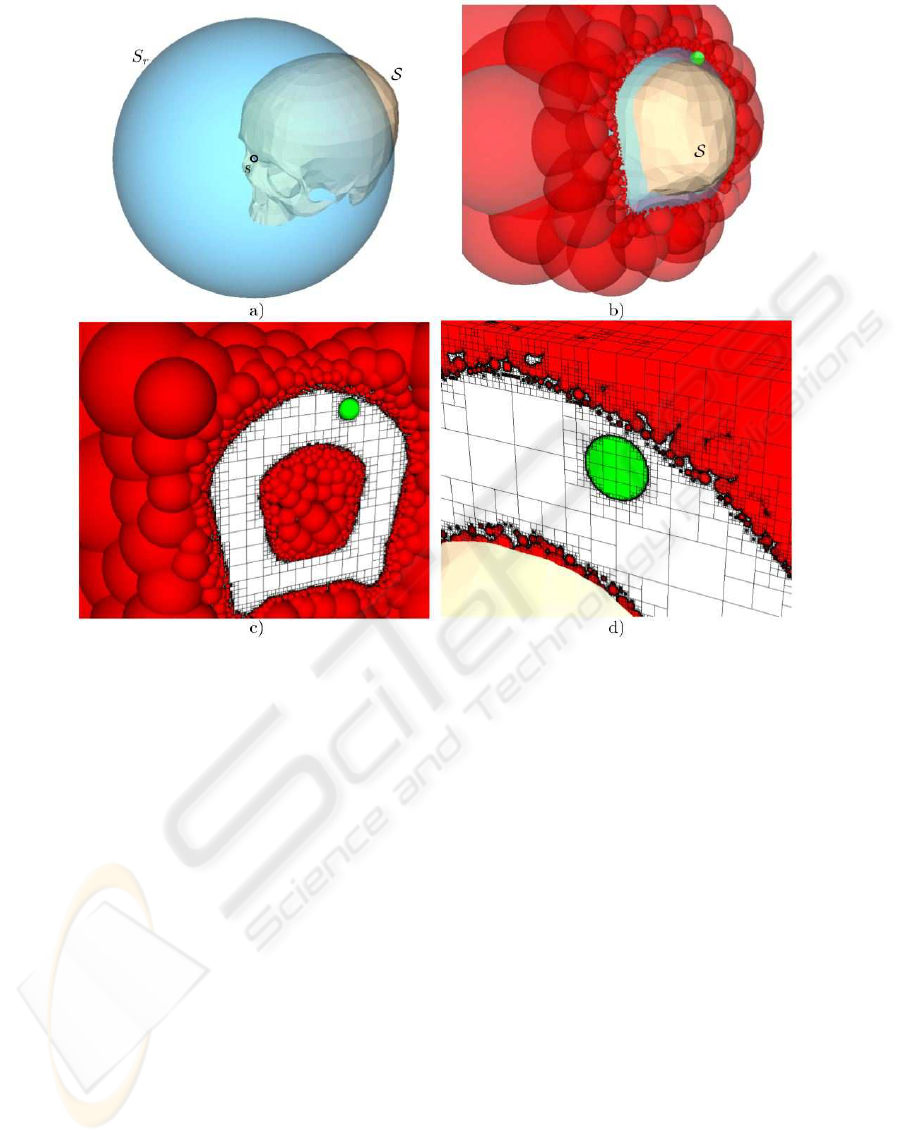
Figure 5: Screen shots of the implementation in the moment where the first inclusion area is found: a) the model S , its
characteristic point s and the sphere S
r
. b) the back of the model and the exclusion (dark gray/red) and inclusion (light
gray/green) balls, some exclusion areas are hidden by the model c) the projected error balls, parts of the surrounding cube
B
r
with the quadtree structure on its sides d) a part of the model in the lower left corner and the quadtree refinement with
included (light gray/green) and excluded areas (dark gray/red).
REFERENCES
Agarwal, K. P. and Sharir, M. (1995). Davenport–schinzel
sequences and their geometric applications. Technical
report, Durham, NC, USA.
Cazals, F. and Loriot, S. (2007). Computing the exact ar-
rangement of circles on a sphere, with applications in
structural biology: video. In SCG ’07: Proc. 23rd
Annu. ACM Sympos. on Comput. Geom., pages 119–
120.
Chui, H. and Rangarajan, A. (2003). A new point matching
algorithm for non-rigid registration. In Computer Vi-
sion and Image Understanding archive, vol. 89, pages
114–141.
de Berg, M., van Kreveld, M., Overmars, M., and
Schwarzkopf, O. (1997). Computational Geometry:
Algorithms and Applications. Springer-Verlag.
Dimitrov, D., Knauer, C., and Kriegel, K. (2006). Regis-
tration of 3d - patterns and shapes with characteristic
points. In Proc. of International Conference on Com-
puter Vision Theory and Applications - VISAPP 2006,
pages 393–400.
Dimitrov, D., Knauer, C., Kriegel, K., and Stehn, F.
(2007). Approximation algorithms for a point-to-
surface registration problem in medical navigation. In
Proc. Frontiersin Algorithmics Workshop - FAW 2007,
pages 26–37.
Matth¨aus, L., Giese, A., Trillenberg, P., Wertheimer, D., and
Schweikard, A. (2006). Solving the positioning prob-
lem in TMS. In GMS CURAC, vol. 1.
Wang, Y., Peterson, B., and Staib, L. (2000). Shape-based
3D surface correspondence using geodesics and local
geometry. In Comp. Vision Pattern Recog., vol. 2,
pages 644–651.
APPROXIMATE POINT-TO-SURFACE REGISTRATION WITH A SINGLE CHARACTERISTIC POINT
195