PERFORMANCE EVALUATION OF ROBUST MATCHING

MEASURES

Federico Tombari, Luigi Di Stefano, Stefano Mattoccia and Angelo Galanti

University of Bologna - Department of Electronics Computer Science and Systems (DEIS)

Viale Risorgimento 2, 40136 - Bologna, Italy

University of Bologna - Advanced Research Center on Electronic Systems (ARCES)

Via Toffano 2/2, 40135 - Bologna, Italy

Keywords:

Robust matching measure, template matching, performance evaluation.

Abstract:

This paper is aimed at evaluating the performances of different measures which have been proposed in lit-

erature for robust matching. In particular, classical matching metrics typically employed for this task are

considered together with speciﬁc approaches aiming at achieving robustness. The main aspects assessed by

the proposed evaluation are robustness with respect to photometric distortions, noise and occluded patterns.

Speciﬁc datasets have been used for testing, which provide a very challenging framework for what concerns

the considered disturbance factors and can also serve as testbed for evaluation of future robust visual corre-

spondence measures.

1 INTRODUCTION

One of the most important tasks in computer vision is

visual correspondence, which given two sets of pixels

(i.e. two images) aims at ﬁnding corresponding pixel

pairs belonging to the two sets (homologous pixels).

As a matter of fact, visual correspondence is com-

monly employed in ﬁelds such as pattern matching,

stereo correspondence, change detection, image reg-

istration, motion estimation, image vector quantiza-

tion.

The visual correspondence task can be extremely

challenging in presence of disturbance factors which

can typically affect images. A common source of dis-

turbancescan be related to photometric distortions be-

tween the images under comparison. These can be

ascribed to the camera sensors employed in the im-

age acquisition process (due to dynamic variations of

camera parameters such as auto-exposure and auto-

gain, or to the use of different cameras), or can be

induced by factor extrinsic to the camera, such as

changes of the amount of light emitted by the sources

or viewing of non-lambertian surfaces at different

angles. Other major disturbance factors are repre-

sented by distortions of the pixel intensities due to

high noise, as well as by the presence of partial oc-

clusions.

In order to increase the reliability of visual cor-

respondence many matching measures aimed at be-

ing robust with respect to the above mentioned

disturbance factors have been proposed in litera-

ture. Evaluation assessments have also been pro-

posed whichcompared some of these measures in par-

ticular ﬁelds such as stereo correspondence (Cham-

bon and Crouzil, 2003), image registration (Zitov´a

and Flusser, 2003) and image motion (Giachetti,

2000). Generally speaking, apart from classical

approaches which will be discussed in Section 2,

many robust measures for visual correspondencehave

been proposed in literature (Tombari et al., 2007),

(Crouzil et al., 1996), (Scharstein, 1994), (Seitz,

1989), (Aschwanden and Guggenbuhl,1992), (Martin

and Crowley, 1995), (Fitch et al., 2002), (Zabih and

Woodﬁll, 1994), (Bhat and Nayar, 1998), (Kaneko

et al., 2003), (Ullah et al., 2001). A taxonomy which

includes the majority of these approaches is proposed

in (Chambon and Crouzil, 2003).

This paper focuses on pattern matching, which

aims at ﬁnding the most similar instances of a given

pattern, P, within an image.In particular, this paper

aims at comparing traditional general purpose ap-

proaches together with proposals speciﬁcally con-

ceived to achieve robustness, in order to determine

which metric is more suitable to deal with distur-

bance factors such as photometric distortions, noise

and occlusions. More precisely, in the comparison

473

Tombari F., Di Stefano L., Mattoccia S. and Galanti A. (2008).

PERFORMANCE EVALUATION OF ROBUST MATCHING MEASURES.

In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 473-478

DOI: 10.5220/0001087304730478

 SciTePress

we will consider the following matching measures:

MF (Matching Function), i.e. the approach recently

proposed in (Tombari et al., 2007), GC (Gradient

Correlation), i.e. the approach initially proposed in

(Scharstein, 1994) according to the formulation pro-

posed in (Crouzil et al., 1996) for the pattern matching

problem, OC (Orientation Correlation), proposed in

(Fitch et al., 2002). Moreover, we will consider the

SSD (Sum of Squared Differences) and NCC (Nor-

malized Cross Correlation) measures applied on gra-

dient norms (G-NCC and G-SSD), which showed

good robustness against illumination changes in the

experimental comparison described in (Martin and

Crowley, 1995). The approach relying on gradi-

ent orientation only, proposed in (Seitz, 1989) and

successively modiﬁed in (Aschwanden and Guggen-

buhl, 1992), has not been taken into account since, as

pointed out in (Crouzil et al., 1996), it is prone to er-

rors in the case of gradient vectors with small mag-

nitude. Considered traditional measures are NCC,

ZNCC (Zero-mean NCC) and SSD: NCC and ZNCC

showed good robustness with respect to brightness

changes, on the other hand SSD showed good insen-

sibility toward noise (Aschwanden and Guggenbuhl,

1992), (Martin and Crowley, 1995).

All the considered proposals are tested on 3

datasets which represent a challenging framework

for what regards the considered distortions. These

dataset are publicly available

and they might serve

as a testbed for future evaluations of robust match-

ing measures. Before reporting on the experimen-

tal evaluation, all compared measures are brieﬂy de-

scribed. Furthermore, for what regards MF, the paper

also proposes some modiﬁcations to the original ap-

proach proposed in (Tombari et al., 2007), and ex-

ploits the proposed experimental evaluation to per-

form a behavioural analysis of this class of functions.

2 TRADITIONAL MATCHING

CRITERIA

Matching measures traditionally adopted in order to

compute the similarity between two pixel sets are

typically subdivided into two groups, given they are

based on an afﬁnity or distortion criterion. Afﬁnity

measures are often based on correlation, withthe most

popular metric being the Normalized Cross Correla-

tion (NCC). In a pattern matching scenario, being P

the pattern vector, sized M × N (width × height), I the

image vector, sized W × H, and I

the image subwin-

dow at coordinates (x, y) and having the same dimen-

Available at: www.vision.deis.unibo.it/pm-eval.asp

sions as P, the NCC function at (x, y) is given by:

NCC(x, y) =

∑

i=1

∑

j=1

P(i, j) ·I

(i, j)

∑

i=1

∑

j=1

(i, j) ·

∑

i=1

∑

j=1

(i, j)

(1)

As it can be seen, the cross-correlation between

P and I

is normalized by the L

norms of the two

vectors, in order to render the measure robust to any

spatially constant multiplicative bias. By subtracting

the mean intensity value of the pattern and of the im-

age subwindow we get an even more robust matching

measure:

ZNCC(x, y) =

∑

i=1

∑

j=1

(P(i, j) −

P) · (I

(i, j) −

)

∑

i=1

∑

j=1

(P(i, j) −

∑

i=1

∑

j=1

(i, j) −

)

(2)

where

P and

represent respectively the mean in-

tensity of P and I

. This measure is referred to as

Zero-mean NCC (ZNCC) and it is robust to spatially

constant afﬁne variations of the image intensities.

As regards the distortion criterion, the classical

measures are based on the L

distance between P and

. In particular, with p = 2 we get the Sum of Squared

Differences (SSD):

SSD(x, y) =

∑

i=1

∑

j=1



P(i, j) − I

(i, j)



(3)

While all these measures are usually computed di-

rectly on the pixel intensities of the image sets, in

(Martin and Crowley, 1995) it was shown that by

computing these measures on the gradient norm of

each pixel a higher robustness is attained, i.e. for what

concerns insensitivity to illumination changes G-SSD

and G-NCC showed to perform well. In particular, if

we denote with G

(i, j) the gradient of the pattern at

pixel (i, j):

(i, j) =



∂P(i, j)

∂i

∂P(i, j)

∂j



(i, j), G

(i, j)

(4)

and similarly with G

(i, j) the gradient of the image

subwindow at pixel (i, j):

(i, j) =



∂I

(i, j)

∂i

∂I

(i, j)

∂ j



(i, j), G

(i, j)

(5)

the gradient norm, or magnitude, in each of the

two cases is computed as:

||G

(i, j)|| =

(i, j)

+ G

(i, j)

(6)

||G

(i, j)|| =

(i, j)

+ G

(i, j)

(7)

i.e. || · || represents the L

norm of a vector. Hence the

G-NCC function can be deﬁned as:

G− NCC(x, y) =

∑

i=1

∑

j=1

||G

(i, j)|| · ||G

(i, j)||

∑

i=1

∑

j=1

||G

(i, j)||

∑

i=1

∑

j=1

||G

(i, j)||

(8)

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

474

and the G-SSD function as:

G− SSD(x, y) =

∑

i=1

∑

j=1



||G

(i, j)||− ||G

(i, j) ||



(9)

Since (Martin and Crowley, 1995) recommends to

compute the partial derivatives for the gradient com-

putation on a suitably smoothed image, in our imple-

mentation they will be computed by means of the So-

bel masks.

3 THE MF MEASURE

In (Tombari et al., 2007) a matching measure was pro-

posed which is implicitly based on the so-called or-

dering constraint, that is, under the assumption that

photometric distortions do not affect the order be-

tween intensities of neighbouring pixels. This is anal-

ogous to the assumption that the sign of the differ-

ence between a pair of neighbouring pixels should not

change in presence of this kind of distortions. For

this reason the proposed measure correlates the dif-

ferences between a set of pixel pairs deﬁned on P and

their correspondent ones on I

. In particular, the pairs

in each set include all pixels at distance 1 and 2 one

to another along horizontal and vertical directions. In

order to compute this set, we deﬁne a vector of pixel

differences computed at a point (i, j) on P:

1,2

(i, j) =







P(i− 1, j) − P(i, j)

P(i, j− 1) − P(i, j)

P(i− 1, j) − P(i+ 1, j)

P(i, j− 1) − P(i, j+ 1)







(10)

and, similarly, at a point (i, j) on I

1,2

(i, j) =







(i− 1, j) − I

(i, j)

(i, j− 1) − I

(i, j)

(i− 1, j) − I

(i+ 1, j)

(i, j− 1) − I

(i, j+ 1)







(11)

Hence, the MF function proposed in (Tombari

et al., 2007) consists in correlating these two vectors

for each point of the pattern and the subwindow, and

in normalizing the correlation with the L

norm of the

vectors themselves:

1,2

(x, y) =

∑

i=1

∑

j=1

1,2

(i, j) ◦ δ

1,2

(i, j)

∑

i=1

∑

j=1

1,2

(i, j) ◦ δ

1,2

(i, j) ·

∑

i=1

∑

j=1

1,2

(i, j) ◦ δ

1,2

(i, j)

(12)

where ◦ represents the dot product between two

vectors, and the normalization allows the measure to

range between [−1, 1].

Figure 1: The 3 considered sets of neighbouring pixel pairs.

It is a peculiarity of this method that, because of

the correlation between differences of pixel pairs, in-

tensity edges tend to determine higher correlation co-

efﬁcients (in magnitude) with respect to low-textured

regions. Thus, this can be seen as if the measure

mostly relies on the pattern edges. For this reason,

MF can be usefully employed also in presence of high

levels of noise, as this disturbance factor can typi-

cally violate the ordering constraint on low-textured

regions, but seldom along intensity edges. Similar

considerations can be made in presence of occluded

patterns.

The set of pixel pairs originally proposed in

(Tombari et al., 2007) can be seen as made out of two

subsets: the set of all pixels at distance 1 one to an-

other along horizontal and vertical directions, and the

set ofall pixels at distance 2 one to another along same

directions. Theoretically, the former should beneﬁt of

the higher correlation given by adjacent pixels, while

the latter should be less inﬂuenced by quantization

noise that is introduced by the camera sensor. We will

refer to the MF measure applied on each of the two

subsets as, respectively, MF

and MF

. For these last

two cases, once deﬁned the pixel differences relative

to the case of distance 1:

(i, j) =

P(i− 1, j) − P(i, j)

P(i, j− 1) − P(i, j)

(13)

(i, j) =

(i− 1, j) − I

(i, j)

(i, j− 1) − I

(i, j)

(14)

and the pixel differences relative to the case of dis-

tance 2:

(i, j) =

P(i− 1, j) − P(i+ 1, j)

P(i, j− 1) − P(i, j+ 1)

(15)

(i, j) =

(i− 1, j) − I

(i+ 1, j)

(i, j− 1) − I

(i, j+ 1)

(16)

it is straightforward to deﬁne the two novel measures

and MF

as:

PERFORMANCE EVALUATION OF ROBUST MATCHING MEASURES

475

(x, y) =

∑

i=1

∑

j=1

(i, j) ◦ δ

(i, j)

∑

i=1

∑

j=1

(i, j) ◦ δ

(i, j) ·

∑

i=1

∑

j=1

(i, j) ◦ δ

(i, j)

(x, y) =

∑

i=1

∑

j=1

(i, j) ◦ δ

(i, j)

∑

i=1

∑

j=1

(i, j) ◦ δ

(i, j) ·

∑

i=1

∑

j=1

(i, j) ◦ δ

(i, j)

A graphical representation of the 3 different pixel

pair sets used by MF

1,2

, MF

and MF

is shown in Fig. 1.

We believe that it is interesting to exploit the perfor-

mance evaluation proposed in this paper also with the

aim of determining if there is an optimal set between

these 3 or if, conversely, the measure has the same be-

haviour on all sets. This issue will be discussed in

Section 6.

4 THE OC MEASURE

The OC measure (Fitch et al., 2002) is based on the

correlation of the orientation of the intensity gradient.

In particular, for each gradient of the pattern G

(i, j)

a complex number representing the orientation of the

gradient vector is deﬁned as:

(i, j) = sgn(G

(i, j) + ι G

(i, j)) (17)

with ι denoting the imaginary unit and where:

sgn(x) =

(

0 if|x| = 0

|x|

otherwise

(18)

Analogously, a complex number representing the

orientation of the image subwindow gradient vector

(i, j) is deﬁned as:

(i, j) = sgn(G

(i, j) + ι G

(i, j)) (19)

As proposed in (Fitch et al., 2002), the partial

derivatives for the gradient computation are calcu-

lated by approximating them with the central differ-

ences. Hence, the OC measure between P and I

deﬁned as the real part of the correlation between all

gradient orientations belonging to P and I

OC(x, y) = Re{

∑

i=1

∑

j=1

(i, j) · O

∗

(i, j)} (20)

with ∗ indicating the conjugate of the complex vector.

(Fitch et al., 2002) proposes to compute the correla-

tion operation in the frequency domain by means of

the FFT by exploiting the correlation theorem in or-

der to achieve computational efﬁciency.

5 THE GC MEASURE

The GC measure, proposed in (Crouzil et al., 1996)

and derived from a measure introduced in (Scharstein,

1994), is based on two terms, referred to as distinc-

tiveness (D) and conﬁdence (C), both computed from

intensity gradients:

D(x, y) =

∑

i=1

∑

j=1

||G

(i, j) − G

(i, j)|| (21)

C(x, y) =

∑

i=1

∑

j=1



||G

(i, j)||+ ||G

(i, j)||



(22)

The GC measure is then deﬁned as:

GC(x, y) =

D(x, y)

C(x, y)

(23)

Its minimum value is 0, indicating the pattern is

identical to the image subwindow. For any other pos-

itive value, the greater the value, the higher the dis-

similarity between the two vectors. In order to com-

pute the partial derivatives, (Crouzil et al., 1996) pro-

poses to use either the Sobel operator or the Shen-

Castan ISEF ﬁlter (Shen and Castan, 1992). For ease

of comparison with other measures (i.e. G-SSD and

G-NCC) in our implementation we will use the for-

mulation based on the Sobel operator.

6 EXPERIMENTAL

COMPARISON

This section presents the experimental evaluation

aimed at assessing the performances of the various

measures presented in this paper. The 3 datasets,

available at: www.vision.deis.unibo.it/pm-eval.asp,

used for our experiments are characterized by a sig-

niﬁcant presence of the disturbance factors discussed

previously, and are now brieﬂy described.

Guitar. In this dataset, 7 patterns were extracted

from a picture which was taken with a good camera

sensor (3 MegaPixels) and under good illumination

conditions given by a lamp and some weak natural

light. All these patterns have to be sought in 10 im-

ages which were taken with a cheaper and more noisy

sensor (1.3 MegaPixels, mobile phone camera). Illu-

mination changes were introduced in the images by

means of variations of the rheostat of the lamp illumi-

nating the scene (G1 − G4), by using a torch light in-

stead of the lamp (G5− G6), by using the camera ﬂash

instead of the lamp (G7 − G8), by using the camera

ﬂash together with the lamp (G9), by switching off the

lamp (G10). Furthermore, additional distortions were

introduced by slightly changing the camera position

at each pose and by the JPEG compression.

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

476

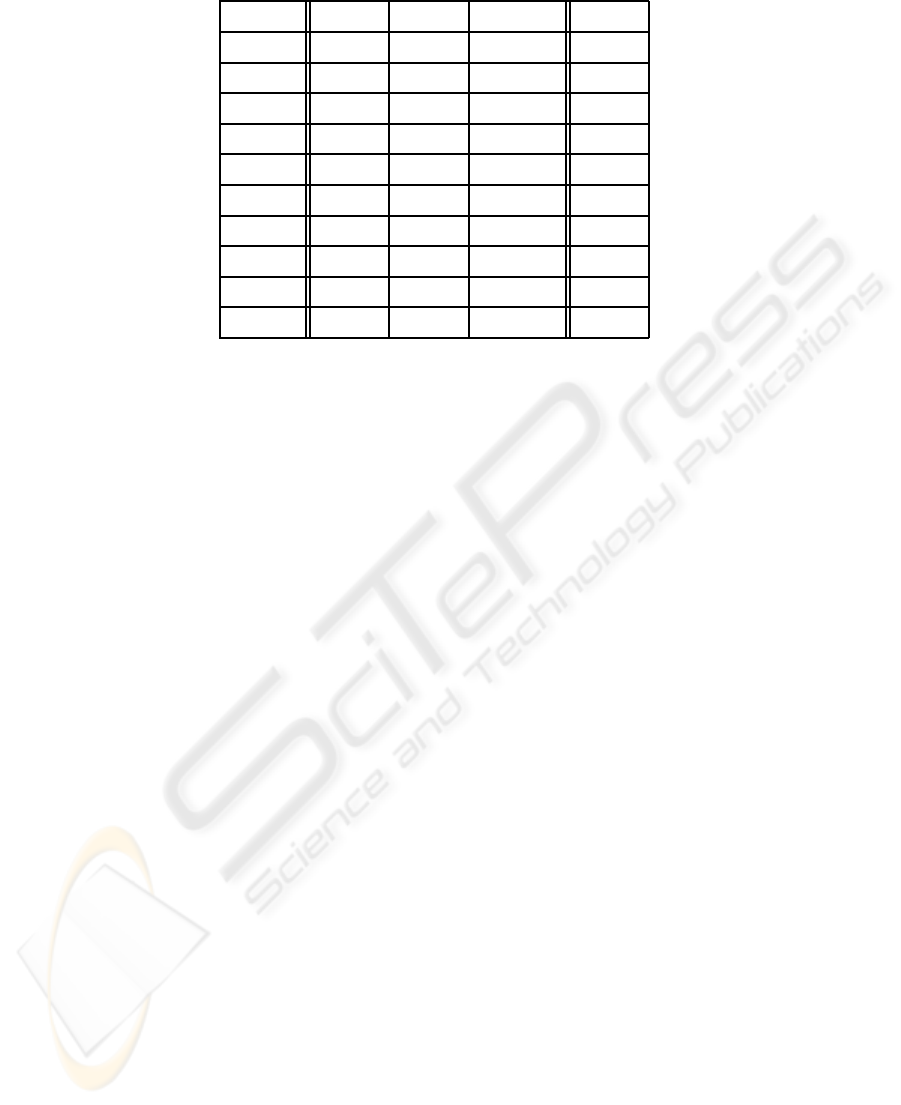
Table 1: Matching errors reported by the considered measures.

Guitar MP-IC MP-Occl Total

SSD 39 / 70 8 / 12 8 / 8 55 / 90

G-SSD 17 / 70 4 / 12 4 / 8 25 / 90

NCC 27 / 70 5 / 12 8 / 8 40 / 90

G-NCC 13 / 70 1 / 12 7 / 8 21 / 90

ZNCC 9 / 70 0 / 12 6 / 8 15 / 90

8 / 70 0 / 12 2 / 8 10 / 90

1,2

5 / 70 0 / 12 1 / 8 6 / 90

OC 13 / 70 1 / 12 1 / 8 15 / 90

GC 6 / 70 2 / 12 0 / 8 8 / 90

Mere Poulard - Illumination Changes. In dataset

Mere Poulard - Illumination Changes (MP-IC), the

picture on which the pattern was extracted was taken

under good illumination conditions given by neon

lights by means of a 1.3 MegaPixels mobile phone

camera sensor. This pattern is then searched within 12

images which were taken either with the same camera

(preﬁxed by GC) or with a cheaper, 0.3 VGA camera

sensor (preﬁxed by BC). Distortions are due to slight

changes in the camera point of view and by different

illumination conditions such as: neon lights switched

off and use of a very high exposure time (BC − N1,

BC − N2, GC − N), neon lights switched off (BC − NL,

GC − NL), presence of structured light given by a lamp

light partially occluded by various obstacles (BC−ST1,

··· , BC− ST5), neon lights switched off and use of the

camera ﬂash (GC − FL), neon lights switched off, use

of the camera ﬂash and of a very long exposure time

(GC − NFL). Also in this case, images are JPEG com-

pressed.

Mere Poulard - Occlusions. In the dataset Mere

Poulard - Occlusions (MP-Occl) the pattern is the

same as in dataset MP-IC, which now has to be found

in 8 images taken with a 0.3 VGA camera sensor. In

this case, partial occlusion of the pattern is the most

evident disturbance factor. Occlusions are generated

by a person standing in front of the camera (OP1, ··· ,

OP4), and by a book which increasingly covers part of

the pattern (OB1, ··· , OB4). Distortions due to illumi-

nation changes, camera pose variations, JPEG com-

pression are also present.

The number of pattern matching instances is thus

70 for the Guitar dataset, 12 for the MP-IC dataset and

8 for the MP-Occl dataset, for a total of 90 instances

overall. The result of a pattern matching process is

considered erroneous when the coordinates of the best

matching subwindow found by a certain measure are

further than ±5 pixel from the correct ones.

Tab. 1 reports the matching errors yielded by

the considered metrics on the 3 datasets. As it can

be seen, approaches speciﬁcally conceived to achieve

robustness generally outperform classical measures,

apart from the ZNCC which performs badly in pres-

ence of occlusions but shows good robustness in han-

dling strong photometric distortions. The two mea-

sures which yield the best performance are MF and

GC, with a number of total errorsrespectivelyequal to

6 and 8. In particular, MF performs better on datasets

characterized by strong photometric distortions, con-

versely GC seems to perform better in presence of oc-

clusions.

For what regards the 3 MF measures themselves,

it seems clear that the use of differences relative to

adjacent pixels suffers of the quantization noise intro-

duced by the camera sensor, hence they are less reli-

able than differences computed on a distance equal to

2. Moreover, as a consequence of the fact that MF

1,2

and MF

yield the same results on all datasets, MF

seems the more appropriate MF measure since it re-

quires only 2 correlation terms instead of the 4 needed

by MF

1,2

. Finally, for what regards traditional ap-

proaches, it is interesting to note that the application

of NCC and SSD on the gradient norms rather than on

the pixel intensities allows for a signiﬁcantly higher

robustness throughout all the considered datasets.

PERFORMANCE EVALUATION OF ROBUST MATCHING MEASURES

477

7 CONCLUSIONS AND FUTURE

WORKS

An experimental evaluation of robust matching mea-

sure for pattern matching has been presented. We

have compared traditional approaches with propos-

als speciﬁcally aimed at achieving robustness in pres-

ence of disturbance factors such as photometric dis-

tortions, noise, occlusions. The evaluation conducted

on a challenging dataset has pointed out that the best

performing metric is MF followedby GC, which were

able to achieve an error rate of respectively 6.7% and

8.9%. The experiments have also shown that a mod-

iﬁed version of the MF measure consisting of only

2 correlation terms instead of 4 allows for achieving

equivalent results with respect to the original formu-

lation introduced in (Tombari et al., 2007).

Future works aims at extending the proposedcom-

parison to other measures not speciﬁcally proposed

for the pattern matching problem, and also at enrich-

ing the dataset used for the evaluation with more im-

ages.

REFERENCES

Aschwanden, P. and Guggenbuhl, W. (1992). Experimental

results from a comparative study on correlation-type

registration algorithms. In Forstner, W. and Ruwiedel,

S., editors, Robust computer vision, pages 268–289.

Wichmann.

Bhat, D. and Nayar, S. (1998). Ordinal measures for image

correspondence. IEEE Trans. Pattern Recognition and

Machine Intelligence, 20(4):415–423.

Chambon, S. and Crouzil, A. (2003). Dense matching us-

ing correlation: new measures that are robust near oc-

clusions. In Proc. British Machine Vision Conference

(BMVC 2003), volume 1, pages 143–152.

Crouzil, A., Massip-Pailhes, L., and Castan, S. (1996). A

new correlation criterion based on gradient ﬁelds sim-

ilarity. In Proc. Int. Conf. Pattern Recognition (ICPR),

pages 632–636.

Fitch, A. J., Kadyrov, A., Christmas, W. J., and J, K. (2002).

Orientation correlation. In Rosin, P. and Marshall, D.,

editors, British Machine Vision Conference, volume 1,

pages 133–142.

Giachetti, S. (2000). Matching techniques to compute im-

age motion. Image and Vision Computing, 18:247260.

Kaneko, S., Satoh, Y., and Igarashi, S. (2003). Using selec-

tive correlation coefﬁcient for robust image registra-

tion. Journ. Pattern Recognition, 36(5):1165–1173.

Martin, J. and Crowley, J. (1995). Experimental compari-

son of correlation techniques. In Proc. Int. Conf. on

Intelligent Autonomous Systems, volume 4, pages 86–

93.

Scharstein, D. (1994). Matching images by comparing their

gradient ﬁelds. In Proc. Int. Conf. Pattern Recognition

(ICPR), volume 1, pages 572–575.

Seitz, P. (1989). Using local orientational information as

image primitive for robust object recognition. In Proc.

SPIE, Visual Communication and Image Processing

IV, volume 1199, pages 1630–1639.

Shen, J. and Castan, S. (1992). An optimal linear operator

for step edge detection. Graphical Models and Image

Processing (CVGIP), 54(2):112–133.

Tombari, F., Di Stefano, L., and Mattoccia, S. (2007). A ro-

bust measure for visual correspondence. In Proc. 14th

Int. Conf. on Image Analysis and Processing (ICIAP

2007), pages 376–381.

Ullah, F., Kaneko, S., and Igarashi, S. (2001). Orientation

code matching for robust object search. IEICE Trans.

Information and Systems, E-84-D(8):999–1006.

Zabih, R. and Woodﬁll, J. (1994). Non-parametric local

transforms for computing visual correspondence. In

Proc. European Conf. Computer Vision, pages 151–

158.

Zitov´a, B. and Flusser, J. (2003). Image registration

methods: a survey. Image and Vision Computing,

21(11):977–1000.

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

478