
COMPLETE AND STABLE PROJECTIVE HARMONIC
INVARIANTS FOR PLANAR CONTOURS RECOGNITION
Faten Chaieb and Faouzi Ghorbel
Ecole Nationale des Sciences de l’Informatique (ENSI), CRISTAL Laboratory, GRIFT
Campus Universitaire Manouba, 1015 Manouba, Tunisia
Keywords:
Projective invariance, descriptors, completeness, stability, planar contours, shape recognition.
Abstract:
Planar shapes recognition is an important problem in computer vision and pattern recognition. We deal with
planar shape contour views that differ by a general projective transformation. One method for solving such
problem is to use projective invariants. In this work, we propose a projective and parameterization invariant
generation framework based on the harmonic analysis theory. In fact, invariance to reparameterization is
obtained by a projective arc length curve reparameterization process. Then, a complete and stable set of
projective harmonic invariants is constructed from the Fourier coefficients computed on the reparameterized
contours. We experiment this set of descriptors on analytic contours in order to recognize projectively similar
ones.
1 INTRODUCTION
The recognition of planar shapes that are subjected
to certain viewing transformations has increasing in-
terest in many computer vision applications such as
robotic vision, data-base retrieval, registration and
three-dimensional (3D) reconstruction. Three dimen-
sional objects could be also considered as planar
when the camera is far away from the object and dis-
tances within the object are negligible. Planar shapes
are generally assumed to have a piecewise smooth
boundary that is represented by a bidimensional (2D)
continuous contour. When a contour undergoes rigid
motion and is then projected onto an image plane us-
ing a pinhole camera, the perspectively projected con-
tour image can be represented by a planar projective
transformation.
The use of projective-invariant approach to deal
with planar shape recognition problem in different
views seems to be the most efficient method mainly
when camera parameters or point-to-point correspon-
dences are unknown. In fact, a projective invariant
is a property of geometric configurations in one view
which remain unchanged under the projective trans-
formations (Mundy and Zisserman, 1992). In the pla-
nar case, projective transformations also called plane-
to-plane homographies have the structure of a group.
This group includes the well known Euclidean and
Affine groups.
Two main classes of planar projective invariants
have been studied: algebraic and differential invari-
ants. The algebraic invariants were applied to alge-
braic objects such as points, lines and conics. The
well known algebraic invariant is cross-ratio (Mundy
and Zisserman, 1992). Algebraic invariants are often
global and deal with the whole shape. However, it’s
generally hard to fit polynomials to complex shapes.
Differential invariants are applied to smooth curves.
They are based on local properties of shapes such as
derivatives however they require generally high order
derivatives (Weiss, 1992; Van Gool et al., 1992). Fur-
thermore, as the invariants are local, the local cor-
respondence between points of the images obtained
from different viewpoints should be known. Thus,
differential invariants cannot be applied directly and
needs other methods in order to solve their problems.
The semi-differential invariants has been introduced
to reduce the order of derivatives by adding reference
points (Brill et al., 1992; Van Gool et al., 1992). In ad-
dition, integral features approach integrates the local
invariants over the original arbitrary curve parameter
and provides global or integral invariants such as mo-
ments. Recently, a class of integral invariants with re-
spect to the Euclidean group are proposed in (Manay
et al., 2006). This set of invariants allows the analysis
of shapes at multiple scales.
Furthermore, Fourier analysis theory has provided
curves global invariants in the Euclidean case (Fourier
111
Chaieb F. and Ghorbel F. (2008).
COMPLETE AND STABLE PROJECTIVE HARMONIC INVARIANTS FOR PLANAR CONTOURS RECOGNITION.
In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 111-116
DOI: 10.5220/0001088301110116
Copyright
c
SciTePress

Descriptors) (Crimmins, 1982; Kunttu et al., 2004)
and affine case (Arbter et al., 1990). In (Kuthirummal
et al., 2004), the authors have proposed an algebraic
affine recognition constraint.
Although, differential invariants remain constant
in the case of projectivities, they still generally de-
pend on the curve parameterization. The parameter-
ization is chosen arbitrary and would not be neces-
sary the same for different views. Thus, we need to
deal with both parameterization and geometric trans-
formation invariance. Some works haveconsider such
problem and have proposed projective invariant de-
scriptors which are independent with respect parame-
terization (Weiss, 1992; Van Gool et al., 1992).
In this paper, we propose a projective and param-
eterization invariant generation framework based on
the harmonic analysis theory and differential geome-
try. In fact, we perform a projective curve reparam-
eterization with a projective arc length. Thus two
equiprojective reparameterized contours from two
different views are equivalent up to a starting point.
Then, a complete and stable set of projective har-
monic invariants is introduced by computing the C
3
-
Fourier coefficients on projective arc length reparam-
eterized contours.
The next section characterises the transformation
in the case of a projection by a pinhole camera. Then,
the equiprojective reparameterization process is intro-
duced. In section 4, we construct the complete and
stable set of projective invariants. Next, the NURBS
curve fitting is introduced. Section 6 presents some
experimental results.
2 GEOMETRIC
TRANSFORMATION AND
PERSPECTIVE PROJECTION
To characterize the geometric transformation between
two corresponding shape contours, we review the
concept of planar projective homography. Planar pro-
jective homography (also called projectivity) is a lin-
ear mapping in the planar projective space P
2
, H :
P
2
→ P
2
defined up to an arbitrary factor λ by a 3×3
matrix H.
The relation between corresponding views of
points on a world plane Π in a 3D space, can be
modeled by a planar homography induced by the
plane. Consider two views p and p
′
of a 3D space
point P ∈ Π, in two camera frames f and f
′
respec-
tively. We will denote their corresponding homoge-
neous coordinates by ep = (x, y, 1),
e
p
′
= (x
′
, y
′
, 1) and
e
P = (X,Y, 1). Let M = K[I|0] and M
′
= K
′
[R|t] be
the first and the second camera projection matrices
(respectively), where R and t are the relative rotation
and translation between the cameras and K and K
′
are the respective internal calibration matrices. Thus,
ep = K[I|0]
e
P and
e
p
′
= K
′
[R|t]
e
P.
Let n be the unit normal vector to the plane Π and
let d > 0 denote the distance of Π from the optical
center of the first camera. The linear transformation
from ep to
e
p
′
can be expressed as:
e
p
′
= K
′
(R+
1
d
tn
T
)K
−1
ep = Hep
3 G-INVARIANT
REPARAMETERIZATION
It was proven in differential geometry that a simple
curve is homeomorphic to the unit circle S
1
or the
real line R. Here, we consider only the first case
which corresponds to closed contours. Thus, planar
shapes are represented by their smooth boundaries as
a closed 2D continuous parametric curve. In homoge-
nous coordinates, a parameterization γ(t) of a planar
curve γ is an 1-periodic function of a continuous pa-
rameter t defined by:
γ : [0, 1] −→ R
3
t 7−→ γ(t) = [x(t), y(t), 1]
t
.
(1)
and noted by γ(t).
Throughout this section, we indicate with γ : S
1
→
R
2
a closed planar contour and G a group acting on
R
2
.
It’s well known that a same parametric curve may
have different parameterizations. The invariants com-
puted from two different parameterizations of the
same geometric curve are generally different. This
is due to parameterization dependence on transforma-
tions. One solution to this problem consists in per-
forming a G-invariant reparameterization of the curve
where G is the geometric transformations group.
Definition 3.1. A reparameterization of a curve γ,
noted (γ(
b
t)), is defined as follows:
γ(
˜
t) = γ(τ(t)) = [x(τ(t)), y(τ(t))]
t
, t ∈ [0, 1]. (2)
where τ is an increasing function defined on [0,1].
Definition 3.2. A G-invariant reparameterization is
the process of reparameterizing the curve by a G-
invariant arc length.
Let γ
1
(t
1
) and γ
2
(t
2
) two parameterizations of a
geometric curve and its image by a geometric trans-
formation g. After G-invariant reparameterization,
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
112

both curve parameterizations verify the following
equation :
γ
2
(
˜
t ) = g(γ
1
(
˜
t + t
0
)), t
0
∈ Z et g ∈ G, (3)
where t
0
is departure points difference between the
contours.
Here we study the case of planar projective trans-
formations. Many projective arc lengths have been
introduced in literature. The classical projective arc
length is defined by the following equation (Cartan,
1937).
σ(t) =
1
L
Z
t
0
3
p
|H(u)|du, t ∈ [0, 1] (4)
where
H(t) = −
1
3
pq+
2
27
p
3
−
1
2
q
′
+
1
3
pp
′
+
1
6
p
′′
,
p = −
det(γ
′′′
(t) γ
′
(t))
det(γ
′′
(t) γ
′
(t))
, q =
det(γ
′′′
(t) γ
′′
(t))
det(γ
′′
(t) γ
′
(t))
and L is the curve projective length given by:
L =
Z
1
0
3
p
|H(u)|du.
4 PROJECTIVE HARMONIC
INVARIANTS
Let two planar curves γ
1
and γ
2
projectively simi-
lar. After PGL(2)-invariant reparameterization, these
curves given by their homogenous coordinates verify
the following equation:
γ
2
(
˜
t) = Hγ
1
(
˜
t + t
0
), t
0
∈ Z, (5)
where H is the planar projective transformation ma-
trix and t
0
is the departure point difference between
the two curves. We recall that a parametric represen-
tation of a planar curve is an 1-periodic function of a
continuous parameter t. Thus, Fourier coefficients of
the two curve reparameterizations exist and they are
related by:
c
n
[γ
2
] = e
2iπnt
0
Hc
n
[γ
1
], ∀n ∈ N, (6)
where c
n
[γ
i
] are Fourier coefficients of γ
i
.
Thus, PGL(2)-invariant descriptors of a curve γ
could be constructed as follows :
I
1
k
0
= |∆
1
k
0
,k
2
,k
3
|, I
1
k
1
= |∆
1
k
1
,k
2
,k
3
|,
I
1
k
2
= |∆
1
k
2
,k
0
,k
1
|, I
1
k
3
= |∆
1
k
3
,k
0
,k
1
|,
for all k ∈ N\{k
0
, k
1
, k
2
, k
3
},
I
1
k
= ∆
k
2
−k
3
k,k
0
,k
1
∆
k
3
−k
k
0
,k
1
,k
2
∆
k−k
2
k
0
,k
1
,k
3
, (7)
where ∆
p
k,l,m
= det(c
k
[γ], c
l
[γ], c
m
[γ])
p
and
det(x
1
, x
2
, x
3
) denotes the determinant of a ma-
trix which consists of three column vectors x
1
, x
2
and
x
3
∈ R
3
.
4.1 Invariance
In this section we demonstrate the homography in-
variance of the proposed set of invariants. We
consider a parametric curve γ and its image γ
t
by
an homography transformation H. Let M(γ) =
[c
k
[C], c
l
[γ], c
m
[γ]] and M(γ
t
) = [c
k
[C
t
], c
l
[γ
t
], c
m
[γ
t
]]
respectively the matrices composed by the k
th
, l
th
and
m
th
fourier coefficient rows of γ and γ
t
.
Let ∆
p
k,l,m
(γ) = det(M(γ))
p
where det(.) is the de-
terminant operator. Thus,
∆
p
k,l,m
(γ
t
) = e
2inp(k+l+m)
|det(H)|
p
∆
p
k,l,m
(γ) (8)
The descriptor set of the transformed curve γ
t
is then
given by :
I
1
k
(γ
t
) = e
2in[(k
2
−k
3
)(k+k
0
+k
1
)+(k
3
−k)(k
0
+k
1
+k
2
)+···
(k− k
2
)(k
0
+ k
1
+ k
3
)]
= |det(H)|
(k
2
−k
3
+k
3
−k+k−k
2
)
I
1
k
(γ)
and
(k
2
− k
3
)(k+ k
0
+ k
1
) + (k
3
− k)(k
0
+ k
1
+ k
2
)+ · ··
(k− k
2
)(k
0
+ k
1
+ k
3
) = 0
k
2
− k
3
+ k
3
− k+ k − k
2
= 0
so I
1
k
(γ
t
) = I
1
k
(γ).
4.2 Completeness
This set of invariants is not complete. In order to en-
sure the completeness property, we propose to com-
plete it with the two following sets constructed rela-
tively to two other fixed indices of k
0
, denoted by k
4
and k
5
:
I
2
k
4
= |∆
1
k
4
,k
2
,k
3
|,
I
2
k
2
= |∆
1
k
2
,k
4
,k
1
|, I
2
k
3
= |∆
1
k
3
,k
4
,k
1
|,
for all k ∈ N\{k
4
, k
1
, k
2
, k
3
},
I
2
k
= ∆
k
2
−k
3
k,k
4
,k
1
∆
k
3
−k
k
4
,k
1
,k
2
|∆
k
3
−k
k
4
,k
1
,k
2
|
∆
k−k
2
k
4
,k
1
,k
3
|∆
k−k
2
k
4
,k
1
,k
3
|
, (9)
I
3
k
5
= |∆
1
k
5
,k
2
,k
3
|,
I
3
k
2
= |∆
1
k
2
,k
5
,k
1
|, I
2
k
3
= |∆
1
k
3
,k
5
,k
1
|,
for all k ∈ N\{k
5
, k
1
, k
2
, k
3
},
I
3
k
= ∆
k
2
−k
3
k,k
5
,k
1
∆
k
3
−k
k
5
,k
1
,k
2
|∆
k
3
−k
k
5
,k
1
,k
2
|
∆
k−k
2
k
5
,k
1
,k
3
|∆
k−k
2
k
5
,k
1
,k
3
|
, (10)
where ∆
p
k,l,m
= det(c
k
[γ], c
l
[γ], c
m
[γ])
p
and
det(x
1
, x
2
, x
3
) denotes the determinant of a ma-
trix which consists of three column vectors x
1
, x
2
and
x
3
∈ R
3
.
COMPLETE AND STABLE PROJECTIVE HARMONIC INVARIANTS FOR PLANAR CONTOURS RECOGNITION
113

The proof of the completeness property is as fol-
lows: We denote by:
θ
1
2
= Arg(∆
k
2
,k
0
,k
1
) θ
1
3
= Arg(∆
k
3
,k
0
,k
1
)
θ
2
2
= Arg(∆
k
2
,k
4
,k
1
) θ
2
3
= Arg(∆
k
3
,k
4
,k
1
)
θ
3
2
= Arg(∆
k
2
,k
5
,k
1
) θ
3
3
= Arg(∆
k
3
,k
4
,k
1
)
(11)
We obtain the following system of determinants :
∆
k,k
0
,k
1
= I
1
k
[I
1
k
2
]
k−k
3
k
3
−k
2
[I
1
k
3
]
k
2
−k
k
3
−k
2
e
(k−k
2
)θ
1
2
+(k
3
−k)θ
1
2
k
3
−k
2
∆
k,k
4
,k
1
= I
2
k
[I
2
k
2
]
k−k
3
k
3
−k
2
[I
2
k
3
]
k
2
−k
k
3
−k
2
e
(k−k
2
)θ
2
2
+(k
3
−k)θ
2
2
k
3
−k
2
∆
k,k
5
,k
1
= I
3
k
[I
3
k
2
]
k−k
3
k
3
−k
2
[I
3
k
3
]
k
2
−k
k
3
−k
2
e
(k−k
2
)θ
3
2
+(k
3
−k)θ
3
2
k
3
−k
2
(12)
Thus, we can reconstruct the Fourier coefficients
c
k
[C] once the value of the three determinants are
known. So, to determine c
k
[C], we have the equations
system :
The unique solution is given by :
c
k
[C] =
e
−iθ
4
k
0
I
4
k
0
det(E, c
k
0
[C], c
k
1
[C])
det(E, c
k
4
[C], c
k
1
[C])
det(E, c
k
5
[C], c
k
1
[C])
(13)
where
E =
∆
k,k
0
,k
1
∆
k,k
4
,k
1
∆
k,k
5
,k
1
(14)
and θ
4
k
0
= Arg(∆
k
0
,k
5
,k
1
).
4.3 Stability
The power values (k − k
2
) or (k
3
− k) could be nega-
tive so the invariant function becomes an hyperbolic
function which is not continuous. In order to solve
this problem, we propose to divide by the correspond-
ing complex modules. So, we obtain the following
stable invariant set :
I
1
k
0
= |∆
1
k
0
,k
2
,k
3
|, I
1
k
1
= |∆
1
k
1
,k
2
,k
3
|,
I
1
k
2
= |∆
1
k
2
,k
0
,k
1
|, I
1
k
3
= |∆
1
k
3
,k
0
,k
1
|,
for all k ∈ N\{k
0
, k
1
, k
2
, k
3
},
I
1
k
= ∆
k
2
−k
3
k,k
0
,k
1
∆
k
3
−k
k
0
,k
1
,k
2
|∆
k
3
−k
k
0
,k
1
,k
2
|
∆
k−k
2
k
0
,k
1
,k
3
|∆
k−k
2
k
0
,k
1
,k
3
|
, (15)
where ∆
p
k,l,m
= det(c
k
[C], c
l
[C], c
m
[C])
p
and
det(x
1
, x
2
, x
3
) denotes the determinant of a ma-
trix which consists of three column vectors x
1
, x
2
and
x
3
∈ R
3
.
Such development is not a rigorous proof of sta-
bility criterion. In future work, we will give a way to
establish the stability property.
5 CONTOUR FITTING WITH
NURBS
In image analysis, data is always discrete. So approx-
imation or interpolation methods are needed to get a
continuous representation of the studied object. In the
case of objects described by their external contours,
these methods are called curve algorithms. A curve
algorithm is invariant to a transformations group G if
and only if :
g.F(D) = F(g.D) ∀g ∈ G, ∀D ∈ D
n
. (16)
This means that applying a curve algorithm to the
image by a transformation g of a data set is equiv-
alent to the image of the curve algorithm applied to
the discrete data by the same transformation g. The
NURBS (Non-Uniform Rational BSplines) are curve
algorithms invariant to projective transformations.
In this work, we have used the optimal inter-
polation scheme proposed by (Gaffney and Powell,
1976) since it provides the center function in the band
formed by all interpolants to the given data that, in
addition, have their k
th
derivative between −M and M
(for large M).
6 EXPERIMENTAL RESULTS
In this section, we present some experiments that il-
lustrate the different steps needed to compute the pro-
posed set of projective invariants. First, we consider
two planar contours obtained up on a projective trans-
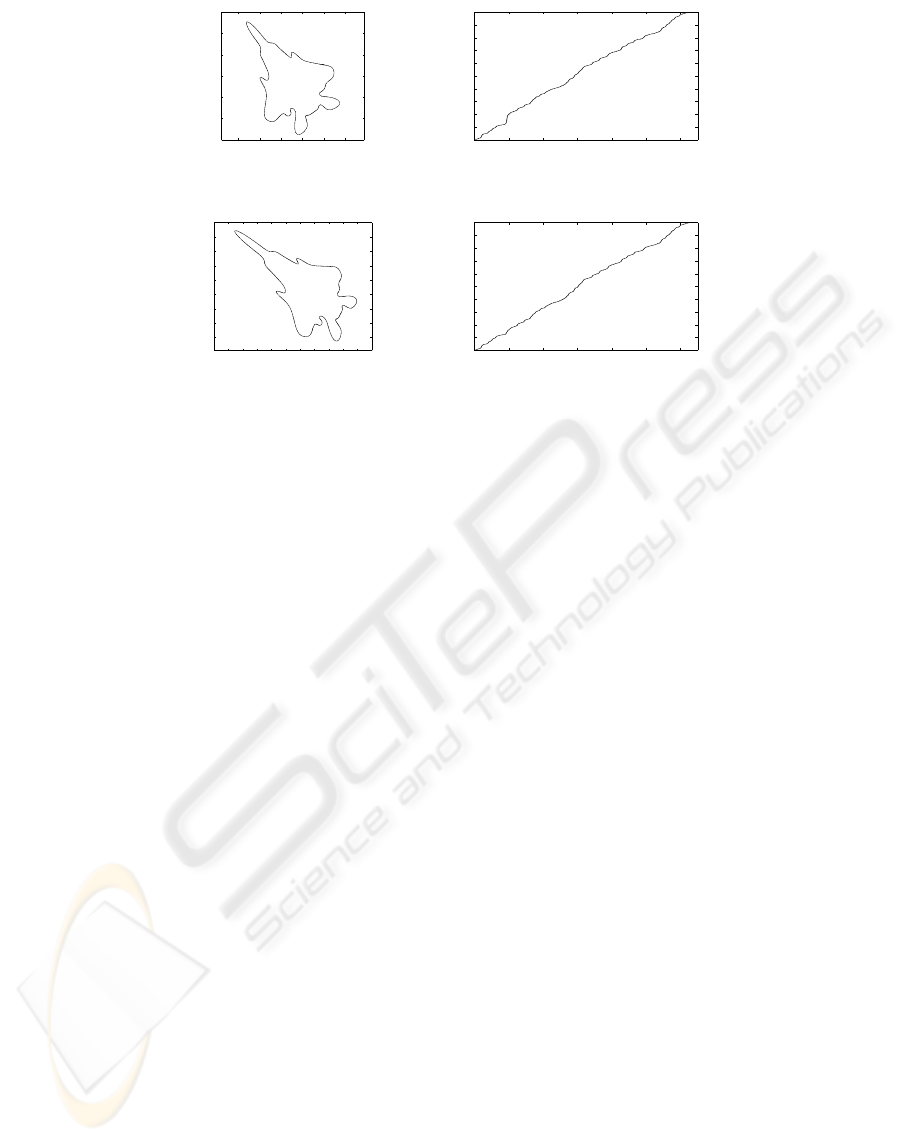
formation. Figures 1(a) and 1(c) show the projective
arc length parameterization of both contours. It’s im-
portant to notice that the obtained parameters of both
contours are upon a translation. The projective arc
lengths computed in the reparameterization step are
shown in figures 1(b) and 1(d). The performance of
the proposed descriptors set is evaluated using a set
of 204 analytic contours created by performing pla-
nar homographies on a set of six parametric contours
2(a). The planar homographies are obtained by vary-
ing intrinsic and extrinsic camera parameters.
Figures 2(b) and 2(c) show shape matching re-
sults. The distance used to compute similarity be-
tween two contours is the Euclidean one. We notice
that the contour cc− 1 is matched to 21 correct con-
tours. For the case of the contour cc− 4, 11 contours
are correctly matched. The matching errors are due
to approximations and the required high order deriva-
tives.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
114
20 40 60 80 100 120
0
20
40
60
80
100
120
(a)
0 1 2 3 4 5 6
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
(b)
−0.2 −0.1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1.1
(c)
0 1 2 3 4 5 6
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
(d)
Figure 1: Planar contours reparameterization results.
7 CONCLUSIONS
In this paper we proposed complete and stable pro-
jective invariant descriptors. This set of descriptors
is based on a projective arc length parameterization.
The invariance, completeness and stability of these
descriptors are theorically proved. Experimental re-
sults of contour reparameterization process are pre-
sented. Promising shape matching results are ob-
tained on a set of analytic planar closed contours. In
our future work, we intend to test these descriptors
on a set of planar contours extracted from grey-level
images. Furthermore, the robustness of the proposed
descriptors set to noise will be explored.
REFERENCES
Arbter, K., Snyder, W., Burkhardt, H., and Hirzinger, G.
(1990). Application of affine-invariant fourier descrip-
tors to recognition of 3-d objects. IEEE trans. on Pat-
tern Analysis and Machine Intelligence, 12(7):640–
647.
Brill, M. H., Barrett, E. B., and Payton, P. M. (1992). Pro-
jective invariants for curves in two and three dimen-
sions. In press, M., editor, Geometric Invariance in
Computer Vision, pages 193–214.
Cartan, E. (1937). La thorie des groupes finis et continus et
la gomtrie diffrentielle traite par la mthode du repre
mobile. Jacques Gabay, 1992.
Crimmins, T. (1982). A complete set of fourier descriptors
for two-dimensional shapes. SMC, 12:848–855.
Gaffney, P. W. and Powell, M. J. D. (1976). Numeri-
cal Analysis, volume 506 of Lecture Notes in Math-
ematics, chapter Optimal Interpolation, pages 90–99.
Springer.
Kunttu, I., Lepisto, L., Rauhamaa, J., and Visa, A. (2004).
Multiscale fourier descriptor for shape-based image
retrieval. Pattern Recognition, 2:765 – 768.
Kuthirummal, S., Jawahar, C., and Narayanan, P. (2004).
Fourier domain representation of planar curves for
recognitionin multiple views. Pattern Recognition,
37(4):739–754.
Manay, S., Cremers, D., Byung-WooHong, Jr., A. J. Y., and
Soatto, S. (2006). Integral invariants for shape match-
ing. IEEE Transactions on Pattern Analysis and Ma-
chine Intelligence, 28(10):1602–1618.
Mundy, J. L. and Zisserman, A., editors (1992). Geometric
invariance in computer vision. MIT Press.
Van Gool, L. J., Moons, T., Pauwels, E., and Oosterlinck, A.
(1992). Semi-differential invariants. In press, M., ed-
itor, Geometric Invariance in Computer Vision, pages
157–192.
Weiss, I. (1992). Noise resistant invariants curves. In Ge-
ometric Invariance in Computer Vision, pages 1135–
1156. MIT Press.
COMPLETE AND STABLE PROJECTIVE HARMONIC INVARIANTS FOR PLANAR CONTOURS RECOGNITION
115

(a)
(b)
(c)
Figure 2: (a) set of planar contours; (b) and (c) shape matching results of contour cc-1 and cc-4.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
116
