DETECTION OF FACES IN WIRE-FRAME POLYHEDRA

Interactive Modelling of Uniform Polyhedra

Hidetoshi Nonaka

Hokkaido University, N14W9, Sapporo, 060 0814, Japan

Keywords: Uniform polyhedron, polyhedral graph, simulated elasticity, interactive computing, recreational

mathematics.

Abstract: This paper presents an interactive modelling system of uniform polyhedra including regular polyhedra,

semi-regular polyhedra, and intersected concave polyhedra. In our system, user can virtually “make” and

“handle” them interactively. The coordinate of vertices are computed without the knowledge of faces, solids,

or metric information, but only with the isomorphic graph structure. After forming a wire-frame polyhedron,

the faces are detected semi-automatically through user-computer interaction. This system can be applied to

recreational mathematics, computer assisted education of the graph theory, and so on.

1 INTRODUCTION

This paper presents an interactive modelling system

of uniform polyhedra using simulated elasticity.

Uniform polyhedra include five regular polyhedra

(Platonic solids), thirteen semi-regular polyhedra

(Archimedean solids), and four regular concave

polyhedra (Kepler-Poinsot solids). Alan Holden is

describing in his writing, “The best way to learn

about these objects is to make them, next best to

handle them (Holden, 1971).” Traditionally, these

objects are made based on the shapes of faces or

solids. Development figures and a set of regular

polygons cut from card boards can be used to

assemble them. Kepler-Poinsot solids can be formed

by stellation of faces of “core” polyhedra.

“PolyFormes” is an application program for dialog-

based declarative modelling of polyhedra (Martin,

1999). These methods are based on faces. On the

other hand, some semi-regular polyhedra can be

formed by truncation of other solids. Kepler-Poinsot

solids can be also formed by faceting of solids of

“case” polyhedra. These methods are based on

solids (Coxeter, 1973).

In our system, user can virtually “make” and

“handle” all of the uniform polyhedra without the

knowledge of faces, solids, or metric information,

but only with the isomorphic graph structure. After

forming a wire-frame polyhedron with the vertices

and the edges, the faces are detected semi-

automatically through user-computer interaction.

2 UNIFORM POLYHEDRA

2.1 Platonic Solids

Five Platonic solids are listed in Table 1. The

symbol

P indicates that the number of faces

gathering around a vertex is n, and each face is m-

sided regular polygon.

Table 1: The list of Platonic solids.

Symbol Polyhedron Vertices Edges Faces

P Tetrahedron 4 6 4

P Cube 8 12 6

Octahedron 6 12 8

P Dodecahedron 20 30 12

P Icosahedron 12 30 20

Platonic solids, or regular solids, are convex

polyhedra with faces that are regular and congruent

polygons, while their vertices lie on the circum-

sphere, their vertex figures are also regular and

congruent.

2.2 Archimedean Solids

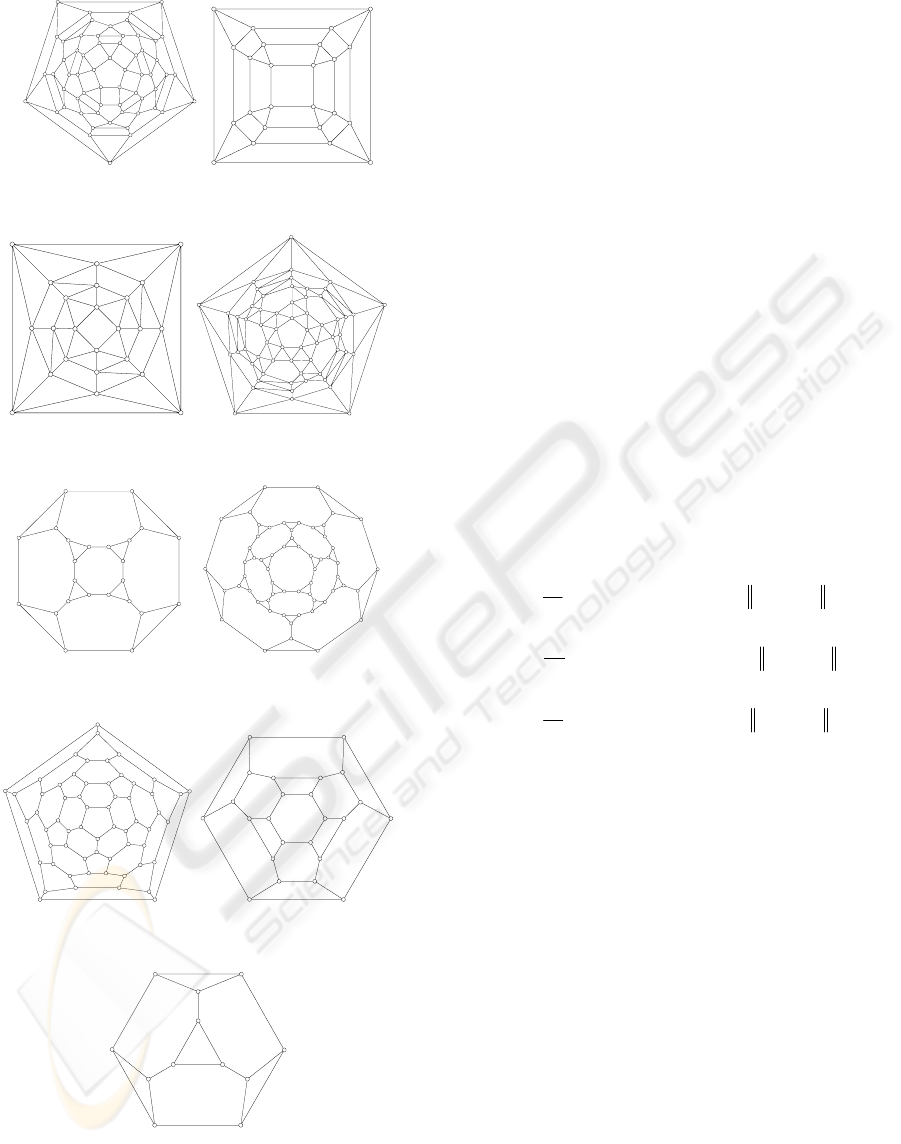
Thirteen Archimedean solids are shown in Figure 1.

Archimedean solids, or semi-regular solids, are

surrounded by several sorts of regular polygons, and

134

Nonaka H. (2008).

DETECTION OF FACES IN WIRE-FRAME POLYHEDRA - Interactive Modelling of Uniform Polyhedra.

In Proceedings of the Third International Conference on Computer Graphics Theory and Applications, pages 134-137

DOI: 10.5220/0001095301340137

 SciTePress

their vertex figures are not regular but congruent

polygons. Their vertices lie on the circum-sphere.

Some of Archimedean solids can be obtained by

truncation of other polyhedra.

2.3 Kepler-Poinsot Solids

Four Kepler-Poinsot solids are shown in Figure 2.

(5/2)

K (great stellated dodecahedron) and 5

(5/2)

(small stellated dodecahedron) are regular concave

polyhedra with pentagrams (5/2) as faces.

( a )

(3 4)

⋅

( b )

4610

⋅⋅

( c )

468

⋅⋅

( d )

(3 5)

⋅

( e )

3454

⋅⋅⋅

( f )

⋅

( g )

⋅

( h )

⋅

( i )

⋅

( j )

310

⋅

( k )

⋅

( l )

⋅

(m)

⋅

Figure 1: Thirteen Archimedean solids generated by the

system.

( a )

5/2

( b )

5/2

( c )

(5/2)

K ( d ) 5

(5/2)

Figure 2: Four Kepler-Poinsot solids generated by the

system.

3 POLYHEDRAL GRAPH

3.1 Polyhedral Graph

Drawing graph is the first step of polyhedron

modelling in the system. Polyhedral graphs

isomorphic to Archimedean solids are illustrated in

Figure 3-4. Kepler-Poinsot solids are isomorphic to

icosahedron or dodecahedron.

( a )

(3 4)

⋅

( b )

4610

⋅⋅

( c )

468

⋅⋅

( d )

(3 5)

⋅

Figure 3: Polyhedral graphs isomorphic to Archimedean

solids (1). (to be continued).

DETECTION OF FACES IN WIRE-FRAME POLYHEDRA - Interactive Modelling of Uniform Polyhedra

135

( e )

3454

⋅⋅⋅

( f )

⋅

( g )

⋅

( h )

⋅

( i )

⋅

( j )

310

⋅

( k )

⋅

( l )

⋅

(m)

⋅

Figure 4: Polyhedral graphs isomorphic to Archimedean

solids (2).

3.2 Simulated Elasticity

We define three binary relations between two

vertices:

The relation

adjacent corresponds to the length

of an edge in a 3 dimensional space. The relation

neighbour means that the length of path between

two vertices is 2, and two vertices are

neighbourhood of another vertex, and it corresponds

to the shape of vertex figure in a 3 dimensional

space. The relation

diameter corresponds to the

circum-sphere.

Virtual elastic forces are assumed between

vertices according to Hooke’s law and three

relations defined in the previous section. Let

and

LLL be natural length of virtual spring, and

each lower suffix indicates “adjacent”, “neighbour”,

or “diameter”. Let

and

kkk be spring constant,

which varies from 0 to 1. Bold-faced

,0, 1

ip=−v " stands for the 3 dimensional

coordinate of vertex

vV∈ . Then the total elastic

potential E

is given as follows:

tand

EEEE=++

(1)

()

(, )

aaij

i j adj acent v v

nnij

ijneighbourvv

ddij

ijdiametervv

<∧

⎧

⎪

=−−⎪

⎪

=−−

⎨

⎪

=−−

⎪

⎩

∑

4 DETECTION OF FACES

After constructing polyhedral graph, and arranging

vertices in 3-dimensional space using elastic

potential, the next step is detecting and selecting

faces. In the case of Platonic solids, Archimedean

solids, prisms, and anti-prisms, common routine is

available.

The faces of Kepler-Poinsot solid are detected

by separate routine. Selecting triangles from great

icosahedron is common with selecting triangles

from icosahedron. Selecting pentagrams from great

stellated dodecahedron is common with selecting

pentagons from dodecahedron. Lastly, selecting

pentagon from great dodecahedron is common with

selecting pentagram from small stellated

dodecahedron.

At this stage, the modelling of polyhedron is

completed. The final step is rendering the wire-

GRAPP 2008 - International Conference on Computer Graphics Theory and Applications

136

frame polyhedron with detected faces. In the case of

Kepler-Poinsot solids, faces are intersecting each

other. Then the process of hidden surface removal is

required. In the case of presented system, the target

machine is low cost PC with single CPU without

graphics accelerators. We tried to calculate the

geometric interference, and detected the exposed

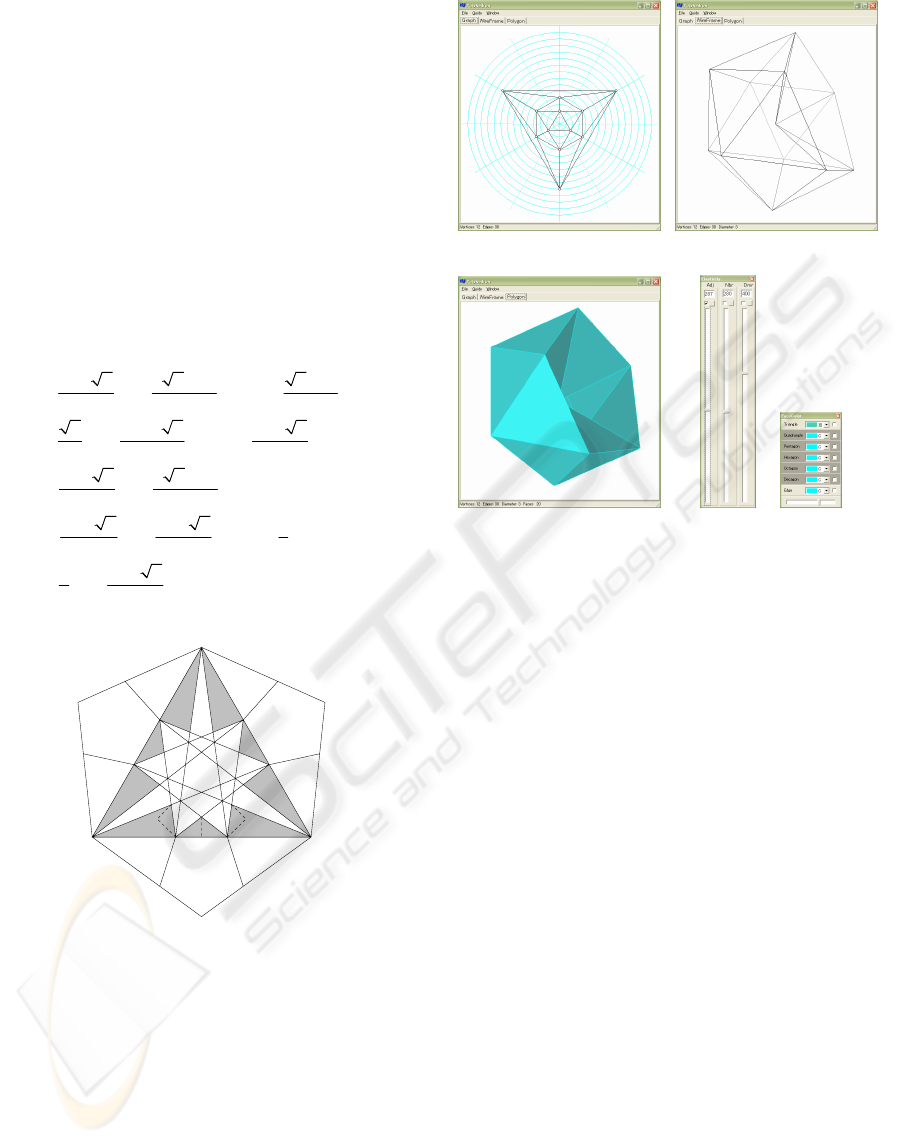
fragments. As an example, such fragments in a

triangle of great icosahedron are obtained as is

shown in Figure 5, where shaded region is outside of

great icosahedron.

Let

,,, ,abc r"

be the position vector of each

point in the figure:

,,,,OA OB OC OR

JJJG

JJG JJJG JJJG

, then they

are expressed by

a and b as follows,

55 355

510

−−

=+ca b

−

=da

5525

−

=+ea b

−

a ,

55 355

10 10

−−

=+ga b. (5)

35 35

+−

=+pab,

=qa

135

−

=+ra b (6)

Figure 5: Nine exposed fragments of triangle OAB∆

surrounding the great icosahedron.

5 SYSTEM OVERVIEW

Figure 6 shows snapshots of GUI. In this example,

depressed icosahedron is obtained. It means the

elastic potential remains at a local minimum. It can

be recovered interactively by pulling a proper vertex,

or increasing the natural length of diameter, and so

on.

( a ) Graph input window ( b ) Wire-frame window

( c ) Polygon window ( d ) Control tools

Figure 6: Snapshots of GUI of the system.

6 CONCLUSIONS

This paper proposed an interactive modelling system

of uniform polyhedra. Process of modelling is

composed of following three steps. Firstly, a

polyhedral graph is constructed by editing graph

with several graph operations. Secondly, wire-frame

polyhedron is formed by simulated elasticity with

the relation of adjacent, neighbour, and diameter.

Lastly, proper faces are detected semi-automatically

through user-computer interaction. This system can

be applied to recreational mathematics, computer

assisted education of the graph theory, and so on.

REFERENCES

Coxeter, H. S. M., 1973. Regular Polytopes, Dover

Publications, New York.

Coxeter, H. S. M., 1999. The Beauty of Geometry, Twelve

Essays, Dover Publications, New York.

Holden, A., 1971. Shapes, Space, and Symmetry,

Columbia University Press, New York.

Martin, P. and Martin, D., 1999. PolyFormes: Software

for the declarative modelling of polyhedra, The Visual

Computer, 15 (2), 55-76.

DETECTION OF FACES IN WIRE-FRAME POLYHEDRA - Interactive Modelling of Uniform Polyhedra

137