
OFF-LINE ROBUSTIFICATION OF EXPLICIT MPC LAWS
The Case of Polynomial Model Representation
Pedro Rodríguez-Ayerbe and Sorin Olaru
Department of Automatic Control, Supélec, 3 rue Joliot Curie, F91192 Gif-sur-Yvette, France
Keywords: Piecewise affine controller, Robustification, Youla-Kucera parameter, Model Predictive Control.
Abstract: The paper deals with the predictive control for linear systems subject to constraints, technique which leads
to nonlinear (piecewise affine) control laws. The main goal is to reduce the sensitivity of these schemes with
respect to the model uncertainties and avoid in the same time a fastidious on-line optimisation which may
reduce the range of application. In this idea a two stage predictive strategy is proposed, which synthesizes in
a first instant an analytical (continuous and piecewise linear) control law based on the nominal model and
secondly robustify the central controller (the controller obtained when no constraint is active). This
robustification is then expanded to all the space of the piecewise structure by means of its corresponding
noise model.
1 INTRODUCTION
The model predictive control (MPC) laws are
optimization based techniques which allow
constraints handling from the design stage. The
analytical formulation of the optimum and its on-line
evaluation avoids a challenging optimization from
the point of view of the real-time control
environment. Solutions in this direction exist at least
for two important classes of problems (linear and
quadratic) subject to linear constraints due to the
Abadie constraint qualification (Goodwin et al.,
2004). It must be said that these are in fact a part of
a larger class of multiparametric convex programs
(Bemporad et al., 2002b) for which exact or
approximate algorithms exist (TØndel et al., 2003,
Seron et al, 2003, Olaru and Dumur, 2004;
Bemporad and Filippi, 2006).
In the case of robust predictive control laws, the
model uncertainties and the disturbances can be
taken into account at the design stage. A popular
technique in this sense is the use of a min-max
criterium (in the case when the extreme combination
of disturbances or uncertainties are known)
(Kerrigan and Maciejowski, 2004; Bemporad et al.,
2002a) which comes finally to the resolution of a
single multiparametric linear program. The structure
of this ultimate optimization is however quite
complex and large prediction horizons cannot be
handled due to the exponential growth of
disturbances realization to be taken into account. In
a slightly different manner, by constructing an
estimation mechanism (Goodwin et al., 2004) for the
constrained variables, one can obtain alternatively a
robust control structure, but the multiparametric
optimization remains intricate.
A first study on the robustness improvements for
the explicit affine feedback policy constructed upon
constrained predictive control strategies was
presented in (Olaru and Rodriguez-Ayerbe, 2006).
The simplest way to proceed is to consider an
observer of the state variables (Goodwin et al.,
2004), the dimension of the state space being
preserved and the piece-wise structure of controller
unchanged. The same observer can be used for all
feasible regions and can be viewed as noise
characterisation of the model. Nevertheless, the
observer does not describe the entire class of
stabilizing controllers. The present paper presents an
improved result based on the Youla-Kučera
parametrization which spans the space of stabilizing
controllers. For a two-degree of freedom controller,
one has access to all the stabilizing controllers that
preserve the same input/output behavior, so the
Youla-Kučera parameter offers more degrees of
freedom than the use of an observer.
The robustification is made such that the state
space dimension of the controller is augmented. The
main contribution here is the reconstruction of the
noise model induced by the central Youla-Kučera
96
Rodríguez-Ayerbe P. and Olaru S. (2008).
OFF-LINE ROBUSTIFICATION OF EXPLICIT MPC LAWS - The Case of Polynomial Model Representation.
In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - SPSMC, pages 96-101
DOI: 10.5220/0001481300960101
Copyright
c
SciTePress

parameter, in order to use it to generate the
corresponding robust piece-wise controller.
In the following, section 2 briefly recalls the
predictive control and the Youla-Kučera
parametrization. Section 3 details the explicit
formulation of the control laws obtained in the
constrained case. Section 4 contains the main
contribution: the noise model of the Youla-Kučera
parameter and the numerical examples are presented
in section 5 and the final conclusions in section 6.
2 PREDICTIVE CONTROL
The Generalized Predictive Control (GPC) strategy,
introduced in (Clarke et al., 1987), uses for the
prediction a CARIMA plant model:
)(
)(
)()(
1
1
1
11
−
−
−
−−
Δ
+=
q
qC
uqByqA
t
tt
ξ
(1)
with u, y the input and output,
ξ
a white noise, A
and B polynomials in the backward shift operator of
degrees
a
n and
b
n respectively, and
11
1)(
−−
−=Δ qq the difference operator. The C
polynomial is the model argument taking into
account the noise influence on the system. In the
GPC case the cost function to be minimized over a
receding horizon is quadratic:
[][]
∑∑
=
−+
=
++
Δ+−=
u
N
j
jtj
N
Nj
jtjt
uywJ
1
2
1
2
2
1
ˆ
λ
(2)
where
21
, NN are the costing horizons,
u
N the
control horizon,
j
λ
the control weighting factor and
w the set-point.
Using the model (1) and the solution of some
Diophantine equations (Clarke et al., 1987), this
control strategy leads to two-degrees of freedom
RST controller, implemented through a difference
equation (Figure 1):
)(
1
1−
qA
)(tu
)(tw
)(
1
1−
Δ qS
)(
1−
qR
)(ty
)(td
)(
11 −−
qBq
)(qT
Figure 1: Two-degrees of freedom GPC controller.
In (Yoon and Clarke, 1995) the relation between
the RST controller obtained with C=1 and
1≠C is
studied. Considering
TSR
′′′
,, the controller
obtained with C=1 and
TSR ,, whose obtained with
1≠C , the following relations are obtained:
CTTBMqCSSMACRR
′
=−
′
=Δ+
′
=
−1
(3)
with:
∑
=
−
−
′
=
2
1
)()(
1
N
Ni
ii
i
i
EECqqM
α
(4)
[]
21 NN
α
α
K=m
(5)
m being the first row of
T1T
)( GΛGG
−
+ .
The set of all stabilizing controllers for the system
shown in Figure 1 is given by the Youla-Kučera
parametrization as follows (Maciejowski, 1989):
⎪
⎩
⎪
⎨
⎧
′
=
−
′
=
Δ+
′
=
=
−
den
numden
numden
den
num
QTT
BQqQSS
AQQRR
Q
Q
Q
1
(6)
where )(
1−
qQ is a stable transfer function.
The choice of the Q parameter is a complex
problem on its own but it is not the subject of the
current paper. The methods presented in (Rodriguez
and Dumur, 2005; Rossiter 2003; Ansay et al., 1998;
Yoon and Clarke, 1995; Kouvaritakis et al., 1992)
can be used for the choice of this parameter.
Comparing (3) and (6) it turns out that the
controller for
1≠C is obtained for Q=M/C. As M
depends of C as shown by (4), the robustification by
the C polynomial has less degrees of freedom than
the robustification by Youla-Kučera parameter
(Yoon and Clarke, 1995).
3 EXPLICIT CONSTRAINED
GPC LAWS
In the case when the GPC law is subject to
constraints, the optimization has to be solved with
respect to a feasible domain. If the considered
constraints are stated on the control action, on the
control increment, on the plant outputs or any other
signal related by a CARIMA model to the control
signal, then one can restate them in a form
depending only on the control increment, leading to
a set of linear constraints (Ehrlinger et al., 1996):
OFF-LINE ROBUSTIFICATION OF EXPLICIT MPC LAWS - The Case of Polynomial Model Representation
97
⎩
⎨
⎧
+=
+≤
eqtequeq
intinuin
bpBkA
bpBkA
(7)
involving the optimization argument )(t
u
k and the
vector of context parameters:
{}
[]
TTT
T
wΔuγyp
pastpastpastt
=
(8)
which regroups a finite sequence of past inputs
Δu
,
future setpoints
w
, past outputs y and present and
future values of the signals under constraints (noted
for short
past
γ
).
It is interesting to observe that this set of
constraints characterizes in fact a parameterized
polyhedron (Olaru and Dumur, 2004) in the
optimization argument space. The optimum will lie
on a combination of its parameterized vertices and
thus one can construct the explicit solution for the
multiparametric optimization:
The use of a dual representation of the feasible
domain and projection mechanisms (see Olaru and
Dumur, 2004 and 2005) can be advantageous in
order to express the optimality conditions if there
exist unbounded feasible directions.
⎩
⎨
⎧
+=
+≤
eqtequeq
intinuin
t
t
t
J
u
bpBkA
bpBkA
k
)(
)(
:tosubject
min
)(
(9)
Subsequently, the predictive control law can be
described explicitly upon the solution of (9) as a
piecewise affine function of the vector of parameters
(Seron et al, 2003; Bemporad et al., 2002; Olaru and
Dumur, 2004).
itliLinu
CRKK
i
∈+= pppk for)(
*
(10)
with CR
i
, critical regions in the space of context
parameters, The GPC subjet to constraints has a
piecewise RST polynomial form:
ipastitititi
tlVwqTyqRuqS +++−=Δ
−−
γ
)()()(
11
(11)
for
{}
[]
ipastpastpast
CR∈
TTT
T
wΔuγy
.
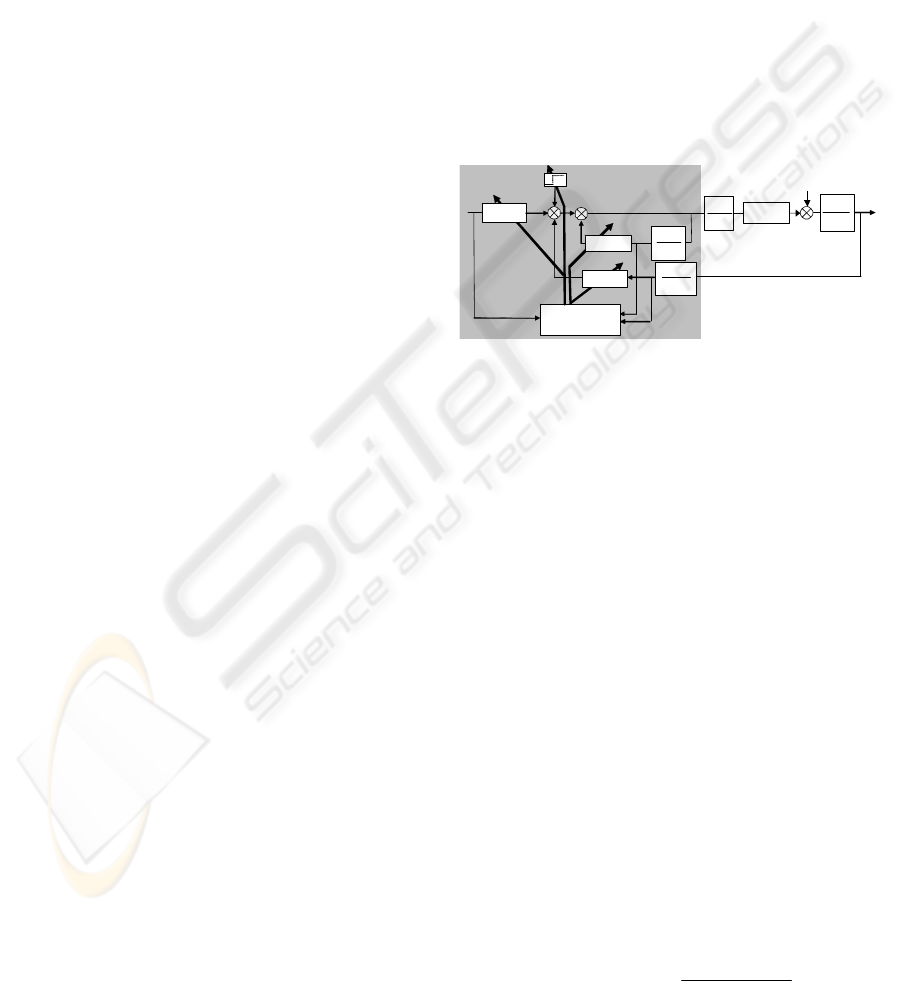
The structure of such a piecewise controller is
shown in Figure 2. Once the look-up table of local
polynomial RST laws is available, an efficient
positioning mechanism (based on a search tree) can
be constructed such that the on-line evaluation
routine can find the optimal control action according
to the GPC philosophy (TØndel et al., 2003).
4 ROBUSTIFICATION
At this stage, it is assumed that the design of initial
controller has been performed with
1
N ,
2
N ,
u
N ,
λ
adjusted to satisfy the required input/output
behavior. The resulting picewise two-degrees of
freedom RST controller will be denoted
iii
TSR
′′′
,, , in
the following sections.
The observer based robustification corresponds
to the consideration of an observer of the state. In
the case of GPC, this corresponds to a choice of a C
polynomial. The roots of this polynomial correspond
to the poles of the observer. The obtained piecewise
controller can be implemented as in Figure 2, see
also (Olaru and Rodriguez-Ayerbe, 2006, Camacho
and Bordons, 2004 ; Bitmead et al.,1990).
R
obustified piecew is
e
R
ST controller
w
-
Positioning
mechanism
)
(
1
1
−
q
C
-
)(
1
−
q
R
i
ipasti
tlV +
γ
+
)(
1
1
−
q
C
+
+
y
f
Δu
f
Δu
)(
1
1
−
q
Δ
T
i
(q)
y
)(
11
−
−
q
B
q
)(
1
1−
q
A
+
+
ξ
)(
1−
− qCS
i
Figure 2: Piecewise RST formulation for the GPC law
under constraints and robustification using the C
polynomial.
The Youla-Kučera parameter based robusti-
fication has more degrees of freedom than the use of
an observer. It allows to access the entire space of
stabilizing controllers. The idea is thus to robustify
the central RST law of the piecewise controller, that
is, the law where the constraints are not activated,
and to expand this robustification to the others RST
laws of the initial piecewise controller. The choice
of this parameter can be done using stability
robustness and nominal performance specifications,
see (Rodriguez and Dumur, 2005; Rossiter 2003;
Ansay et al., 1998; Yoon and Clarke, 1995;
Kouvaritakis et al., 1992). In the following the
selection will be done according to these principles.
As the use of an observer corresponds to the
consideration of a C polynomial for the noise
influence on the CARIMA model (1), the idea is to
find the corresponding noise model of the Youla-
Kučera parameter. To do this, an extra polynomial is
added in the model of the system. A
)(
1−
qD
polynomial will appear as following:
)()(
)(
)()(
11
1
1
11
−−
−
−
−−
Δ
+=
qqD
qC
uqByqA
t
tt
ξ
(12)
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
98

With this new model, Diophantine equations are:
)()()()()()(
)()()()()()(
111111
111111
−−−−−−−
−−−−−−−
=+
=+Δ
qDqEqBqHqqCqG
qCqFqqEqDqAq
jj
j
j
j
j
j
(13)
Finding the relation between the controller
obtained for C=D=1 and the one obtained for
1≠C
and
1≠D , we obtain something similar to (3).
Considering
TSR
′′′
,, the controller obtained with
C=D=1 and
TSR
~
,
~
,
~
whose obtained with 1≠C and
1≠D
, the following relations are obtained:
CTTMBqCSSMACRR
′
=−
′
=Δ+
′
=
−
~
~
~
~
~
1
(14)
With, (see Appendix for structural details) :
∑
=
−
−
′
=
2
1
)
~
()(
~
1
N
Ni
ii
i
i
DEECqqM
α
(15)
So, the D polynomial corresponding to the
considered Youla-Kučera parameter must verify:
∑
=
−−
−
′
==
2
1
)
~
()(
~
)(
11
N
Ni
ii
i
inum
DEECqqMqQ
α
(16)
Once the corresponding noise model has been
obtained, it can be used to regenerate the piecewise
affine controller. The same input/output behaviour
as for the initial one is assured, in the ideal case of
no model errors. A modified close loop behaviour
will be observed with respect to disturbance
rejection, robustness, etc.
The resolution of (16) is a non linear problem
that can be undertaken with standard optimization
methods. Nevertheless, is not always possible to
guarantee a real solution. The resolution of (16) and
its limitations are raising interesting questions,
research being currently conducted on this subject.
From a practical point of view, any such limit case
can be avoided by retuning the initial predictive
control parameters or the robustification
specification.
5 EXAMPLE
Consider the position control of an induction motor,
with 1.0724 ms as sampling period
)998.01)(1(
)8206.0821.0(10
)(
)(
)(
11
214
1
ref
1
1
−−
−−−
−
−
−
−−
+
==
qq
qq
q
q
qH
τ
θ
(17)
Constraints in control amplitude are considered:
],[
maxmaxref
τ
τ
τ
−∈ and 8.1
max
=
τ
. An initial
GPC controller is designed with
1== DC with the
following tuning parameters:
,1
1
=N ,16
2
=N
0001.0=
λ
and 2=
u
N . The position of the motor
is obtained through an encoder of 14400 points per
rotation, and the highs dynamics of the system
(current loop, inverter dynamic, mechanic dynamics
in high frequency) have been not identified.
This initial controller is obtained with (9). A
piecewise linear controller with 9 regions is
obtained. The central region corresponds to the case
where no constraint is active. This controller will be
noted
000
,, TSR .
To robustify off-line this piecewise controller,
the idea is to robustify the central one (
000
,, TSR )
and expand this robustification to other regions. In
this way a Youla-Kučera parameter has been
obtained by method described in (Rodriguez and
Dumur, 2005). The following parameter is
considered.
4321
321
7.0973.2838.4565.31
93.254117.890299.104992.4196
−−−−
−−−
+−+−
+++−
=
qqqq
qqq
Q
(18)
With (6), we obtain the controller
QQQ
TSR
000
,, .
Solving (16) with
den
QC = , the following D
polynomial is obtained:
4321
426.0018.0472.0873.01
−−−−
+−+−= qqqqD
(19)
This value has been obtained by available
optimization methods (classical Matlab routines in
occurrence) as long as (16) represents a set of non
linear equations difficult to solve analytically.
With this D polynomial, the optimization
problem (9) can be solved but this time with
matrices obtained from (13) for
den
QC = and D as
in (19). The solution of this new optimization
problem leads to a new piecewise controller with 9
regions, as the initial one. The central controller of
this piecewise controller correspond to
QQQ
TSR
000
,, .
Figures 3 and 4 show the obtained simulations
results for a filtered step reference considering a
second order neglected dynamic in high frequency
of the following characteristics:
srad /1000
0
=
ω
3.0=
ξ
.
In these figures we can observe that the obtained
behaviour is stable in the case of robustified
controller and instable in the case of initial
controller. So, the robustified controller has better
OFF-LINE ROBUSTIFICATION OF EXPLICIT MPC LAWS - The Case of Polynomial Model Representation
99

behaviour towards uncertainties in high frequency
and the continuity between regions is guaranteed.
0 0.2 0.4 0.6 0.8 1 1.2 1.4
0
0.5
1
Pos. Ref.
(rad)
0 0.5 1 1.5
-0.2
0
0.2
Pos. Error
(rad)
0 0.5 1 1.5
-2
0
2
Control
signal
0 0.5 1 1.5
0
5
10
Active
Region
time (s)
Figure 3: Position reference, position error, control signal
and active region for the initial controller and uncertain
model.
0 0.2 0.4 0.6 0.8 1 1.2 1.4
0
0.5
1
Pos. Ref.
(rad)
0 0.5 1 1.5
-0.2
0
0.2
Pos. Error
(rad)
0 0.5 1 1.5
-2
0
2
Control
signal
0 0.5 1 1.5
0
5
10
Active
Region
time (s)
Figure 4: Position reference, position error, control signal
and active region for the robustified controller and
uncertain model.
6 CONCLUSIONS
The paper investigated the robustification methods
for the control laws obtained in a constrained
predictive control framework. The idea is to design
in a first instance a piecewise polynomial controller
which satisfy the basic demands in terms of tracking
performances. In a second stage, the same predictive
control structure (prediction horizon, weightings,
etc.) is robustified using the model arguments
accounting for the noise influence. The idea is
similar to that of using a fixed observer, but
exploring all the class of stabilizing controllers of
the unconstrained system. This increases the number
of degrees of freedom.
The robustification of initial unconstrained
controller is made using the Youla-Kučera
parametrization, and then this robustification is
expanded to all the piecewise structure of the
controller. For this, the noise model corresponding
to the Youla-Kučera parameter is found, and use to
regenerate the robust piecewise controller by
preserving the same input/output behavior but being
more robust.
The limitations of the method are in the existence
of the corresponding noise model of the Youla-
Kučera parameter. This is transparent in the
resolution of a non linear equation system. The
robustification being done off-line, any infeasibility
can be handled by retuning the GPC parameters.
REFERENCES
Ansay P., M. Gevers and V. Wertz (1998). Enhancing the
robustness of GPC via a simple choice of the Youla
parameter. European Journal of Control, 4, 64-70.
Bemporad A., C. Filippi (2006). An Algorithm for
Approximate Multiparametric Convex Programming.
Computational Optimization and Applications, 35, 87-
108.
Bemporad A., F. Borelli and M. Morari (2002a). Model
predictive control based on linear programming: The
explicit solution. IEEE Transactions on Automatic
Control, 47, 1974–1985.
Bemporad A., M. Morari, V. Dua and E. Pistikopoulos
(2002b). The explicit linear quadratic regulator for
constrained systems. Automatica, 38, 3–20.
Bitmead R.R., M. Gervers and V. Wertz (1990).
Adaptative optimal control. The thinking Man’s GPC.
Prentice Hall. Englewood Cliffs, N.J.
Camacho E.F., C. Bordons, “Model predictive control”,
Springer-Verlag, London, 2nd ed., 2004.
Clarke D. W., C. Mohtadi and P.S. Tuffs (1987).
Generalized predictive control – Part I and II.
Automatica, 23(2), 137-160.
Clarke D.W. and R. Scattolini (1991). Constrained
receding-horizon predictive control. IEE Proceedings-
D, 138(4).
Ehrlinger A., P. Boucher and D. Dumur (1996). Unified
Approach of Equality and Inequality Constraints in
G.P.C. 5th IEEE Conference on Control Applications.
Goodwin, G.C., M.M. Seron, J.A. De Dona (2004).
Constrained Control and Estimation, Springer-Verlag,
London.
Kerrigan E. and J.M. Maciejowski (2004). Feedback min-
max model predictive control using a single linear
program: robust stability and the explicit solution.
International Journal of Robust and Nonlinear
Control, 14, 395-413.
Kouvaritakis B, J.A. Rossiter and A.O.T. Chang (1992).
Stable generalized predictive control: an algorithm
with guaranteed stability. IEE Proceedings-D, 139(4),
349-362.
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
100

Maciejowski J.M. (1989). Multivariable feedback design,
Addison-Wesley, England.
Olaru S. and D. Dumur (2004). A parameterized
polyhedra approach for explicit constrained predictive
control. 43rd IEEE Conference on Decision and
Control, The Bahamas.
Olaru S. and D. Dumur (2005). Avoiding constraints
redundancy in predictive control optimization
routines. IEEE Transactions on Automatic Control,
50(9), 1459–1466.
Olaru S., P. Rodriguez-Ayerbe (2006). Robustification of
explicit predictive control laws. 45rd IEEE
Conference on Decision and Control, San Diego.
Rodríguez P. and D. Dumur (2005), Generalized
Predictive Control Robustification Under Frequency
and Time-Domain Constraints. IEEE Transactions on
Control Systems Technology, 13(4), 577-587.
Rossiter J.A. (2003). Model Based Predictive Control. A
practical approach. CRC Press. Florida, USA.
Seron M., G. Goodwin, and J. D. Dona (2003).
Characterisation of receding horizon control for
constrained linear systems. Asian Journal of Control,
5(2), 271–286.
TØndel P., T. Johansen and A. Bemporad (2003).
Evaluation of piecewise affine control via binary
search tree. Automatica, 39 (5),945-950.
Yoon T.W. and D.W. Clarke (1995). Observer design in
receiding-horizon predictive control. Int. Journal of
Control, 61(1), 171-191.
APPENDIX
By solving the first Diophantine equation of (13) for
C=D=1 and
1≠C , 1≠D , a relationship between
the
R
′
polynomial obtained for C=D=1 and the R
~
obtained for
1≠C ,
1≠D
is obtained:
⎪
⎩
⎪
⎨
⎧
=+Δ
=
′
+
′
Δ
−−−−−−−
−−−−−
)()(
~
)(
~
)()()(
1)()()()(
111111
1111
qCqFqqEqDqAq
qFqqEqAq
j
j
j
j
j
j
)
~
(
~
jj
j
jj
EDECAqFCF −
′
Δ+
′
=⇒
R is obtained as:
∑
=
=
2
1
N
Ni
ii
FR
α
(see Yoon and
Clarke 1995).
For
R
~
:
MARC
EDECqARC
EDECAqFCFR
N
Ni
ii
i
i
N
Ni
ii
i
ii
N
Ni
ii
Δ+
′
=
−
′
Δ+
′
=
−
′
Δ+
′
==
∑
∑∑
=
==
2
1
2
1
2
1
)
~
(
))
~
((
~~
α
αα
With the same development, the corresponding
expression for
S
~
of (14) is obtained. Solving (16)
comes to the identification of a D polynomial
corresponding to
)(
1−
qQ
num
. It must be noted that
the first i coefficients of
1+i
E are the same than
those of
i
E polynomials. (
i
E is a polynomial of
degree i-1.) With this, the solution of D for the
numerical example has been obtained solving the
following non linear equations:
3
3
2
2
1
10
15
15
1
1
15
15
1
1
4
4
3
3
2
2
1
1
4
4
3
3
2
2
1
1
~~
1
~
1
1
1
−−−
−−
−−
−−−−
−−−−
+++=
+++=
′
++
′
+=
′
++++=
++++=
qmqmqmmM
qeqeE
qeqeE
qcqcqcqcC
qdqdqdqdD
K
K
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎝
⎛
−
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎝
⎛
⎪
⎪
⎭
⎪
⎪
⎬
⎫
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎝
⎛
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎝
⎛
⎪
⎪
⎩
⎪
⎪
⎨
⎧
−
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎝
⎛
′
′
′
′
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎝
⎛
~
1000
~
00
~
10
~~
1
000
00
0
1000
00
10
'1
000
00
0
3
2
1
0
16
1
12
13
14
151
4
43
432
4321
12
13
14
151
4
43
432
4321
M
M
L
O
L
L
L
O
L
L
m
m
m
m
e
e
e
ee
d
dd
ddd
dddd
e
e
e
ee
c
cc
ccc
cccc
α
α
(20)
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎛
=
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎛
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎛
−
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎛
′
′
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎛
0
0
~
~
1
100
01
00
1
1
01
0001
1
100
01
00
1
1
01
0001
15
1
1234
34
1234
123
12
1
15
1
1234
34
1234
123
12
1
M
M
M
M
M
M
M
L
MM
MOL
O
OO
O
M
L
M
M
L
MM
MOL
O
OO
O
M
L
e
e
dddd
dd
dddd
ddd
dd
d
e
e
cccc
cc
cccc
ccc
cc
c
(21)
With
)
~
~
(
1514321
eedddd L=x , the
following problem has been solved:
0)( =xF
With F defined by the matrix relations (20) and
(21), and using a standard optimization routine.
OFF-LINE ROBUSTIFICATION OF EXPLICIT MPC LAWS - The Case of Polynomial Model Representation
101
