
FEEDING A GENETIC ALGORITHM WITH AN ANT COLONY
FOR CONSTRAINED OPTIMIZATION
An Application to the Unit Commitment Problem
Guillaume Sandou, Stéphane Font, Sihem Tebbani
Supelec Automatic Control Department, 3 rue Joliot Curie, 91192 Gif-sur-Yvette, France
Arnaud Hiret, Christian Mondon
EDF Recherche et Développement, 6 quai Watier, 78401 Chatou, France
Keywords: Metaheuristics, unit commitment, ant colony, genetic algorithm, feasibility.
Abstract: In this paper, a new optimisation strategy for the solution of the classical Unit Commitment problem is
proposed. This problem is known to be an often large scale, mixed integer programming problem. Due to
high combinatorial complexity, the exact solution is often intractable. Thus, a metaheuristic based method
has to be used to compute a very often suitable solution. The main idea of the approach is to use ant colony
algorithm, to explicitly deal with the feasibility of the solution, and to feed a genetic algorithm whose goal
is to intensively explore the search space. Finally, results show that the proposed method leads to the
tractable computation of satisfying solutions for the Unit Commitment problem.
1 INTRODUCTION
The Unit Commitment problem is a classical
optimization mixed integer problem, referring to the
optimal scheduling computation of several
production units while satisfying consumer’s
demand. Due to temporal coupling of constraints
(time up and time down constraints), a long temporal
horizon is required, implying a large number of
binary variables. Numerous methods have already
been applied to tackle the difficulties of the problem
(Sen and Kothari, 1998). Roughly speaking, the
following classification can be made: Exact methods
(exhaustive enumeration, “Branch and Bound”
(Chan and Wang, 1993), dynamic programming
(Ouyang and Shahidehpour, 1991)); deterministic
approximated methods (priority lists (Senjyu, et al.,
2004)); Lagrangian relaxation (Zhai and Guan,
2002); Stochastic methods, also called
metaheuristics (simulated annealing (Yin Wa Wong,
1998), tabu search (Rajan and Mohan, 2004),
genetic algorithms (Swarup and Yamashiro, 2002)).
All these approaches have pros and cons: exact
methods suffer from combinatorial complexity,
deterministic approaches are very easy and tractable,
but can be strongly suboptimal, Lagrangian
relaxation allows taking into account constraints and
can be used to medium scale cases, but, due to the
non convexity of the objective function, no
guarantee can be given on the actual optimality. In
the case of metaheuristics methods, there is no
guarantee on the actual optimality of the solution,
but one can very often compute a very satisfying
suboptimal with low computation times. This kind
of methods is very interesting, especially for large
scale cases. However, one of the problems of such
stochastic methods is the management of the
feasibility of solutions. As the algorithm “walks”
randomly in the search space, there is no guarantee
that the final solution is in the feasible set. This is
particularly the case for the Unit Commitment
problem, which is a strongly constrained problem.
In this paper a new optimization strategy is
defined for the use of metaheuristics optimization
methods, leading to a satisfying solution and the
guarantee of its actual feasibility. The first step of
the procedure is to use an ant colony algorithm as a
“feasible solutions generator”. As such an algorithm
is constructive it is possible to explicitly manage the
163
Sandou G., Font S., Tebbani S., Hiret A. and Mondon C. (2008).
FEEDING A GENETIC ALGORITHM WITH AN ANT COLONY FOR CONSTRAINED OPTIMIZATION - An Application to the Unit Commitment Problem.
In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - ICSO, pages 163-168
DOI: 10.5220/0001488901630168
Copyright
c
SciTePress
constraints of the problem to create a set of feasible
solutions. The second step is to define a criterion to
optimize the problem with a genetic algorithm from
the initial population created by ant colony. In
section 2, the optimization strategy is depicted and
then is adapted to the Unit Commitment problem in
section 3. Numerical results are given in section 4.
Forthcoming works are given in section 5 and
concluding remarks are drawn in section 6.
2 OPTIMIZATION STRATEGY
2.1 Optimization Method Synopsis
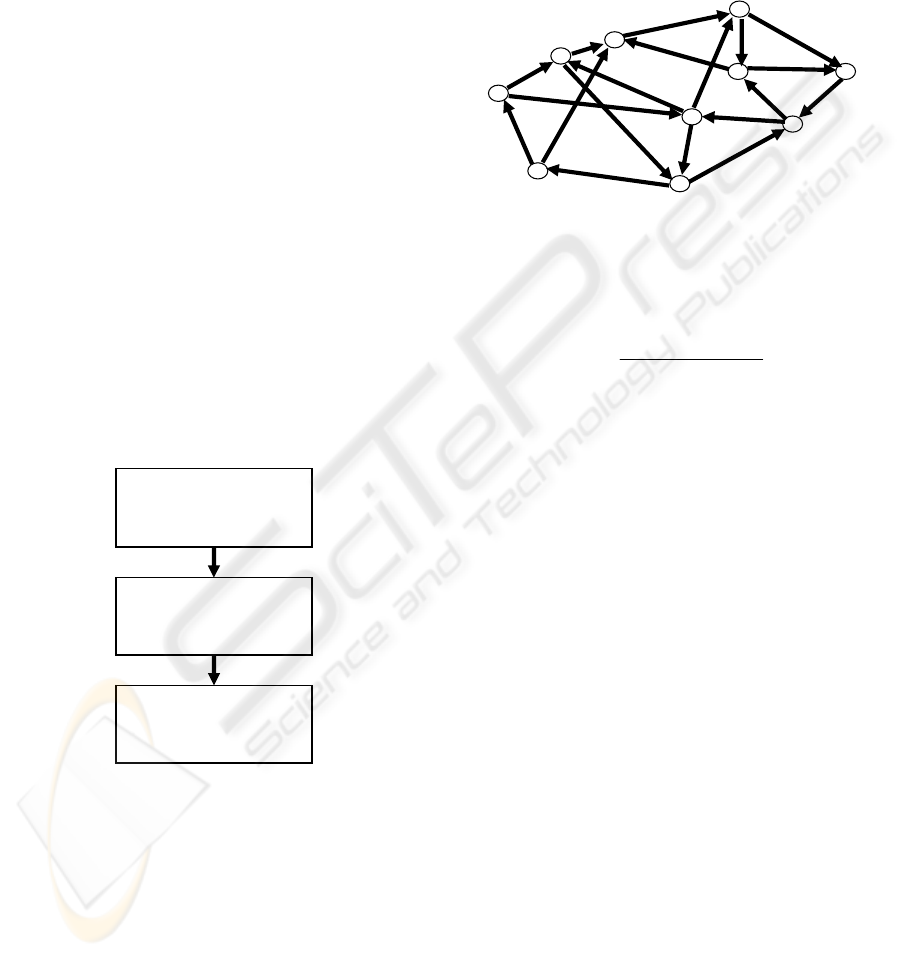
The synopsis of the algorithm is depicted on figure
1. The idea is to firstly sample the feasible space
with an ant colony algorithm. This algorithm is
constructive. Thus, solutions are explicitly built as
feasible ones (see section 2.2). However, ant colony
may fail to find a very good solution: because of its
positive feedback structure, it may be trapped in a
local minimum. Thus, a genetic algorithm will be
used to intensively explore the search space (see
section 2.4) from the population computed by ants.
For that purpose, a new criterion is defined, for
which feasibility is guaranteed (see section 2.3).
Compute initial
population with ant
colony algorithm
Compute a new
criterion, guaranteeing
feasibility
Intensively explore
search space with
genetic algorithm
Figure 1: Optimization strategy synopsis.
The proposed methodology can be used to solve
various and large scale optimization problems, the
satisfaction of all constraints being guaranteed.
2.2 Ant Colony Optimization
Ant colony optimization was introduced by Marco
Dorigo (Dorigo, et al., 1996). It is based on the way
ants are looking for food. The metaphor is used to
solve graph exploration problems. Various criterions
can be optimized. For instance, a cost may be
associated to each node. The goal is to minimize the
sum of costs while exploring the graph. This is the
well known Travelling Salesman Problem, for which
ant colony algorithm has been firstly used (Dorigo,
et al., 1997). During iteration t of the algorithm, F
ants walk on the graph of figure 2.
Edge ij
Node i
Node j
Figure 2: Graph exploration.
If ant f has reached node i , the probability that it
chooses the next node
j is:
.
)(
)(
)(
)(
)(
∑
∈
=
iJm
β
im
α
im
β
ij
α
ij
f
i
f
tτη
tτη
jp
(1)
)(tτ
ij
is the pheromone trail on edge ij during
iteration t. Its value depends on the results of
previous ants;
ij
η
is the attractiveness. It refers to the « local
choice ». For the Traveling Salesman Problem,
ijij
dη /1=
, where
ij
d
is the cost associated to
the edge
ij of the graph;
α
and β are weighting factors;
)(iJ
f
is the feasible set (for the travelling
Salesman problem, this feasible set contains all
nodes connected to node i, but those nodes
which have been already explored by the ant
are to be removed).
At the end of iteration t of the algorithm, F ants have
computed F potential solutions, which are evaluated.
The pheromone trail which laid on the graph of
figure 2 is then updated:
)(Δ)()1()1( tτtτρtτ
ijijij
+−=+
(2)
ij
τΔ
is the update coefficient whose value depends
on the results of ants in iteration t. The more the ants
which have walked on edge
ij have obtained good
results, the higher is
ij
τΔ . Several strategies can be
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
164
used for this update.
ρ
is the evaporation
coefficient. This coefficient is an analogy with
physical evaporation of pheromone in nature.
Usually, there are about 20 to 30 ants, and
2and1 ≈≈ βα . It is often necessary to bound the
pheromone trail on each edge (
],[
maxmin
σσσ ∈ ), to
avoid premature convergence; see (Stützle, et al.,
2000). Note that ant colony optimisation is a
constructive algorithm. As results, it can explicitly
take into account all the constraints of the problem,
with the help of the feasible sets
)(iJ
f
which are
built for each ant.
2.3 Defining a Feasibility Criterion
Consider the following optimization problem:
⎩
⎨
⎧
≤
=
0)(
0)(
.
)(min
xg
xh
ts
xf
x
(3)
If a feasible solution with cost
f
c is known, the
following feasibility criterion can be defined:
)()).()1(()(min xBxhcεxf
f
x
+++
(4)
where
ε is a small positive real;
)(xh is a penalty function.
)(xB is a boolean function with value 1 for
non feasible solutions and 0 for feasible ones.
Any unfeasible solution has a higher cost than the
feasible known solution. Then the criterion can be
optimized by any unconstrained optimization
algorithm, and for instance by genetic algorithm. In
the proposed strategy, c
f
is the cost of the best
solution found by the ant algorithm.
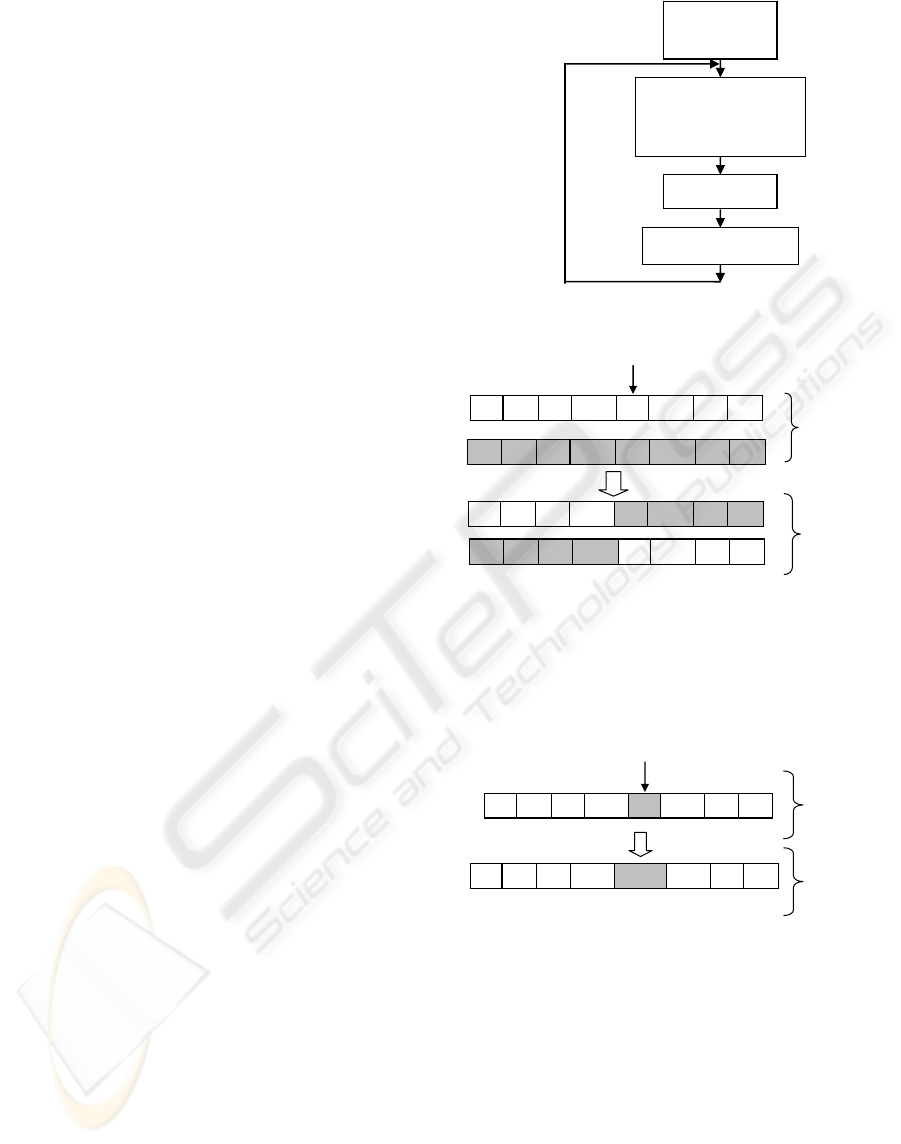
2.4 Genetic Algorithm
Genetic algorithm is a classical global optimization
method. The general flow chart of this algorithm is
given in figure 3. Classical cross-over and mutation
operators are represented in figure 4 and 5 for a
binary optimization problem. The aim of the
crossover operator is to create 2 new potentially
efficient individuals from 2 parents by mixing their
variables.
Initial
population
Genetic
operations : cross-
over, mutation
Selection
New population
Figure 3: General flow chart of a genetic algorithm.
1
x
2
x
K
1−i
x
i
x
1+i
x
K
n
x
1
y
2
y
K
1−i
y
i
y
1+i
y
K
n
y
1
y
2
y
K
1−i
y
i
x
1+i
x
K
n
x
1
x
2
x
K
1−i
x
i
y
1+i
y
K
n
y
Parents
Children
+
Crossing over point, randomly chosen
Figure 4: Crossing-over operator.
The mutation operator allows the introduction of
new genes in the population by randomly changing
one of the variables. The selection operator is made
via the classical biased roulette selection.
1
x
2
x
K
1−i
x
i
x
1+i
x
K
n
x
Parent
Mutation point, randomly chosen
Child
1
x
2
x
K
1−i
x
i
x
−
1
1+i
x
K
n
x
Figure 5: Mutation operator.
3 APPLICATION TO THE UNIT
COMMITMENT
3.1 Unit Commitment Problem
The Unit Commitment refers to the minimization of
global costs of K production units, over a time
horizon N, satisfying a consumer’s demand:
FEEDING A GENETIC ALGORITHM WITH AN ANT COLONY FOR CONSTRAINED OPTIMIZATION - An
Application to the Unit Commitment Problem
165
∑∑
==
−
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
N
n
K
k
k
n
k
n
k
s
k
n
k
n
k
prod
Qu
uuc
uQc
k
n
k
n
11
1
},{
),(
),(
min
,
(5)
where:
k
n
Q is the produced power of unit k at time n;
k
n
u is the on/off status of unit k at time n
(binary variable);
k
n
kk
n
kk
n
k
n
k
prod
uαQαuQc )(),(
01
+= is the cost
function of unit k (
k
i
α are technical data).
)1()1(),(
111
k
n
k
n
k
off
k
n
k
n
k
on
k
n
k
n
k
s
uucuucuuc −+−=
−−−
is the start up and shut down cost of unit k.
Constraints of the problem are:
Capacity constraints:
k
n
k
k
n
k
n
k
uQQuQ ≤≤
(6)
Satisfaction of consumer’s demand
dem
n
Q :
dem
n
K
k
k
n
QQ ≥
∑
=1
(7)
Time-up
k
up
T and time-down
k
d
T constraints:
⎟
⎠
⎞
⎜
⎝
⎛
===⇒
==
−+
++
−
1,,1,1
)1,0(
1
21
1
k
Tn
k
n
k
n
k
n
k
n
k
up
uuu
uu
L
(8a)
⎟
⎠
⎞
⎜
⎝
⎛
===⇒
==
−+
++
−
0,,0,0
)0,1(
1
21
1
k
Tn
k
n
k
n
k
n
k
n
k
d
uuu
uu
L
(8b)
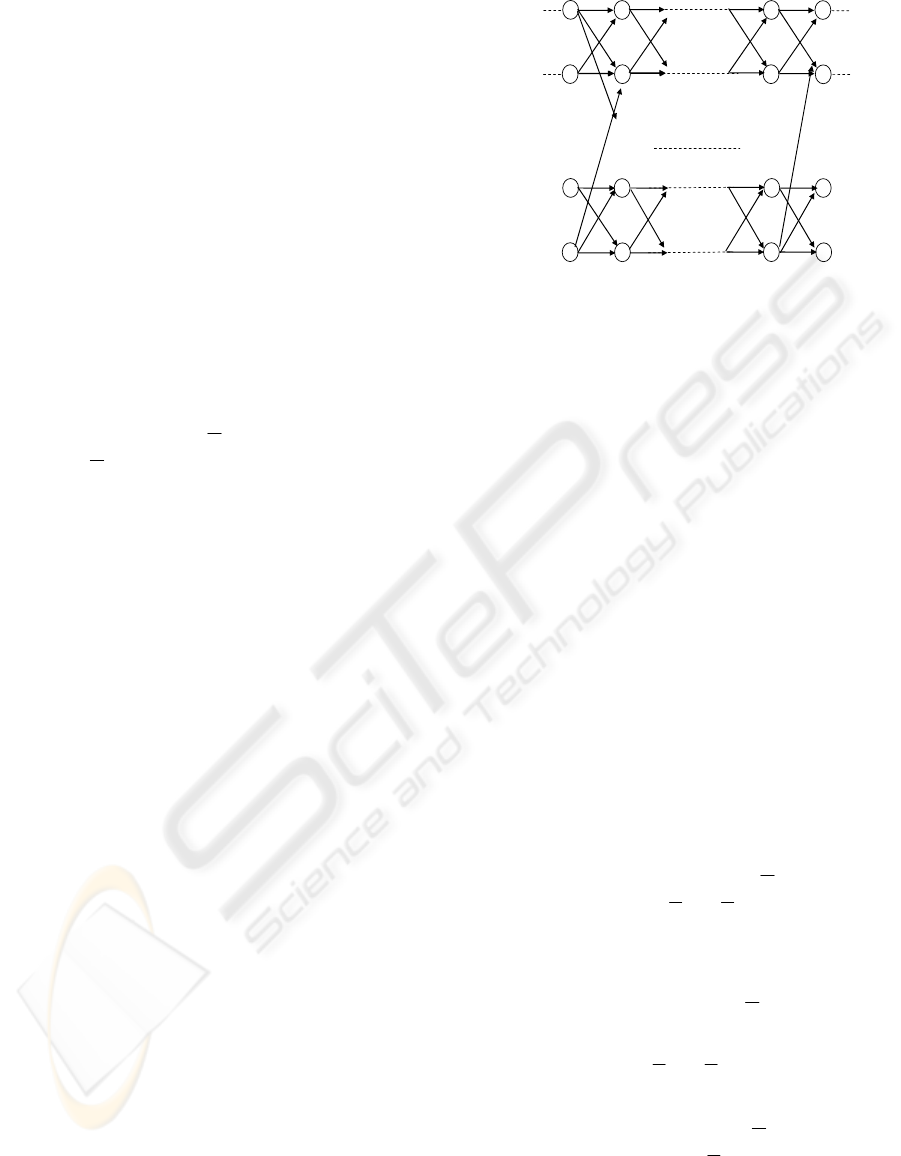
3.2 Graph Exploration Formulation
for Ant Colony
The Unit Commitment problem can be depicted by
the graph represented in figure 6. Nodes of the graph
are all the possible states of production system:
},,{
1 K
nn
uu K . The goal is to go from one of the
possible states at time 1, to one of the possible states
at time N, while satisfying all constraints and
minimising global costs. Start up/shut down are
associated to edges of the graph; production costs
are associated to nodes.
Time
interval 1
State 00…00
State 00…01
State 01…11
State 11…11
Time
interval 2
Time
interval N-1
Time
interval N
Figure 6: Graph exploration formulation of Unit
Commitment.
3.3 Computation of Real Variables
Ant colony and genetic algorithm are mostly
dedicated to integer programming. The problem can
be reformulated in a purely integer programming
problem. Consider that binary variables are given
and refer to a feasible solution. Real variables are
computed as the solution of the following
optimization problem:
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
∑∑
∑∑
==
==
−
N
n
K
k
k
n
k
n
k
Q
N
n
K
k
k
n
k
n
k
s
k
n
k
n
k
prod
Q
uQα
uuc
uQc
k
n
k
n
11
1
}{
11
1
}{
minarg
)),(
),((
minarg
(9)
The optimal solution is to produce as much as
possible with low-cost units, while satisfying
capacity constraints:
K
n
K
K
K
i
i
n
dem
n
K
n
k
n
k
k
K
ki
i
n
i
k
i
i
n
dem
n
k
n
n
K
i
i
n
i
dem
nn
uQQQQQ
uQ
QuQ
QQ
Q
uQQuQQQ
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎛
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎝
⎛
−
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
∑
∑
∑
∑
−
=
+=
−
=
=
,,maxmin
,
,
maxmin
,,maxmin
1
1
1
1
1
11
1
2
1
M
M
(10)
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
166
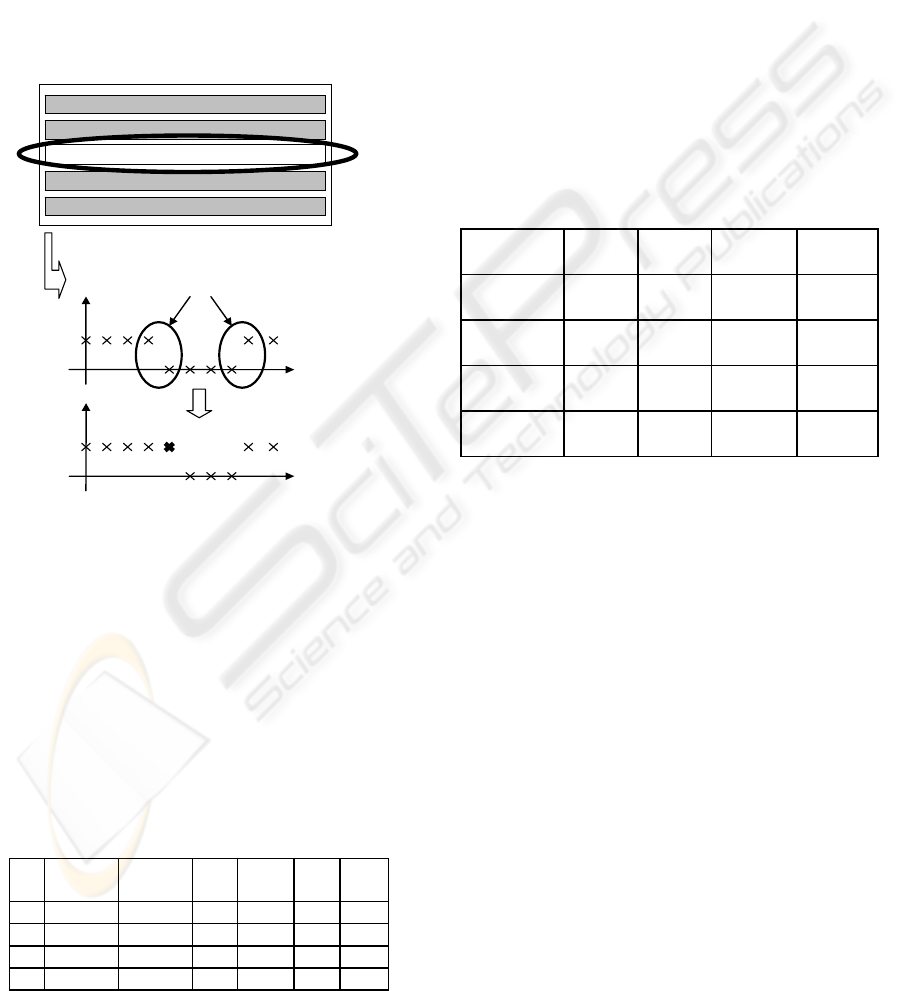
3.4 Enhanced Genetic Algorithm
It has been observed that the classical genetic
algorithm can be more efficient by using the a priori
knowledge of the system (Sandou, et al., 2007). A
“selective mutation operator” is added to the
classical genetic operators. Consider figure 7, with a
particular unit scheduling. Very often, a random
mutation leads to an infeasible solution, because of
time-up and time-down constraints. To increase the
probability of reaching a feasible point with a
mutation, the muted gene has to be located at
switching times of the planning.
1 1 1 1 1 1 0 0 0 0
Switching times :
Authorized
mutations
Figure 7: Selective mutation operator.
4 NUMERICAL RESULTS
The proposed strategy has been tested with Matlab
6.5 with a Pentium IV 2.5GHz. Optimization
horizon is 24 hours with a sampling time of one
hour. A comparison is made with pure genetic
algorithm. A “four unit” case is considered.
Characteristics are given in table 1.
on
c is 2€ and
off
c
is 10€ for all units.
Table 1: Characteristics of the “4 unit case”.
k
Q
min
(MW)
Q
max
(MW)
α
0
(€)
α
1
T
d
(h)
T
up
(h)
1
10 40 25 2.6 2 4
2
10 40 25 7.9 2 4
3
10 40 25 13.1 3 3
4
10 40 25 18.3 3 3
For this small case example, a “Branch and Bound”
method has been developed so as to gat the global
optimum and validate the method. Parameters of the
the ant colony algorithm are:
,2;1 == βα 2.0
=
ρ
,
5;1
maxmin
=
=
ττ . For the genetic algorithm,
parameters are: Crossover probability 70%, classical
mutation probability 5%, selective mutation: 10%.
Results are given in table 2. As stochastic algorithms
are considered, 100 tests are performed for each
case, and statistical data about the results are given:
mean cost (compared to the global optimum), worst
case, rate of success (number of times that the global
optimum is found) and computation times. The
population are set to 50 individuals for genetic
algorithm. When it is fed by ant colony, 5 iterations
of 10 ants are performed to compute 50 initial
solutions.
Table 2: Results for the “4 unit” case.
Mean Worst Success Comp.
times
Ants + GA
100 iter
+2.5% +9.4% 30% 15 s
GA
100 iter
+3.1% +13.4% 20% 13 s
Ants + GA
200 iter
+0.4% +3.5% 80% 25 s
GA
200 iter
+0.5% +4.5% 77% 24 s
Computation times are very low for all cases.
Results show that the use of ant colony as a “feasible
solutions generator” leads to an increase in the
quality of the solution. In particular, the worst case
cost is better with the cooperative method. Thus, the
cooperative method is very satisfying, especially for
the “50 Ants – GA 200 iterations” case, as the mean
result is just 0.4% higher than the optimal solution,
and the worst case leads to a slight increase (less
than 4%). Computation times are about 25 seconds.
For 200 generations, results seem to prove that
the ant generation has no influence anymore,
compared with the pure genetic algorithm. However,
for successful tests, it is interesting to have a look on
the iteration number for which the best solution has
been found. For pure generic algorithm, the best
solution is found after 126 generations (average
number), whereas it is found after 96 generations for
the ant colony/genetic algorithm. Convergence is
achieved earlier with the cooperative method. Note
that results of the pure genetic algorithm are still
very satisfying, thanks to the selective mutation
operator, as shown in (Sandou, et al., 2007).
FEEDING A GENETIC ALGORITHM WITH AN ANT COLONY FOR CONSTRAINED OPTIMIZATION - An
Application to the Unit Commitment Problem
167

5 DISCUSSION
5.1 Very Large Scale Cases
The interest of a feasible initial population has been
shown in previous results. In this paper, this feasible
population is computed by an ant algorithm. The ant
colony algorithm can be seen as a stochastic
dynamic programming algorithm. The size of the
state space is 2
K
. This is the main limiting point of
the proposed method. Thus, for high values of K, the
computation times of the ant colony algorithm grows
very quickly. Thus, one of the main points is the
application of ant colony to very large scale cases.
5.2 Global Optimization and
Cooperation
Ant colony algorithm and genetic algorithm are two
global optimization techniques and it may be
astonishing to use them as a cooperative method.
The goal of this hybridising was to couple the
feasibility properties of ant colony algorithm and the
intensive exploration of genetic algorithm. The
cooperation is a sequential procedure, and a more
alternated procedure could be profitable. For
instance, results of genetic algorithms can be used to
define the attractiveness parameters in a new
iteration of ant colony algorithms. Furthermore, it
will be interesting to couple the method with a local
search.
6 CONCLUSIONS
In this paper, an optimization strategy has been
defined and applied to solve the Unit Commitment.
The main idea is to use an ant algorithm as a feasible
solutions generator. These feasible solutions are
brought together in an initial population for a genetic
algorithm. To guarantee the feasibility of the final
solution, a special criterion is computed from the
results of the ant algorithm. To increase the
efficiency of the classical genetic algorithm, a
knowledge-based operator is defined (selective
mutation). Finally, the proposed method leads to
high quality solution, with guarantees of feasibility
and with low computation times. The main limiting
point appears to be the computation times of ant
colony algorithm for very large scale cases.
However, the use of feasible solutions in the initial
population of a genetic algorithm is an interesting
way to decrease the number of iterations required to
find near optimal solutions. Forthcoming works deal
with the use of such algorithm for predictive control
of non linear hybrid systems.
REFERENCES
Chen C.-L, Wang S.-C., 1993. Branch and Bound
scheduling for thermal generating units. In: IEEE
Transactions on Energy Conversion, 8(2), 184-189.
Dorigo M., Maniezzo V., Colorni A., 1996. The Ant
System: Optimization by a Colony of Cooperating
Agents. In: IEEE Transactions on Systems, Man and
Cybernetics-Part B, 26(1), 1-13.
Dorigo M., Gambardella, L. M., 1997. Ant Colony
System : a Cooperative Learning Approach to the
Traveling Salesman Problem. In: IEEE Transactions
on Evolutionary Computation, 1, 53-66.
Ouyang Z., Shahidehpour S. M., 1991. An intelligent
dynamic programming for unit commitment
application. In: IEEE Transactions on Power Systems,
6(3), 1203-1209.
Rajan C. C. A, Mohan M. R., 2004. An evolutionary
programming-based tabu search method for solving
the unit commitment problem. In: IEEE Transactions
on Power Systems, 19(1), 577-585.
Sandou, G., Font, S., Tebbani, S., Hiret, A., Mondon, C.,
2007. Enhanced genetic algorithm with guarantee of
feasibility for the Unit Commitment problem. In:
Proceeding of the 8
th
International Conference on
Artificial Evolution, Tours, France.
Sen S., Kothari D. P., 1998. Optimal Thermal Generating
Unit Commitment: a Review. In: Electrical Power &
Energy Systems, 20(7), 443-451.
Senjyu T., Shimabukuro, K., Uezato K. and Funabashi T.,
2004. A fast technique for Unit Commitment problem
by extended priority list. In: IEEE Transactions on
Power Systems, 19(4), 2119-2120.
Stützle T., Hoos, H. H., 2000. MAX-MIN Ant System, In:
Future Generation Computer Systems, 16, 889-914.
Swarup K., Yamashiro, S., 2002. Unit commitment
solution methodology using genetic algorithm. In:
IEEE Transactions on Power Systems, 17(1), 87-91.
Yin Wa Wong S., 1998. An Enhanced Simulated
Annealing Approach to Unit Commitment. In:
Electrical Power & Energy Systems, 20(5), 359-368.
Zhai Q; Guan X., 2002. Unit Commitment with identical
units: successive subproblems solving method based
on Lagrangian relaxation. In: IEEE Transactions on
Power Systems, 17(4), 1250-1257.
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
168
