SHAPE MEMORY ALLOY TENDONS ACTUATED TENTACLE
ROBOTIC STRUCTURE
Models and Control
*
Nicu George Bîzdoacă,
**
Anca Petrişor
*
Faculty of Automation,Computers and Electronics, University of Craiova, Romania
*
Elvira Bîzdoacă,
*
Ilie Diaconu,
**
Sonia Degeratu
**
Faculty of Electromechanical Engineering, University of Craiova, Romania
Keywords: Robotics, Shape memory alloy applications, Serial link, Fuzzy controller.
Abstract: A tentacle manipulator is a manipulator with a great flexibility, with a distributed mass and torque that can
take any arbitrary shape. Technologically, such systems can be obtained by using a cellular structure for
each element of the arm. Shape memory alloy actuation offers an interesting solution, using the shape
transformation of the wire/structure in the moment of applying a thermal type transformation able to offer
the martensitic temperature. In order to assure an efficient control of SMA actuator applied to inverted
pendulum, a mathematical model and numerical simulation of the resulting model is required. Due a
particular possibility SMA actuator connection, a modified dynamics for wire or tendon actuation is
presented. For an efficient study a Simulink block set is developed (block for user configurable shape
memory alloy material, configurable block for dynamics of single link robotic structure, block for user
configurable wire/tendon actuation). As conventional control possibilities were explored, the fuzzy control
structure applied in this paper, offer an improved response. A more compact SMA actuation is proposed and
experimented. The results are commented.
1 INTRODUCTION
Shape Memory Alloy (SMA) are materials that,
once mechanically deformed at given temperature,
are able to recover the deformation through an
appropriate thermal cycle (Funakubo, 1987).
Between the alloys that show this property,
attention has been focused on Nickel – Titanium
alloy: it show properties which are suitable for the
applications in robotics, general propose actuator
and medicine (Faravelli and Marioni, 1996). The
nickel titanium alloys, generally refereed to as
Nitinol are four times the cost of Cu-Zn-Al alloys,
but it possesses several advantages as greater
ductility, more recoverable motion, excellent
corrosion resistance, stable transformation
temperatures, high biocompatibility and the ability
to be electrically heated for shape recovery. Other
important proprieties of the Nitinol, superelasticity
(or pseudoelasticity) refers to the ability of NiTi to
return to its original shape upon unloading after a
substantial deformation.
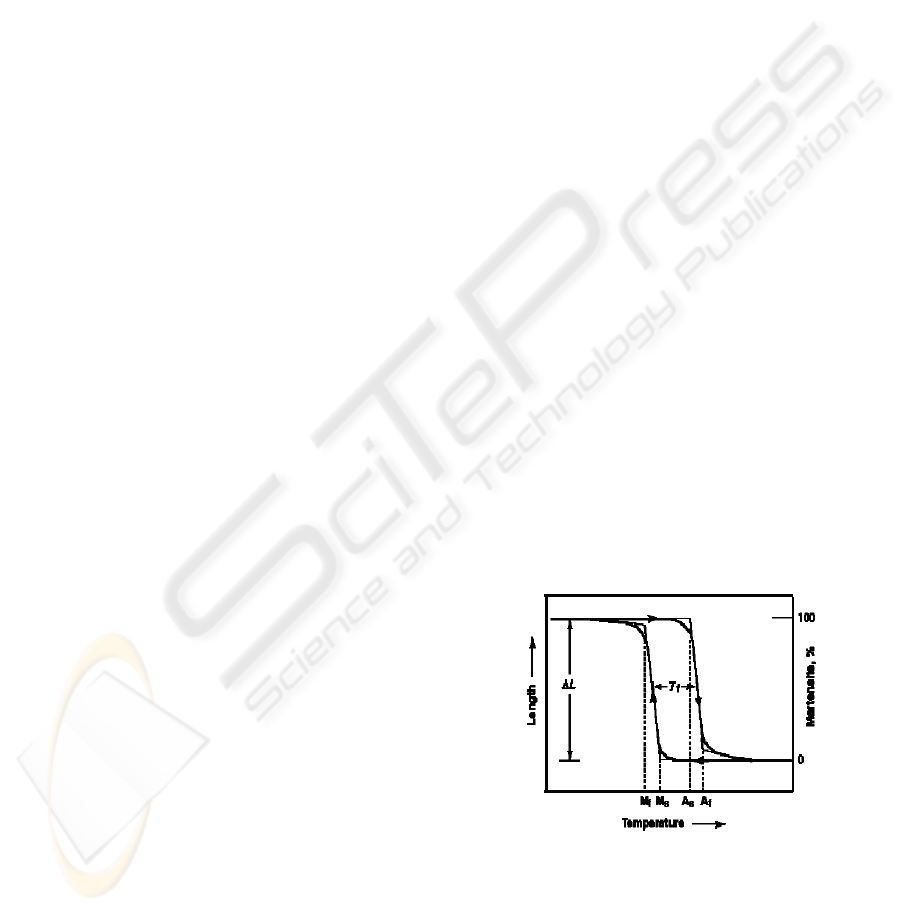
This is based on stress-induced martensite
formation. The application of an outer stress causes
martensite to form at temperatures higher than M
s
.
Figure 1: Martensitic and Austentic transformations.
The macroscopic deformation is accommodated
by the formation of martensite. When the stress is
released, the martensite transforms back into
austenite and the specimen returns back to its
original shape. Superelastic NiTi can be strained
several times more than ordinary metal alloys
77
George Bîzdoac
ˇ
a N., Petri¸sor A., Bîzdoac
ˇ
a E., Diaconu I. and Degeratu S. (2008).
SHAPE MEMORY ALLOY TENDONS ACTUATED TENTACLE ROBOTIC STRUCTURE - Models and Control.
In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - RA, pages 77-80
DOI: 10.5220/0001490800770080
Copyright
c
SciTePress

without being plastically deformed, which reflects
its rubber-like behavior. It is, however, only
observed over a specific temperature area. The
highest temperature at which martensite can no
longer stress induced is called Md. Above M
d
NiTi
alloy is deformed like ordinary materials by
slipping. Below as temperature, the material is
martensitic and does not recover. Thus,
superelasticity appears in a temperature range from
near A
f
and up to M
d
. The largest ability to recover
occurs close to A
f.
Another important feature of superelastic
materials is that their unloading curves are flat over
large strains. Thus, the force applied by a
superelastic device is determined by the temperature,
not by the strain as in conventional Hookian
materials. The basic rule for electrical actuation is
that the temperature of complete transformation to
martensite M
f
, of the actuator, must be well above
the maximum ambient temperature expected.
2 DYNAMICS OF TWO-LINK
TENDON-DRIVEN ROBOTIC
STRUCTURE
There are many methods for generating the dynamic
equations of mechanical system. All methods
generate equivalent sets of equations, but different
forms of the equations may be better suited for
computation different forms of the equations may be
better suited for computation or analysis..
Using the kinetic energy and Lagrange methods
results:
()
111
cc ss
22 22221
222
1
11
2
cs0
221
22
⎡⎤⎡ ⎤
α+β δ+ β − β θ − β θ +θ
⎡⎤
⎢⎥⎢ ⎥
θ
+•
⎢⎥
⎢⎥⎢ ⎥
θ
⎢⎥
⎢⎥⎢ ⎥
⎣⎦
δ+ β δ β θ
⎢⎥⎢ ⎥
⎣⎦⎣ ⎦
&&&
&&
&&
&
⎥
⎦
⎤
⎢
⎣
⎡
⎥
⎦
⎤
⎢
⎣
⎡
=•
2
1
2
1
τ
τ
θ
θ
&
&
(1)
Where
(
)
(
)
(
)
mm
22 22 2 22
12
lw lw mrmlr
12
11 22 1 12
12 12
α= ++ ++ + +
(2)
mll
212
β=
(3)
(
)
m
22 2
2
lw mr
22 22
12
δ= + +
(4)
with w
1
, w
2
, l
1
, l
2
the width and respectively the
length of link 1 and link 2.
Figure 2: Two link robotic architecture.
3 SHAPE MEMORY ACTUATOR
STRUCTURE
Due the actuation architecture a simple
mathematical model can be establish. Schematically
the shape memory actuation is
Figure 3: Shape memory alloy actuation structure.
In Figure 3 l
v
is the variable length of shape
memory alloy wire, the l is the robotic link length
between the articulation point and the shape memory
alloy wire connection, r is the distance between the
second end of the SMA wire (which is a fixed point)
and the articulation point of the link (fixed point
too).
Using simple mathematical computation the
mathematical dependence can be established
(
)
222
v
1
lrl
arccos
2lr
⎛⎞
−+
⎜⎟
θ=
⎜⎟
⎜⎟
⎝⎠
()
2
1v
fl⇔θ =
(5)
The graphic of θ
1
as function of lv (considering
the real domain variation for
[
]
1
0,θ∈ π
) is linear,
that the liniarisation in modeling can be done
successfully.
The explanations concern the structural variation
of SMA actuator, which are limited superior by l
v
and inferior by 0.5 l
v
. The mathematical model
including the SMA actuation can be developed in
two ways: First is possible to consider for position
control, ONLY the length variation of the SMA
actuator. This approach is a correct one, the
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
78
additional torque, provided by the particular
proprieties of SMA, enforces the actuation. The
situation corresponds to tendon actuation or wire
actuation. Using the substitution:
v
1v
2
22 2
v
2l
l
llr
lr 4
lr
−
θ=
⎛⎞
−−
−
⎜⎟
⎜⎟
⎝⎠
&
&
(6)
2
v
1vv
22
22 2 22 2
vv
2l
2
ll
llr llr
lr 4 lr 4
lr lr
−
θ= − −
⎛⎞ ⎛⎞
−− −−
−−
⎜⎟ ⎜⎟
⎜⎟ ⎜⎟
⎝⎠ ⎝⎠
&& &
&&
(
)
22 2 2
vv
2
v
2
2
22 2
33
v
3
4l l l r
l
llr
lr 4
lr
−−
−
⎛⎞
⎛⎞
−−
⎜⎟
−
⎜⎟
⎜⎟
⎜⎟
⎝⎠
⎝⎠
&
(7)
Analyzing the equilibrium conditions, results
that
()
111
bτ= θ and
222
v
lrl=+, state which
correspond to real case.
Second way makes a simplifying assumption:
because the SMA connection with single link
structure can be choose near to the articulation point,
we can assume that the entire SMA torque is directly
used for movement. Then the mathematical model
can be expressed as
()
()
2
11 1
11
SMA 1 1 1
gm w cos
mw
b
32
⎛⎞
θ
τ= θ+ +θ
⎜⎟
⎜⎟
⎝⎠
&&
(8)
4 CONTROL OF SHAPE
MEMORY ALLOY TENTACLE
ROBOTIC STRUCTURE
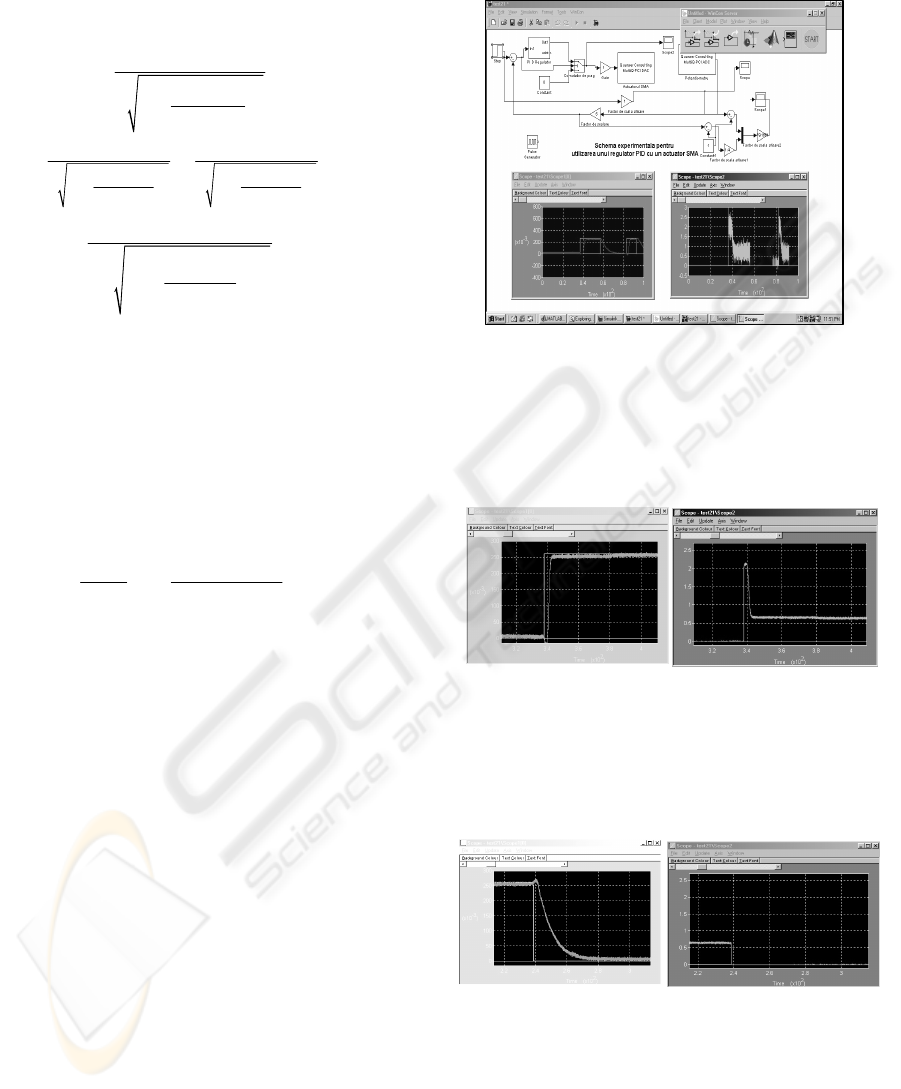
In order to investigate the SMA robotic structure
comportment a Quanser modified platform was used
for experiments. The basic control structure uses a
configurable PID controller and a Quanser Power
Module Unit for energizing the SMA actuators.
In order to investigate the SMA robotic structure
comportment a Quanser modified platform was used
for experiments. The basic control structure uses a
configurable PID controller and a Quanser Power
Module Unit for energizing the SMA actuators.
PID controller was changed, in order to adapt to
the particularities of the SMA actuator. A negative
command for SMA actuator corresponds to a
cooling source. The actual structure use for cooling
only the ambient temperature.
The best results arise when a PI controller is
used. The PI experimented controller parameters are:
the proportional parameter K
R
=10 and the
integration parameter is K
I
=0, 05.
Figure 4: Quanser modified platform.
The input step is equivalently with 30
0
angle
base variation and the evolution of this reference is
represented with the response of real system in
Figure 5. The control signal variation is presented in
Figure 6.
Figure 5: System response,
for step input.
Figure 6: PI controller
response, for step input.
For negative step, the evolution of the system
and the control variable evolution are presented in
Figure 7 and Figure 8.
Figure 7: System response,
negative step input.
Figure 8: PI controller
response, negative step
input.
Using PID, PD controller the experiments
conduct to less convenient results from the point of
view of time response or controller dynamics.
SHAPE MEMORY ALLOY TENDONS ACTUATED TENTACLE ROBOTIC STRUCTURE - Models and Control
79
Using heat in order to activate SMA wire, a
human operator will increase or decrease the amount
of heat in order to assure a desired position to
robotic link. Because of medium temperature
influence, can not be establish, apriori, a clear
control law, available for all the points of the robotic
structure workspace. A simple and efficent control
structure can be implemented.
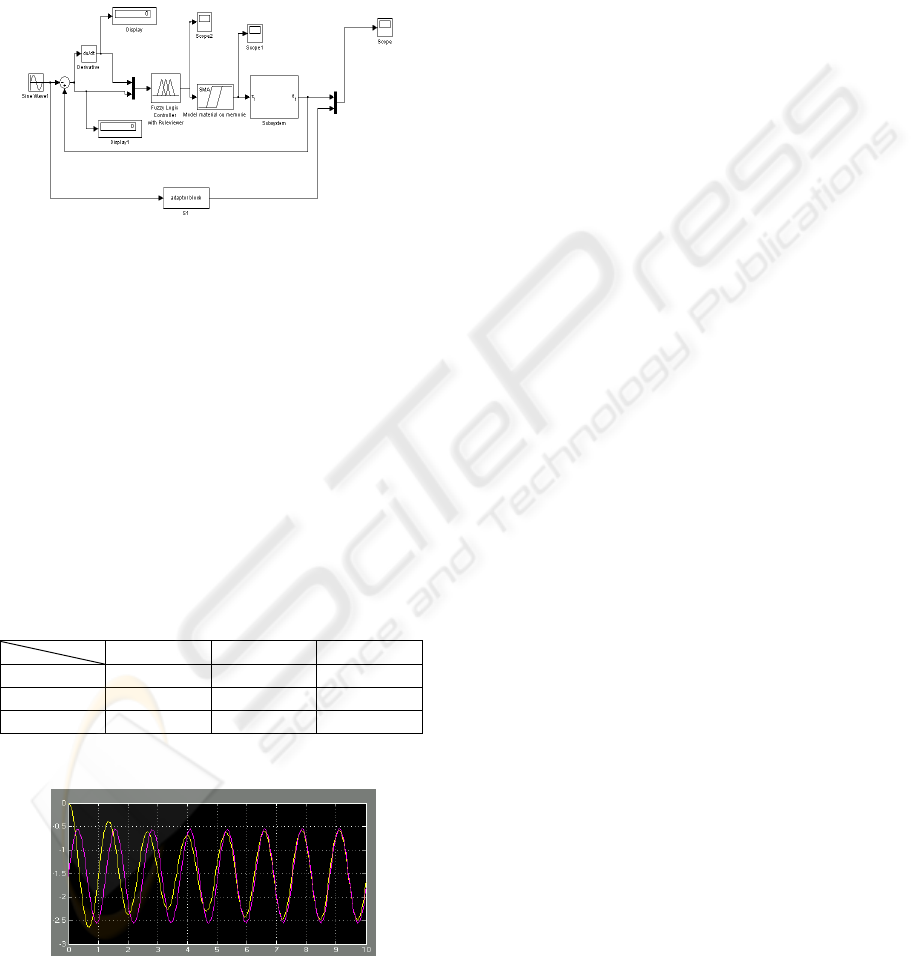
Figure 9: Fuzzy control structure.
For an efficient control it is proposed the
following definition for input and output members:
- input 1 is the first derivate of pozition error, with 3
fuzzy member: Negative, Zero, Pozitive
- input 2 is pozition error with 3 fuzzy member:
Negative, Zero and Pozitive
- output is temperature heating with 3 fuzzy
member: Temperature Negative (temperature under
austenitic start transformation), Temperature Zero
(temperatures between start and final austenitic
transformation), Temperature Positive (temperature
above temperature of final austenitic
transformation).
Table 1: Fuzzy rules for the proposed controller.
e
&
e
P Z N
P TP TP TP
Z TZ TZ TZ
N TN TN TN
The result of the numerical simulation are
promising, related to the simplicity of the control
structure, for the case of the sinusoidal reference
with frecvency of 5 rad/sec.
Figure 10: Fuzzy robotic structure output evolution.
5 CONCLUSIONS
The simulations, the mathematical model and the
initial experiments developed in the article offer a
background in studying the serial link robotic
control possibilities. The results respect the real
evolution of the structure. In the future, the authors
will explore improvement of the control
performnces and the extension of the experiments to
n link robotic structure.
REFERENCES
Cheng, F. T., "Control and Simulation for a Closed
Chain Dual Redundant Manipulator System",
Journal of Robotic Systems, pp. 119 - 133, 1995
Cheng, F. T., Orin,D. E., "Optimal Force Distribution
in Multiple-Chain Robotic Systems", IEEE Trans. on
Sys. Man and Cyb.", Jan., 1991, vol. 21, pp. 13 – 24
Cheng, F. T., Orin,D. E., , "Efficient Formulation of
the Force Distribution Equations for Simple Closed -
Chain Robotic Mechanisms", IEEE Trans on Sys.
Man and Cyb.,Jan. 1991, vol. 21, pp. 25 -32.
Delay, L., Chandrasekaran M., 1987. Les Editions
Physique. Les Ulis.
Faravelli L and Marioni A, 1996, Exploiting SMA Bars in
Energy Dissipators, Proceedings of the 2nd
International Workshop on Structural Control, Hong
Kong HKUST 41-50
Funakubo H., 1987, Shape Memory Alloys, Gordon and
Breach Science Publishers
Ivanescu, M., Dynamic Control for a Tentacle
Manipulator, Proc. of Int. Conf., Charlotte, USA,
1984
Ivanescu, M.,Stoian,V., A Variable Structure Controller
for a Tentacle Manipulator, Proc. of the 1995 IEEE
Int.Conf. on Robotics and Aut., Nagoya, Japan, May
21 - 27,1995, vol. 3, pp. 3155 - 3160
Lotfi A. Zadeh , Fuzzy sets, Information and Control 8,
338-353, 1965.
Mason, M. T., "Compliance and Force Control",
IEEE Trans. Sys. Man Cyb., Nr. 6, 1981, pp. 418 –
432
Ross, T.J., Fuzzy Logic with Engineering Applications,
Mc.Grow Hill , Inc., 1995
Soo Yeong Yi, A robust Fuzzy Logic Controller for Robot
Manipulators, IEEE Trans. on Systems, Man and
Cybernetics, vol 27, No 4, 706-713, 1997
Tao, C.W. ,Design of Fuzzy-Learning Fuzzy Controllers ,
FUZZ IEEE'98, 416-421
Utkin, V. I., Variable structure systems with sliding
modes, IEEE Trans. Automat. Contr., vol. AC-22, pp.
212-222, 1977.
Utkin, V. I., Variable structure systems and sliding
mode\—State of the art assessment, Variable Structure
Control for Robotics and Aerospace Applications, K.
D. Young, Ed. , New York: Elsevier, pp. 9-32, 1993.
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
80
