THE PARALLELIZATION OF MONTE-CARLO PLANNING

Parallelization of MC-Planning

S. Gelly, J. B. Hoock, A. Rimmel, O. Teytaud

TAO (Inria), Lri, UMR Cnrs 8623, Univ. Paris-Sud, France

Y. Kalemkarian

High Performance Calculus, Bull, Grenoble, France

Keywords:

Bandit-based Monte-Carlo planning, parallelization, multi-core machines, message-passing.

Abstract:

Since their impressive successes in various areas of large-scale parallelization, recent techniques like UCT and

other Monte-Carlo planning variants (Kocsis and Szepesvari, 2006a) have been extensively studied (Coquelin

and Munos, 2007; Wang and Gelly, 2007). We here propose and compare various forms of parallelization of

bandit-based tree-search, in particular for our computer-go algorithm XYZ.

1 INTRODUCTION

Dynamic programming (Bellman, 1957; Bertsekas,

1995) provides a robust and stable tool for dynamic

optimization. However, its application to large scale

problems is far from simple and involves approxima-

tions, as in approximate value functions in approxi-

mate dynamic programming (Powell, 2007). Some

alternate approaches, like using simulations for focus-

ing on more important areas of the state space as in

RTDP (Barto et al., 1993), have provided some im-

portant yet unstable tools for large scale approximate

dynamic programming. Monte-Carlo planning, ap-

plied to Go since (Bruegmann, 1993), and in partic-

ular Bandit-based Monte-Carlo planning (Kocsis and

Szepesvari, 2006a), provides an alternate solution, in-

creasing the importance of simulations. Bandit-based

Monte-Carlo planning features the construction of a

tree approximating incrementally the distribution of

possible futures. Tools from the bandit literature (see

(Lai and Robbins, 1985; Auer et al., 2001); adversar-

ial case in (Kocsis and Szepesvari, 2005); huge sets

of arms in (Banks and Sundaram, 1992; Agrawal,

1995; Dani and Hayes, 2006; Berry et al., 1997))

are used in order to bias the random development

of the tree in the direction of the most important

directions; the important paper (Kocsis and Szepes-

vari, 2006a) applies recursively bandits for the bi-

ased random development of a tree. The efﬁciency

of recursive bandits is also shown by some chal-

lenges won by such methods (Hussain et al., 2006).

Its application to computer-go has provided partic-

ularly impressive results (Coulom, 2006; Wang and

Gelly, 2007). The decision taking, at each step, is far

more expensive, but the overall cost is much lower

than the computational cost of one dynamic program-

ming loop when the branching factor (or the state

space) is large. The analysis of Monte-Carlo plan-

ning if far from being closed, as it is not clear that

upper-conﬁdence bounds are the best tool for that,

in particular when heuristics like AMAF(Bruegmann,

1993) (also termed RAVE) are included. However, we

here consider a ﬁxed empirically tuned algorithm, and

we focus on its parallelization, for various forms of

parallelization (multi-core machines, standard clus-

ters). The application to computer-go is one of the

most illustrative applications of bandit-based Monte-

Carlo planning methods. In particular, Go is still far

from being solved, as moderate human players are

still much better than the best computer-go programs.

Monte-Carlo planning is a revolution in computer-

go, in some cases combined with tactical knowledge

(Cazenave and Helmstetter, 2005; Coulom, 2007) but

also in some cases almost from scratch without any

speciﬁc knowledge (Wang and Gelly, 2007), except

some likelihood of random playouts. The paralleliza-

tion of Monte-Carlo planning is classical in the multi-

core case; we here provide an analysis of the speed-

up of this multi-core approach (shared memory). We

then move to the message-passing architecture, for

244

Gelly S., B. Hoock J., Rimmel A., Teytaud O. and Kalemkarian Y. (2008).

THE PARALLELIZATION OF MONTE-CARLO PLANNING - Parallelization of MC-Planning.

In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - ICSO, pages 244-249

DOI: 10.5220/0001502402440249

 SciTePress

a cluster-parallelization. We brieﬂy introduce ban-

dits and bandit-based Monte-Carlo planning below,

for the sake of clarity of notations. We then present

the multi-core parallelization in section 2, and two

different approaches for the cluster parallelization in

section 3, 3.1. A bandit problem is typically deﬁned

as follows: (1) A ﬁnite set A = {1, ...,N} of arms

is given. (2) Each arm a ∈ A is equipped with an un-

known probability of reward p

. (3) At each time step

t ∈ {1, 2,...}, the algorithm chooses a

∈ A depend-

ing on (a

,. .. ,a

t−1

) and (r

,. .. ,r

t−1

). (4) The ban-

dit gives a reward r

, with r

= 1 with probability p

(independently), and r

= 0 otherwise. A bandit al-

gorithm is an algorithm designed for minimizing the

so-called regret:

Regret = T inf

a∈A

−

∑

i=1

Important results, depending on assumptions on the

set of actions and their distributionof rewards, include

(Lai and Robbins, 1985; Auer et al., 2001; Banks and

Sundaram, 1992; Agrawal, 1995; Dani and Hayes,

2006; Berry et al., 1997; Hussain et al., 2006; Kocsis

and Szepesvari, 2005; Coquelin and Munos, 2007). A

bandit is said to have side information if some infor-

mation other than the reward is available to the algo-

rithm. We present various bandit algorithms in sec-

tion 1: these bandit algorithms usually work as fol-

lows for each time step:

- compute a score, for each possible arm, which

consists in (i) an exploitation term, larger for arms

for which the average rewards in the past is good;

(ii) an exploration term, larger for arms which

have not been tried often.

- choose the arm with maximum score.

Typical improvements are: (i) give heuristically a

score to arms which have not been visited yet (see e.g.

(Wang and Gelly, 2007; Coulom, 2007)); (ii) guess

some side information (see the AMAF heuristic e.g.

(Gelly and Silver, 2007)); (iii) restrict the sampling to

the k(t) ﬁrst nodes for k(t) some non-decreasingmap-

ping (see progressive widening in (Coulom, 2007)).

In the case of Go and more generally bandit-based

Monte-Carlo planning, we use one bandit at each

node of the tree, as explained in section 1. The dif-

ﬁcult elements are the anytime nature of the problem,

its non stationarity (Hussain et al., 2006; Kocsis and

Szepesvari, 2006b), its large number of arms (Banks

and Sundaram, 1992). The side information (usually

termed AMAF) is detailed below.

This section provides an overview of bandit-based

Monte-Carlo planning algorithms. It is presented in

the case of a game; the experiments are performed in

the case of Go. We point out that UCT can be applied

to trees far from minimax problems: max/max prob-

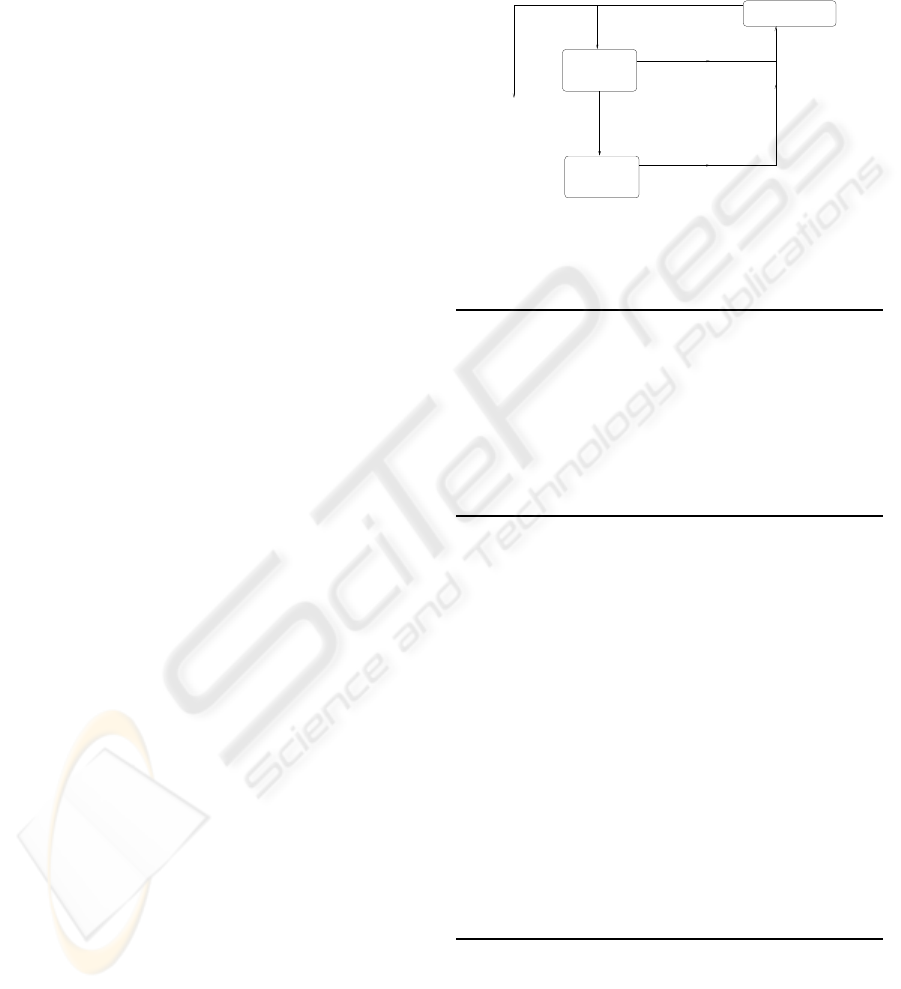
lems, or max/Expectation, etc. Algorithm 1 provides

an overview (see also ﬂowchart in Fig. 1), and Algo-

rithm 3 provides a more detailed presentation. The

Choose a path

in the tree

(using statistics)

Node L’ out

of the tree

Simulation

over

Simulation S’

out of the tree

Complete

Game

Update the

and reward

and its reward

tree and its statistics

Time left > 0 ?

Yes

Decision

(most simulated

move from the root)

from L’ to game

Simulation

S in the tree

of the tree

and node L’ out

S,L,L’,S’

Figure 1: Flow chart of UCT. The bandit algorithm is ap-

plied in the simulation part in the tree.

Algorithm1: Monte-Carlo planning algorithm. The ﬁnal

line chooses the decision with the conservative rule that the

most simulated decision should be chosen. Other solutions,

such as taking the decision with the higher ratio ”number

of winning simulations divided by the number of simula-

tions”, are too much dangerous because a decision might

be very poor due to a small number of simulations. Some

other robust and elegant techniques include the use of lower

conﬁdence bounds. Here, rewards are binary (win or loss),

but arbitrary distributions of rewards can be used.

Initialize T to the root, representing the current state. T is

a tree of positions, with each node equipped with statis-

tics.

while Time left > 0 do

Simulate one game until a leaf (a position) L of T

(thanks to bandit algorithms). Then, choose one son

(a successor) L

′

of L.

Simulate one game from position L

′

until the game is

over.

Add L

′

as a son of L in T.

Update statistics in all the tree. In UCT, each node

knows how many winning simulations (from this

node) have been performed and how many simula-

tions (from this node) have been performed. In other

forms of tree-search, other informations are neces-

sary (heuristic information in AMAF, total number

of nodes in the tree in BAST(Coquelin and Munos,

2007)).

end while

Pick up the decision which has been simulated most often

from the root.

main point in Algorithm 1 is that the tree is unbal-

anced, with a strong bias in favor of important parts

of the tree. The function used for taking decisions out

of the tree (i.e. the so-called Monte-Carlo part) is de-

ﬁned in (Wang and Gelly, 2007) The function used

for simulating in the tree is presented in Algorithm

THE PARALLELIZATION OF MONTE-CARLO PLANNING - Parallelization of MC-Planning

245

2. This function is a main part of the code: it de-

cides in which direction the tree should be extended.

There are variousformulas, all of them being based on

the idea of a compromise between exploitation (fur-

ther simulating the seemingly good moves) and ex-

ploration (further simulating the moves which have

not been explored a lot). The empirically best tool in

Algorithm 2: Taking a decision in the tree. The total

number of simulations at situation s is Simulations(s) =

∑

Simulations(s,d). We present here various formulas for

computing the score (see (Lai and Robbins, 1985; Auer

et al., 2001; Gelly and Silver, 2007) for UCB1, UCB-

Tuned and AMAF respectively); other very important vari-

ants (for inﬁnite domains, larger number of arms, of spe-

ciﬁc assumptions) can be found in (Banks and Sundaram,

1992; Agrawal, 1995; Dani and Hayes, 2006; Coquelin and

Munos, 2007).

Function decision = Bandit(situation s in the tree).

for d in the set of possible decisions do

Let ˆp(d) = Wins(s,d)/Simulations(s,d).

SWITCH (bandit formula):

- UCB1: compute score(d) = ˆp(d) +

2log(Simulations(s))/Simulations(s,d).

- UCB-Tuned.1: compute score(d) = ˆp(d) +

V log(Simulations(s))/Simulations(s,d) with

V = max(0.001, ˆp(d)(1− ˆp(d))).

- UCB-Tuned.2: compute score(d) = ˆp(d) +

V log(Simulations(s))/Simulations(s,d) +

log(Simulations(s))/Simulations(s,d) with

V = max(0.001, ˆp(d)(1− ˆp(d))).

- AMAF-guided exploration: Compute

score(d) = α(d) ˆp(d) + (1−α(d))

ˆp(d) with:

ˆp(d) the AMAF-estimate of the asymptotic

value of score(d).

- α(d) a coefﬁcient depending on

Simulations(s,d) and the AMAF-conﬁdence

ˆp(d) (see (Gelly and Silver, 2007)).

END SWITCH

end for

Return argmax

score(d).

Algorithm 2 is the AMAF-guided exploration. In that

case, in the classical formalism of bandits, each time

one arm is played, we get: (i) a positive or null reward

for the chosen arm (0 or 1); (ii) a list of arms, consist-

ing in half of the arms roughly, positively correlated

with the list of arms for which the rewards would

have been positive if these arms have been played.

The bandit algorithm for this bandit problem has been

empirically derived in (Gelly and Silver, 2007). To

the best of our knowledge, there’s no mathematically

grounded bandit algorithm in that case. An important

improvement (termed progressive widening(Coulom,

2007)) of Algorithm 2 consists in considering only

the K(n) ”best” moves (the best according to some

heuristic), at the n

simulation in a given node, with

K(n) is an non-decreasing mapping from N to N.

Algorithm 3: More detailed Monte-Carlo planning algo-

rithm.

Initialize T to the root, representing the current state. T

is a tree of positions.

while Time left > 0 do

Simulate one game until a leaf (a position) L of T

(thanks to bandit algorithms applied until a leaf is met,

see Algorithm 2).

Choose one son (a successor) L

′

of L, possibly with

some ofﬂine learning (Gelly and Silver, 2007).

Simulate one game from position L

′

until the game is

over.

Add L

′

as a son of L in T.

Update statistics in all the tree. In UCT, each node

knows how many winning simulations (from this

node) have been performed and how many simula-

tions (from this node) have been performed. In other

forms of tree-search, other informations are neces-

sary (heuristic information in AMAF, total number

of nodes in the tree in BAST(Coquelin and Munos,

2007)).

end while

Pick up the decision which has been simulated most often

from the root.

2 MULTI-CORE

PARALLELIZATION

The multi-core parallelization is intuitively the most

natural one: the memory is shared. We just have

to distribute the loop on various threads (each thread

performs simulations independently of other threads,

with just mutexes protecting the updates in memory),

leading to algorithm 4. Consider N the number of

Algorithm 4: Multi-core Monte-Carlo planning algorithm.

Initialize T to the root, representing the current state. T

is a tree of positions.

For each thread simultaneously:

while Time left > 0 do

Simulate one game until a node (=position) L of T

(thanks to bandit algorithms); put this simulation S in

memory. Choose a successor L

′

of L.

Simulate one game from position L

′

until the game is

over; put this simulation S

′

in memory.

Add L

′

as a son of L in T.

Update statistics in all the tree thanks to S and S

′

end while

Pick up the decision which has been simulated most of-

ten.

threads. The number of simulations per second is

typically almost multiplied by N. However, this algo-

rithm is not equivalent to the sequential one: possibly,

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

246

Table 1: Success rate against mogoRelease3, for various

computation times. Under the two-assumptions (1) almost

N times more simulations per second with N cores (2) no

impact of the ”delay” point pointed out in the text, the

speed-up would be linear and all the raws would be equal.

We see a decay of performance for 4 threads.

Nb threads × 10 20 40

comp. time sec.procs secs.procs secs.procs

1 thread 51.1 ± 1.8 62.0 ± 2.2 74.4 ± 2.4

2 threads 62.9 ± 1.8

4 threads 66.4 ± 2.1

N−1 simulations are running when one more simula-

tion is launched, and the updates of T corresponding

to these N − 1 simulations are not taken into account.

There is a N − 1 delay, and the analysis of the delay is

not straightforward - we will quantify this effect ex-

perimentally. We get the following empirical results:

Table 1 conﬁrms the roughly 63% success rate known

when doubling the computational power. As a con-

clusion, in 9x9 Go, the speed-up of the multi-core al-

gorithm 4 is linear for two nodes, slightly below the

linear speed-up for 4 nodes (by interpolation, we can

estimate the speed-up as 3 for 4-cores).

3 CLUSTER PARALLELIZATION

First, let’s consider the generalization of the multi-

core approach to a cluster, i.e. a version with mas-

sive communication in order to keep roughly the same

state of the memory on all nodes. As the mem-

ory is not shared here, we have to broadcast on the

network many update-informations; each simulation

on one node leads to one broadcast. Possibly, we

can group communications in order to reduce laten-

cies. This leads to the algorithm 5. T = 0 is per-

haps possible, for high performance clusters or pro-

cessors inside the same machine. Let’s consider the

idealized case of a cluster with negligible communi-

cation cost and inﬁnite number of nodes. Let’s as-

sume that a proportion α of time is spent in the up-

dates. Also, let’s assume that the delay of updates

does not reduce the overall efﬁciency of the algo-

rithm. What is the speed-up in that case ? Consider

M the number of simulations per second on one node

in the (mono-node) case. With N nodes, at each time

steps, we get NM simulations. The number of up-

dates is therefore NM per second of simulation. If

the time of one update is T, for each group of M

simulations, (i) each node performs M simulations

(costs 1− α second); (ii) each node sends M update-

information (costs 0 second); (iii) each node receives

Algorithm 5: Cluster algorithm for Monte-Carlo planning.

As there are many paths leading to the same node, we must

use a hash table, so that with some key (describing a goban)

we can ﬁnd if a node is in the tree and what are its statistics

in constant time.

for Each node do

Initialize T to the root, representing the current state

of the root. T is a tree of positions, with statistics at-

tached to each node.

end for

for For each computer simultaneously: do

for For each thread simultaneously: do

while Time left > 0 do

Simulate one game until a node (=position) L of

T (thanks to bandit algorithms); put this simula-

tion S in memory. Choose a successor L

′

of L.

Simulate one game from position L

′

until the

game is over; put this simulation S

′

in memory.

S,S

′

is a complete game starting at the root.

Add L

′

as a son of L in T, and update all the

statistics in T with S, S

′

Add (L, L

′

,S, S

′

) to a stack of to-be-sent simula-

tions.

if time−t0 ≥ T and thread=ﬁrst thread then

Set t0 = time.

Send all the (L,L

′

,S, S

′

) in the stack to all

other nodes.

Reset the stack.

Receive many (L,L

′

,S, S

′

) from all other

nodes.

for Each (L,L

′

,S, S

′

) received do

Add L

′

as a son of L in T (if not present).

Update all the statistics in T with S, S

′

end for

end if

end while

end for

Pick up the decision which has been simulated most of-

ten.

(N − 1)M update-informations (costs 0 second); (iv)

each node updates its tree with these (N − 1)M up-

date informations (costs α(N − 1) second). If we di-

vide by the number N of nodes and let N → ∞, we

get (i) a cost (1− α)/N → 0; (ii) a cost 0 for send-

ing update-informations; (iii) a cost 0 for receiving

update-informations; (iv) a cost α(N − 1)/N → α for

updates. This implies that the main cost is the update-

cost, and that asymptotically, the speed-up is 1/α. In

the case of MoGo, this leads to α ≃ 0.05 and there-

fore roughly 20 as maximal speed-up for the case of a

tree simultaneously updated on all nodes. As commu-

nications are far from negligible, as preliminary ex-

periments were disappointing and as we expect better

than the 20 speed-up, we will not keep this algorithm

in the sequel.

THE PARALLELIZATION OF MONTE-CARLO PLANNING - Parallelization of MC-Planning

247

3.1 An Alternate Solution with Less

Communications

Section 3 showed that whenever communications are

perfect, the speed-up

is limited to some constant

1/α, roughly 20 in MoGo. We propose the follow-

ing algorithm (Algorithm 6), with the following ad-

vantages: (1) much less communications (can run on

usual ethernet); (2) tolerant to inhomogeneous nodes

(as other algorithms above also); (3) our implemen-

tation is not yet fault-tolerant, but it could be done;

(4) self-assessment possible (strong variance → more

time). The algorithm is detailed in Algorithm 6.

Algorithm 6: Algorithm for Monte-Carlo planning on a

cluster.

Initialize T to the root, representing the current state. T

is a tree of positions. T is the same on all computers.

for Each computer simultaneously: do

for Each thread simultaneously: do

while Time left > 0 do

Simulate one game until a node (=position) L of

T (thanks to bandit algorithms).

Choose one son L

′

of L.

Simulate one game from position L

′

until the

game is over.

Add L

′

as a son of L in T

Thread 0 only: if time −t0 ≥ T

, set t0 = time,

and average statistics in all the tree for nodes of

depth ≤ K with at least N

min

simulations.

end while

end for

Decision step:Pick up the decision which has been sim-

ulated most often, on the whole set of nodes.

An important advantage of this technique is that

averaging vectors of statistics is possible quickly on

a large number of nodes: the computational cost of

this averaging over N nodes is O(log(N)). The case

= ∞ in Algorithm 6 (no communication before the

ﬁnal step of the decision making) is just a form of

averaging. For computer-go, we get 59 %± 3% of

success rate with an averaging over 43 machines ver-

sus a single machine, whereas a speed-up 2 leads to

63%. This means that averaging provides a speed-up

less than 2 with 43 machines; this is not a good par-

allelization. We then experiment T

ﬁnite and K = 0

(i.e. only the root of the tree is shared between nodes):

This is not a ”real” speed-up, as the parallel algorithm,

even in the multi-core case, is not equivalent to the sequen-

tial one - the difference is the ”delay” detailed in section 2.

We here consider that the speed-up is k if the parallel algo-

rithm is as efﬁcient as the sequential one with k times more

time.

Number T

(time Success Estimated

N of between rate Speed-up

nodes updates) divided

by N

3 1.00s 67.2 ± 3.5 0.95 (9x9)

3 0.11s 67.3 ± 2.1 0.94 (9x9

4 0.33s 69.6 ± 1.5 0.81 (9x9)

9 0.33s 79.0 ± 1.0 (9x9)

9 0.11s 83.8 ± 5.4 (19x19)

We have no estimate for the 9-machines speed-

up, because comparing computational budget B with

9 machines and 9B with 1 machine implies the use

of games with average time per move 5.B, which re-

quires a lot of computational power. However, the

83.8% is in the extrapolation of linear speed-up. The

results were not signiﬁcantly different with higher

numbers of levels. We guess that for larger numbers

of nodes the results will be different but we have not

yet any empirical evidence of this.

4 CONCLUSIONS

Computer-Go is both a main target for computer-

games, as the main unsolved game, and a challeng-

ing planiﬁcation problem as the most promising ap-

proaches have a moderate expert knowledge and are

therefore quite general. In particular, successful ap-

plications of the UCT approach have been reported

very far from computer-Go (Kocsis and Szepesvari,

2006a). A main advantage of the approach is that it is

fully scalable. Whereas many expert-based tools have

roughly the same efﬁciency when doubling the com-

putational power, bandit-based Monte-Carlo planning

with time 2B has success rate roughly 63% against

a bandit-based Monte-Carlo planning algorithm with

time B. This leads to the hope of designing a paral-

lel platform, for an algorithm that would be efﬁcient

in various tasks of planiﬁcations. The main results in

this paper are the followings:

- Doubling the computational power (doubling the

time per move) leads to a 63% success rate against

the non-doubled version.

- The straightforward parallelization on a cluster (im-

itating the multi-core case by updating continuously

the trees in each node so that the memory is roughly

the same in all nodes) does not work in practice and

has strong theoretical limitations, even if all compu-

tational costs are neglected.

- A simple algorithm, based on averages which are

easily computable with classical message passing li-

braries, a few times per second, can lead to a great

successes; in 19x19, we have reached, with 9 nodes,

84 % success rate against one equivalent node. This

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

248

success rate is far above simple voting schemas, sug-

gesting that communications between independent

randomized agents are important and that communi-

cating only at the very end is not enough.

- Our two parallelizations (multi-core and cluster) are

orthogonal, in the sense that: (i) the multi-core paral-

lelization is based on a faster breadth-ﬁrst exploration

(the different cores are analyzing the same tree and go

through almost the same path in the tree; in spite of

many trials, we have no improvement by introducing

deterministic or random diversiﬁcation in the differ-

ent threads. (ii) the cluster parallelization is based

on sharing statistics guiding the ﬁrst levels only of

the tree, leading to a natural form of load balancing.

The deep exploration of nodes is completely orthog-

onal. Moreover, the results are cumulative; we see

the same speed-up for the cluster parallelization with

multi-threaded versions of the code or mono-thread

versions.

- In 9x9 Go, we have roughly linear speed-up until

4 cores or 9 nodes. The speed-up is not negligible

beyond this limit, but not linear. In 19x19 Go, the

speed-up remains linear until at least 4 cores and 9

machines.

Extending these results to higher numbers of ma-

chines is the natural further work. Increasing the

number of cores is difﬁcult, as getting an access to a

16-cores machine is not easy. Monte-Carlo planning

is a strongly innovative tool with more and more ap-

plications, in particular in cases in which variants of

backwards dynamic programming do not work. Ex-

trapolating the results to the human scale of perfor-

mance is difﬁcult. People usually consider that dou-

bling the computational power is roughly equivalent

to adding almost one stone to the level. This is con-

ﬁrmed by our experiments. Then, from the 2nd or 3rd

Kyu of the sequential MoGo in 19x19, we need 10 or

12 stones for the best human level. Then, we need

a speed-up of a few thousands. This is far from im-

possible, if the speed-up remains close to linear with

more nodes.

REFERENCES

Agrawal, R. (1995). The continuum-armed bandit problem.

SIAM J. Control Optim., 33(6):1926–1951.

Auer, P., Cesa-Bianchi, N., and Gentile, C. (2001). Adap-

tive and self-conﬁdent on-line learning algorithms.

Machine Learning Journal.

Banks, J. S. and Sundaram, R. K. (1992). Denumerable-

armed bandits. Econometrica, 60(5):1071–96. Avail-

able at http://ideas.repec.org/a/ecm/emetrp/

v60y1992i5p1071-96.html.

Barto, A., Bradtke, S., and Singh, S. (1993). Learning to

act using real-time dynamic programming. Technical

Report UM-CS-1993-002.

Bellman, R. (1957). Dynamic Programming. Princeton

Univ. Press.

Berry, D. A., Chen, R. W., Zame, A., Heath, D. C., and

Shepp, L. A. (1997). Bandit problems with inﬁnitely

many arms. Ann. Statist., 25(5):2103–2116.

Bertsekas, D. (1995). Dynamic Programming and Optimal

Control, vols I and II. Athena Scientiﬁc.

Bruegmann, B. (1993). Monte carlo go. Unpublished.

Cazenave, T. and Helmstetter, B. (2005). Combining tacti-

cal search and monte-carlo in the game of go. IEEE

CIG 2005, pages 171–175.

Coquelin, P.-A. and Munos, R. (2007). Bandit algorithms

for tree search. In Proceedings of UAI’07.

Coulom, R. (2006). Efﬁcient selectivity and backup opera-

tors in monte-carlo tree search. In P. Ciancarini and

H. J. van den Herik, editors, Proceedings of the 5th

International Conference on Computers and Games,

Turin, Italy.

Coulom, R. (2007). Computing elo ratings of move patterns

in the game of go. In van den Herik, H. J., Uiterwijk,

J. W. H. M., Winands, M., and Schadd, M., editors,

Computer Games Workshop, Amsterdam.

Dani, V. and Hayes, T. P. (2006). Robbing the bandit:

less regret in online geometric optimization against

an adaptive adversary. In SODA ’06: Proceedings

of the seventeenth annual ACM-SIAM symposium on

Discrete algorithm, pages 937–943, New York, NY,

USA. ACM Press.

Gelly, S. and Silver, D. (2007). Combining online and

ofﬂine knowledge in uct. In ICML ’07: Proceed-

ings of the 24th international conference on Machine

learning, pages 273–280, New York, NY, USA. ACM

Press.

Hussain, Z., Auer, P., Cesa-Bianchi, N., Newnham, L., and

Shawe-Taylor, J. (2006). Exploration vs. exploitation

challenge. Pascal Network of Excellence.

Kocsis, L. and Szepesvari, C. (2005). Reduced-variance

payoff estimation in adversarial bandit problems. In

Proceedings of the ECML-2005 Workshop on Rein-

forcement Learning in Non-Stationary Environments.

Kocsis, L. and Szepesvari, C. (2006a). Bandit-based monte-

carlo planning. ECML’06.

Kocsis, L. and Szepesvari, C. (2006b). Discounted-ucb. In

2nd Pascal-Challenge Workshop.

Lai, T. and Robbins, H. (1985). Asymptotically efﬁcient

adaptive allocation rules. Advances in Applied Math-

ematics, 6:4–22.

Powell, W.-B. (2007). Approximate Dynamic Program-

ming. Wiley.

Wang, Y. and Gelly, S. (2007). Modiﬁcations of UCT and

sequence-like simulations for Monte-Carlo Go. In

IEEE Symposium on Computational Intelligence and

Games, Honolulu, Hawaii, pages 175–182.

THE PARALLELIZATION OF MONTE-CARLO PLANNING - Parallelization of MC-Planning

249