LOCAL SEARCH AS A FIXED POINT OF FUNCTIONS

Eric Monfroy, Fr´ed´eric Saubion

University of Nantes, University of Angers, France

Broderick Crawford, Carlos Castro

Pontiﬁcia Universidad Cat´olica de Valpara´ıso, Universidad T´ecnica Federico Santa Mar´ıa, Valpara´ıso, Chile

Keywords:

Constraint Satisfaction Problems (CSP), Local Search, Constraint Solving.

Abstract:

Constraint Satisfaction Problems (CSP) provide a general framework for modeling many practical applica-

tions (planning, scheduling, time tabling, ...). CSPs can be solved with complete methods (e.g., constraint

propagation), or incomplete methods (e.g., local search). Although there are some frameworks to formalize

constraint propagation, there are only few studies of theoretical frameworks for local search. Here we are

concerned with the design and use of a generic framework to model local search as the computation of a ﬁxed

point of functions.

1 INTRODUCTION

A Constraint Satisfaction Problems (CSP) (Tsang,

1993) is usually deﬁned by a set of variables asso-

ciated to domains of possible values and by a set of

constraints. We only consider here CSP over ﬁnite

domains. Constraints can be understood as relations

over some variables and therefore,solving a CSP con-

sists in ﬁnding tuples that belong to each constraint

(an assignment of values to the variables that satisﬁes

these constraints).

From a practical point of view, CSP can be solved

by using either complete (such as constraint propaga-

tion (Apt, 2003)) or incomplete techniques (such as

local search (Aarts and Lenstra, 1997) or genetic algo-

rithms (Holland,1975)). Therefore, constraintsolvers

mainly rely on the implementation and combination

of these techniques. Local search techniques (Aarts

and Lenstra, 1997) have been successfully applied to

various combinatorial optimization problems.

In the CSP solving context, local search algo-

rithms are used either as the main resolution tech-

nique or in cooperation with other resolution pro-

cesses (e.g., constraint propagation) (Focacci et al.,

2002; Jussien and Lhomme, 2002). Unfortunately,

the deﬁnitions and the behaviors of these algorithms

are often strongly related to speciﬁc implementations

and problems. Our purpose is to use a framework

based on functions to provide uniform modeling tools

which could help better understanding local search al-

gorithms and designing new ones.

From a more conceptual and theoretical point of

view, K.R. Apt has proposed a mathematical frame-

work (Apt, 1997; Apt, 2003) for iteration of a ﬁnite

set of functions over “abstract” domains with partial

ordering: this is well-suited for solving CSPs with

constraint propagation.

To obtain a ﬁner deﬁnition of local search, in

(Monfroy et al., 2008) we proposed a computation

structure (the domain of Apt’s iterations)which is bet-

ter suited for local search. We deﬁned the basic func-

tions that can be used iteratively on this structure to

create a local search process. We identiﬁed the basic

processes used for intensiﬁcation and diversiﬁcation

(move and neighborhood computation) and the pro-

cess for jumping to other parts of the search space

(restart). These three processes are abstracted at the

same level by some homogeneous functions called re-

duction functions. The result of local search is then

computedas a ﬁxed point of this set of functions. Pos-

sible uses of this framework are illustrated through

the description of existing strategies such as descent

algorithms (WalkSat) and tabu search (Jaumard et al.,

1996).

431

Monfroy E., Saubion F., Crawford B. and Castro C. (2008).

LOCAL SEARCH AS A FIXED POINT OF FUNCTIONS.

In Proceedings of the Tenth International Conference on Enterprise Information Systems - AIDSS, pages 431-434

DOI: 10.5220/0001681804310434

 SciTePress

2 SOLVING CSP WITH LOCAL

A CSP is a tuple (X,D,C) where X = {x

, ··· , x

} is a

set of variables taking their values in their respective

domains D = {D

, ··· , D

}. A constraint c ∈ C is a

relation c ⊆ D

× · ·· × D

. In order to simplify no-

tations, D will also denote the Cartesian product of D

and C the union of its constraints. A tuple d ∈ D is a

solution of a CSP (X, D,C) if and only if ∀c ∈ C, d ∈ c.

In this paper, we always consider D ﬁnite.

For the resolution of a CSP (X, D,C), the search

space can be often deﬁned as the set of possible tu-

ples of D = D

× · ·· × D

and the neighborhood is a

mapping N : D → 2

This neighborhood function deﬁnes indeed the

possible moves from a sample (i.e., a tuple in this

case) to one of its neighbors and therefore fully de-

ﬁnes the exploration landscape. The ﬁtness (or eval-

uation) function eval is related to the notion of solu-

tion and can be deﬁned as the number of constraints c

that are not satisﬁed by the current sample, i.e., con-

straints such that d 6∈ c (d being the currently visited

sample, i.e., an element of D in this case). The prob-

lem to solve is then a minimization problem. Given a

sample d ∈ D, two basic cases can be identiﬁed in or-

der to continue the exploration of D: Intensiﬁcation,

choose d

′

∈ N (d) such that eval(d

′

) < eval(d); Di-

versiﬁcation, choose any other neighbor d

′

. In order

to integrate possiblerestarts (to start new paths) and to

generalize this approach we will consider local search

as a set of basic local searches.

3 LOCAL SEARCH AS A FIXED

POINT OF REDUCTION

FUNCTIONS

Local search acts usually on a structure which cor-

responds to points of the search space. In (Monfroy

et al., 2008) we propose a more general and abstract

deﬁnition based on the notion of sample, already sug-

gested. In our framework, local search is described as

a ﬁxed point computation.

For simplicity, we consider that each constraint is

over all the variables x

, . . ., x

. However, one can con-

sider constraints over some of the x

. Then, the notion of

scheme (Apt, 2003) can be used to denote sequences of vari-

ables.

3.1 Chaotic Iterations

K.R. Apt proposed chaotic iterations (Apt, 2003), a

general theoretical framework for computing limits of

iterations of a ﬁnite set of functions over a partially

ordered set. In this paper, we do not recall all the

theoretical results of K.R. Apt, but we just give the

GI algorithm for computing ﬁxed point of functions.

Consider a ﬁnite set F of functions, and d an element

of a partially ordered set D .

GI: Generic Iteration Algorithm.

d :=⊥;

G := F;

While G 6=

0 do

choose g ∈ G;

G := G− {g};

G := G∪ update(G, g,d);

d := g(d);

where ⊥ is the least element of the partial ordering

(D , ⊑), G is the current set of functions still to be

applied (G ⊆ F), and for all G,g, d the set of functions

update(G, g, d) from F is such that:

P1 { f ∈ F − G | f(d) = d ∧ f(g(d)) 6= g(d)} ⊆

update(G, g, d).

P2 g(d) = d implies that update(G, g,d) =

P3 g(g(d)) 6= g(d) implies that g ∈ update(G, g, d)

Suppose that all functions in F are reduction func-

tions as deﬁned before and that (D , ⊑) is ﬁnite (note

that ﬁniteness is important as is has already been men-

tioned for our structure). Then, every execution of the

GI algorithm terminates and computes in d the least

common ﬁxed point of the functions from F. We now

use the GI algorithm to compute the ﬁxed point of our

functions. The algorithm is thus feed with: a) a set

of fair restart functions, fair move and neighborhood

functions, that compose the set F; b) initial instanti-

ation of d, and c) the ordering that we use is the or-

dering ⊑. Unfortunately,the properties P1, P2 and P3

required in (Apt, 2003) for the update functions (to

insure the computation of the ﬁxed point) do not ﬁt

our extended functions. Indeed, our extended func-

tions are not deterministic and can modify a whole

local search even if a previous application did not.

This is due to the fact that the select function may

choose a conﬁguration which may not be modiﬁed by

a move (or a neighborhood) function whereas another

conﬁguration would be modiﬁed by the same move

(or neighborhood) function. However, remember the

fairness property of the select function: if one con-

ﬁguration can be changed by a move (or neighbor)

function, then this conﬁguration will not be neglected

forever; and a sample will not be neglected forever by

ICEIS 2008 - International Conference on Enterprise Information Systems

432

a restart function. Informally, the declarative deﬁni-

tion of the update means:

P1 put in the update(G, g,d) all functions not cur-

rently in G that will modifyg(d). This insures that

all effective functions will be re-applied (correct-

ness of the algorithm), whereas ineffective func-

tions will not be added (efﬁciency reasons).

P2 to ensure termination.

P3 to add g again if it must be re-used.

The update must satisfy the following properties:

P’1 { f ∈ F − G | ∀ f(d) = d ∧ ∃ f(g(d)) 6= g(d)} ⊆

update(G, g, d).

P’2 ∀g(d) = d implies that update(G, g, d) =

P’3 ∃g(g(d)) 6= g(d) implies that g ∈ update(G, g, d)

Basically, we need to put in the update set of

functions, functions that potentially will modify d,

the current whole local search. In these conditions,

the algorithm terminates and computes the least com-

mon ﬁxed point of the functions from F, i.e., the

result of the whole local search. Inspired by (Apt,

2003), the proof partially relies on an invariant ∀ f ∈

F − G, f(d) = d of the “while” loop in the algorithm.

This invariant is preserved by our characterization of

the update function (P’1, P’2 and P’3). Moreover,

since we keep a ﬁnite partial ordering and a set of

monotonic and inﬂationary functions, the results of

K.R. Apt can be extended here.

4 EXPERIMENTATION

The Sudoku problem consists in ﬁlling a 9 × 9 grid

so that every row, every column, and every 3× 3 box

contains the digits from 1 to 9. Although Sudoku,

when generalized to n

x n

grids to be ﬁlled in by

numbers from 1 to n

is NP-complete, the popular

9 × 9 grid with 3 × 3 regions is not difﬁcult to solve

with a computer program. Therefore, in order to in-

crease the difﬁculty, we consider 16× 16 grids (pub-

lished under the name ”super Sudoku”), 25 × 25 and

36 × 36 grids. On this problem, we will show that

our generic framework allows us to easily deﬁne local

search algorithms and to combine and compare them.

4.1 CSP Model

Consider a n

x n

problem, an instinctive formaliza-

tion consider a set of n

variables whose correspond,

to all the cells to ﬁll in. Using this, the set of related

constraints is deﬁned by AllDiff global contraints rep-

resenting: a) all digits appears only once in each row,

b) once in each column and c) once in each n × n

square the grid has been subdivided. Concerning LS

methods we focus on Tabu search (TS) (Glover and

Laguna, 1997). Basically, this algorithm forbidsmov-

ing to a sample that was visited less than l steps be-

fore. To this end, the list of the last l visited sam-

ples is memorized. On the other hand, we consider

a basic descent technique with random walks (RW)

where random moves are performed according to a

certain probability p. According to our model, we

only have now to design functions of the generic al-

gorithm of Section 3.1 to model strategies. Neigh-

bodhood functions are functions C → C such that

(p,V) 7→ (p,V ∪V

′

) with different conditions:

FullNeighbor : V

′

= {s ∈ D|s 6∈ V}

TabuNeighbor : V

′

= {s ∈ D| 6 ∃k,

n− l ≤ k ≤ n, s

= s}

DescentNeighbor : p = (s

, . . . , s

) and

′

= s ⊂ D s.t. 6 ∃s

′

∈ V

s.t. eval(s

′

) < eval(s

)

Move functions are functions C → C

s.t. (p,V) 7→ (p

′

0) with various conditions:

BestMove : p

′

= p⊕ s

′

and

eval(s

′

) = min

′′

∈V

eval(s

′′

ImproveMove : p = p

′′

⊕ s

and

′

= p⊕ s s.t. eval(s

′

) < eval(s

RandomMove : p

′

= p⊕ s

′

and s

′

∈ V.

We can precise here the input set of function F for

algorithm GI:

Tabusearch : {TabuNeighbor

;BestNeighBor}

Randomwalk : {FullNeighbor

;BestNeighBor;

RandomNeighbor}

TabuSearch+ Descent : {TabuNeighbor

;DescentNeighbor

;ImproveNeighBor

;BestNeighBor}

Randomwalk+ Descent : {FullNeighbor

;BestNeighBor

;RandomNeighbor

;DescentNeighbor

;ImproveNeighBor}

The different algorithms correspond to different

sets of input functions and different behaviours of

the choose function in the GI algorithm. choose

alternatively selects neighborhood and move func-

tions. For the Random Walk algorithm, given a prob-

ability parameter p, we have to introduce a quota

of p BestMove functions and 1 − p RandomMove

LOCAL SEARCH AS A FIXED POINT OF FUNCTIONS

433

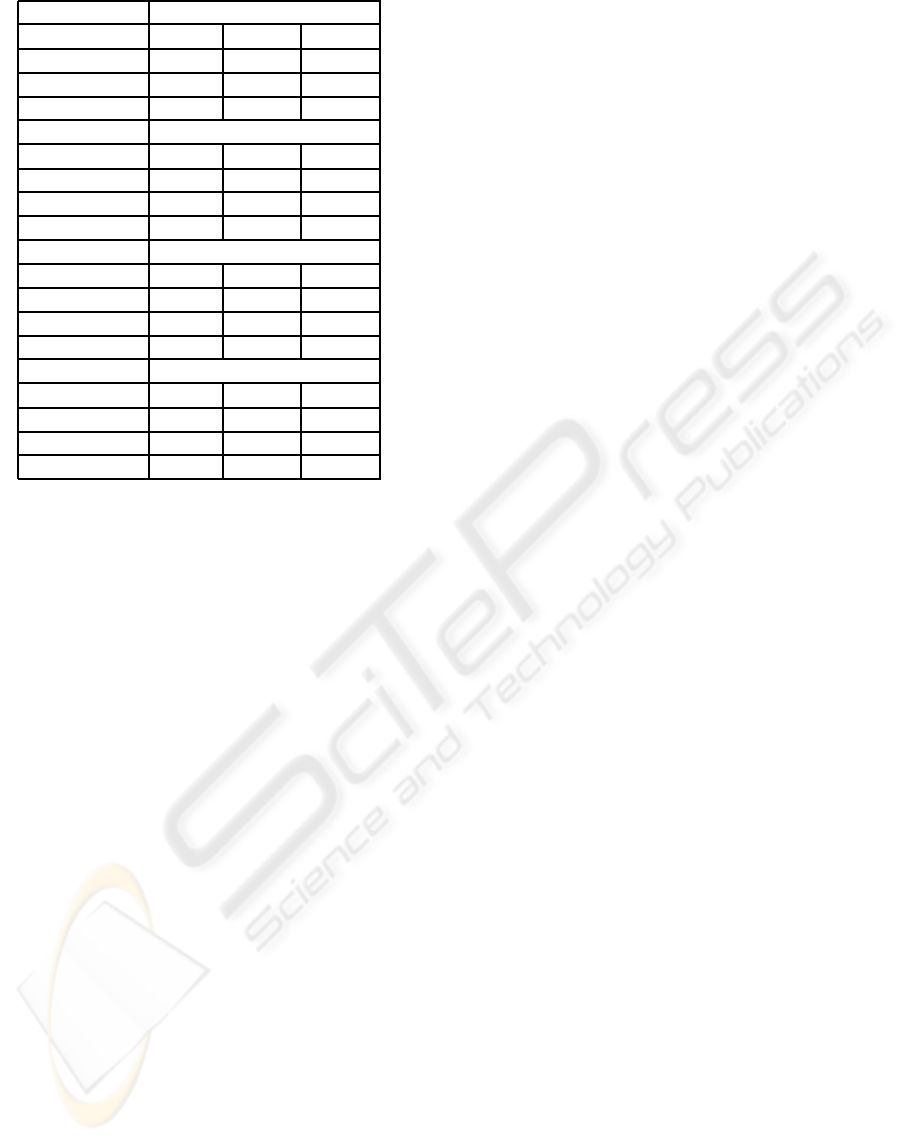
TabuSearch

x n

16x16 25x25 36x36

cpu time Avg 3,14 115,08 3289,8

deviations 1,28 52,3 1347,4

mvts Avg 405 3240 22333

RandomWalk

x n

16x16 25x25 36x36

cpu time Avg 3,92 105,22 2495

deviations 1,47 49,3 1099

mvts Avg 443 2318 13975

Descent + TabuSearch

x n

16x16 25x25 36x36

cpu time Avg 2,34 111,81

deviations 1,42 55,04

mvts Avg 534 3666

Descent +RandomWalk

x n

16x16 25x25 36x36

cpu time Avg 2,41 82,94 2455

deviations 1,11 36,99 1092

mvts Avg 544 2581 14908

Figure 1: Results of Sudoku problem by different search

approaches.

used in GI. Concerning Tabu Search, we use here a

TabuNeighbor with l = 10 and BestMove functions

to built our Tabu Search algorithm. At last, we com-

bine a descent strategy by adding DescentNeighbor

and ImproveMove to the previous sets in order to de-

sign algorithms in which a Descent is ﬁrst applied in

order to reach more quickly a good conﬁguration.

4.2 Experimentation Results

In Fig. 1 we compare results of the tabu search and

random walks associated with descent on different

instances of Sudoku problem. We have evaluated

the difﬁculty of the problem with a classic com-

plete method (propagation and split): we obtained

a more than one day cpu time cost for a 36 × 36

grid. At the opposite, by a simple formalization of the

problem and thanks to a function application model,

we are able to reach a solution with classical local

search algorithms starting from an empty grid. For

each method and for each instance, 2000 runs were

performed (except for 36 × 36 problem, 500 runs).

Adding descent in a Tabu Search or in a Random

Walk method, allows us to reduce the computation

time to reach a solution. The hybrid strategies com-

bining several move and neighborhood functions pro-

vide better results.

5 CONCLUSIONS

In this paper, we have used a framework to model lo-

cal search as a ﬁxed point of functions for solving

Sudoku. This framework provides a computational

model inspired in the initial works of K.R. Apt (Apt,

2003). It helps us to ﬁner deﬁne the basic processes

of local search at a uniform description level and to

describe speciﬁc search strategies. This mathemati-

cal framework could be helpful for the design of new

local search algorithms, the improvement of existing

ones and their combinations. Our framework could

also be used for experimental studies as it provides a

uniform description framework for various methods

in an hybridization context.

REFERENCES

Aarts, E. and Lenstra, J. K., editors (1997). Local Search

in Combinatorial Optimization. John Wiley & Sons,

Inc., New York, NY, USA.

Apt, K. R. (1997). From chaotic iteration to constraint prop-

agation. In Degano, P., Gorrieri, R., and Marchetti-

Spaccamela, A., editors, ICALP, volume 1256 of

Lecture Notes in Computer Science, pages 36–55.

Springer.

Apt, K. R. (2003). Principles of Constraint Programming.

Cambridge Univ. Press.

Focacci, F., Laburthe, F., and Lodi, A., editors (2002). Lo-

cal Search and Constraint Programming. In F. Glover

and G. Kochenberger, editors, Handbook of Meta-

heuristics, volume 57 of International Series in Op-

erations Research and Management Science. Kluwer

Academic Publishers, Norwell, MA.

Glover, F. and Laguna, F. (1997). Tabu Search. Kluwer

Academic Publishers, Norwell, MA, USA.

Holland, J. H. (1975). Adaptation in Natural and Artiﬁcial

Systems. University of Michigan Press.

Jaumard, B., Stan, M., and Desrosiers, J. (1996). Tabu

search and a quadratic relaxation for the satisﬁabil-

ity problem. DIMACS Series in Discrete Mathematics

and Theoretical Computer Science, 26:457–478.

Jussien, N. and Lhomme, O. (2002). Local search with con-

straint propagation and conﬂict-based heuristics. Artif.

Intell., 139(1):21–45.

Monfroy, E., Saubion, F., Crawford, B., and Castro, C.

(2008). Towards a formalization of combinatorial

local search. In Proceedings of the International

MultiConference of Engineers and Computer Scien-

tists, IMECS, March 19-21, 2008, Hong Kong, China,

Lecture Notes in Engineering and Computer Science.

Newswood Limited.

Tsang, E. (1993). Foundations of Constraint Satisfaction.

Academic Press, London.

ICEIS 2008 - International Conference on Enterprise Information Systems

434