AN APPROXIMATE PROPAGATION ALGORITHM FOR
PRODUCT-BASED POSSIBILISTIC NETWORKS
Amen Ajroud, Mohamed Nazih Omri
FSM, Universit´e de Monastir, Boulevard de l’Environnement 5019, Monastir, Tunisia
Salem Benferhat
CRIL, Universit´e d’Artois, Rue Jean Souvraz SP18, 62300, Lens, France
Habib Youssef
ISITCOM, Universit´e de Sousse, Route principale n
◦
1, 4011, Hammam Sousse, Tunisia
Keywords:
Possibilistic networks, possibility distributions, approximate inference, DAG multiply connected.
Abstract:
Product-Based Possibilistic Networks appear to be important tools to efficiently and compactly represent pos-
sibility distributions. The inference process is a crucial task to propagate information into network when new
pieces of information, called evidence, are observed. However, this inference process is known to be a hard
task especially for multiply connected networks. In this paper, we propose an approximate algorithm for
product-based possibilistic networks. More precisely, we propose an adaptation of the probabilistic approach
“Loopy Belief Propagation” (LBP) for possibilistic networks.
1 INTRODUCTION
Graphical models are important tools to efficiently
represent and analyze uncertain information. Among
these graphical representations, Bayesian Networks
are particulary well defined and well applied. Possi-
bilistic networks appear to be an alternative approach
to model both uncertainty and imprecision. There
are two kinds of possibilistic networks: Min-Based
Possibilistic Networks and Product-Based Possibilis-
tic Networks (Fonck, 1994). These two kinds of pos-
sibilistic networks only differ on the definition of pos-
sibilistic conditioning.
One of the most critical issue in probabilistic and
possibilistic networks is the propagation of informa-
tion through the graph structure. Unfortunately, it is
known that both probabilistic an possibilistic infer-
ence are hard tasks specially when graphs are mul-
tiply connected (Cooper, 1990) and (Dagum & Luby,
1993). Indeed, when the networks are simply con-
nected, the propagation of possibility degrees is not
very difficult and can be achieved in a polynomial
time. When the networks are large and multiply con-
nected, several problems emerge: the inference re-
quires an enormous memory size and calculation be-
comes complex and even impossible.
The inference algorithms can be classified in two
categories (Guo & Hsu, 2002):
• Exact algorithms: these methods mostly ex-
ploit the independencies relations present in the
network and transform the initial graph into a
new graphical structure such that a junction tree.
These algorithms give the exact posterior possi-
bility degree.
• Approximate algorithms: they are alternatives of
exact algorithms when the networks become very
complex. They estimate the posterior uncertain
degree in various ways.
In possibility theory frameworks, Exact algo-
rithms have been defined for both min-based and
product-based graphs. Moreover, an anytime approxi-
mate algorithm has been proposed for min-based pos-
sibilistic networks (Ben Amor & al, 2003). However,
to the best of our knowledge, no approximate algo-
rithm exists for product-based possibilistic networks.
In this paper we focus on product-based possi-
bilistic network and propose a possibilistic inference
algorithm which allows to determine an approxima-
tion of possibility degree of any variable of interest
given some evidence. This possibilistic algorithm is
an adaptation of a well-known probabilistic algorithm
321
Ajroud A., Nazih Omri M., Benferhat S. and Youssef H. (2008).
AN APPROXIMATE PROPAGATION ALGORITHM FOR PRODUCT-BASED POSSIBILISTIC NETWORKS.
In Proceedings of the Tenth International Conference on Enterprise Information Systems - AIDSS, pages 321-326
DOI: 10.5220/0001711403210326
Copyright
c
 SciTePress

“Loopy Belief Propagation” (Murphy & al, 1999) and
(Bishop, 2006). Conditions for exact inference in
multiply connected graphs through LBP have been
demonstrated (Heskes, 2003). Without any transfor-
mation of the initial graph, the basic idea of this adap-
tation is to propagate evidence into network by pass-
ing messages between nodes. More precisely, mes-
sages are exchanged between each node and its par-
ents and its children. We keep passing messages in
the network until a stable state is reached (if ever).
The rest of this paper is organized as follows:
first, we give a brief background on possibility the-
ory and product-based possibilistic networks (section
2). Then, we present our possibilistic adaptation of
“Loopy Belief Propagation” algorithm for product-
based possibilistic networks (Section 3). Section 4
gives some experimental results.
2 POSSIBILITY THEORY AND
POSSIBILISTIC NETWORKS
This section presents a short summary of Possibility
Theory; for more details see (Dubois & Prade, 1988).
Let V = {A
1
, A
2
, ..., A
n
} be a set of variables. We
denote by D
A
i
the finite domain associated with the
variable A
i
. a
i
denotes any instance of variable A
i
.
Ω = ×
A
i
∈V
D
A
i
represents the universe of dis-
course and ω, an element of Ω, is called an interpre-
tation or state. The tuple (α
1
, α
2
, ..., α
n
) denotes the
interpretation ω, where each α
i
is an instance of A
i
.
2.1 Possibility Distribution
A possibility distribution π is a mapping from Ω to the
interval [0, 1]. The degree π(ω) represents the com-
patibility of ω with available piece of information. In
other words, if π is used as an imperfect specification
of a current state ω
0
of a part of the world, then π(ω)
quantifies the degree of possibility that the proposi-
tion ω = ω
0
is true. By convention, π(ω) = 0 means
that ω = ω
0
is impossible, and π(ω) = 1 means that
this proposition is regarded as being possible with-
out restriction. Any intermediary possibility degree
π(ω) ∈]0, 1[ indicates that ω = ω
0
is somewhat possi-
ble. A possibility distribution π is said to be normal-
ized if there exists at least one state which is consis-
tent with available pieces of information. More for-
mally,
∃ω ∈ Ω, such that π(ω) = 1.
Given a possibility distribution π defined on Ω, we
can define a mapping grading the possibility measure
of an event ϕ ⊆ Ω to the interval [0, 1] by,
Π(ϕ) = max{π(ω) : ω ∈ ϕ}.
Possibilistic conditioning (Dubois & Prade, 1988)
consists in modifying our initial knowledge, encoded
by a possibility distribution π, by the arrival of a new
piece of information ϕ ⊆ Ω. We will focus only on
product-based conditioning, defined by:
π(ω|ϕ) =
(
π(ω)
Π(ϕ)
if ω ∈ ϕ
0 otherwise
2.2 Product-based Possibilistic
Networks
Possibilistic networks (Fonck, 1994), (Borgelt &
al,1998), (Gebhardt & Kruse, 1997) and (Kruse &
Gebhardt, 2005), denoted by ΠG, are directed acyclic
graphs (DAG). Nodes correspond to variables and
edges encode relationships between variables. A node
A
j
is said to be a parent of A
i
if there exists an edge
from the node A
j
to the node A
i
. Parents of A
i
are
denoted by U
A
i
.
Uncertainty is represented at each node by local
conditional possibility distributions. More precisely,
for each variable A:
If A is a root, namely U
A
=
/
0, then
max(π(a
1
), π(a
2
)) = 1.
If A has parents, namely U
A
6=
/
0, then
max(π(a
1
|U
A
), π(a
2
|U
A
)) = 1, for each u
A
∈ D
U
A
,
where D
U
A
is the domain of parents of A.
Possibilistic networks are also compact represen-
tations of possibility distributions. More precisely,
joint possibility distributions associated with possi-
bilistic networks are computed using a so-called pos-
sibilistic chain rule similar to the probabilistic one,
namely :
π
ΠG
(a
1
, ..., a
n
) =
∏
i=1..n
Π(a
i
| u
A
i
),
where a
i
is an instance of A
i
and u
A
i
∈ D
U
A
i
is an
instance of domain of parents of node A
i
.
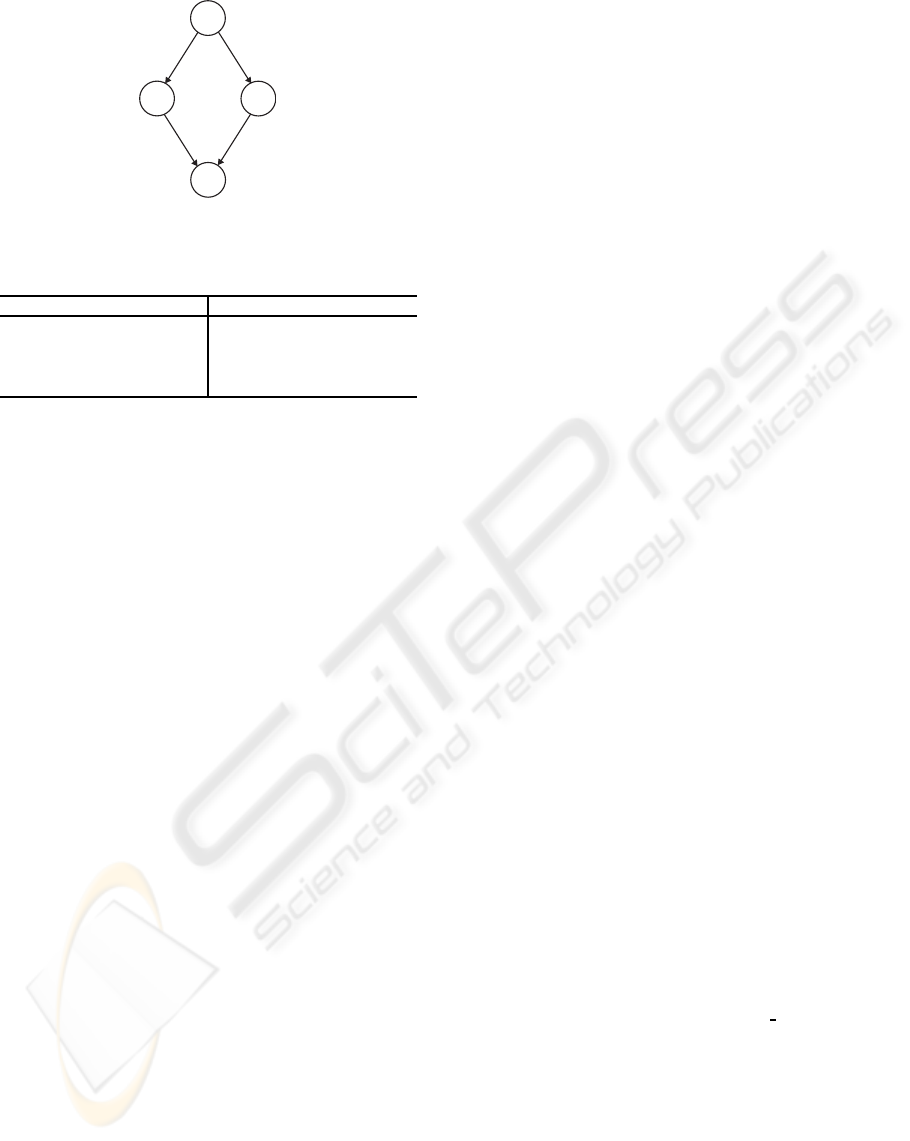
Example 1. Figure 1 gives an example of a possi-
bilistic network. Table 1 and 2 provide local condi-
tional possibility distributions of each node given its
parents.
Table 1: Initial possibility distributions.
a π(a) b a π(b|a) c a π(c|a)
a
1
0.3 b
1
a
1
1 c
1
a
1
0.2
a
2
1 b
1
a
2
0.4 c
1
a
2
1
b
2
a
1
0 c
2
a
1
1
b
2
a
2
1 c
2
a
2
0.3
ICEIS 2008 - International Conference on Enterprise Information Systems
322

A
B
C
D
Figure 1: Example of a multiply connected DAG.
Table 2: Initial possibility distributions.
d b c π(d|b, c) d b c π(d|b, c)
d
1
b
1
c
1
1 d
2
b
1
c
1
1
d
1
b
1
c
2
0 d
2
b
1
c
2
1
d
1
b
2
c
1
0.8 d
2
b
2
c
1
1
d
1
b
2
c
2
0.1 d
2
b
2
c
2
1
Using a possibilistic chain rule, we encode the joint
distribution relative to A, B, C and D as follows :
∀a, b, c, d π(a, b, c, d) = π(a).π(b|a).π(c|a).π(d|b, c).
For instance,
π(a
1
, b
1
, c
2
, d
2
) = π(a
1
).π(b
1
|a
1
).π(c
2
|a
1
).π(d
2
|b
1
, c
2
) =
0.3.1.1.1 = 0.3
3 ADAPTATION OF LBP FOR
POSSIBILISTIC NETWORKS
This section summarizes a direct adaptation of prob-
abilistic LBP algorithm in the possibilistic frame-
work. The probabilistic “Loopy Belief Propagation”
is an approximate inference algorithm which applies
the rules of Pearl Algorithm (Pearl, 1986) for mul-
tiply connected DAG. The basic idea of LBP is to
propagate evidence into network by passing messages
iteratively between nodes. We keep passing mes-
sages in the network until a stable state is reached
(if ever). LBP is still a good alternative for exact
inference methods specially when these latter meet
difficulties to run. Let Y
A
= {Y
1
,Y
2
, ..,Y
n
}, and U
A
=
{U
1
,U
2
, ..,U
m
} be respectively the set of children and
parents of node A.
With our adaptation, propagate an evidence E=e
into Product-Based possibilistic algorithm is resumed
to calculate the belief in a non-evidence node A,
which is approximatedby a conditional possibility de-
gree of A, formally:
∀a ∈ D
A
, Bel(a) = α.λ(a).µ(a) ≈ π(a | e), (1)
where α is a normalizing constant, λ(a) and µ(a) are
iteratively calculated.
At iteration t, λ
(t)
(a) and µ
(t)
(a) represent the in-
coming messages to node A received from, respec-
tively, children and parents of A:
λ
(t)
(a) = λ
A
(a).
n
∏
j=1
λ
(t)
Y
j
(a) (2)
µ
(t)
(a) = max
u
π(a|u).
m
∏
i=1
µ
(t)
A
(u
i
) (3)
At iteration t+1, the node A sends outgoing mes-
sages (λ-messages and µ-messages) to, respectively,
its parents and its children:
λ
(t+1)
A
(u
i
) = β max
a
λ
(t)
(a).[max
u
k:k6=i
π(a|u).
∏
k6=i
µ
(t)
A
(u
k
)]
(4)
µ
(t+1)
Y
j
(a) = γ λ
A
(a).
n
∏
i=1,i6= j
λ
(t)
Y
i
(a). µ
(t)
(a) (5)
Nodes are updated in parallel: at each iteration, all
nodes compute their outgoing messages based on the
input of their neighbors from the previous iteration.
This procedure is said to converge if none of the be-
liefs in successive iterations changed by more than a
small threshold (e.g. 10
−3
) (Murphy and al, 1999).
We note that these formulas are similar to those
corresponding to probabilistic framework but we use
the maximum operator instead of the addition. The
outline of our adaptation algorithm is as follows:
Algorithm: Product-Based possibilistic inference
in multiply connected DAG
BEGIN
N ← {nodes of network};
for all nodes, initialization of :
- λ
A
n
(a
n
) by 1 or its observed value;
- λ-messages and µ-messages by vector 1 ;
- Bel(a
m
) ← 0 ;
M ← {number of non-observed nodes};
t ← 1;
convergence ← FALSE;
while NOT convergence and t < max itr
for n ← 1 to length(N)
calculate λ
(t)
(a
n
) with the formula (2);
calculate µ
(t)
(a
n
) with the formula (3);
end
for m ∈ M
OldBel(a
m
) ← Bel(a
m
);
calculate Bel(a
m
) with the formula (1);
end
if ∀ m ∈ M, Bel(a
m
)−OldBel(a
m
) < tol
convergence ← TRUE;
AN APPROXIMATE PROPAGATION ALGORITHM FOR PRODUCT-BASED POSSIBILISTIC NETWORKS
323

end
if NOT convergence
for n ← 1 to length(N)
calculate for every parent U
i
of A
n
; λ
(t+1)
A
n
(u
i
)
with the formula (4);
calculate for every child Y
j
of A
n
; µ
(t+1)
Y
j
(a
n
)
with the formula (5);
end
t ← t + 1;
end
end
END
Example 2. Given the Product-Based possibilistic
network presented in Example 1, we now try to run
our possibilistic adaptation. For example, we ob-
serve, as evidence, the node D=d
2
and we compute,
progressively, possibility degree of each other node
knowing the evidence. Table 3 shows for each iter-
ation values obtained for A, B and C. Note that the
algorithm converges after 3 iterations. We indicate,
for comparison, the exact values given by an exact
inference algorithm.
Table 3: Posterior possibility degree.
iteration t = 1 t = 2 t = 3 exact values
π(a
1
| d
2
) 0.3 0.3 0.3 0.3
π(a
2
| d
2
) 1 1 1 1
π(b
1
| d
2
) 1 0.4 0.4 0.4
π(b
2
| d
2
) 1 1 1 1
π(c
1
| d
2
) 1 1 1 1
π(c
2
| d
2
) 1 0.3 0.3 0.3
4 EXPERIMENTAL RESULTS
The implementation of possibilistic adaptation of
LBP is based on the Bayes Net Toolbox (BNT) (Mur-
phy & al, 1999) which is an open source Matlab pack-
age for directed graphical models. We used also the
Possibilistic Networks Toolbox (PNT) which imple-
ments the exact inference algorithm : product-based
Junction Tree (Ben Amor, 2002). The experimenta-
tion is performed on random possibilistic networks
generated as follows:
Graphical Components. We used two DAGsstruc-
tures generated as follows:
• STRUCTURE 1: In the first structure, the DAGs
are multiply connected and generated randomly.
We fixed the total number of nodes at 30. The
cardinality of node instances is chosen randomly
between 2 and 3. We can also change the number
of parents for each node.
• STRUCTURE 2: In the second one, we choose
special cases of DAGs where nodes are parti-
tioned into two levels. This structure corresponds
to well-known networks as the QMR (Quick
Medical Reference) network (Jaakkola & Jordan,
1999). We have diseases level and findings level
and we try to infer the distribution of diseases
given a subset of findings. We chose specially this
kind of network because it is known that in many
cases, the probabilistic LBP did not converge to a
stable state. We generate randomly this structure
of graph with 30 nodes with instance cardinality
∈ {2, 3}.
Numerical Components. Once the DAG structure
is fixed, we generate random conditional distributions
of each node in the context of its parents. Then, we
generate randomly the variable of interest.
4.1 Convergence
In this first experimentation we propose to evaluate
the convergence of our approximate algorithm. Here,
we focus on the number of iterations needed for the
algorithm to converge. First, this experimentation is
performed on 1000 random networks from STRUC-
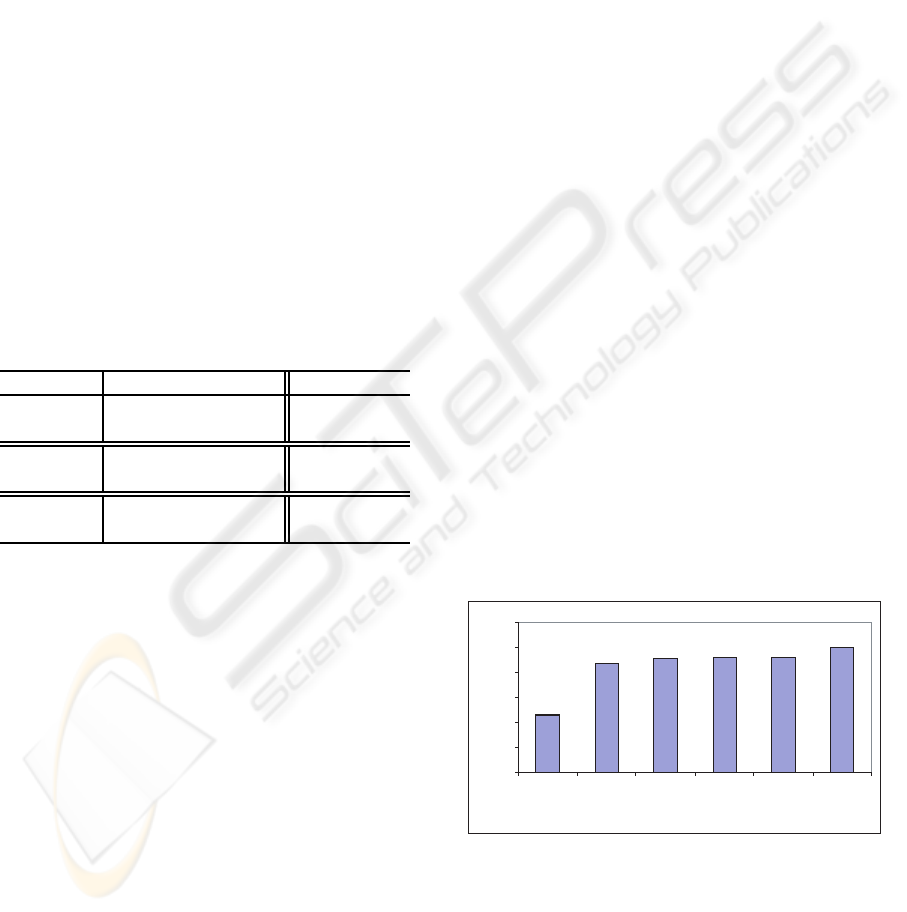
TURE 1. Figure 2 shows that 46% of random net-
works generated need less than 5 iterations to con-
verge. In the same way, 91% of networks gener-
ated need less than 20 iterations to reach convergence
state. We consider that it is a satisfactory result with
reasonable iterations number.
46%
87%
91%
92%
92%
100%
0%
20%
40%
60%
80%
100%
120%
<=5 <=10 <=20 <=50 <=100 >100
ite ration num ber
Figure 2: Iteration number for DAG of STRUCTURE 1.
We repeat the same experimentation with 1000
DAG having QMR structure (STRUCTURE 2). Fig-
ure 3 shows results of this experimentation. We note
that for less than 20 iterations 85% of random net-
works converge. This result is slightly inferior to
ICEIS 2008 - International Conference on Enterprise Information Systems
324

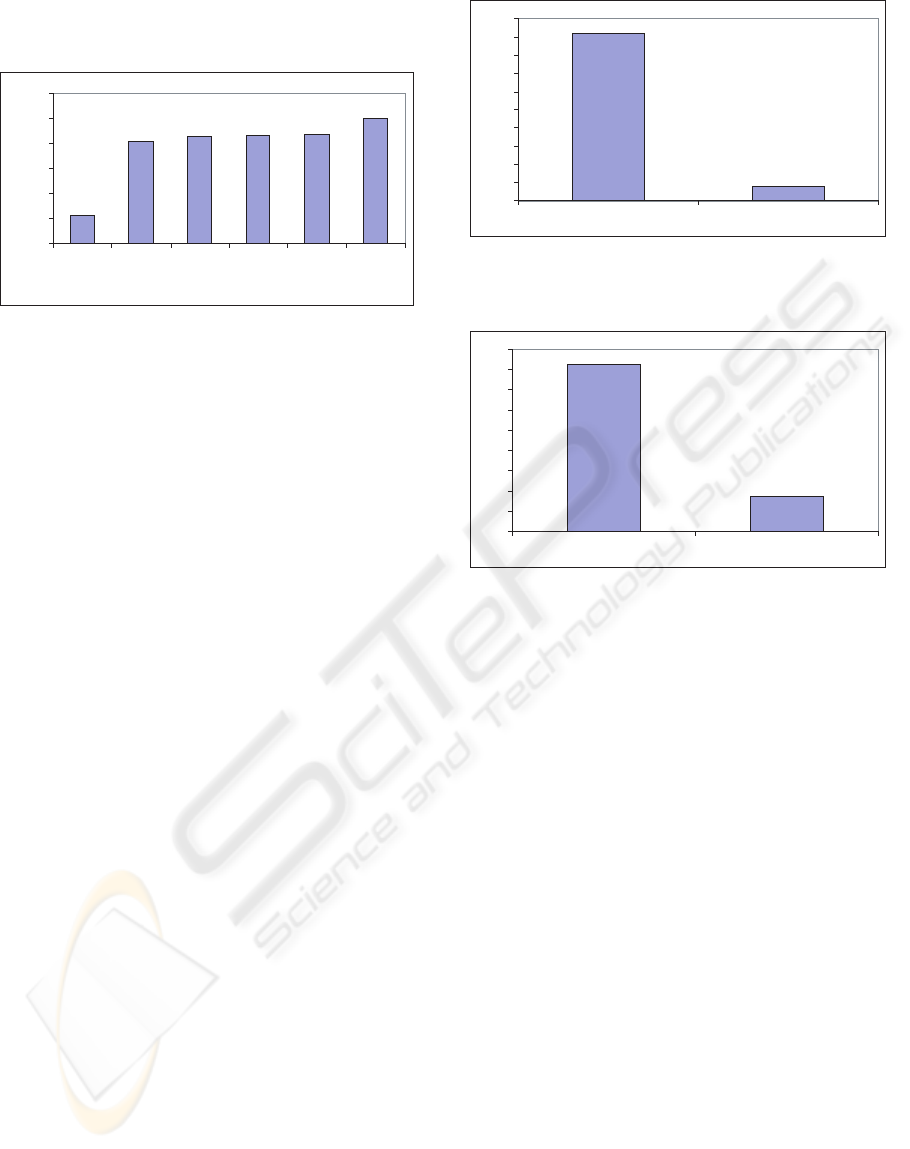
the first experimentation because QMR graph is less
likely to converge than other structures.
22%
81%
85%
86%
87%
100%
0%
20%
40%
60%
80%
100%
120%
<=5 <=10 <=20 <=50 <=100 >100
iteration number
Figure 3: Iteration number for QMR DAG.
4.2 Exactness
We are now interested in the exactness of values gen-
erated by the approximate algorithm. Here, we mea-
sure the difference between approximate and exact
values generated by respectively approximate and ex-
act inference algorithm. This difference between val-
ues expresses how much our algorithm can approx-
imate the exact one. More precisely, for one net-
work, we compute possibility degrees obtained by our
approximate algorithm and possibility degrees gener-
ated by an exact algorithm : the product-based junc-
tion tree algorithm (Ben Amor, 2002). Then we com-
pute, for each node of the graph, the difference be-
tween exact and approximate possibility degrees. We
consider that there is equality between 2 compared
values if the difference between them is less than a
fixed threshold (10
−2
). finally, we count the number
of equality and inequality cases and we obtain a per-
centage of each state.
Figure 4 summarizes the results of this experi-
mentation applied to 1000 random graphs generated
by STRUCTURE 1. 92% of numerical values issued
from approximate algorithm coincide with those is-
sued from exact algorithm. Note that here we did not
discard the samples of non-convergence.
Figure 5 represents the result of the same ex-
perimentation using 1000 QMR graphs generated by
STRUCTURE 2. In this case, only 83% of numerical
values issued from approximate algorithm are consid-
ered to be exact. The results of these statistics for the
two graph structures conclude that the approximate
possibility degrees are closed with exact possibility
degrees.
8%
92%
0%
10%
20%
30%
40%
50%
60%
70%
80%
90%
100%
exact inexact
Figure 4: Average of compared values in randomly graph
structure.
17%
83%
0%
10%
20%
30%
40%
50%
60%
70%
80%
90%
exact inexact
Figure 5: Average of compared values in QMR graph struc-
ture.
5 CONCLUSIONS
In this paper we proposed an approximate inference
algorithm for Product-Based Possibilistic networks.
It is an adaptation of probabilistic LBP algorithm in
possibilistic framework. Without any structure trans-
formation, the algorithm consists to propagate evi-
dence, into multiply connected network, by passing
messages between nodes. Our adaptation is an inter-
esting alternative implementation for exact inference
when this one fails on complex network (when sizes
of cliques are large). Experimental results show that
the possibility distributions generated by approximate
algorithm are very near to exact possibility distribu-
tions. In a future work, we project to apply this new
propagation algorithm by it’s adaptation to handling
interventions in possibilistic causal networks (Benfer-
hat & Smaoui, 2007).
REFERENCES
Ben Amor, N. (2002). Qualitative possibilistic graphical
models : from independence to propagation algo-
rithms. Th`ese de doctorat, Universit´e de Tunis, ISG.
AN APPROXIMATE PROPAGATION ALGORITHM FOR PRODUCT-BASED POSSIBILISTIC NETWORKS
325

Ben Amor, N., Benferhat, S., & Mellouli, K. (2003) Any-
time Propagation Algorithm for Min-based Possibilis-
tic Graphs. Soft Computing, A fusion of foundations,
methodologies and applications, 8, 150-161.
Benferhat, S., & Smaoui, S. (2007). Possibilistic Causal
Networks for Handling Interventions: A New Prop-
agation Algorithm. The Twenty-Second AAAI Confer-
ence on Artificial Intelligence (AAAI’07), pp.373-378.
Bishop, C. M., (2006). Pattern Recognition and Machine
Learning. Springer.
Borgelt, C., Gebhardt, J., & Kruse, R. (1998). Possibilis-
tic graphical models. Proceedings of International
School for the Synthesis of Expert Knowledge (IS-
SEK’98), pp.51-68.
Cooper, G. F. (1990). Computational complexity of proba-
bilistic inference using Bayesian belief networks. Ar-
tificial Intelligence, pp.393-405.
Dagum, P., & Luby, M. (1993). Approximating probabilis-
tic inference in Bayesian belief networks is NP-hard.
Artificial Intelligence, 60, 141-153.
Dubois, D., & Prade, H. (1988). Possibility theory : An
approach to computerized, Processing of uncertainty.
Plenium Press, New York.
Fonck, P. (1994). R´eseaux d’inf´erence pour le raisonnement
possibiliste. PhD thesis, Universit´e de Li`ege, Facult´e
des Sciences.
Gebhardt, J., & Kruse, R. (1997). Background and per-
spectives of possibilistic graphical models, Quali-
tative and Quantitative Practical Reasoning (EC-
SQARU/FAPR’97), pp.108-121.
Guo, H., & Hsu, W. (2002). A survey of algorithms for real-
time Bayesian network inference, Joint Workshop on
Real-Time Decision Support and Diagnosis Systems
(AAAI/KDD/UAI-2002), pp.1-12.
Heskes, T. (2003). Stable fixed points of loopy belief propa-
gation are minima of the Bethe free energy. Advances
in Neural Information Processing Systems, 15, 359-
366.
Jaakkola, T.S., & Jordan, M.I. (1999). Variational proba-
bilistic inference and the qmr dt network. Journal of
Artificial Intelligence Research, 10, 291-322.
Kruse, R., & Gebhardt, J. (2005). Probabilistic Graphical
Models in Complex Industrial Applications. Fifth In-
ternational Conference on Hybrid Intelligent Systems
(HIS’05), p.3.
Murphy, K. P., Weiss, Y., & Jordan, M. I. (1999). Loopy
belief propagation for approximate inference: An em-
pirical study. Proceedings of the Fifteenth Conference
on Uncertainty in Artificial Intelligence (UAI’99),
pp.467-475,
Pearl, J. (1986). Fusion, propagation and structuring in be-
lief networks. Artificial Intelligence, 29, 241-288.
ICEIS 2008 - International Conference on Enterprise Information Systems
326