Checking Inherently Fair Linear-Time Properties in a
Non-Na
¨
ıve Way
?
Thierry Nicola, Frank Nießner and Ulrich Ultes-Nitsche
Department of Computer Science, University of Fribourg
Boulevard de P
´
erolles 90, CH-1700 Fribourg, Switzerland
Abstract. In [9], an alternative verification relation for linear-time properties is
introduced which uses an inherent fairness condition. That relation is specifically
tailored to the verification of distributed systems under a relaxed version of strong
fairness. We will call it the inherently fair linear-time verification relation in this
paper, or IFLTV relation for short. We present an analysis of the mathematical
structure of the IFLTV relation, which enables us to obtain an improved non-
na
¨
ıve procedure for checking the IFLTV relation.
1 Introduction
The results of [9] yield an immediate procedure for checking the satisfaction of the
IFLTV relation on B
¨
uchi automata describing the behavior of a system and a linear-time
property, respectively. We refer to that procedure as the na
¨
ıve procedure. Even though
the IFLTV relation is practically applicable as it comes with an abstraction concept
based on so-called weakly continuation-closed abstractions [9], which can be computed
efficiently from trace reductions of the automaton representing the behavior [10, 12], the
na
¨
ıve procedure for checking the IFLTV relation is sub-optimal and somehow limiting
the applicability of the entire verification approach.
In this paper we analyze the IFLTV relation and apply the results to the structure
of the involved automaton representations of system behavior and property. By doing
so we define a procedure for checking IFLTV which requires fewer computation steps
than the na
¨
ıve one. This procedure is the main result of this paper and we will refer it
as being the non-na
¨
ıve procedure.
This paper is structured as follows: Sect. 2 gives a very brief motivation for the
definition of the IFLTV relation; more motivating information can be found in [9]. Af-
ter introducing some preliminary concepts in Sect. 3, we define in Sect. 4 the IFLTV
relation formally. In Sect. 5, the IFLTV relation is analyzed to the extent that we can
construct from it an IFLTV checking procedure for automaton representations of be-
havior and property in Sect. 6, analyzing its correctness in Sect. 7 and discussing its
complexity in Sect. 8. Finally Sect. 9 concludes the paper.
?
Supported by the Swiss National Science Foundation under grant # 200021-103985/1 and by
the Hasler Foundation under grant # 1922.
Nicola T., Nießner F. and Ultes-Nitsche U. (2008).
Checking Inherently Fair Linear-Time Properties in a Non-Näıve Way.
In Proceedings of the 6th International Workshop on Modelling, Simulation, Verification and Validation of Enterprise Information Systems, pages 49-58
DOI: 10.5220/0001736600490058
Copyright
c
 SciTePress

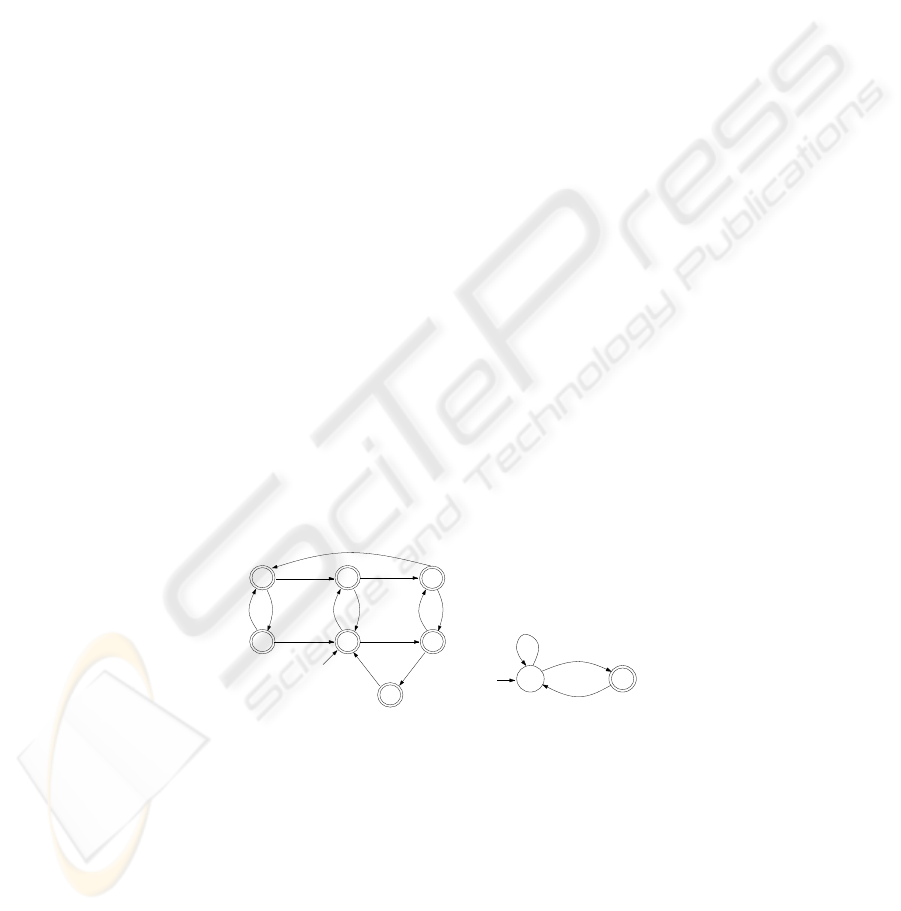
2 Motivation
Assume two systems, both randomly selecting initially an unbounded positive integer
n. The first system will operate n steps and then stop. The second system will either
operate n steps and stop, or may decide nondeterministically to operate forever. Only in-
finitely long observations could distinguish the two systems, which are apparently prac-
tically impossible. So, system one is as good as system two from the point of view of
an outside observer. Linear-time verification, however, distinguishes the two systems as
the second system does not satisfy the property ‘always performing only finitely many
operations’ where the first one does. Besides being insensitive to such differences re-
quiring infinite observations, IFLTV is as powerful as the usual linear-time verification
relation. The two verification relations coincide, for instance, in safety properties [9]
and differ only in liveness properties [2]. We consider IFLTV the more practical veri-
fication relation, as it is related to only those differences in system behavior which can
practically (in a finite amount of time) be observed.
Consider the following abstract model of a server, see Fig. 1a. If the server resource
is free, the server reacts to a request by an internal event yes, followed by sending
result, but if the resource is locked, then a request is rejected by the server. A desired
property of a server is that it eventually returns a result. This property can be expressed
by the automaton in Fig. 1b. However, our model does not satisfy this property using the
classical linear-time verification relation, see for instance [14, 13], because the model,
and any reasonable model of such a system, contains the extreme execution scenario
in which whenever a request is made the resource is locked. In our model, for instance
lock · (request · no · reject)
ω
is such a behavior violating the linear-time satisfaction
of the property. However, such a behavior is highly unfair, and such extreme executions
are normally ignored by using an explicit fairness assumption restricting the allowed
executions of the system. In our example assuming strong fairness [6] would do the
job. For linear-time satisfaction it is therefore necessary to add such an explicit fairness
condition.
2 Motivation
Assume two systems, both randomly selecting initially an unbounded positive integer
n. The first system will operate n steps and then stop. The second system will either
operate n steps and stop, or may decide nondeterministically to operate forever. Only in-
finitely long observations could distinguish the two systems, which are apparently prac-
tically impossible. So, system one is as good as system two from the point of view of
an outside observer. Linear-time verification, however, distinguishes the two systems as
the second system does not satisfy the property ‘always performing only finitely many
operations’ where the first one does. Besides being insensitive to such differences re-
quiring infinite observations, IFLTV is as powerful as the usual linear-time verification
relation. The two verification relations coincide, for instance, in safety properties [9]
and differ only in liveness properties [2]. We consider IFLTV the more practical veri-
fication relation, as it is related to only those differences in system behavior which can
practically (in a finite amount of time) be observed.
Consider the following abstract model of a server, see Fig. 1a. If the server resource
is free, the server reacts to a request by an internal event yes, followed by sending
result, but if the resource is locked, then a request is rejected by the server. A desired
property of a server is that it eventually returns a result. This property can be expressed
by the automaton in Fig. 1b. However, our model does not satisfy this property using the
classical linear-time verification relation, see for instance [14, 13], because the model,
and any reasonable model of such a system, contains the extreme execution scenario
in which whenever a request is made the resource is locked. In our model, for instance
lock · (request · no · reject)
ω
is such a behavior violating the linear-time satisfaction
of the property. However, such a behavior is highly unfair, and such extreme executions
are normally ignored by using an explicit fairness assumption restricting the allowed
executions of the system. In our example assuming strong fairness [6] would do the
job. For linear-time satisfaction it is therefore necessary to add such an explicit fairness
condition.
result
lock
free
free
reject request
lock
request
lock
reject
free
yes
no
s
0
s
1
s
2
s
3
s
4
s
5
s
6
(a) Server
p
0
p
1
Σ
Σ
result
(b) Property
Fig. 1: An abstract server model and a property automaton.
Fig. 1. An abstract server model and a property automaton.
Applying IFLTV frees one from the need of finding an explicit fairness constraint
on the system model by having the fairness assumption inherently in the verification
relation’s definition. Therefore, not having to deal with fairness explicitly, can make
IFLTV quite useful in practice.
50

3 Preliminaries
We assume the reader is familiar with the most common notions of formal languages
and automata theory [8, 11]. For a finite set of system events Σ, let Σ
∗
be the set of all
finite strings over Σ, let Σ
ω
be the set of all infinite strings, and let Σ
∞
= Σ
∗
∪ Σ
ω
.
A language is a set L ⊆ Σ
∞
.
Let L be a language. Then the set of all finite prefixes of L is pre(L) = {w ∈
Σ
∗
|∃x ∈ Σ
∞
: wx ∈ L}. The continuation of w ∈ pre(L) in language L is
cont(w, L) = {x ∈ Σ
∞
|wx ∈ L}, and the set of all events en(w, L) which are
enabled in L after event sequence w occured is en(w, L) = pre(cont(w, L)) ∩ Σ.
Let A = (Q, Σ, δ, q
0
, F ) be a finite automaton, where Q is a finite set of states,
Σ is a finite set of symbols, q
0
∈ Q is the initial state, F ⊆ Q is a set of final states,
and δ : Q × Σ → 2
Q
is a transition relation. If δ(q, a) 3 p then we call (q, a, p) a
transition. For the rest of this paper, we assume the transition relation to be extended to
δ : 2
Q
× Σ
∗
→ 2
Q
in the usual way.
Let w = α
1
α
2
. . . ∈ Σ
ω
be an infinite string. A run of automaton A on w is a
sequence ρ(w) = r
0
r
1
. . ., such that r
i+1
∈ δ(r
i
, α
i+1
) for i ≥ 0. A run is called
successful if r
0
= q
0
and ω(ρ(w)) ∩ F 6= ∅ where ω(ρ(w)) is the set of all states
that occur infinitely often in ρ(w). Automaton A B
¨
uchi-accepts w if there is a suc-
cessful run of A on w. The infinite-string language accepted by B
¨
uchi automaton A is
L(A ) = {w ∈ Σ
ω
|A B
¨
uchi-accepts w}[3].
A state q ∈ Q of the automaton A is said to be reachable if there exists a path
from q
0
to q in A . A state q ∈ Q of A is said to be co-reachable if there exists a run
ρ(w) = q
1
q
2
. . . of A on some infinite string w such that q
1
= q and ω(ρ(w))∩F 6= ∅.
The behavior of a system and the properties are sets of infinitely long event se-
quences over Σ. We consider here behaviors and properties which can be represented by
B
¨
uchi automata. A behavior B satisfies the linear-time property P (written: ‘B |= P ’)
if and only if B ⊆ P . The satisfaction relation defined in this way is called linear-time
satisfaction relation. It follows that B ∩P = B is an equivalent definition of linear-time
satisfaction, since B can only be a subset of P if B = B ∩ P .
Throughout this paper, let P be a property and P = (Q
P
, Σ, δ
P
, q
P
, F
P
) be a B
¨
uchi
automaton such that L(P) = P , and let B be a behavior and B = (Q
B
, Σ, δ
B
, q
B
, F
B
)
be a B
¨
uchi automaton such that L(B) = B. An additional requirement for automaton
B is that all its states are accepting states, in other words F
B
= Q
B
,
1
and it can
therefore be assumed to be deterministic.
4 The IFLTV Relation and its Na
¨
ıve Checking Procedure
Instead of demanding B = B ∩ P as in the linear-time satisfaction relation, the defi-
nition of the IFLTV relation is obtained by relaxing the definition, requiring only that
finite prefixes of B have to equal the finite prefixes of B ∩ P . Thus, we define IFLTV
as
B satifies P inherently fairly ⇔ pre(B) = pre(B ∩ P ). (1)
1
The behavior is the Eilenberg-limit of a prefix-closed regular language, which immediately
implies that the corresponding B
¨
uchi automaton contains only accepting states.
51

Because pre(B ∩ P ) ⊆ pre(B) always holds (since B ∩ P ⊆ B), we can refine the
above definition to
B satifies P inherently fairly ⇔ pre(B) ⊆ pre(B ∩ P ). (2)
Informally, this definition states that a behavior satisfies a property inherently fairly, if
and only if all finite behaviors can be continued to an infinite behavior satisfying the
property. This observation, written more formally, gives us another way of representing
the IFLTV relation:
B satifies P inherently fairly ⇔ ∀v ∈ pre(B) : ∃x ∈ cont(v, B) : vx ∈ P. (3)
Formal proofs of the equivalence of the above-mentioned definitions can be found
in [9]. If B satisfies P inherently fairly, we write ‘B  P ’.
The second condition of checking whether or not pre(B) ⊆ pre(B ∩ P ) is equiv-
alent to checking whether or not pre(B) ∩ Σ
∗
\ pre(B ∩ P ) = ∅. Therefore we can
check the IFLTV relation na
¨
ıvely by (note that the following automata are interpreted
as B
¨
uchi or finite-string automata as appropriate):
1. Computing the product of B and P and reducing it if necessary (yielding B ∩ P ).
2. Changing all states in the resulting automaton to be final states (yielding pre(B ∩
P ))
3. Determinizing this automaton, making it complete, and interchanging final and
non-final states (yielding the complement automaton Σ
∗
\ pre(B ∩ P )).
4. Computing the product of the resulting automaton and B (yielding pre(B) ∩ (Σ
∗
\
pre(B ∩ P ))).
5. Checking whether or not the resulting automaton is empty (yielding the test pre(B)∩
(Σ
∗
\ pre(B ∩ P )) = ∅).
5 Checking Whether Linear-Time Properties are Satisfied
Inherently Fairly
With the help of some auxiliary lemmas, we will prove that the IFLTV relation can be
represented by the following conditions on a behavior B and a property P (the result is
stated in Corollary 2):
1. ∀v ∈ pre(B) : en(v, B) ∩ en(v, P ) = en(v, B) and
2. ∀v ∈ (pre(B) ∩ pre(P )) : cont(v, B ∩ P ) 6= ∅.
So checking IFLTV can be reduced to checking enabled conditions of individual
events in the behavior and the property (first condition), and checking the possible con-
tinuation of finite behaviors in the correct sub-behavior B ∩ P of behavior B (second
condition).
We first prove that IFLTV implies the following subset condition.
Lemma 1. B  P ⇒ pre(B) ⊆ pre(P ).
52

Proof. Let v ∈ pre(B). Then, by definition of “”, there is a w ∈ cont(v, B) such that
vw ∈ P . Hence v ∈ pre(P ). ut
We prove now that the subset condition is equivalent to the enabling condition we
want to show for the IFLTV relation.
Lemma 2. pre(B) ⊆ pre(P ) ⇔ ∀v ∈ pre(B) : en(v, B) ∩ en(v, P ) = en(v, B).
Proof. “⇒”: Let v ∈ pre(B) and let a ∈ en(v, B). Then va ∈ pre(B) and hence, by
Lemma 1, va ∈ pre(P ), implying a ∈ en(v, P ). Thus en(v, B) ⊆ en(v, P ), implying
en(v, B) ∩ en(v, P ) = en(v, B).
“⇐”: Let v ∈ pre(B) and let a ∈ en(v, B). Because en(v, B) ∩ en(v, P ) =
en(v, B), we get a ∈ en(v, P ). Therefore va ∈ pre(P ) and consequently v ∈ pre(P ).
Hence pre(B) ⊆ pre(P ). ut
Lemmas 1 and 2 together result in the following corollary:
Corollary 1. B  P ⇒ ∀v ∈ pre(B) : en(v, B) ∩ en(v, P ) = en(v, B).
To complete the prove in one direction, it remains to show that the second condition is
a consequence of the IFLTV relation, too.
Lemma 3. B  P ⇒ ∀v ∈ (pre(B) ∩ pre(P )) : cont(v, B ∩ P ) 6= ∅.
Proof. Let v ∈ (pre(B) ∩ pre(P )). Then in particular v ∈ pre(B). Then, by definition
of “”, there exist w ∈ cont(v, B) such that vw ∈ P . Hence vw ∈ B ∩ P , or equiva-
lently: w ∈ cont(v, B ∩ P ). Therefore cont(v, B ∩ P ) is not empty. ut
Having shown that the two conditions stated at the beginning of this section are a
consequence of the IFLTV relation, it remains to show that the two conditions together
also imply the IFLTV relation.
Lemma 4. Conditions
1. ∀v ∈ pre(B) : en(v, B) ∩ en(v, P ) = en(v, B) and
2. ∀v ∈ (pre(B) ∩ pre(P )) : cont(v, B ∩ P ) 6= ∅.
imply B  P.
Proof. Rewriting ∀v ∈ (pre(B) ∩ pre(P )) : cont(v, B ∩ P ) 6= ∅ yields
∀v ∈ (pre(B) ∩ pre(P )) : ∃w ∈ cont(v, B) : vw ∈ P. (4)
From ∀v ∈ pre(B) : en(v, B) ∩ en(v, P ) = en(v, B), taking into account Lemma 2,
we get pre(B) ⊆ pre(P ), implying pre(B) ∩ pre(P ) = pre(B). Then, substituting
pre(B) for pre(B) ∩ pre(P ) in Equation (4) yields ∀v ∈ pre(B) : ∃w ∈ cont(v, B) :
vw ∈ P , which is just the definition of B  P . ut
Summarizing the previous results, we establish a main result of this paper, which
we will use to construct a non-na
¨
ıve checking procedure for the IFLTV relation.
Corollary 2. B  P if and only if
1. ∀v ∈ pre(B) : en(v, B) ∩ en(v, P ) = en(v, B)
2. ∀v ∈ (pre(B) ∩ pre(P )) : cont(v, B ∩ P ) 6= ∅.
Proof. This corollary follows immediately from Corollary 1 and Lemmas 3 and 4. ut
53

6 The Non-Na
¨
ıve IFLTV Procedure
Both the behavior and the property are specified by automata. Since it is neccessary
to decide a subset condition on the intersection of these languages, we consider an
automaton A
B∩P
which accepts B∩P in order to check the IFLTV relation. So initially,
we construct the automaton A
B∩P
and throughout this construction, we check whether
for all prefixes of the behavior the enabled actions in the behavior are enabled actions in
the property as well, i.e., we check for a potential violation of the first condition given
in Corollary 2. If this condition is violated, the construction immediately aborts with
the result pre(B ) 6⊆ pre(B ∩ P ), i.e. B does not satisfy P inherently fairly. Otherwise
the construction succeeds and we obtain the automaton A
B∩P
. During the reduction of
A
B∩P
, we verify the second condition of Corollary 2.
For the purpose of checking the conditions of Corollary 2 we compute in parallel,
during the construction of A
B∩P
, sets of states of the property automaton. These sub-
sets correspond to the states of a ‘determinized’ version of P . They indicate whether
or not Corollary 2 is violated.
Let B = (Q
B
, Σ, δ
B
, q
0
, Q
B
) be the deterministic behavior automaton (recall that
behavior automata are always deterministic) and P = (Q
P
, Σ, δ
P
, p
0
, F
P
) be the
property automaton (potentially nondeterministic). Then
A
B∩P
= (Q
B
× Q
P
, Σ, δ, (q
0
, p
0
), Q
B
× F
P
),
where δ is defined by:
δ((u, r), a) 3 (v, s) ⇔
δ
B
(u, a) = v and δ
P
(r, a) 3 s, ∀u, v ∈ Q
B
, r, s ∈ Q
P
, a ∈ Σ.
We construct A
B∩P
stepwise starting with the initial state (q
0
, p
0
) and proceed as fol-
lows: Let (q, r) be a state of A
B∩P
not yet considered (at the beginning, there is just
the state (q
0
, p
0
)). Now, for every transition (q, a, p) of B and every matching transition
(r, a, s) of P we add the transition ((q, r), a, (p, s)) to A
B∩P
. If (p, s) is not yet a state
of A
B∩P
, we add it as well. If there exists no transition in (q, r) matching (q, a, p) and
furthermore, there is no alternative state (q, r
0
) in A
B∩P
with a matching transition,
then we abort, because in that case there exists a v ∈ pre(B ) such that v 6∈ pre(B ∩ P ),
to wit B 6 P . Here, an alternative state (q, r
0
) is a state that can be reached by the
same v ∈ Σ
∗
which passes A
B∩P
into (q, r). Due to the determinism of the behavior
automaton, the first component of each state that represents an alternative to state (q, r)
must still be q. Thus, we just have to collect the set of states of P that may occur in
the second entry, i.e., we maintain sets R
q
⊆ 2
Q
P
such that r
0
∈ R
q
if and only if there
exists a state (q, r
0
) in A
B∩P
which is an alternative to (q, r). Of course, the set which
corresponds to the state q
0
is initially {{p
0
}}
q
0
.
There are two possible termination scenarios: Either no more states and transitions
can be added, then the construction of the product automaton A
B∩P
is completed, or
we may have aborted the construction since we know already that B does not satisfy P
inherently fairly.
To check the second condition of Corollary 2, we remove from A
B∩P
all states
that are not co-reachable. The resulting automaton is denoted by A
B∩P,red
. Note that
54

due to our construction, each state in A
B∩P
is reachable. Detection of states which are
not co-reachable can be performed by using a combination of standard algorithms that
determine the strongly connected components of the transition graph of A
B∩P
and stan-
dard algorithms that reduce finite automata (see, for instance, [1, 5]). Now assume the
algorithm has determined the set of useless
2
states and has removed each of its elements
from A
B∩P
. Thus, after the reduction process, each state of A
B∩P,red
is reachable by
a v ∈ Σ
∗
such that cont(v, B ∩ P ) 6= ∅.
The last step of our IFLTV algorithm consists of updating the sets R
q
of sets of
states of P that are attached to each state of A
B∩P
. Of course, if a set R
q
contains
r
0
such that (q, r
0
) has been identified to be useless, then we have to remove r
0
from
each set in R
q
since (q, r
0
) no longer represents an alternative state. Now, if during
this deletion process a set R
q
of second-component-states becomes empty, we have
identified a v ∈ (pre(B )∩pre(P )) such that cont(v, B ∩ P ) = ∅, violating Corollary 2
and thus B 6 P . Otherwise, the reduction step terminates and all state sets R
q
contain
at least one state. Then we have B  P .
7 Correctness of the Construction
Given automata that accept the behavior B and the property P respectively, we ap-
ply the usual product construction to obtain the automaton A
B∩P
which accepts the
intersection B ∩ P . Note that the computation of the sets R
q
of alternative second com-
ponents of states in A
B∩P
does affect in no way the final product automaton A
B∩P
but
rather is supplementary. Hence L(A
B∩P
) = B ∩ P .
Mainly, we will prove that our construction implements accurately the two condi-
tions of Corollary 2 and for this reason verifies correctly whether or not B satisfies P
inherently fairly. So we verify first
Theorem 1. For all v ∈ pre(B ): en(v, B)∩en(v, P ) = en(v, B) ⇔ The construction
of A
B∩P
succeeds.
Proof. “⇒” To each v ∈ pre(B ) there is a state q ∈ Q
B
such that δ
B
(q
B
, v) = q. The
set en(v, B) contains all symbols a ∈ Σ such that δ
B
(q, a) 6= ∅. Furthermore, these
symbols are elements of en(v, P ) as well. It follows that in P, there is at least one
state r such that δ
P
(q
P
, v) 3 r and δ
P
(r, a) 6= ∅. But then, due to the definition, r is in
the set of alternative second-component-states R
q
and δ
P
(R
q
, a) 6= ∅. This shows the
existence of a matching transition. Since this holds for all v ∈ pre(B ), the construction
of A
B∩P
succeeds.
“⇐” For all v ∈ pre(B ) there is a state q ∈ Q
B
such that δ
B
(q
B
, v) = q. Moreover,
en(v, B) 6= ∅ and for all a ∈ en(v, B) there is a p ∈ Q
B
and δ
B
(q, a) = p. Since
the construction of A
B∩P
succeeded and was not aborted due to lack of a matching
transition, it follows that each transition of B has at least one corresponding transi-
tion in A
B∩P
. Consequently, there exist states (q, r) and (p, s) of A
B∩P
such that
δ((q
B
, q
P
), v) 3 (q, r) and δ((q, r), a) 3 (p, s). This implies that in P we have
δ
P
(q
P
, v) 3 r and δ
P
(r, a) 3 s. Hence, a ∈ en(v, P ) implying en(v, B) ∩ en(v, P ) =
en(v, B) for all v ∈ pre(B ). ut
2
We refer to a state as being useless, whenever this state is not co-reachable.
55

Theorem 2. For all v ∈ (pre(B ) ∩ pre(P )) : cont(v, B ∩ P ) 6= ∅ ⇔ No set R
q
,
q ∈ Q
B
, becomes empty after removing useless states.
Proof. “⇒” For all v ∈ (pre(B) ∩ pre(P )), we have δ((q
B
, q
P
), v) 6= ∅ due to the
construction of A
B∩P
. Since L(A
B∩P
) = B ∩ P and there is a w ∈ cont(v, B ∩ P ),
at least one element of δ((q
B
, q
P
), v) is co-reachable. Thus, there exists a successful
run ρ(vw) of A
B∩P
on vw. Obviously, none of the states of ρ(vw) will be removed by
the reduction process, or in other words, all corresponding sets of second-entry-states
contain at least one element after A
B∩P
has been reduced and the sets R
q
have been
updated. According to the construction of A
B∩P
, each of its states can be reached by a
v ∈ (pre(B)∩pre(P )), and thus occurs in a successful run. This means that each of the
sets R
q
of second-component-states, which are attached to a state in that run, contains
at least one element even after the reduction- and update-process.
“⇐” It follows that for each v ∈ (pre(B )∩pre(P )) that leads A
B∩P
to one of its states,
there is at least one state in the reduced automaton A
B∩P
that is reached by v. Since
each state of the reduced A
B∩P
is co-reachable and the reduced automaton A
B∩P
still
recognizes B ∩ P , it implies the existence of a w ∈ cont(v, B ∩ P ). Furthermore, due
to the construction of A
B∩P
, every v ∈ (pre(B) ∩ pre(P )) leads A
B∩P
to one of its
states. Thus, for all v ∈ (pre( B ) ∩ pre(P )) there is a w ∈ cont(v, B ∩ P ). ut
Corollary 3. The presented IFLTV procedure verifies correctly whether or not B sat-
isfies P inherently fairly.
Proof. Follows immediately from the theorems above and Corollary 2. ut
8 Complexity of the Procedure
It has been shown that deciding IFLTV is PSPACE-complete [9]. So the only complex-
ity criterion for evaluating our algorithm is whether or not it requires less computation
steps than the previously known algorithms, even though it remains inefficient in the
worst case. However, it can be seen that the presented procedure is more efficient than
the na
¨
ıve one, and, we think that it is worth being considered as an alternative to current
model-checking algorithms for verifying liveness properties under fairness constraints.
Our procedure for the IFLTV relation is divided into two major steps, construction
of the product automaton and reduction of this automaton. During the construction of
the product automaton, we compute the sets we need for the verification task. These sets
corresponds to the states of a determinized product automaton, so what we do is in fact
a determinization of the product automaton. The second step of reduction, is obtained
by computing the strongly connected components of the product automaton.
Compared to the na
¨
ıve algorithm for IFLTV, which needs to compute the product
automata twice, build the complement automaton, determinize once and do an empti-
ness check, the described procedure is more efficient, which only needs to compute one
product automaton, one determinization and one reduction of the automaton. Further,
our procedure has an integrated on-the-fly check, which means the procedure may stop
whenever a violation of one of the two criteria mentioned above has been detected.
56

9 Conclusions and Outlook
The presented construction avoids several steps of the na
¨
ıve procedure, and the verifica-
tion is done on-the-fly. Part of our immediate future work will be experimenting with an
implementation of our approach to tackle complex, industrial-sized case studies. In ad-
dition, the resulting procedure still seems to offer scope for improvement. For example,
the construction of the product states of the property automaton in parallel with the con-
struction of the behavior-and-property product automaton could be improved by giving
up the requirement of being able to detect a violation of Condition 1 of Corollary 2 on
the fly, i.e. immediately during the construction of the product automaton: Checking
the second condition first, and only then the first condition would make it possible to
reduce the automaton before determinization, but on the cost of losing the on-the-fly
effect. Exploring these potential improvements will also be part of our future work.
We believe the IFLTV is tailored to model checking liveness properties under fair-
ness constraints. And as model-checkers do not or only partly offer fairness implemen-
tation, we will try to integrate the given procedure into an existing model-checker. Such
an implementation would allow us to compare our approach with existing algorithms.
References
1. A. V. Aho, J. E. Hopcroft, and J. D. Ullman. The Design and Analysis of Computer Algo-
rithms. Addison-Wesley, Reading, Mass., first edition, 1974.
2. B. Alpern and F. B. Schneider. Defining liveness. Information Processing Letters, 21(4):181–
185, October 1985.
3. J. R. B
¨
uchi. On a decision method in restricted second order arithmetic. In E. Nagel et al.,
editors, Proceedings of the International Congress on Logic, Methodology and Philosophy
of Science 1960, pages 1–11. Stanford University Press, 1962.
4. E. M. Clarke, O. Grumberg, and D. A. Peled. Model Checking. The MIT Press, 1999.
5. S. Eilenberg. Automata, Languages and Machines, volume A. Academic Press, New York,
1974.
6. N. Francez. Fairness. Springer Verlag, New York, first edition, 1986.
7. R. Gerth, D. Peled, M. Y. Vardi, and P. Wolper. Simple on-the-fly automatic verification of
linear temporal logic. In P. Dembinski and M. Sredniawa, editors, Protocol Specification,
Testing, and Verification XV ’95, pages 3–18. Chapman & Hall, 1996.
8. J. E. Hopcroft, R. Motwani, and J. D. Ullman. Introduction to Automata Theory, Languages
and Computation. Addison Wesley Longman, 2001.
9. U. Nitsche and P. Wolper. Relative liveness and behavior abstraction (extended abstract).
In Proceedings of the 16th ACM Symposium on Principles of Distributed Computing
(PODC’97), pages 45–52, Santa Barbara, CA, 1997.
10. S. St James and U. Ultes-Nitsche. Computing property-preserving behaviour abstractions
from trace reductions. In Proceedings of the 20th Annual ACM Symposium on Principles of
Distributed Computing (PODC 2001), pages 238–245. ACM Press, August 2001.
11. W. Thomas. Automata on infinite objects. In J. van Leeuwen, editor, Formal Models and Se-
mantics, volume B of Handbook of Theoretical Computer Science, pages 133–191. Elsevier,
1990.
12. U. Ultes-Nitsche and S. St James. Improved verification of linear-time properties within fair-
ness — weakly continuation-closed behaviour abstractions computed from trace reductions.
Software Testing, Verification and Reliability (STVR), 13(4):241–255, 2003.
57

13. M. Y. Vardi and P. Wolper. An automata-theoretic approach to automatic program verifica-
tion. In Proceedings of the 1st Symposium on Logic in Computer Science, Cambridge, June
1986.
14. M. Y. Vardi and P. Wolper. Reasoning about infinite computations. Information and Compu-
tation, 115(1):1–37, November 1994.
58