
MODELING PROCESSES FROM TIMED OBSERVATIONS
Marc Le Goc
1
, Emilie Masse
1,2
1
LSIS, Laboratory for Systems and Information Sciences, UMR CNRS 6168
Aix-Marseille University, Marseilles, France
Corinne Curt
2
2
Cemagref, Unit´e Ouvrages Hydrauliques et Hydrologie, Aix en Provence, France
Keywords:
Multi modeling, diagnosis reasoning, dynamic system.
Abstract:
This paper presents a modelling approach of dynamic process for diagnosis that is compatible with the Stochas-
tic Approach framework for discovering temporal knowledge from the timed observations contained in a
database. The motivation is to define a multi-model formalism that is able to represent both the knowledge
of these two sources. The aim is to model the process at the same level of abstraction that an expert uses to
diagnose the process. The underlying idea is that at this level of abstraction, the model is simple enough to
allow an efficient diagnosis. The proposed formalism represents the knowledge in four models: a structural
model defining the components and the connection relations of the process, a behavioural model defining the
states and the transitions states of the process, a functional model containing the logical relations between the
values of the process’s variables, which are defined in the perception model. The models are linked with the
process’s variables. This point facilitates the analysis of the consistency of the four models and is the basis of
the corresponding knowledge modelling methodology. The formalism and the methodology is illustrated with
the model of a hydraulic dam of Cublize (France).
1 INTRODUCTION
The design of knowledge based systems to supervise,
diagnose and control industrial processes pose the dif-
ficult problem of the acquisition and the representa-
tion of temporal knowledge which is the core of the
solving problem method of dynamic system diagnosis
(Basseville and Cordier, 1996).
The aim of the MultiModel Based Diagnosis
(MMBD) is to solve this problem. One of the major
difficulties is the definition of the right level of ab-
straction at which the models have to be constructed
to have an efficient diagnosis. This investigation be-
ing still an open problem, most of the proposed mod-
eling approaches use the abstraction level of the avail-
able models, typically the design model(s). But the
abstraction level required to the design of a process re-
quires the definition of a lot of components. Using the
design model(s) leads then to diagnosis models con-
taining a large number of components. Such models
entails strong computational difficulties for the usual
diagnosis algorithms.
Our works consist then in developing a modeling
method, called TOM4D (Timed Observations Mod-
eling for Diagnosis) with the aim of using the same
level of abstraction that the Experts use to diagnose a
process: defined at this level of abstraction, the mod-
els lead up to a minimal set of components allowing
an efficient and sure diagnosis reasoning. This notion
of minimality is intuitive: only the components that
are concerned with a diagnosis have to be identified in
the models. Consequently, when using such models,
the computational difficulties of the usual diagnosis
algorithms will decrease. The TOM4D methodology
is based on the idea that the Experts use implicit mod-
els to formulate their knowledge about the process
and the way to diagnose about it. The methodology
aims then to explicit these models when combining
a CommonKads-like conceptual approach (Schreiber
et al., 2000) with a multimodeling approach (Chittaro
et al., 1993) and the Stochastic Approach framework
for discovering temporal knowledge from timed ob-
servations (Le Goc et al., 2005), (Le Goc, 2006). The
modeling methodology is directed by the timed obser-
vations provided either with a set of scenarios describ-
ing a concrete deterioration of a process or with the a
priori knowledge about the main events that plays a
role in the different diagnosis. The next section of
249
Le Goc M., Masse E. and Curt C. (2008).
MODELING PROCESSES FROM TIMED OBSERVATIONS.
In Proceedings of the Third International Conference on Software and Data Technologies - PL/DPS/KE, pages 249-256
DOI: 10.5220/0001884502490256
Copyright
c
SciTePress

the paper (Section 2) provides a brief overview of the
main modeling approaches. Section 3 presents the
formalisms of the four models of the TOM4D mod-
eling methodology, and section 4 describes the corre-
sponding modeling process through a real world ap-
plication to the Cublize dam (France). Finally, section
5 states our conclusions and proposes some perspec-
tives to our works.
2 MODELING APPROACHES
FOR DIAGNOSIS
The limitations and the problems of the heuristic ap-
proach (Clancey, 1987) have motivated the definition
of the Model Based Diagnosis (MBD) approach (Re-
iter, 1987). Reiter’s algorithm of diagnosis uses a
logical model of the system. This model represents
both the structure of the system (components and in-
terconnections) and the correct behaviors of the com-
ponents through a set of relations between input and
output values of the components. The MBD, either
in a component (De Kleer and Brown, 1984), in a
process (Forbus et al., 1984) or in a constraint (Lee
and Kuipers, 1988) based approach, applies the well
known “no function in structure” principle. This pro-
vides a clear and general framework for diagnosis.
Nevertheless, these approaches present two ma-
jor drawbacks. First, the number of potential di-
agnosis is exponential with the number of compo-
nents. This leads to several difficulties with real
world systems where the number of components is
large. Second, even when the system contains few
components, the consistency based theory of diagno-
sis provides no means to eliminate diagnosis which
are logically acceptable but physically meaningless
(Struss and Dressler, 1989). A lot of extensions have
then been proposed to avoid these difficulties (Dague,
2001): using different levels of aggregation (Davis,
1984) corresponding to different approximations, us-
ing ontologies that represent the variable values at
multiple resolutions level (Hayes, 1989), using differ-
ent behavioral models either qualitative or quantita-
tive models (Murthy, 1988), and using multiple types
of knowledge (Abu-Hanna et al., 1991). Neverthe-
less, there is not a general solution to these problems.
Moreover, none of these approaches really explains
how to export partial results obtained with a model
into other models during the problem solving task.
This has led researchers to give up the “no func-
tion in structure” principle with the aim of using some
teleological and functional knowledge. This provides
information for driving the diagnosis reasoning about
the structure and the behavior of the system. For ex-
ample, the compositional modeling of (Falkeihainer
and Forbus, 1988), (Falkeihainer and Forbus, 1991),
uses the ideas of the Qualitative Physics theory. An
explicit abstract representation of the process is then
given where a model is made of fragments from a
general-purpose domain theory. Similarly, the Func-
tion Behavior Structure approach (FBS) of (Franke,
1991) and the multimodeling approach of (Chittaro
et al., 1993) consider the reasoning task as a cooper-
ative activity between diverse models. Each model
represents a specific type of knowledge and uses a
specific representation formalism. Both approaches
separate on one hand the structural and the behavioral
knowledge about the physical system and on the other
hand the knowledge about the functions and the pur-
poses of the system. But only the multimodeling ap-
proach proposes a physical basis for the relations be-
tween the different models.
The multimodeling approach of (Chittaro et al.,
1993) separates the available knowledge about a dy-
namic system in three main categories: the funda-
mental, the interpretative and the empirical knowl-
edge. The fundamental knowledge is the basic knowl-
edge (structural and behavioral models) used to rea-
son about a system using the objective and neutral lan-
guage of natural sciences (Chittaro et al., 1993). The
interpretative knowledge is provided by a subjective
interpretation of the fundamental knowledge. This in-
terpretation is made in terms of functions (functional
model) and goals (teleological model) of the system
components assigned by the designer(s). The empir-
ical knowledge is an explicit statement of the proper-
ties of the system and may refer to the two other cate-
gories. These three sets of knowledge are based on an
ontology which defines the type of entities the system
is made with. The functional model links the behav-
ioral model and the teleological model. The role of
a function is to describe how the behavior of the in-
dividual components contributes to the achievement
of a goal assigned to the system. The links between
the models allow a good continuity for modeling and
reasoning.
The behavioral model is the key point of the mul-
timodeling approach, notably because the diagnosis
reasoning process is based on this model. Behavioral
models are build according to physical equations of
the system studied. This set of equations is difficult
to determine because there is an important number of
physical laws to respect. So the bond-graph concept
has been used to facilitate the determination of these
equations and the modeling of the behavior of compo-
nents and the generation of functional roles (Zouaoui
et al., 1997). These functional roles are identified
by the interpretation of the behavior of a system or
ICSOFT 2008 - International Conference on Software and Data Technologies
250

more precisely of its physical equations. The bond
graph approach (Rosenberg and Karnopp, 1983) ex-
presses system dynamics in terms of energy trans-
fer between constituent elements and more precisely
based on power echanges. This approach is based
on the tetrahedron of state which represents the rela-
tions between effort and power variables. It allows the
construction of dynamic system models. Neverthe-
less, the behavioral model and the functional model
are closed to the set of components (Thetiot, 1999)
because in most cases the “a priori” knowledge is
mainly provided by the design model of the system.
Thereby, the diagnosis process is still concerned with
computational problems. There is then a crucial need
to define the right level of abstraction for modeling
with a level of aggregation that allows an efficient di-
agnosis process.
So, in this paper, we propose to use the same level
of abstraction the Experts use to diagnose a dynamic
system. This level of abstraction corresponds to a
level of aggregation that minimizes the set of compo-
nents and thereby improves the computational prob-
lem. This corresponds to associate the abstraction
level with the diagnostic task and not with the design
task.
3 TOM4D MODELING METHOD
TOM4D (”Timed Observations Multimodeling for
Diagnosis”) is a timed observations centered model-
ing method for dynamic systems or processes. The
aim of this method is to produce a model from a set
of sequences of timed observations and the a pri-
ori expert’s knowledge, the so produced model be-
ing used to diagnose a dynamic process. The main
constraints to define the TOM4D method is that the
modeling formalisms must be compatible with (i) the
Stochastic Approach Framework for discovering tem-
poral knowledge from timed data of (Le Goc, 2006),
(Le Goc and B´enayadi, 2008), (ii) the conceptual mul-
timodeling framework of (Zanni et al., 2005) and (iii)
the diagnosis algorithm of (Reiter, 1987).
3.1 The Stochastic Approach
Framework
The Stochastic Approach Framework of (Le Goc,
2006), (Le Goc and B´enayadi, 2008) for discover-
ing temporal knowledge from timed data provides a
general framework for modeling dynamic processes.
This framework considers that the timed messages
of a series are written in a database by a program,
called a monitoring cognitive agent MCA, that mon-
itors, diagnoses or controls a production process Pr.
A timed message is represented with an occurrence
o(t
k
) ≡ (δ
i
, k) of a discrete event class C
i
= {(x
i
, δ
i
)}
that is an arbitrary set of discrete event e
i
≡ (x
i
, δ
i
),
where δ
i
is one of the discrete value of the variable
x
i
. A discrete event class is often a singleton because
in that case, two discrete event classes C
i
= {(x
i
, δ
i
)}
and C
j
= {(x
j
, δ
j
)} are only linked with the variables
x
i
and x
j
when the constants δ
i
and δ
j
are independent
(Le Goc, 2006). This condition is only concerned
with the programs the MCA is made with. This means
that a relation between the occurrences of two classes
C
i
and C
j
subsumes a relation between the corre-
sponding two functions x
i
(t) and x
j
(t). A sequence of
discrete event class occurrences is then considered as
the observable manifestation of a series of state transi-
tions in a timed stochastic automaton representing the
couple (Pr, MCA). The BJT4G algorithm represents
a set of sequences of discrete event class occurrences
with a Markov chain and apply an abductive reason-
ing on this representation to identify the set M =
{R
ij
(C
i
,C
j
, [τ
−
ij
, τ
+
ij
])} of the most probable timed se-
quential binary relations R
ij
(C
i
,C
j
, [τ
−
ij
, τ
+
ij
]) between
discrete event classes leading to a given class. A
timed sequential binary relation R
ij
(C
i
,C
j
, [τ
−
ij
, τ
+
ij
])
is an oriented relation between two discrete event
classes C
i
and C
j
that is timed constrained with the
interval [τ
−
ij
, τ
+
ij
]. [τ
−
i, j
, τ
+
i, j
] is the time interval for ob-
serving an occurrence of the C
j
class after an occur-
rence of the C
i
class. The set M of timed sequential
binary relation is an abstract chronicle model that is
graphically represented with the ELP language (Event
Language for Process) where the nodes are discrete
event classes and the links are timed sequential binary
relations.
3.2 TOM4D Model Formalisms
The conceptual multimodeling framework of (Zanni
et al., 2005) organizes the available knowledge about
a process according to three models: a Structural
Model describing the relations between the compo-
nents of the process, a Functional Model providing
the relations between the values of the process vari-
ables (i.e. a set of mathematical functions) and a Be-
havioral Model defining the states of the process and
the discrete events firing the state transitions.
The TOM4D method extends this framework to
add a complementary model, called the Perception
Model (PM) of the process. This model specifies
the process P(t) = R(x
1
(t), . . . , x
i
(t), . . . , x
n
(t)) as a
relation between n variables x
i
of a set X = {x
i
}
and a set {Q
i
(x
i
, δ
i
)} of constraints about the val-
MODELING PROCESSES FROM TIMED OBSERVATIONS
251

ues of the process variables. The Structural, Func-
tional and Behavioral models must be deduced from
Given PM. Consequently,with the TOM4D method, a
model M(P(t)) of a process is a quadrupletM(P(t)) =
hPM, SM(P(t)), FM(P(t)), BM(P(t))i.
The Perception Model PM = hΨ, X, R
q
i defines
the process P(t) and its operating modes:
• Ψ = {ψ
i
} is a set of constants ψ
i
typically corre-
sponding to thresholds;
• X(t) = {x
i
(t)} ⊆ V(t) is a sub set of all the mea-
sured variables V(t) of the process;
• R
q
= {
∏
(Q
i
(x
i
(t), ψ
i
)} is a set of binary predicate
conjunctions Q(x
i
, ψ
i
) linking a variable x
i
∈ X
and a constant ψ
i
∈ Ψ. These predicates formu-
late some constraints about the values of the pro-
cess variables x
i
. R
p
is partitioned in three parts
C
g
∪C
n
∪C
a
(i.e. C
g
∩C
n
∩C
a
= {φ}):
– C
g
contains the sub set of R
p
describing the pro-
cess operating goals;
– C
n
contains the sub set of R
p
describing the nor-
mal operating modes of the process;
– C
a
contains the sub set of R
p
describing the ab-
normal operating modes of the process;
The Structural Model SM(P(t)) =
hCOMPS, R
i
, R
x
i of a process P(t) describes re-
lations between components of the system and the
relations between the components and the variable
X(t) of P(t):
• COMPS = {c
i
} is a set of components
c
i
≡ {{e
i
(c
i
)}, {s
i
(c
i
)}} where {e
i
(c
i
)} (resp.
{s
i
(c
i
)}) is the set of input (reps. output) ports of
the component c
i
;
• R
i
= {= (s
i
(c
i
), e
j
(c
j
))} is a set of assignment of
the binary predicate ’Equal’ linking an output of
a component c
i
with an input of the component c
j
(i.e. the interconnection relations);
• R
x
= {= (x
i
(t), s
i
(c
i
))} is a set of assignment of
the binary predicate ’Equal’ linking each variable
x
i
(t) ∈ X(t) with an output s
i
of a component c
i
∈
COMPS.
The Functional Model FM(P(t)) = h∆, F, R
f
i of a
process P(t) describes the relations between the val-
ues δ
i
of the variables x
i
∈ X with mathematical func-
tions:
• ∆ = {
S
∆
x
i
}
S
{φ} is the union of the sets ∆
x
i
=
{δ
i
} of constants associated with each variable
x
i
of X. The sets ∆
x
i
= {δ
i
} is deduced from
the set Ψ = {ψ
i
} of the Perception Model PM
when applying the ”Spatial Discretization Prin-
ciple” of the Stochastic Approach Framework (Le
Goc et al., 2005). The constant φ is added to as-
sign an unknown value to a variable.
• F = { f
i
(x
1
(t), x
2
(t), ..., x
m
(t))} is a set of func-
tion f
i
(x
1
(t), x
2
(t), ..., x
m
(t)) linking each value of
the variables x
1
(t), x
2
(t), ..., x
m
(t) with the out-
put value of the function f
i
(x
1
(t), x
2
(t), ..., x
m
(t)).
Typically, these functions are defined with tables
of values.
• R
f
= {= (x
i
(t), f
i
(x
1
(t), x
2
(t), ..., x
m
(t)))} is a set
of assignments of the binary predicate ”Equal”
linking the value of a variable x
i
with the output
values of a function f
i
(x
1
(t), x
2
(t), ..., x
m
(t))).
The Functional Model FM(P(t)) specifies the rela-
tions between the variables x
i
of the process P(t) but
any mention about the normal and the abnormal val-
ues is contained in FM(P(t)). These properties are
deduced from the Behavioral Model of P(t).
The Behavioral Model BM(P(t)) = hS,C, R
c
i of a
process P(t) describes its operating modes (accord-
ing to (Chittaro et al., 1993)) with a set of states and
discrete event classes firing the state transitions:
• S = {s
i
} is a set of distinguishable states. Each
state s
i
is identified with a unique value X
i
≡
{(x
i
= δ
i
)} of X(t) so that:
– X(t) = X
i
⇔ ∀x
i
(t) ∈ X(t), ∃δ
i
∈ ∆, x
i
(t) = δ
i
.
– ∀s
i
, s
j
∈ S, s
i
= s
j
⇔ X
i
= X
j
.
• C = {C
i
} ∪C
φ
is a set of classes C
i
= {e
i
} of dis-
crete event e
i
= (x
i
, δ
i
). C
φ
= {e
φ
} is a techni-
cal class containing the event e
φ
= (φ, φ) which
matches with the observation of a date. In this
modeling context, each class C
i
= { e
i
} is a sin-
gleton (i.e. C
i
= {e
i
} = {(x
i
, δ
i
)}).
• R
c
= { = (s
i
, γ
i
(C
i
, s
j
)} is a set of assignment of
the binary predicate ”Equal” linking a state s
i
to
a state s
j
conditioned with the observation of an
occurrence of the class C
i
.
Given a sequence ω = {o(k)} of discrete event
class occurrences o(k) ≡ (δ
i
,t
k
), a transition from the
state s
i
to the state s
j
is fired when:
• there is an occurrence o(k) ≡ (δ
i
,t
k
) of the class
C
i
= {e
i
}, e
i
= (x
i
, δ
i
), in ω;
• the currentstate s(t) of the finite state machine im-
plementing BM(P(t)) is in the state s
i
(i.e. s(t) =
s
i
);
• there exist an assignment = (s
i
, γ
i
(C
i
, s
j
)) in R
c
.
In that case, the new value of the current state s(t)
is provided with the σ function defined on S × ω ×
R
c
→ S of a finite state machine such as s(t
k
) =
σ(s(t),o(k), R
c
):
• ∀t
k
≥ t, ∀o(k) ∈ ω, ∀s
i
∈ S, ∀ = (s
i
, γ
i
(C
i
, s
j
)) ∈ R
c
s(t) = s
i
∧ o(k) ≡ (δ
i
,t
k
) ∧C
i
= {(x
i
, δ
i
)},
⇒ σ(s(t), o(k), R
c
) = γ
i
(C
i
, s
j
)
ICSOFT 2008 - International Conference on Software and Data Technologies
252

According to the set R
q
of constraints in the Per-
ception Model PM of the process P(t), the set S of
states BM(P(t)) can be partitioned in three categories
S
g
∪ S
n
∪ S
a
(i.e. S
g
∩ S
n
∩ S
a
= φ):
• A set S
g
containing the states satisfying the pro-
cess operating goals of P(t):
∀s
i
∈ S
g
, ∃
∏
(Q(x
i
, δ
i
)) ∈ C
g
,
s(t) = s
i
⇒ X(t) = X
i
X(t) = X
i
⇒
∏
(Q(x
i
, δ
i
))
• A set S
n
⊆ S containing the states corresponding
to the normal operating modes of P(t):
∀s
i
∈ S
n
, ∃
∏
(Q(x
i
, δ
i
)) ∈ C
n
,
s(t) = s
i
⇒ X(t) = X
i
X(t) = X
i
⇒
∏
(Q(x
i
, δ
i
))
• A set S
a
⊆ S containing the states corresponding
to the abnormal operating modes of P(t):
∀s
i
∈ S
a
, ∃
∏
(Q(x
i
, δ
i
)) ∈ C
a
,
s(t) = s
i
⇒ X(t) = X
i
X(t) = X
i
⇒
∏
(Q(x
i
, δ
i
))
Consequently, the S
a
set of states defines the ab-
normal values X(t) = X
i
of the variables x
i
of P(t). So
the qualification ”normal value” or ”abnormal value”
depends on the states:
• ∀t ∈ ℜ, ∀s
i
∈ S
a
,
s(t) = s
i
⇒ X(t) = X
i
∧ AB(s(t))
• ∀t ∈ ℜ, ∀s
i
∈ S
g
∪ S
n
,
s(t) = s
i
⇒ X(t) = X
i
∧ ¬AB(s(t))
The Perception Model PM = hΨ, X, R
q
i, the
Structural Model SM(P(t)) = hCOMPS, R
x
, R
s
i, the
Functional Model FM(P(t)) = h∆, F, R
f
i and the Be-
havioral Model BM(P(t)) = hS,C, R
c
i degining a pro-
cess P(t) are linked together with the variable set
X = {x
i
}:
• each component c
i
∈ COMPS is linked with at
least one variable x
i
∈ X through a relation
= (x
i
(t), s
i
(c
i
)) in R
x
;
• each function f
i
(x
1
(t), x
2
(t), ..., x
m
(t)) ∈ F is
linked with at least one variable x
i
∈ X through a
relation = (x
i
(t), f
i
(x
1
(t), x
2
(t), ..., x
m
(t))) in R
f
;
• each state transition = (s
i
, γ
i
(C
i
, s
j
) ∈ R
c
is linked
with at least one variable x
i
∈ X through a discrete
event class C
i
= {(x
i
, δ
i
)} in C.
4 TOM4D MODELING PROCESS
The TOM4D method is made with three steps (cf.
Figure 1) aiming at producing a model M(P(t)) =
hPM, SM(P(t)), FM(P(t)), BM(P(t))i from the avail-
able knowledge and data. The Knowledge Inter-
pretation step uses a CommonKADS-like template
1. Knowledge interpretation Template CommonKADS
Knowledge gives by
experts
Generic
Model
Knowledge
Source
3. Generic modeling T.O.S.
Perception
Model
2. Process definition
Scenario
Model
Figure 1: TOM4D Modeling Process.
(Schreiber et al., 2000) to interpret and organize the
available knowledge about a process (i.e. the knowl-
edge conceptual model of Sachem (Le Goc, 2004) in
the example of this paper). This knowledge is pro-
vided by a knowledge source (an expert, a set of doc-
uments, etc) and at least one scenario ω = {x
j
(t
0
) =
δ
j
, . . . , x
i
(t
k
) = δ
i
, . . .} describing a typical evolution
of the process with a series of timed measures x
i
(t
k
) =
δ
i
. This first step produces then the scenario model
M(ω) = hSM(ω), FM(ω), BM(ω)i of the process that
is coherent with the scenario ω = {o
i
(t
k
) ≡ (δ
i
, k)}
when formulated with a series of occurrences o
i
(t
k
)
of discrete event classes C
i
= {(x
i
, δ
i
)}. The Process
Definition step aims at defining the Perception Model
(PM) of the process from the available knowledge
and the scenario model M(ω). Finally, the Generic
Modeling step uses the tetrahedron of states (TOS,
(Rosenberg and Karnopp, 1983)) to provide a ”physi-
cal” dimension to each variable x
i
of the process P(t)
and an interpretation of the relations linking the vari-
ables between them. The analysis of the properties of
the perception model PM with this interpretation pro-
duces some knowledge about the process that is dis-
tributed in the different parts of the model M(P(t)).
This model is called the ”Generic Model” of the pro-
cess because it is independent of the concrete instru-
mentation. This section explains the steps 2 and 3 of
the TOM4D modeling process trough its application
with a real world process, the Cublize dam (France)
that has been diagnosed wy the Expert’s of the Cema-
gref, the French governmental organization that as-
sumes the security of French hydraulic civil engineer-
ing structures. The step 1, the Knowledge Interpreta-
tion step), produces the scenario model M(ω) that is
presented in (Masse and Le Goc, 2007).
This scenario model leads to define the process
P(t) as a relation P(t) = R(V(t), Qs(t), Qf(t)) be-
tween three variables: a volume V(t) and two out-
flows, a ”normal” outflow Qs(t) and a water leak out-
MODELING PROCESSES FROM TIMED OBSERVATIONS
253

flow Qf(t). The following constraints have been de-
duced from M(ω):
• The goal of the process operations is to avoid any
water leak outflow:
– ∀t, Qf(t) = Qfmin
• Two normal process operations have been iden-
tified, one before the first dam’s filling and one
after:
– ∃t
i
, ∀t < t
i
,V(t) = Vmin ∧ Qs(t) = Qsmin ∧
Qf(t) = Qfmin
– ∃t
i
, ∀t ≥ t
i
,Vmax > V(t) > Vmin ∧ Qsmax >
Qs(t) > Qsmin ∧ Qf(t) = Qfmin
• Three abnormal process operations have been
identified:
– ∃t
j
> t
i
, ∀t ≥ t
j
, Qs(t) ≤ Qsmin
– ∃t
j
> t
i
, ∀t ≥ t
j
, Qs(t) ≥ Qsmax
– ∃t > t
i
, Qf(t) > Qfmin
Consequently, the set X of the process variable is
then:
• X(t) = {V(t),Qs(t), Qf(t)};
the set of threshold constants is:
• Ψ = {Vmax,Vmin, Qfmax, Qfmin, Qsmax, Qsmin};
and the set of constraints is
• R
q
= { (Qf(t) = Qfmin), (Vmax > V(t) >
Vmin) ∧ (Qsmax > Qs(t) > Qsmin) ∧ (Qf(t) =
Qfmin), (Qs(t) ≤ Qsmin), (Qs(t) ≥ Qsmax),
(Qf(t) > Qfmin)}.
This mean that the Perception Model PM = hΨ, X, R
q
i
is only concerned with a filled dam.
The hydraulic TOS of Figure 2 (b) provides a
physical dimension to the variables of X(t) leading to
define the structural model SM(P(t)) of P(t) as a pipe
(a glass, Figure 2a) with a constant capacity C that
contains a variable volume V(t) of water and that is
closed with a permeable stopper (a porous cork). The
resistivity to water of the stopper evolve as a not mea-
sured variable denoted R(t). The relation between the
volume V(t) and the outflow Qs(t) is made through
the pressure Pr(t) on the top of the stopper, which is
not measured. So the complete set of variable is:
• {V(t), Qs(t), Qf(t), Pr(t), R(t)},
but the generic process is instrumented with only
three abstract sensors measuring the outflow Qs(t)
through the stopper, the outflow over the pipe Q f(t)
and the volume V(t) of the column of water in the
pipe.
The Structural Model SM(P(t)) =
hCOMPS, R
i
, R
x
i of P(t) is then made with three
components:
Qs(t)
V(t)
Qf(t)
Qs(t)
V(t)V(t)
Qf(t)Qf(t)
V(t) Pr(t)
Qv(t)
V(t) = C.Pr(t)
Pr(t) = R(t).Qs(t)
Qv(t)=dV(t)/dt
Qs(t)
(a) (b)
Figure 2: (a) Structural Model and (b) TOS Relations.
• COMPS = { pipe, stopper, waterColumn},
pipe ≡ {e
1
(pipe), s
1
(pipe), s
2
(pipe)}, stopper ≡
{e
1
(stopper), s
1
(stopper), s
2
(stopper)},
waterColumn ≡ {s
1
(waterColumn)}};
• R
i
= { s
1
(waterColumn) = e
1
(pipe), s
2
(pipe) =
e
1
(stopper))} (i.e. there is two interconnection
relations);
• R
x
= { V(t) = s
1
(waterColumn), Qf(t) =
s
1
(pipe), Pr(t) = s
2
(pipe), Qs(t) = s
1
(stopper),
R(t) = s
2
(stopper)}.
The set Ψ of PM allows to define a set of 8
ranges for each variables of X(t) and consequently (i)
the set ∆ of 8 constants δ
i
of the Functional Model
FM(P(t)) (column ”range values” in the Figure 3)
and (ii) the corresponding set C of 8 discrete event
classes C
i
= {e
i
} (column ”Events” in the Figure 3).
These constants define also the set X
i
of the 17 possi-
ble values for X(t). The Structural Model SM(P(t))
and the TOS allows to eliminates 7 of these values that
are note physically possible for X(t): for example, a
value X
i
so thatV(t) = 0 and Qf = 1 is physically im-
possible. The resulting set X
i
of the 10 possible val-
ues of X(t) defines then the 10 distinguishable states
S = {s
i
} of the Behavioral Model BM(P(t)).
Variables
Constants
Range
Range Values
Events
V(t)<Vmin
0
e1:V(t)<Vmin
e2:V(t)>Vmin
e3:V(t)<Vmax
V(t)>Vmax
2
e4:V(t)>Vmax
Qs(t)<Qsmin
0
e5:Qs(t)<Qsmin
e6:Qs(t)>Qsmin
e7:Qs(t)<Qsmax
Qs(t)>Qsmax
2
e8:Qs(t)>Qsmax
Qf(t)<Qfmin
0
e9:Qf(t)<Qfmin
Qf(t)>Qfmin
1
e10:Qf(t)>Qfmin
V(t) Vmax, Vmin
Qf(t) Qfmin
Vmin<V(t)<Vmax
1
Qs(t) Qsmax, Qsmin Qsmin<Qs(t)<Qsmax
1
Figure 3: Constraint table.
Given the sets {X
i
} of 10 values and C, three ma-
trix are filled in to identify the physically possible
temporal successions:
• an event-to-event matrix E = [e
ij
] defined on E ×
E at value on {0, 1} so that e
ij
= 1 when the an
occurrence o(k) of the C
i
class can be followed
by an occurrence o(k + 1) of the C
j
class (i.e.
(o(k), o(k + 1)) is physically observable on P(t)).
• a value-to-value matrix X = [x
ij
] defined on X ×
X at value on {0, 1} so that x
ij
= 1 when a X(t)
ICSOFT 2008 - International Conference on Software and Data Technologies
254
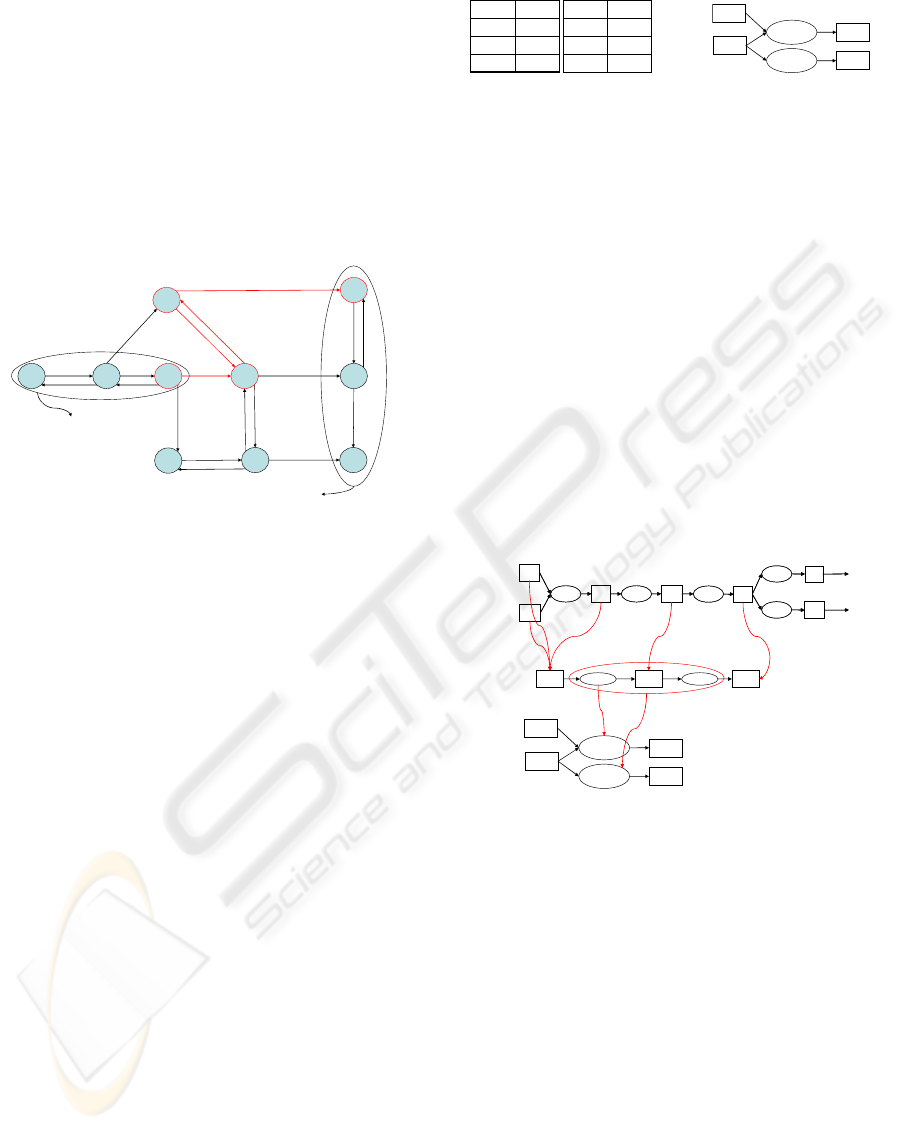
can physically move from the value X
i
at time t
k
(i.e. X(t
k
) = X
i
) to the value X
j
at the next time
t
k+1
in one occurrence of a discrete event class
(i.e. X(t
k+1
= X
j
).
• a value-to-event matrix T = [t
ij
] defined on X × X
at value on C so that t
ij
= {C
i
} is a set of discrete
event class that is not empty when there exist at
leat an occurrence of a class C
i
making the value
of X(t) moving from X
i
to X
j
in P(t).
This latter transition matrix T is deduced from the
other two matrix E and X.
X0 X1
X2
X5X4
X7
X8
X11
X14
X17
e2
e1
e3
e5
e5
e8
e4
e4
e8
e3
e6
e6
e5
e8
e2
e3
e4
e5
e6
Normal states
Awry states
Figure 4: Behavioral model and Cublize dam story.
The state graph of the Figure 4 is a graphical
representation of the T transition matrix and repre-
sents the Behavioral Model BM(P(t)) of P(t). In this
graph, a nodeis a state s
i
and a relation R(s
i
, s
j
,C
i
) be-
tween two states is labeled with a discrete event class
C
i
when C
i
∈ t
ij
. This state graph is then transformed
in an discrete event graph where a node is a class C
i
and a link is binary relation between two classes C
i
and C
j
if and only if e
ij
= 1. Next, the classes C
i
of
the nodes are replaced with the associated assignation
of the variables x
i
(t) = δ
i
according to the Stochastic
Approach framework. The resulting graph is made a
set of relations between two assignations R
ij
(x
i
(t) =
δ
i
, x
j
(t) = δ
j
). Using the sets R
x
and the R
i
of the
Structural Model SM(P(t)), the set R= { R
ij
} is made
with the relations R
ij
(x
i
(t) = δ
i
, x
j
(t) = δ
j
) that are
physically supported with an interconnection relation
= (s
i
(c
i
), e
j
(c
j
)) of R
i
. The set R is then transformed
in the set F of functions f
i
(x
1
(t), x
2
(t), ..., x
m
(t))
of the Functional Model FM(P(t)) and their corre-
sponding table of values (cf. Figure 5), and the set R
f
is then constituted (i.e. R
f
= { Qs(t) = f
1
(V(t), R(t)),
Qf(t) = f
2
(V(t))}. The R(t) variable is an internal
variable of the component ”stopper” that explains the
different values Qs(t) can take when V(t) = 1. This
is the role of the diagnosis to determine that P(t) is in
an abnormal state like X
11
for example because of the
value of R(t).
The red paths of the Behavioral Model BM(P(t))
of Figure 4 illustrates the concrete story of Cublize’s
Qf(t)V(t)
12
01
00
Qf(t)V(t)
12
01
00
Qs(t)V(t)
0,12
0,1,21
00
Qs(t)V(t)
0,12
0,1,21
00
f1
V(t)
Qs(t)
Qf(t)f2
R(t)
(a) (b)
Figure 5: Table of values and the functional model associ-
ated.
dam, that is to say the Behavioral Model BM(ω) of
the scenario model M(ω) provided in (Masse and Le
Goc, 2007). It can be see that BM(ω) ⊂ BM(P(t)):
BM(P(t)) can be used to generate a large set of
scenarios that can be used to simulate the behav-
ior and to learn to diagnose a dam. Similarly, the
Figure 6) shows the relation between the Functional
Model FM(ω) of the scenario model and the Func-
tional Model FM(P(t)) of the process P(t). The
Generic Model M(P(t)) is then an abstract descrip-
tion of the relations between the concrete variables
of Cublize dam. The experts of the Cemagref hav-
ing validated this generic model, this shows that the
TOM4D method can be used to represent a real world
set of knowledge.
f1
F2F1 F3
F4
x1
x2
x4
x3
x5
x6
x7F5
F2F1 F3
F4
x1
x2
x4
x3
x5
x6
x7F5
V(t) Qs(t) Qf(t)
Functional model of the Cublize dam translates with process variables
Functional model of the Cublize dam obtained at the first step of modeling
F2
Functional Model of the process obtained at the third step of modeling
F3
V(t)
Qs(t)
Qf(t)f2
R(t)
Figure 6: Comparison between the functional models.
5 CONCLUSIONS
This paper presents the principles of the TOM4D
methodology used to represent a process at the level
of abstraction that an Expert uses when diagnosing.
At such a level of abstraction, the number of compo-
nents is minimized so that the computational problem
of the usual diagnosis algorithm is decreased. The
TOM4D methodology represents the implicit model
of an Expert with four models: a perception, a struc-
tural, a behavioral and a functional model. These
models are linked together with the concept of vari-
able, which allows to define a way to analyze the con-
sistency between them. The methodology is directed
with the timed observations to be adequate with the
Stochastic Approach framework for discovering tem-
MODELING PROCESSES FROM TIMED OBSERVATIONS
255

poral knowledge from the timed observations con-
tained in a database. One of the main advantage of
the models of the TOM4D methodology is to be hu-
manly understandable.
The methodology is applied to a real world prob-
lem: the hydraulic dam of Cublize (France). The re-
sulting models have then been validated by the hy-
draulic dam Expert’s of the Cemagref, the French
governmental organization that assumes the security
of French hydraulic civil engineering structures. Our
current works are oriented towards the adaptation of
Reiter’s algorithm of diagnosis to timed observations
and the generalization of this modeling approach to
introduce a recursive principle of modeling.
REFERENCES
Abu-Hanna, A., Benjamins, R., and Jansweijer, W. (1991).
Device understanding and modeling for diagnosis.
IEEE Expert, 6(2):26–31.
Basseville, M. and Cordier, M.-O. (1996). Surveil-
lance et diagnostic de syst`emes dynamiques : ap-
proche compl´ementaire du traitement de signal et de
l’intelligence artificielle. Rapport.
Chittaro, L., Guida, G., Tasso, C., and Toppano, E. (1993).
Functional and teological knowledge in the multimod-
eling approach for reasoning about physical systems:
A case study in diagnosis. IEEE Transactions on sys-
tems.
Clancey, W. (1987). Heuristic classification. Artificial In-
telligence, 25(3):289–350.
Dague, P. (2001). Th´eorie logique du diagnostic `a base de
mod`eles. Diagnostic, Intelligence Artificielle et Re-
connaissance des Formes, pages 17–105.
Davis, R. (1984). Diagnostic reasoning based on structure
and behavior. Artificial Intelligence, 24:347–410.
De Kleer, J. and Brown, J. (1984). A Qualitative Physics
Confluences. Artificial Intelligence, 24:7–83.
Falkeihainer, B. and Forbus, K. D. (1988). Seting up large
scale qualitative models. In Proceedings of the 7th
National Conference of Artificial Intelligence, pages
301–306, St. Paul, MN, USA.
Falkeihainer, B. and Forbus, K. D. (1991). Compositional
modeling: Finding the right model for the job. Artifi-
cial Intelligence, 51:95–143.
Forbus, K. et al. (1984). Qualitative Process Theory. Artifi-
cial Intelligence, 24(1-3):85–168.
Franke, D. W. (1991). Deriving and using descriptions of
purpose. IEEE Expert, 6(2):41–47.
Hayes, P. (1989). Naive physics I: ontology for liquids.
Morgan Kaufmann Publishers Inc. San Francisco, CA,
USA.
Le Goc, M. (2004). Sachem, a real time intelligent diagno-
sis system based on the discrete event paradigm. Sim-
ulation, The Society for Modeling and Simulation In-
ternational Ed., 80(11):591–617.
Le Goc, M. (2006). Notion d’Observation pour le Di-
agnostic des Processus Dynamiques: Application `a
Sachem et `a la d´ecouverte de Connaissances Tem-
porelles. Hdr, Facult´e des Sciences et Techniques de
Saint J´erˆome, Marseille, France.
Le Goc, M. and B´enayadi, N. (2008). Dicovering expert’s
knowledge from sequences of discrete event class oc-
currences. In To appear in the proceedings of the 10th
International Conference on Enterprise Information
Systems (ICEIS08), Barcelona, Spain, 12-16th of June
2008.
Le Goc, M., Bouch´e, P., and Giambiasi, N. (2005). Stochas-
tic modeling of continuous time discrete event se-
quence for diagnosis. 16th International Workshop on
Principles of Diagnosis (DX’05) Pacific Grove, Cali-
fornia, USA.
Lee, W. and Kuipers, B. (1988). Non-Intersection of Trajec-
tories in Qualitative Phase Space: A Global Constraint
for Qualitative Simulation. Proceedings of the Seventh
National Conference on Artificial Intelligence, AAAI-
88, pages 286–291.
Masse, E. and Le Goc, M. (2007). Modeling dynamic
systems from their behavior for a multi model based
diagnosis. In Proceedings of the 18th International
Workshop on the Principles of Diagnosis (DX’07),
Nashville, TN, USA, May 29-31 2007.
Murthy, S. (1988). Qualitative reasoning at multiple reso-
lutions. Proceedings of the National Conference on
Artificial Intelligence, pages 296–300.
Reiter, R. (1987). A theory for diagnosis for first principles.
Artificial Intelligence, 32:57–95.
Rosenberg, R. and Karnopp, D. (1983). Introduction to
Physical System Dynamics. McGraw-Hill, Inc. New
York, NY, USA.
Schreiber, A., Akkermans, J. M., Anjewierden, A. A.,
de Hogg, R., Shadbolt, N. R., Van de Velde, W., and
Wielinga, B. J. (2000). Knowledge Engineering and
Management, The CommonKADS Methodology. MIT
Press.
Struss, P. and Dressler, O. (1989). Physical negation –
integrating fault models into the general diagnostic
engine. In Proceedings of the 11th International
Joint Conference on Artificial Intelligence (IJCAI-89),
pages 1318–1323.
Thetiot, R. (1999). Utilisation de l’Approche Multi-
mod`eles pour l’Aide au Diagnostic d’Installations In-
dustrielles. Phd in sciences, Universit´e d’Evry Val
d’Essonne, France.
Zanni, C., Le Goc, M., and Frydman, C. (2005). A con-
ceptual framework for the analysis, classification and
choice of knowledge-based diagnosis systems.
Zouaoui, F., Th´etiot, R., and Dumas, M. (1997). Multimod-
eling representation of pwr primary coolant loop. In
Proceedings Poster of International Joint Conference
on Artificial Intelligence (IJCAI-97), page 116.
ICSOFT 2008 - International Conference on Software and Data Technologies
256
