POINT MULTIPLICATION ON SUPERSINGULAR ELLIPTIC
CURVES DEFINED OVER FIELDS OF CHARACTERISTIC 2 AND 3
Kwang Ho Kim
Department of Algebra, Institute of Mathematics, The State Academy of Sciences
Pyongyang city, Democratic People’s Republic of Korea
Christophe Negre
Team DALI/ELIAUS, University of Perpignan, Perpignan, France
Keywords:
Supersingular, Eliptic Curve, Coordinate Systems, Mixed Addition, Doubling, Tripling.
Abstract:
Elliptic curve cryptosystem protocols use two main operations, the scalar multiplication and the pairing com-
putation. Both of them are done through a chain of basic operation on the curve. In this paper we present new
formulas for supersingular elliptic curve in characteristic 2 and 3. We improve best known formulas by at least
one multiplication in the field.
1 INTRODUCTION
For elliptic curve cryptosystems, scalar multiplica-
tion on the curve is the most important but time-
consuming operation. So the research on speeding up
this operation continues to get increasing attraction
since the elliptic curve cryptography has been pro-
posed (Koblitz 1987, Miller 1986).
The scalar multiplication is generally performed
by a chain of elementary curve operations like point
addition, point doubling and point tripling. This is
the case for example in double and add method (Han-
kerson et al., 2004) or triple and add method (Page
and Smart, 2002). Each curve operation requires sev-
eral field operations on the point coordinates (addi-
tion/subtraction, multiplication and eventually inver-
sion or powering).
Consequently to get an efficient scalar multiplica-
tion and an efficient pairing it is important to decrease
the number of field operations involved in basic curve
operations.
Here we focus on supersingular elliptic curve in
characteristic two and three. Projective versions of
arithmetic on supersingular elliptic curves have been
proposed in characteristic 3 by N. Koblitz (Koblitz,
1998), P. Baretto et al. (Baretto et al., 2002) and K.
Harrison et al. (Harrison et al., 2002). For character-
istic two the main result is the work et al.(Scott et al.,
2006). The cost of their respective formulas are given
in Table 1.
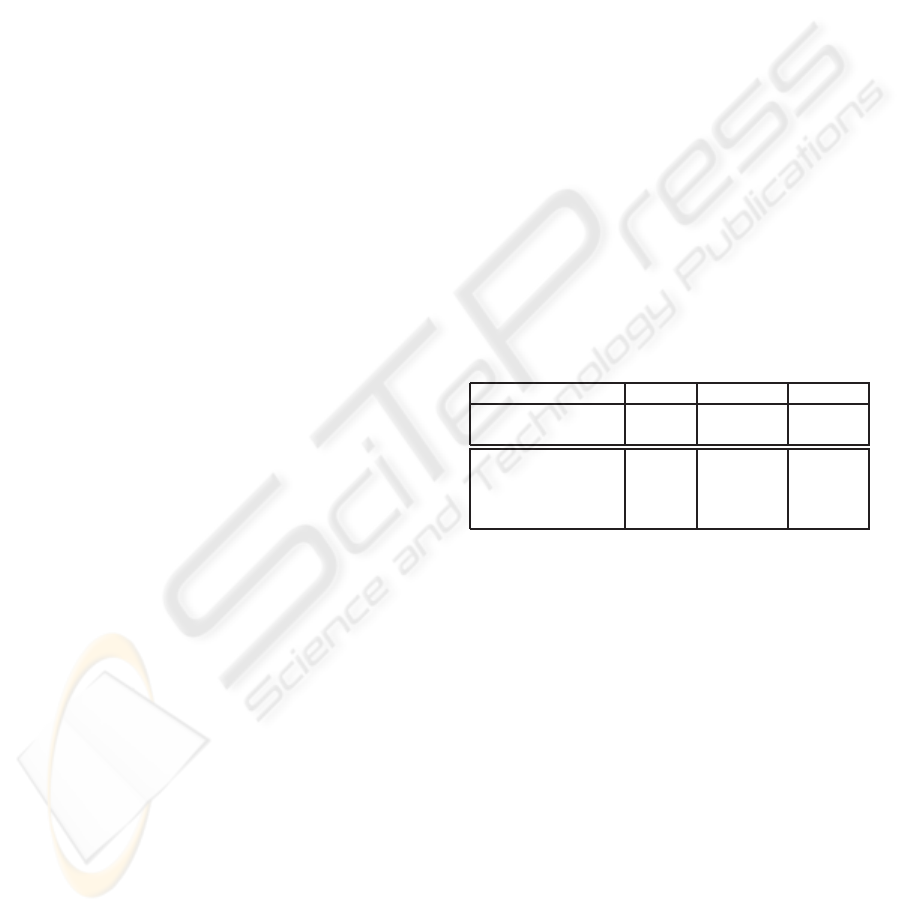
Table 1: Complexity comparison.
Method Trip. Mixed add. Doub.
(Scott et al., 2006) − 9M + 3S 1M + 7S
Proposed − 9M + 5S 8S
(Koblitz, 1998) 6C 10M + 1C
(Baretto et al., 2002) 6C 9M + 1C
(Harrison et al., 2002) M + 6C 8M + 3C 7M + 2C
Proposed 8C 7M + 3C 6M + 4C
In this paper we first propose a new coordinate
system in characteristic 2 called the XZ-projectiveco-
ordinate system. We provide in this system formulas
for doubling and mixed addition. We propose also a
new coordinate system for characteristic 3 called ML-
projectivecoordinate system. Again we give formulas
for adding, doubling and tripling. The cost of these
formulas are given in Table 1
Table 1 shows that our formulas provide some im-
provement in the efficiency of curve operations.
This paper is organizedas follows. Basic concepts
and previous work on arithmetic on supersingular el-
liptic curves are summarized in Section 2. We present
our contribution for supersingular curve in character-
istic 2 (resp. 3) in Section 3 (resp. Section 4). Finally
we briefly conclude in Section 5.
373
Ho Kim K. and Negre C. (2008).
POINT MULTIPLICATION ON SUPERSINGULAR ELLIPTIC CURVES DEFINED OVER FIELDS OF CHARACTERISTIC 2 AND 3.
In Proceedings of the International Conference on Security and Cr yptography, pages 373-376
DOI: 10.5220/0001926103730376
Copyright
c
 SciTePress

Table 2: Curve operations Affine coordinates.
Characteric2 Characteric3
Add
λ =
y
1
+y
2
x
1
+x
2
,
x
3
= λ
2
+ (x
1
+ x
2
),
y
3
= y
1
+ 1
+λ(x
1
+ x
3
),
λ =
y
1
−y
2
x
1
−x
2
,
x
3
= λ
2
− (x
1
+ x
2
),
y
3
= (y
1
+ y
2
) − λ
3
,
Doub.
x
3
= x
4
1
+ 1,
y
3
= y
4
1
+ x
4
1
λ =
1
y
1
x
3
= x
1
+ λ,
y
3
= −(y
1
+ λ
3
),
Trip. −
x
3
= x
9
1
− b,
y
3
= −y
9
1
.
2 ARITHMETIC ON
SUPERSINGULAR ELLIPTIC
CURVES
Given a finite group with underlying difficult discrete
logarithm problem (DLP) and efficient group law, one
could use this group to implement cryptographic pro-
tocols such as ElGamal encryption or Diffie-Hellman
key exchange.
Recall that given a finite field F
p
n
with p prime an
elliptic curve E over F
p
n
is the set of pairs (x,y) ∈
F
p
n
× F
p
n
satisfying a Weierstrass equation of the
form y
2
+ a
1
xy + a
3
y = x
3
+ a
2
x
2
+ a
4
x + a
6
where
a
i
for i = 1,...,6 are constants in F
p
n
. Elliptic curves
have a natural group structure given by chord and tan-
gent method. This provides efficient group arithmetic
and difficult DLP suitable for cryptographic applica-
tions.
In this paper we consider special elliptic curves,
the supersingular elliptic curves defined over field of
characteristic 2 and 3. Their equation are the follow-
ing
E(F
2
n
) Y
2
+Y = X
3
+ X + b where b ∈ {0, 1} (1)
E(F
3
n
) Y
2
= X
3
− X + b where b ∈ {−1,1} (2)
These curves are really interesting for efficient im-
plementation of pairing-based cryptosystems. Indeed,
to implement protocol based on pairing on an elliptic
curve E(F
q
), the curve must have an embedded de-
gree k not too big. The embedded degree is the small-
est integer k such that the Tate pairing, for instance,
can be computed. It has been shown that supersin-
gular elliptic curves satisfy this condition (Galbraith,
2001).
In affine coordinates, operations on the curve can
be computed using the following formulas give in Ta-
ble 2
Since the proposition of ECC by Koblitz and
Miller, research have been done to improvethe cost of
operations on the curve. We see in Table 2 that dou-
bling and tripling is free of field inversion and field
multiplication. But the other operations require inver-
sion in affine coordinate.
A popular idea to avoid inversion in curve opera-
tions consists to use projective coordinates. The most
interesting projective systems are the following
1. Ordinary projective (X,Y, Z) ↔ (x,y) =
(X/Z,Y/Z) in affine.
2. Lopez-Dahab projective (X,Y, Z) ↔ (x,y) =
(X/Z,Y/Z
2
) in affine.
3. Jacobian projective (X,Y,Z) ↔ (X/Z
2
,Y/Z
3
)
Each system provides different operation cost for
addition, doubling and tripling, but all of them avoid
field inversion. Mixed addition is simply an addition
with a point in the current projective system say P
1
and a second point P
2
in affine coordinate. It is gener-
ally cheaper than a general addition.
Field operations. Let us denote I a field inversion,
M a multiplication, S a squaring and C a cubing in
the ground field. These operations have different
time consuming depending on the characteristic of the
field. Specifically
• In characteristic two we have I ≫ M ≫ S and C =
M + S.
• In the case of characteristic three we have I ≫
M
∼
=
S ≫ C (see (Ahmadi et al., 2007)).
The curve operations are optimized regarding these
relative costs of field operations.
3 OPERATIONS IN
CHARACTERISTIC 2
In this section we present our work concerning arith-
metic on an supersingular elliptic curve in characteris-
tic 2. Specifically we would like to improve the arith-
metic on the curve
E(F
2
n
) Y
2
+Y = X
3
+ X + b where b ∈ {0,1}.
To reach this goal we use a new system of repre-
sentation called XZ-projective coordinates. This sys-
tem can be seen as an improvement of the Lopez-
Dahab (Lopez and Dahab, 1998) projective coordi-
nates.
Definition 1 (XZ-projective coordinates). The XZ-
projective coordinates of a point P on an elliptic curve
E is a quadruple (X,Y,Z,T) such that T = XZ and
the affine coordinate (x,y) of P are given by
x = X/Z, y = Y/Z
2
.
SECRYPT 2008 - International Conference on Security and Cryptography
374

In this system we obtain the formulas given in the
following proposition for addition and doubling on
the curve defined by (1).
Proposition 1 (Curve operation in XZ-projective co-
ordinate). Let E(F
2
n
) a supersingular curve defined
by the following equation
Y
2
+Y = X
3
+ X + b where b ∈ {0,1}.
Let P
1
= (X
1
,Y
1
,Z
1
,T
1
) and P
2
= (X
2
,Y
2
,1,T
2
=
X
2
) be two points on E(F
2
n
) expressed in XZ-
projective coordinates. Then
Mixed Addition. Let P
3
= P
1
+ P
2
, the XZ-
coordinates (X
3
,Y
3
,Z
3
,T
3
) of P
3
can be computed
as
Z
3
= (X
2
Z
2
1
+ T
1
)
2
, T
3
= X
3
Z
3
,
X
3
= (X
2
Z
2
1
+ T
1
)(X
2
Z
1
+ X
1
)
2
+(Y
2
Z
2
1
+Y
1
)
2
,
Y
3
= Z
2
3
(Y
2
+ 1)
+(X
2
Z
3
+ X
3
)(X
2
Z
2
1
+ T
1
)(Y
2
Z
2
1
+Y
1
).
(3)
And the cost of these formulas is 9M + 3S
Doubling. Let P
3
= 2P
1
, the XZ-coordinates
(X
3
,Y
3
,Z
3
,T
3
) of P
3
can be computed as
X
3
= (X
1
+ Z
1
)
4
, Y
3
= (Y
1
+ T
1
)
4
,
Z
3
= (Z
2
1
)
2
, T
3
= (T
1
+ Z
2
1
)
4
.
(4)
The cost of these formulas is equal to 8S.
Proof. Mixed Addition. To provethat the formulas(3)
are correct, we have to provethat X
3
/Z
3
andY
3
/Z
2
3
are
equal to the expression of x
3
and y
3
in Table 2. Using
(3) we have
X
3
/Z
3
=
(X
2
Z
2
1
+ T
1
)(X
2
Z
1
+ X
1
)
2
+ (Y
2
Z
2
1
+Y
1
)
2
(X
2
Z
2
1
+ T
1
)
2
.
If we factorize Z
4
1
in the numerator and the denomi-
nator we get
X
3
/Z
3
=
(X
2
+X
1
/Z
1
)(X
2
+X
1
/Z
1
)
2
+(Y
2
+Y
1
/Z
2
1
)
2
(X
2
+X
1
/Z
1
)
2
= (x
2
+ x
1
) +

y
2
+y
1
x
2
+x
1

2
.
This means that X
3
/Z
3
satisfies equation of Table 2.
Now let do the same thing in the expression of Y
3
/Z
2
3
Y
3
/Z
2
3
= (Y
2
+ 1) +
(X
2
+X
3
/Z
3
)(X
2
Z
2
1
+T
1
)(Y
2
Z
2
1
+Y
1
)
Z
3
= (Y
2
+ 1) +
(X
2
+X
3
/Z
3
)(X
2
+X
1
/Z
1
)(Y
2
+Y
1
/Z
2
1
)
(X
2
+X
1
/Z
1
)
2
but this last expression is equal the expression of Ta-
ble 2.
Doubling. This case is simpler, and the proof is sim-
ilar to the proof of addition formulas. For the sake of
simplicity we leave this part to the reader.
Now let us compare our formulas with best known
formulas for curve E(F
2
n
defined by
Y
2
+Y = X
3
+ X + b where b ∈ {0, 1}.
We reported the cost of these formulas (Scott et al.,
2006) reported in Table 3.
Table 3: Complexity comparison.
Algorithm Coord. Doubling Mixed add
Classic Aff. 4S I + 2M + S
(Scott et al., 2006) Jac. M + 7S 9M + 3S
Proposed XZ-proj. 8S 9M + 5S
We can see that the doubling is cheaper by 1M
compared to Scott. In counter part,we have one more
squaring int the doubling, and two more squaring in
the addition.
4 OPERATIONS IN
CHARACTERISTIC 3
We propose a novel system of representation called
ML-projective coordinates. This system can be seen
as an improvement of the original Jacobian coordi-
nate.
Definition 2. The ML-projective coordinate of a point
P on an elliptic curve E is quadruplet (X,Y,Z,T)
such that T = Z
2
and the affine coordinate (x,y) of
P are given by
x = X/T,y = Y/Z
3
.
In this system we found different formulas for
point addition, point doubling and point tripling on
an elliptic curve defined by (2).
Proposition 2 (Curve operation in ML-projective co-
ordinate). Let E(F
3
n
) a supersingular curve defined
by the following equation
E(F
3
n
) Y
2
= X
3
− X + b where b = ±1
Let P
1
= (X
1
,Y
1
,Z
1
,T
1
) and P
2
= (X
2
,Y
2
,1,1) be
two points on E(F
3
n
) expressed in ML-projective co-
ordinates. Then
Addition. Let P
3
= P
1
+ P
2
, the ML-coordinates
(X
3
,Y
3
,Z
3
,T
3
) of P
3
can be computed as
Z
3
= Z
1
(X
2
T
1
− X
1
), T
3
= Z
2
3
,
X
3
= (Y
2
Z
3
1
−Y
1
)
2
+ (X
2
T
1
− X
1
)
3
+X
2
T
3
,
Y
3
= (Y
2
Z
3
1
+Y
1
)(X
2
T
1
− X
1
)
3
−(Y
2
Z
3
1
−Y
1
)
3
.
(5)
These formulas require 7M + 3C.
POINT MULTIPLICATION ON SUPERSINGULAR ELLIPTIC CURVES DEFINED OVER FIELDS OF
CHARACTERISTIC 2 AND 3
375

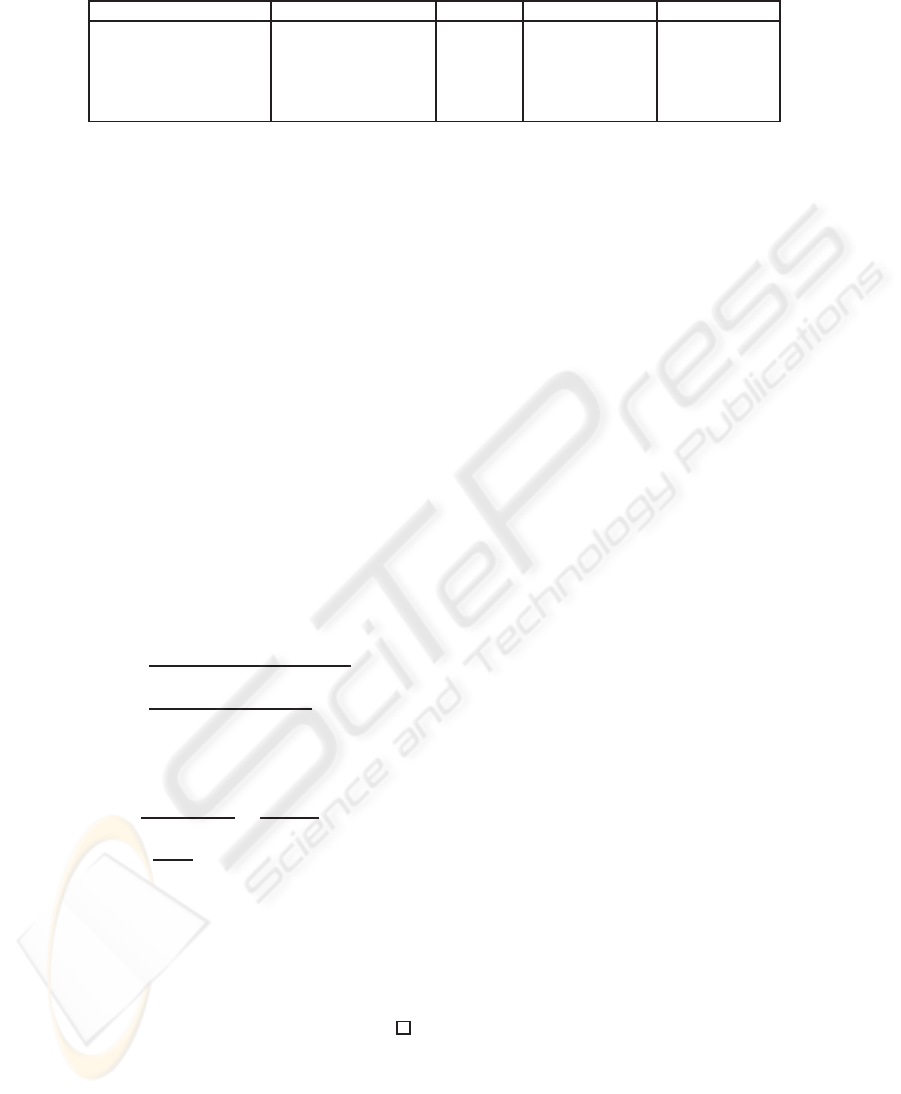
Table 4: Complexity comparison.
Algorithm Coordinates Tripling Mixed addition Doubling
Classic Affine 4C 1I + 2M + 1C 1I + 1M + 1C
(Koblitz, 1998) Ordinary projective 6C 10M + 1C -
(Baretto et al., 2002) Ordinary projective 6C 9M + 1C -
(Harrison et al., 2002) Jacobian 1M + 6C 8M + 3C 7M + 2C
Proposed ML-Projective 8C 7M+ 3C 6M + 4C
Doubling. Let P
3
= 2P
1
the ML-coordinates
(X
3
,Y
3
,Z
3
,T
3
) of P
3
can be computed as
Z
3
= −Y
1
Z
3
1
, T
3
= Z
2
3
,
X
3
= (T
3
1
)
2
+ (X
3
1
−Y
2
1
)Y
2
1
+ bT
3
,
Y
3
= T
9
1
+Y
2
1
T
3
.
(6)
These formulas require 6M + 4C.
Tripling. Let P
3
= 3P
1
the ML-coordinates
(X
3
,Y
3
,Z
3
,T
3
) of P
3
can be computed as
X
3
= (X
1
− bT
1
)
9
, Y
3
= −Y
9
1
,
Z
3
= Z
9
1
, T
3
= T
9
1
.
(7)
These formulas require 8C.
Proof. Mixed Addition. Let us check that X
3
/T
3
and
Y
3
/Z
3
3
are equal respectively to x
3
and y
3
of Table 2.
For X
3
/T
3
we have
X
3
/T
3
=
(Y
2
Z
3
1
−Y
1
)
2
+(X
2
T
1
−X
1
)
3
+X
2
T
3
T
3
=
(Y
2
Z
3
1
−Y
1
)
2
+(X
2
Z
2
1
−X
1
)
3
(
Z
1
(X
2
Z
2
1
−X
1
)
)
2
+ X
2
since T
1
= Z
2
1
. We proceed the simplifications
X
3
/T
3
=
(Y
2
Z
3
1
−Y
1
)
2
Z
2
1
(X
2
Z
2
1
−X
1
)
2
+
X
2
Z
2
1
−X
1
Z
2
1
+ X
2
=

y
2
−y
1
x
2
−x
1

2
− (x
2
+ x
1
).
After the cancellation of the power of Z
1
in the
numerators and denominators we get the required ex-
pression (Table 2).
ForY
3
/Z
3
3
and for Doubling and Tripling formulas
we can prove it in the same way.
In Table 4 we give the cost of the operation in ML-
coordinate and also the cost of the best known for-
mulas ((Koblitz, 1998; Baretto et al., 2002; Harrison
et al., 2002)). We remark that our formulas improve
previous mixed addition formulas by 1M or 2M. In
on other hand, the tripling require 2 more cubing.
5 CONCLUSIONS
In this paper we have studied the arithmetic on super-
singular elliptic curve defined over field of character-
istic 2 and 3. We have introduced two new coordinate
systems , the XZ-projective coordinates and the ML-
projective coordinates. We obtain new formulas for
point addition, point doubling and point tripling on
the curve. The formulas are cheaper and provide a
more efficient scalar multiplication on the curve.
REFERENCES
Ahmadi, O., Hankerson, D., , and Menezes, A. (2007).
Software implementation of arithmetic in GF(3
n
). In
WAIFI 2007.
Baretto, P. S. L. M., Kim, H. Y., Lynn, B., and Scott, M.
(2002). Efficient algorithms for pairing based cryp-
tosystems. In CRYPTO’2002, volume 2442, pages
354–368.
Galbraith, S. D. (2001). Supersingular curves in cryptogra-
phy. Lecture Notes in Computer Science, 2248.
Hankerson, D., Menezes, A., and Vanstone, S. (2004).
Guide to Elliptic Curve Cryptography. Springer-
Verlag.
Harrison, K., Page, D., and Smart, N. P. (2002). Software
implementation of finite fields of characteristic three,
for use in pairing-based cryptosystems. LMS J. Com-
put. Math., 5:181–193.
Koblitz, N. (1998). An elliptic curve implementation of the
finite field digital signature algorithm. In CRYPTO’98,
volume 1462, pages 327–337.
Lopez, J. and Dahab, R. (1998). Improved algorithms for
elliptic curve arithmetic in GF(2
n
). In SAC’98, pages
201–212.
Page, D. and Smart, N. P. (2002). Hardware implemen-
tation of finite fields of characteristic three. In 4th
CHES’2002, volume 2523 of LNCS, pages 529–539.
Springer.
Scott, M., Costigan, N., and Abdulwahab, W. (2006). Im-
plementing cryptographic pairings on smartcards. In
CHES 2006, volume 4249, pages 134–147.
SECRYPT 2008 - International Conference on Security and Cryptography
376