
Elements of a Gestalt Algebra: Steps Towards
Understanding Images and Scenes
Eckart Michaelsen, Michael Arens and Leo Doktorski
FGAN-FOM, Gutleuthausstrasse 1, 76275 Ettlingen, Germany
Abstract. A mathematical structure is sketched that is meant to capture the
regularities and hierarchies in the structure of images. The approach is moti-
vated by difficulties arising from aerial image analysis of urban terrain. It is not
feasible to list and model all possibilities for things such as buildings that occur
in such data. Emanating from the Gestalt-theory of perception an abstract alge-
bra of operations on image objects is defined and the formal properties are dis-
cussed. It is intended to build a future software system on such formalisms that
will realize only those gestalt models that are evident from the data and can
build and recognize structures of previously unseen and unexpected structure.
1 Introduction
At least since the days of Helmholtz the underlying principles of human perception
are scientifically discussed. Major contributions are now a hundred years old. The
German word Gestalt is the usual term referring to groups of entities arranged in a
salient manner. Salience is meant here as the property of inevitably guiding human
perceptive attention.
Figure 1 shows an example for situations that we intend with this contribution. In an
aerial image of an urban area symmetric gabled roofs are present. A building is
formed of two wings of the same form rotated by π/2. Such building is arranged pair-
wise in a mirror-symmetry. More building groups of this type are arranged in a row.
The row again has a symmetric partner, etc.
How may a machine-vision system look like that can recognize such a pattern and
generate an appropriate description from it? It will be only of practical use, if it does
not code the particular realizations in this picture rigidly. It must be flexible to dis-
cover new arrangements and hierarchies in every example. What kinds of data-
structures are suitable for such task? These are the topics of the proposed rather pre-
liminary contribution of ideas.
Michaelsen E., Arens M. and Doktorski L. (2008).
Elements of a Gestalt Algebra: Steps Towards Understanding Images and Scenes.
In Image Mining Theory and Applications, pages 65-73
DOI: 10.5220/0002339200650073
Copyright
c
SciTePress
2 Related Work
Progress in this field is slow and thus quite old literature is to be considered. Some of
it has been originally published in different languages and is only partially available
in English translations.
2.1 Gestaltism
The classics of Gestaltist literature are [20], [14] and [6]. A common practice in this
branch of psychology is argumentation by drawing dot patterns and demonstrating the
gestalt phenomena by use of the readers own perceptive mechanisms. A lot of work
consists of identifying or inventing illusions that reveal properties of human percep-
tion.
Steps towards incorporating such findings into automatic machine vision systems are
taken e.g. by Lowe [7]. Often this involves a more or less general theory of percep-
tion incorporating machines, animals and human [3]. Probably the most elaborated
work on the mathematical foundation and automation of Gestaltist ideas is [1].
.
.
.
.
.
.
.
.
.
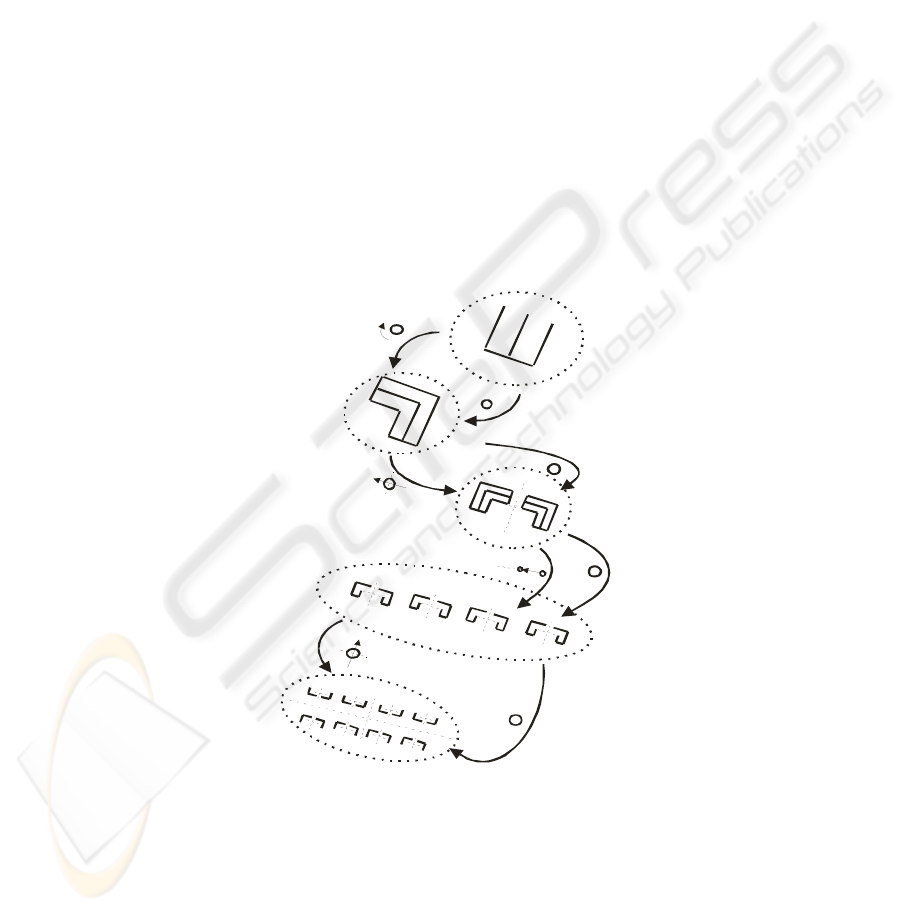
Fig. 1. Example of a rather typical Gestalt hierarchy as they occur in urban remote sensing data.
6666

2.2 Practical Attempts on Remote Sensing Data
The main interest in automatic understanding of previously unseen repetitive or sym-
metric gestalts comes from remote sensing – in particular from aerial image analysis
of urban scenery. Well known sources are the proceedings of the ETH workshops on
building and road recognition in Ascona [4] (1995, 1997 and 2001). Elements of a
syntactic formulation of generic building models for recognition in aerial imagery can
be found e.g. in [2].
Very interesting early work on arrangements and hierarchies of arrangements of ob-
jects in aerial images is presented already 1980 by Nagao and Matsuyama [15]. The
most well known contribution concerning a corresponding production system is the
SIGMA-system [10]. There sophisticated control structures are given that can help
handling the inevitable computational effort problems.
2.3 Algebra
There is an algebraic theory of pattern recognition, image analysis and estimation
Zhuravlev and Gurevich [21,5]. Searching images for regularities of arbitrary form is
identified by Gurevich in [5] as one of the objectives of image analysis for which the
descriptive algebraic approach is meant. However, this is only one of many other
purposes – whereas this contribution focuses on this particular and important task.
The symmetry groups and grid structures used here may well be understood as par-
ticular allowable transforms in the image formation models used in the descriptive
image algebra theory. But, for the purpose of our gestalt operations, such group trans-
forms are always understood locally with respect to a specific location (and orienta-
tion). They only act on few gestalts involved in the construction – not globally. What
is found about reductions to recognizable canonical representatives may well be
transferred and used here.
Less relatedness can be found with the image algebra as defined by Ritter and Wil-
son [16]. Much of that work is related to the pixel grid structure of images, how con-
volution filters and morphological filters can be captured algebraically etc. Our ge-
stalt algebra leaves the level of pixels as soon as possible. In the extreme case a single
pixel is a primitive gestalt object of our structure – the grid is neglected and the whole
image is not treated at all.
2.4 Picture Grammars
There is a long history of syntactic pattern recognition methods. Many kinds of gram-
mars for image analysis were already studied by Rosenfeld [17]. Viewing the objects
as a set and the interrelation between them as constraints and hierarchical construc-
tions is captured by the constrained multi-set grammars of Marriot and Meyer [9].
This gains algebraic structure with Wang’s thesis [19] where e.g. mathematical order
structures are treated on the constraints between the objects. Most of these syntactical
works concentrate on certain diagram understanding tasks – such as electronic cir-
cuits.
6767

2.5 Own Previous Work
Resting on earlier fundaments the blackboard image understanding system from
which many of the ideas of this contribution stem was first published in 1986 [8].
There has been a syntactic foundation as well [12]. The system was used for complex
3D-scene understanding tasks [18]. Later work with the same production system
structure was on building recognition from high resolution SAR-images [11] and on
estimation of geometric entities by good sample consensus [13]. Up to now there has
not been an algebraic fundament to this work. And up to now the symbols and object-
classes had been fixed and pre-defined. The purpose of this contribution is initializing
new work in these directions.
3 Definitions
This technical section defines the gestalt algebra in four steps: First in Section 3.1 the
primitive elements are introduced that form the fundament of the proposed structure.
These primitives are located in a metric space. Then symmetry groups are introduced
in 3.2 working on the associated space – such that the objects can be mapped on each
other. These mappings define a matching assessment for groups of objects. Thus the
fundament is given for the gestalt operations given in 3.3 and the algebra in 3.4.
3.1 Primitive Gestalts
We call a metric space D – such as the 2d-pixel coordinates of an image, gradients of
image edges, 3d-world coordinates of laser measured scene surface points, 2d+t co-
ordinates of a video etc. – a primitive domain. On this we will build our algebraic
structure.
In order to distinguish more than one type of objects we introduce a finite set of
primitive symbols V
p
={
σ
1
,…,
σ
m
}. Each of these has a sub-space D
j
⊆
D assigned to it.
Pixels will only have their coordinates and their brightness; edgels will have a gradi-
ent instead of the brightness, etc.
Each object has an assessment value 0<α
≤
1 assigned to it. For a contour primitive
this may be a monotone function of the local gradient magnitude, etc.
An instance g=(
σ
j
, d, α)
∈
V
p
×
D
j
×
(0,1] will be called a primitive gestalt hence-
forth.
3.2 Symmetries on the Domain
A symmetry group is a finite (order m) group G of mappings f such that
:fD D→
(1)
6868

is objective and preserves the metric. G contains the identity as neutral element and
an inverse
f
-1
for every element. Examples are mirror mappings or rotations.
Such mappings have a reference frame associated with them – i.e. a position
γ
p
and
an orientation
γ
o
. Let d
0
,…,d
k
be a set of points in D with k<m. Then the minimiza-
tion problem
0
1
min | ( )|
k
ii
i
err d f d
γ
=
=−
∑
(2)
is usually straightforwardly solvable. From such a solution we can obtain a new as-
sessment using
2
01
err
e
ς
α
−⋅
<
=≤
(3)
with a suitable domain-dependent parameter ζ.
We also calculate the distance between the reference position γ
p
and the position d
0
and call it γ
d
. Thus we get for such a set of points and such a group a unique result (α,
γ
p
, γ
o
, γ
d
). We cannot recover the original points from this description – but we can
draw an “ideal representative” in the correct position, orientation and size. And we
have assessed its quality.
3.3 Gestalt Operations
As operations on gestalts
g
i
we allow symmetry operations, grid operations and clus-
ter operations:
A symmetry operation has the following form:
()
1
(,,),( , , ),
k
Gi pod
i
gh Gk
σ
γγγ α
=
⊗==
(4)
where
G is a finite symmetry group operating on D,
γ∈
G minimizes the metric dis-
tances as outlined in Section 3.2. As an example we take mirror symmetries where
k=2 and we can write
()
1211 22
(,) ( , )
( , ,2),( , , ,),
Mir Mir
pod
gg d d
hMir
σ
σ
σγγγα
⊗= ⊗ =
==
(5)
such that
γ
gives the optimal symmetry axis minimizing the metric distance between
gestalt
g
1
and its mirrored partner gestalt g
2
. It also gives the central position on the
axis and sets it on the first attribute position, where all objects have their reference
location. Other possibilities are rotation groups etc.
A grid operation has following two forms:
6969

1211 12
12
312
(,) (, )
( , ,2),( , ),
2
Grid Grid
gg d d
dd
gGrid dd
σ
σ
σ
α
⊗= ⊗ =
+
⎛⎞
=−
⎜⎟
⎝⎠
(6)
is initially grouping a pair of similar gestalts and attributing it with the corresponding
centre of gravity and translational vector respectively. This vector can be coded as an
orientation and a length. The assessment is based on the similarity of the pair of ge-
stalts. The second form is
112
12 2
(( , , ), , ) ( , )
(,,1),( , ),
11
Grid k
Grid k d t d
kd d kt
Grid k
kk
σ
σ
δ
σ
α
+
⊗
=
++
⎛⎞
=+
⎜⎟
++
⎝⎠
(7)
for recursively appending further elements to a grid with k similar gestalts so that they
form a grid with k+1 members. The centre of gravity is than shifted accordingly and
δ
2
is the estimation for the translation vector from the last gestalt of the row to the
appended gestalt. The assessment is based on the similarity of the translations
t-
δ
2
.
Note that in operation (7) the nature of the attribute domain of the first element and of
the resulting element is the same.
We would see the operations indicated in (6) and (7) only as the simplest case (1-
dimensional) of more elaborated (n-dimensional) grids known in algebraic geometry.
A cluster operation has the following form:
1
1
...
(,,),( ),
k
k
Ci
i
dd
gh Ck
k
σ
α
=
++
⎛⎞
⊗==
⎜⎟
⎝⎠
(8)
where all the gestalts
g
j
are just merged into one. This is the simplest form. There are
no further dimensions added to the attribute domain. The assessment
α is based on the
similarity and closeness of the gestalts that participate.
3.4 Closure
The closure of the operations indicated in Section 3.3 given the set of primitive ge-
stalts as sketched in Section 3.1 will be called a gestalt algebra. An element of such
algebra codes a set of primitive objects and a chain of operations on them that explain
their arrangement in the domain.
There is a problem with this: For closing the algebra the operations must be defined
for combinations of any elements of it.
• The centre-of-gravity assignment and the metric must be defined for different
primitive gestalts. One solution here may be taking into account the most
primitive common part only. E.g. for a primitive line segment and a primitive
spot element take the distance of their centres. However, this would not meet
the intention. A better solution in this case is taking this distance and adding
7070

the maximal distance possible between the orientations of line segments. Then,
a line and a spot can never have zero distance – which is intended – but their
locations still matter.
• We have seen that e.g. with every symmetry- operation the attribute domain is
gaining further dimensions. A metric is required that is also defined between
elements of spaces of different dimension and topology as they occur in the
definitions of Section 3.3. Such metric should incorporate properly the dis-
similarity between gestalts of different type and level of abstraction.
• Another possibility would be to include a special symbol “clutter” – a kind of
null. If objects are too dissimilar to give a proper metric distance their combi-
nation in an operation will result in such an object which has infinite distance
from anything else and can produce nothing else but again clutter.
Because we are aware of this technical imperfection we would not call this contri-
bution “The Gestalt algebra” but rather present it as elements of a definition of such
structure. It is not yet complete.
It is however already quite clear that many nice and desirable properties such as
associativity are not given here. Commutativity holds for certain symmetry opera-
tions. It remains to be investigated what kind of distributivity laws hold when the
different operations are mixed in compound structures.
4 Discussion
Why do we use algebraic terms and notations for the indicated purpose of describing
hierarchically constructed pattern structures? Alternatively one could also use syntac-
tic definitions such as graph-grammars or constrained multi-set grammars. In fact this
has also been done as indicated in Section 2.
Our hope is that with the help of the well developed algebraic apparatus – such as
the hierarchies of group theory – in particular ambiguous gestalts such as the one
presented in Figure 2 can be handled more appropriately. This gestalt can be com-
posed at least in the following different ways:
1) As a mirror symmetric pair of complete rotations of order four of square ge-
stalts. 2) As a mirror symmetry of two rows of four square each where also
the spacing is similar. 3) As mirror symmetry of mirror symmetry gestalts.
Fig. 2. Example of an ambiguous gestalt.
7171

If it is so which of these should really be taken as different gestalts – and which
should really be identified as the same element of our algebra? If such identification
makes sense then what is the canonical representative of such an equivalence class?
We intend to construct our formalisms such that structure, geometric attributes and
hierarchy of previously unseen objects become explicit in the automatically extracted
instances. It is most important that it can identify automatically different but equiva-
lent descriptions of the same object. We think that algebra is a good candidate to
work on these practically very important issues.
5 Conclusions
We have not shown any results on particular remote sensing applications in this con-
tribution. Also there seem to be some details and proofs missing - e.g. for the unique-
ness of the solutions of the minimization associated with each step. Both goals need
to be addressed in future: 1) Lay the theoretical fundament for the Gestalt algebra by
means of definitions and possibly theorems; 2) code elements of this structure and
test them on relevant recognition scenarios.
References
1. Desolneux, A.: Evénements significatifs et applications à l'analyse d'images. PhD thesis,
http://www.math-info.univ-paris5.fr/~desolneux/papers/these2.pdf (2000)
2. Fuchs, F.: Building Reconstruction in Urban Environment: A Graph-based Approach. In:
Baltsavias, E. P., Gruen, A., Van Gool, L. (eds.): Automatic Extraction of Man-Made Ob-
jects from Aerial and Space Images III. Birkhäuser Verlag, Basel (2001) 205-215
3. Guo, C.-E., Zhu, S.C., Wu, Y. N.: Modelling Visual Patterns by Integrating Descriptive
and Generative Methods, IJCV, 53 (1), (2003) 5-29
4. Gruen, A., Kuebler, O., Agouris, P. (eds.): Automatic Extraction of Man-Made Objects
from Aerial and Space Images. Birkhäuser Verlag, Basel (1995)
5. Gurevich, I. B.: Image Mining via Descriptive Approach. I. General Methodology and
Basic Instruments. OGRW-7-2007. To appear in Pattern Recognition and Image Analysis
(2008)
6. Kanisza, G.: Grammatica del Vedere. Il Mulino, Bologna (1980)
7. Lowe, D.: Perceptual Organization and Visual Recognition, Kluwer Academic Publishers,
Boston (1985)
8. Lütjen, K.: Ein Blackboard-basiertes Produktionssystem für die automatische
Bildauswertung. In: Hartmann, G. (ed.): Mustererkennung 1986, 8. DAGM-Symposium,
Informatik-Fachberichte 125, Springer, Berlin (1986) 164-168
9. Marroitt, K., Meyer, B. (eds.): Visual Language Theory. Springer--Verlag, Berlin (1998)
10. Matsuyama, T., Hwang, V. S.-S.: Sigma a Knowledge-based Image Understanding System.
Plenum Press, New York (1990)
11. Michaelsen E., Soergel U., Thoennessen U.: Perceptual Grouping in Automatic Detection
of Man-Made Structure in high resolution SAR data. Pattern Recognition Letters.27 (4),
(2006) 218-225
7272

12. Michaelsen. E.: Über Koordinaten Grammatiken zur Bildverarbeitung und Szenenanalyse.
Phd.. Thesis, University of Erlangen-Nürnberg, Chair of Pattern Recognition,
http://www.exemichaelsen.de/Michaelsen_Diss.pdf (1998)
13. Michaelsen, E., von Hansen, W., Kirchhof, M., Meidow, J., Stilla, U.: Estimating the
Essential Matrix: GOODSAC versus RANSAC. ISPRS Symposium on Photogrammetric
Computer Vision (PCV 2006), proceedings on CD, (2006)
14. Metzger, W.: Gesetze des Sehens. Waldemar Kramer, Frankfurt (1975)
15. Nagao, M., Matsuyama T.: A Structural Analysis of Complex Aerial Photographs, Plenum
Press. New York (1980)
16. Ritter, G. X., Wilson, J. N.: Handbook of Computer Vision Algorithms in Image Algebra.
CRC Press, New York (1996)
17. Rosenfeld, A.: Picture Languages. Academic Press, New York (1979)
18. Stilla U., Michaelsen E.: Semantic modelling of man-made objects by production nets. In:
Gruen A, Baltsavias EP, Henricsson O (eds) Automatic extraction of man-made objects
fromaerial and space images (II). Birkhäuser Verlag, Basel (1997) 43-52
19. Wang D.: Studies on the Formal Semantics of Pictures. PhD. Thesis, University of Amster-
dam, ILLC Dissertation Series, Amsterdam (1995)
20. Wertheimer, M.: Untersuchungen zur Lehre der Gestalt, II. Psychologische Forschung, 4
(1923) 301-350
21. Zhuravlev, Yu. I.: An Algebraic Approach to Recognition or Classification Problems.
Pattern Recognition and Image Analysis, 8(1) (1998) 59–100
7373
