CLASSIFYING AYURVEDIC PULSE SIGNALS VIA CONSENSUS

LOCALLY LINEAR EMBEDDING

Amod Jog, Aniruddha Joshi, Sharat Chandran

Dept. of Computer Science and Engineering, Indian Institute of Technology Bombay, Powai, Mumbai- 400076, India

Anant Madabhushi

Dept. of Biomedical Engineering, Rutgers University, Piscataway, NJ 08854, U.S.A.

Keywords:

Pulse diagnosis, Nonlinear dimensionality reduction, Time series analysis, C-LLE, LLE, Isomap, Mutual

information, Relative entropy.

Abstract:

In this paper, we present a novel method for analysis of Ayurvedic pulse signals via a recently developed non-

linear dimensionality reduction scheme called Consensus Locally Linear Embedding (C-LLE). Pulse Based

Diagnosis (PBD) is a prominent method of disease detection in Ayurveda, the system of Indian traditional

medicine. Ample anecdotal evidence suggests that for several conditions, PBD, based on sensing changes in

the patient’s pulse waveform, is superior to conventional allopathic diagnostic methods. PBD is an inexpen-

sive, non-invasive, and painless method; however, a lack of quantiﬁcation and standardization in Ayurveda,

and a paucity of expert practitioners, has limited its widespread use. The goal of this work is to develop

the ﬁrst Computer-Aided Diagnosis (CAD) system able to distinguish between normal and diseased patients

based on their PBD. Such a system would be inexpensive, reproducible, and facilitate the spread of Ayurvedic

methods. Digitized Ayurvedic pulse signals are acquired from patients using a specialized pulse waveform

recording device. In our experiments we considered a total of 50 patients. The 50 patients comprised of two

cohorts obtained at different frequencies. The ﬁrst cohort comprised 24 patients that were normal or diseased

(slipped disc (backache), stomach ailments) while the second consists of a set of 26 patients who were nor-

mal or diseased (diabetic, with skin disorders, slipped disc (backache) and stress related headaches). In this

study, we consider the C-LLE scheme which non-linearly projects the high-dimensional Ayurvedic pulse data

into a lower dimensional space where a consensus clustering scheme is employed to distinguish normal and

abnormal waveforms. C-LLE differs from other linear and nonlinear dimensionality reduction schemes in that

it respects the underlying nonlinear manifold structure on which the data lies and attempts to directly estimate

the pairwise object adjacencies in the lower dimensional embedding space. A major contribution of this work

is that it employs non-Euclidean similarity measures such as mutual information and relative entropy to esti-

mate object similarity in the high-dimensional space which are more appropriate for measuring the similarity

of the pulse signals. Our C-LLE based CAD scheme results in a classiﬁcation accuracy of 80.57% using rela-

tive entropy as the signal distance measure in distinguishing between normal and diseased patients for the ﬁrst

cohort, based on their Ayurvedic pulse signal. For the 500Hz data we got a maximum of 88.34% accuracy

with C-LLE and relative entropy as a distance measure. Furthermore, C-LLE was found to outperform LLE,

Isomap, PCA across multiple distance measures for both cohorts.

1 INTRODUCTION

Diagnosis of bodily disorders by the analysis of

the arterial pulse techniques has been practised in

Ayurveda, a system of traditional Indian medicine. It

is believed that the functioning of the human body

is governed by three humors, vata, pitta and kapha,

together known as Tridosha. The Tridosha is ana-

lyzed by obtaining the pulse waveform observed at

the three positions on the wrist. The imbalances in

Tridosha pressure waveforms are sensed by the prac-

titioner who then identiﬁes the presence and location

of the disorders in the body (Lad, 2005). Anecdotal

evidence strongly suggests that traditional Ayurvedic

pulse diagnosis is able to identify certain ailments,

such as stomach disorders and maladies in some preg-

388

Jog A., Joshi A., Chandran S. and Madabhushi A. (2009).

CLASSIFYING AYURVEDIC PULSE SIGNALS VIA CONSENSUS LOCALLY LINEAR EMBEDDING.

In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing, pages 388-395

DOI: 10.5220/0001554903880395

 SciTePress

nant women, more easily compared to conventional

allopathic techniques. Pulse based diagnosis also has

the advantage of being inexpensive, non-invasive,and

painless. The practitioners ‘feel’ for a certain pattern

in the pulse which forms the basis of their diagno-

sis. This technique requires a high degree of exper-

tise. The paucity of expert Ayurvedic practitioners

has limited the more widespread use and popularity

of the Ayurvedic technique.

The goal of this work is to develop a computer

aided diagnosis (CAD) system for the automated, re-

producible analysis of Ayurvedic pulse signals. To

the best of our knowledge, this work represents the

ﬁrst attempt at CAD of Ayurvedic pulse signals.

Since the Ayurvedic pulse signal is a time series,

pattern recognition methods that have been previously

applied to analysis of other time series data (ECG,

EMG) might seem appropriate for CAD of PBD.

Pattern recognition in electrocardiogram (ECG) has

been applied to QRS/PVC recognition and classiﬁca-

tion, the recognition of ischemic beats and episodes,

and the detection of atrial ﬁbrillation using nonlin-

ear transformations and neural networks (Maglav-

eras et al., 1998). In (Maglaveras et al., 1998), a

model-based approach for classiﬁcation of ECG stud-

ies based on previously deﬁned signatures of normal

and diseased ECG signals was employed. Given that

this is a ﬁrst CAD attempt at Ayurvedic PBD, quan-

titative signatures for normal and diseased patterns

haveyet to be studied and modelled. We consequently

explore a domain independent scheme for classiﬁca-

tion of the pulse data via dimensionality reduction.

Dimensionality reduction (DR), is a transforma-

tion of the original high-dimensional feature space

to a space of eigenvectors which are capable of de-

scribing the data in far fewer dimensions. DR also

permits the visualization of individual data classes

and identiﬁcation of possible subclasses within the

high dimensional data. The most popular method for

DR is Principal Component Analysis (PCA) which

attempts to ﬁnd orthogonal eigenvectors accounting

for the greatest amount of variability in the data.

PCA assumes that the data is linear and the embed-

ded eigenvectors represent low-dimensional projec-

tions of linear relationships between data points in

high-dimensional space. However, our previous re-

search has strongly suggested that biomedical data

is highly nonlinear in nature (Lee et al., 2008) and

that nonlinear DR schemes such as Isometric Map-

ping (Isomap) (Tenenbaum et al., 2000), Locally Lin-

ear Embedding (LLE), (Roweis and Saul, 2000) are

more appropriate for projection and subsequent clas-

siﬁcation of high-dimensional data including protein,

gene-expression, and spectroscopic data. LLE and

Isomap assume that the high dimensional data on a

high-order curve that is highly nonlinear and hence

object distances measured on this nonlinear manifold

should be geodesic as opposed to Euclidean. Nonlin-

ear methods attempt to map data along this nonlinear

manifold by assuming only neighboring points (deter-

mined via geodesic proximity) to be similar enough to

be mapped linearly with minimal error. The nonlinear

manifold can then be reconstructed based on these lo-

cally linear assumptions.

NLDR schemes like LLE determine the neighbor-

ing locations on the manifold (via Euclidean distance)

and map the neighborhood associated with each ob-

ject into the reduced dimensional embedding space.

The size of the local neighborhood within which LLE

assumes local linearity is however determined by a

free parameter κ. Optimal estimation of κ is still an

open problem. In (Tiwari et al., 2008) a new NLDR

scheme, C-LLE, that is able to handle the limitations

of LLE by avoiding the κ estimation, focusing instead

on optimally determining pairwise object distances in

the low dimensional embeddingspace, was presented.

Another limitation of LLE is that it traditionally

employs the Euclidean distance measure to deter-

mine neighbors within local patches on the manifold.

While the Euclidean distance measure is appropriate

for measuring the distance between objects character-

ized by discrete attributes, it is less appropriate for

measuring pulse signal similarity. Non-Euclidean dis-

tance measures such as mutual information (MI), en-

tropy correlation coefﬁcient (ECC), and the relative

entropy (RE) have been shown to be more appropri-

ate for measuring the similarity between signals com-

pared to the L2 norm (Tononi et al., 1996). In this

paper, the C-LLE algorithm is employed in conjunc-

tion with such signal similarity measures as MI, ECC,

and RE to embed Ayurvedic pulse signals in a lower-

dimensional embedding space. Prior to embedding,

the pulse signals are ﬁrst aligned with respect to each

other so that the pulse peaks for the different studies

are in concordance. A consensus clustering (Strehl

and Ghosh, 2002) algorithm is then employed to dis-

criminate between the normal and diseased pulse sig-

nals in the lower dimensional embedding space. The

major contributions of this work are:

• To the best of our knowledge, this is the ﬁrst

CAD system for classiﬁcation and analysis of tra-

ditional Indian Ayurvedic pulse medicine.

• Our CAD approach employs the C-LLE algo-

rithm that we have previously shown to outper-

form LLE, Isomap.

• We introduce the use of non-Euclidean distance

measures (MI, ECC, RE) geared speciﬁcally

to determining signal similarity for identifying

CLASSIFYING AYURVEDIC PULSE SIGNALS VIA CONSENSUS LOCALLY LINEAR EMBEDDING

389

neighbors in the high dimensional space. Our hy-

pothesis is that the use of these distance measures

will result in a more meaningful, accurate low di-

mensional embedding for pulse signal data.

The remainder of the paper is organized as follows.

Section 2 gives a brief review of dimensionality re-

duction methods used and the motivation for C-LLE.

Section 3 provides an overview of the CAD system.

Section 4 describes our experimental design and gives

a detailed description of C-LLE. In Section 5 we

present the qualitative and quantitative results of our

CAD system and concluding remarks, future direc-

tions are presented in Section 6

2 CONSENSUS LOCALLY

LINEAR EMBEDDING (C-LLE)

2.1 Limitations of Nonlinear

Dimensionality Reduction (NLDR)

Methods

NLDR schemes such as LLE (Roweis and Saul,

2000) and Isomap (Tenenbaum et al., 2000) assume

that an object in high-dimensional space can be de-

scribed by linear relationships with its nearest neigh-

bors. Both LLE and Isomap attempt to map ob-

jects c, d ∈ S that are adjacent (via geodesic dis-

tance) in high-dimensional space to nearby points in

the low-dimensional embedding, P(c), P(d), where

P(c), P(d) represent the Eigenvectors associated with

c, d ∈ S. LLE attempts to solve this problem by

deﬁning a locally linear neighborhood for each c ∈ S,

the size of the neighborhood being determined by κ,

parameter controlling the size of the neighborhood

within which local linearity is assumed. LLE then at-

tempts to non-linearly project each c to P(c) so that

the κ neighborhood of c ∈ S is preserved. While

Roweis and Saul (Roweis and Saul, 2000) have sug-

gested that the lower dimensional embeddings are

greatly robust to κ values, our own experiments have

indicated otherwise (Lee et al., 2008). Note that,

Roweis and Saul’s experiments were performed on

dense, synthetic datasets that are very different from

highly noisy, nonlinear real world datasets considered

in this work. It is our contention that in general it is

not possible to ﬁnd a global κ value that optimally ﬁts

all parts of the high-dimensional data.

2.2 Motivation for Consensus Locally

Linear Embedding

One of the solutions to enable for LLE to work op-

timally and generally on real world data, κ needs to

be locally estimated in different regions in the data

space. While some researchers have recently begun

to explore approaches to locally and adaptively esti-

mate κ, (Tong and Zha, 2008) (Wang et al., 2004),

the C-LLE scheme aims to estimate the pair-wise ob-

ject adjacency

W(i, j) in the low dimensional em-

bedding between two objects c

, c

∈ S, where i, j ∈

{1, ··· , |S|}. We formulate the problem of estimating

object distances

W(i, j) as a Maximum Likelihood

Estimation problem (MLE) from multiple approxima-

tionsW

(i, j) obtained by varying κ. The spirit behind

C-LLE is that it combines multiple low dimensional

data representations obtained via LLE for different

κ values to provide a stable embedding representing

the true class relationship between objects in the high

dimensional space. Analogous to constructing Bag-

ging classiﬁer ensembles (Breiman, 1996), the idea

behind C-LLE is to combine multiple weak embed-

dings so that the strong ﬁnal embedding accurately re-

ﬂects low-dimensional relationships. In addition, C-

LLE allows for incorporation of non-Euclidean simi-

larity measures in the original pulse space. Our con-

tention is that these pulse signal similarity measures

are more appropriate compared to the L2 norm. In

(Tiwari et al., 2008), the utility of C-LLE in identi-

fying and classifying prostate cancer using the Mag-

netic Resonance Spectroscopic Imaging (MRSI) data

was demonstrated.

3 SYSTEM OVERVIEW

Our CAD system for Ayurvedic pulse signal classi-

ﬁcation (Figure 1) involves obtaining the Ayurvedic

pulse signals in digital form, after which they are

noise ﬁltered and baseline corrected. The pulse sig-

nals are aligned with respect to each other based on

their peaks. The aligned pulse data is embedded in a

lower dimensional sub-space via C-LLE. The signals,

in their reduced low-dimensional representation, are

then classiﬁed into distinct classes via consensus

k-means clustering (Strehl and Ghosh, 2002).

Data Description. The two cohorts of 24 and 26

Ayurvedic pulse signals acquired at different frequen-

cies are brieﬂy described in Table 1. The data was

collected by a pulse waveform acquiring device (Joshi

et al., 2007) that records the pressure felt by the sen-

sors at three different points. Although the device

BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing

390

Figure 1: Flow diagram showing the different components of our C-LLE based Ayurvedic pulse diagnosis CAD system.

records all three pulse waveforms, we have used only

the Vata pulse for the purposes of this investigation.

The true condition for each patient was determined

by an expert Ayurvedic pulse practitioner.

Table 1: Description of patient database.

Condition Frequency No. of samples

Normal 100 10

Slipped disk 100 8

Stomach ailment 100 6

Normal 500 4

Diabetes 500 7

Slipped disk 500 5

Headaches 500 3

Stomach ailments 500 7

4 EXPERIMENTAL DESIGN

4.1 Pre-processing

For each patient study c ∈ S, there is an associated

D-dimensional valued pulse vector F(c) = [ f

{1, ··· , D}] where f

sity recorded at every instant. We denote via ∆ =

{LLE, Isomap, C-LLE} the set of dimensionality re-

duction techniques considered in this paper. For each

study c and associated pulse vector F(c), initial pre-

processing involves the following:

1. Respiration and artifact motion during pulse

waveform acquisition can introduce baseline wan-

der, which can be removed via the adaptive base-

line wander removal method described in (Xu

et al., 2002).

2. Each time series F(c) is ﬁltered to remove high

frequency noise via a soft thresholding wavelet

scheme (Novak et al., 2000).

3. Each of the signals F(c), c ∈ S, is then centered on

the mean and normalized. Figure 2 shows a pulse

signal F(u) (a) prior to and (b) following noise

and baseline correction and pulse signal normal-

ization.

(a) (b)

Figure 2: The pulse signal (a) prior to and (b) following

noise and baseline correction and pulse signal normaliza-

tion.

4.2 Pulse Signal Alignment

Pulse signal alignment is a necessary prerequisite to

computing similarity between data points and identi-

fying neighbors in the high-dimensional pulse signal

space. For instance, if the Euclidean metric is em-

ployed to measure pulse signal similarity, an offset of

even a single time point can result in an incorrect dis-

tance value.

Each time-signal F(c) is characterized by a cer-

tain periodic pattern of peaks. A simple peak detec-

tion algorithm (Billauer, 2004) was used to ﬁnd the

dominant peaks in F(c), ∀c ∈ S. The ﬁrst occurrence

of a dominant peak in F(c) was identiﬁed on all c ∈ S

which were then aligned with respect to each other.

Note that while additional anchor points (additional

modes) could also have been used for the pulse signal

alignment, Figure 3(b) suggests that a single anchor

point (in this case the ﬁrst dominant peak) resulted

in reasonable alignment. The pulse signal alignment

method is analogous to an intensity standardization

scheme that we previously presented (Madabhushi

and Udupa, 2005) to correct for nonlinear intensity

artifacts in MRI. Figure 3 shows the different signals

(a) prior to and (b) following alignment.

4.3 Similarity Measures

LLE, Isomap identify object neighbors as those that

are in proximity of each other in terms of the Eu-

clidean distance metric. The L2 norm is not however

optimally suited for measuring pulse signal similar-

ity. Consequently we consider several non-Euclidean

metrics (described in sections 4.3.1 - 4.3.4) that are

more appropriate for measuring signal similarity.

CLASSIFYING AYURVEDIC PULSE SIGNALS VIA CONSENSUS LOCALLY LINEAR EMBEDDING

391

(a) (b)

Figure 3: Five pulse signals superimposed (a) before and

(b) after pulse signal alignment. Notice that the signals are

more aligned.

4.3.1 Euclidean Distance

Consider the two pulse signal vectors F(c) and F(d)

for c, d ∈ S. The Euclidean distance between them is

deﬁned as

(c, d) =

∑

( f

(d))

(1)

where t ∈ {1, ..., D}. The Euclidean distance met-

ric requires the existence of an orthogonal coordi-

nate system. Since the individual components of F(c)

(c), t ∈ {1, ··· , D}) do not constitute an orthogo-

nal basis, Euclidean distance is perhaps a sub-optimal

measure for determining signal similarity.

4.3.2 Normalized Mutual Information

In information theory, the Shannon entropy or infor-

mation entropy is a measure of the uncertainty asso-

ciated with a random variable. The vector of values

F(c), associated with a signal takes can be thought

of as a random variable. From a signal we can de-

rive the probability distribution of these values. These

probability distributions p(x

) are used to deﬁne the

information entropy of a discrete random variable

X = {x

, ··· , x

} as,

H(X) = −

∑

i=1

p(x

)log p(x

) (2)

Considering two random variables X and Y, their joint

entropy is deﬁned to be

H(X, Y) = −

∑

x,y

log p

x,y

(3)

where p

x,y

is the probability density function for the

joint distribution of X and Y. The mutual information

(MI) between these two random variables is deﬁned

to be

I(X, Y) = H(X) + H(Y) − H(X, Y) (4)

MI measures the dependence of one variable on the

other which is a similarity measure, is used widely

in medical image registration (Pluim et al., 2003). A

normalized variant of MI is deﬁned as follows (Pluim

et al., 2003).

NMI(X, Y) =

H(X) + H(Y)

H(X, Y)

(5)

When the two variables X and Y are completely iden-

tical, NMI(X, Y) = 2. Thus, we deﬁne the distance

metric Γ

NMI

= 2− NMI.

4.3.3 Entropy Correlation Coefﬁcient (ECC)

Another measure which can be directly calculated

from the entropy values is the Entropy Correlation

Coefﬁcient (ECC) and is deﬁned as follows (Pluim

et al., 2003):

ECC(X, Y) = 2−

2H(X, Y)

(H(X) + H(Y))

(6)

Therefore, ECC = 1 if the two distributions are iden-

tical and ECC = 0 if they are completely indepen-

dent. This allows us to deﬁne the distance metric

ECC

= 1− ECC.

4.3.4 Relative Entropy

Relative Entropy (RE), or the Kullback-Leibler Dis-

tance (Cover and Thomas, 1991), used for measuring

the distance between probability distributions is de-

ﬁned as follows:

RE(X, Y) =

∑

p(x

)log

p(x

)

p(y

)

(7)

or in other words

RE(X, Y) = C(X, Y) − H(X) (8)

where C(X, Y) is deﬁned as the cross entropy of the

two variables. Note that while the Euclidean, MI, and

ECC measures are both symmetric and reﬂexive, the

RE measure is only reﬂexive.

4.4 Consensus Locally Linear

Embedding Framework

The spirit behind C-LLE is that it combines multiple

low-dimensional data representations obtained via

LLE for different κ values to provide a stable embed-

ding representing the true class relationship between

objects in the high dimensional space. Analogous to

constructing Bagging classiﬁer ensembles (Breiman,

1996), the idea behind C-LLE is to combine multiple

weak embeddings so that the strong ﬁnal embedding

accurately reﬂects low-dimensional relationships.

BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing

392

Step 1. Generating multiple lower dimen-

sional embeddings by varying the parameter κ:

We generate a set of multiple embeddings S

(c)

for c ∈ S, by varying the neighborhood parameter

κ ∈ {2, . . . , K} using LLE. The distance between

any two objects c

, c

∈ S and i, j ∈ {1, . . . , |S|} is a

function of κ. Thus ||S

) − S

)||

will vary as a

function of κ, where ψ is the distance measure.

Step 2. Obtain MLE of pairwise object adja-

cency:

A confusion matrix W

∈ ℜ

|S|×|S|

representing the

adjacency between any two time series c

, c

∈ S and

i, j ∈ {1, . . . , |S|} in the lower dimensional embedding

(i, j) = D

, c

) =



) − S

)



, (9)

where κ ∈ {2, ··· , K}. MLE of D

, c

) is estimated

as the mode of all adjacency values in

(i, j) over

all κ. This

D for all c ∈ S is then used to obtain the

new confusion matrix

Step 3. Multidimensional scaling (MDS):

We apply multidimensional scaling (Venna and

Kaski, 2006) (MDS) to

W to achieve the ﬁnal stable

embedding

S(c), for all c ∈ C. MDS is implemented

as a linear method that preserves the Euclidean

geometry between each pair of objects c

, c

∈ S, i,

j ∈ {1, ..., |S|}. This is done by ﬁnding optimal posi-

tions for the data points c

, c

in lower-dimensional

space through minimization of the least squares error

in the input pairwise Euclidean distances in

W. After

the application of LLE in Step:1, we have essentially

embedded the points in a linear subspace, where the

L2 norm is appropriate.

4.5 Consensus k-means Clustering on

the Embedding

Let Q be the set of all low dimensions we are rang-

ing over for embedding. The output of MDS is an

embedding location

S(c), ∀c ∈ S which spans Q ∈

{3, ··· , 15}. This set can be represented by a |S| × q

matrix where each row is an embedding in q dimen-

sional space of the original point in q dimensions

where q ∈ Q. The next step on acquiring the embed-

ding in lower dimensions is to group all c ∈ S points

into two clusters (normal and abnormal). For the

ﬁrst cohort consisting of 100Hz data, we are group-

ing the points into normal and abnormal cluster. This

grouping is done using consensus k-means clustering

algorithm (Strehl and Ghosh, 2002). To overcome

the instability associated with centroid based cluster-

ing algorithms like k-means clustering, we generate

multiple weak clusterings V

, V

, a ∈ {1, . . . A} by

repeated application of k-means clustering on

S(c),

∀c ∈ S, a total of A times. Each cluster is a set of ob-

jects assigned the same label V

, V

, by the k-means

algorithm. As the number of objects in a cluster keep

on changing, we calculate a co-association matrix H

with the assumption that points belonging to a natu-

ral cluster are very likely to be co-located in the same

cluster for each iteration a. Co-occurrences of pairs

of points c

, c

∈ S are taken as votes for their asso-

ciation. H(i, j) thus is the number of times c

and c

were found in the same cluster over A iterations. If

H(i, j) = A, it is highly likely that c

and c

belong to

the same cluster. MDS to H followed by a ﬁnal un-

supervised classiﬁcation using k-means clustering is

used to obtain the ﬁnal stable clusters

and

5 RESULTS

5.1 Qualitative Results

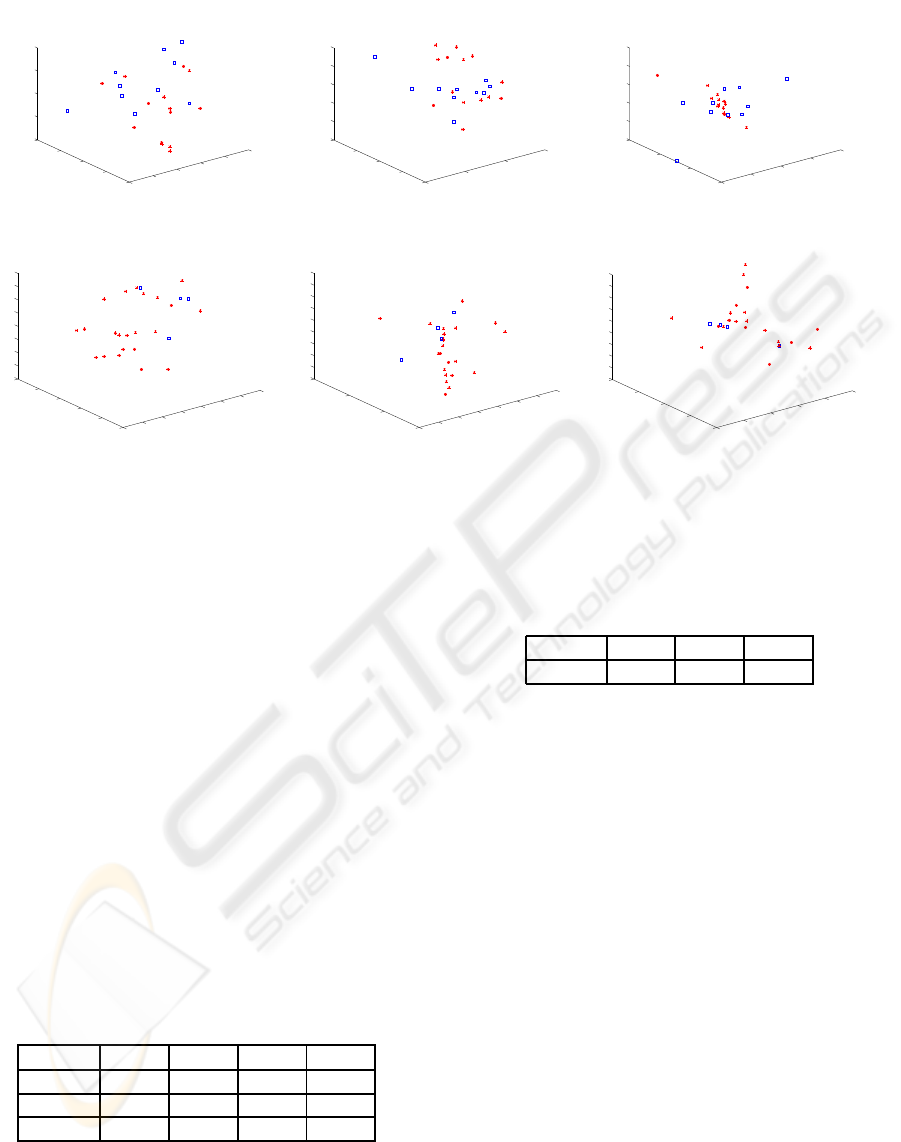
Figure 4 (a) (d) show the low-dimensional embedding

representation of the 100Hz and 500Hz data respec-

tively obtained via C-LLE. Figures 4 (b) (c) show the

corresponding embedding results obtained with LLE

and PCA for the 100Hz cohort and ﬁgures 4 (e) (f)

for LLE and Isomap embeddings the 500Hz data. In

each case, the blue squares represent the normal stud-

ies and red stars represent diseased cases. The embed-

ding results in Figures 4(a)-(c) were all obtained by

projecting the aligned pulse data into 3 dimensions

via the relative entropy similarity measure. In com-

paring Figures 4(a)-(c), and Figures 4 (d)-(f) it is ap-

parent that the greatest separation between the normal

and diseased studies is obtained via C-LLE. LLE per-

forms marginally better compared to PCA in terms of

separating the pulse signals, reinforcing further that

NLDR schemes outperform linear DR schemes for

biomedical data.

5.2 Quantitative Results

In order to quantitatively evaluate the different ap-

proaches, the following experiments were performed:

(a) C-LLE was compared against other NLDR meth-

ods (LLE, Isomap) in terms of classiﬁcation accuracy

and for different similarity measures (b) the effect of

pulse signal alignment of the data on the results of

NLDR was analyzed for the 100Hz signal. For the

500Hz signal we compare the performance of C-LLE

over different similarity measures.

CLASSIFYING AYURVEDIC PULSE SIGNALS VIA CONSENSUS LOCALLY LINEAR EMBEDDING

393

−0.3

−0.2

−0.1

0.1

0.2

−0.4

−0.2

0.2

0.4

−0.2

−0.1

0.1

0.2

−1

−0.5

0.5

−0.4

−0.2

0.2

0.4

−0.6

−0.4

−0.2

0.2

0.4

−5

x 10

−5

x 10

−6

−4

−2

x 10

(a) (b) (c)

−0.4

−0.3

−0.2

−0.1

0.1

0.2

0.3

−0.6

−0.4

−0.2

0.2

0.4

−0.4

−0.3

−0.2

−0.1

0.1

0.2

0.3

0.4

−0.6

−0.4

−0.2

0.2

0.4

0.6

0.8

−0.5

0.5

−0.4

−0.3

−0.2

−0.1

0.1

0.2

0.3

0.4

0.5

−0.6

−0.4

−0.2

0.2

0.4

−0.2

−0.1

0.1

0.2

−0.25

−0.2

−0.15

−0.1

−0.05

0.05

0.1

0.15

0.2

(d) (e) (f)

Figure 4: Low-dimensional embedding of 100Hz pulse data obtained via (a) C-LLE, (b) LLE, and (c) PCA after alignment,

and the same for 500Hz data using (d) C-LLE, (e) LLE (f) Isomap. The red asterisks represent diseased pulse samples whereas

the blue squares represent normal.

5.2.1 Comparison of C-LLE with other DR

Methods for Different Similarity Measures

We compare the classiﬁcation accuracy as obtained

by C-LLE with LLE and Isomap over the 4 simi-

larity measures Γ

, Γ

NMI

, Γ

ECC

and Γ

. Table 2

clearly indicates that C-LLE achieves a higher classi-

ﬁcation accuracy than LLE and Isomap for all 4 simi-

larity measures for the 100Hz cohort normal vs abnor-

mal classiﬁcation. C-LLE with Γ

as the similarity

measure yields a classiﬁcation accuracy of 80.57%,

signiﬁcantly higher compared to LLE and Isomap.

With the exception of Γ

, all C-LLE results are over

70%. The classiﬁcation accuracy for Γ

is the lowest

among all similarity measures for all the 3 methods.

Table 2: Classiﬁcation accuracy in (%) of DR methods for

100Hz data for normal vs abnormal classiﬁcation after pulse

alignment.

∆|Γ Γ

NMI

ECC

C-LLE 80.57 72.20 70.83 60.08

LLE 64.16 60.83 61.67 41.66

Isomap 46.36 21.00 58.82 48.67

For the 500Hz signal, we obtained the follow-

ing results for C-LLE across 3 similarity measures.

We observe that Γ

provides the highest accuracy of

classiﬁcation of 88.34%.

Table 3: Classiﬁcation accuracy (in %) of C-LLE for 500Hz

data for normal vs abnormal classiﬁcation.

∆|Γ Γ

NMI

C-LLE 88.34 71.15 76.92

5.2.2 Effect of Pulse Signal Alignment on

Classiﬁcation Accuracy of C-LLE and

LLE over 4 Different Similarity Measures

Table 4 lists the classiﬁcation accuracy obtained via

C-LLE and LLE over different similarity measures

with and without pulse signal alignment for the

100Hz data set for normal vs abnormal classiﬁcation.

The columns ‘w’ indicate with alignment, ‘w/o’ is

without alignment. As the results in Table 4 clearly

reveal, the classiﬁcation accuracy results obtained fol-

lowing pulse signal alignment are consistently higher

compared to the results obtained without pulse sig-

nal alignment, independent of the NLDR method and

similarity measure employed.

6 CONCLUDING REMARKS AND

FUTURE WORK

In this paper we have presented a novel nonlinear di-

mensionality reduction technique (Consensus Locally

BIOSIGNALS 2009 - International Conference on Bio-inspired Systems and Signal Processing

394

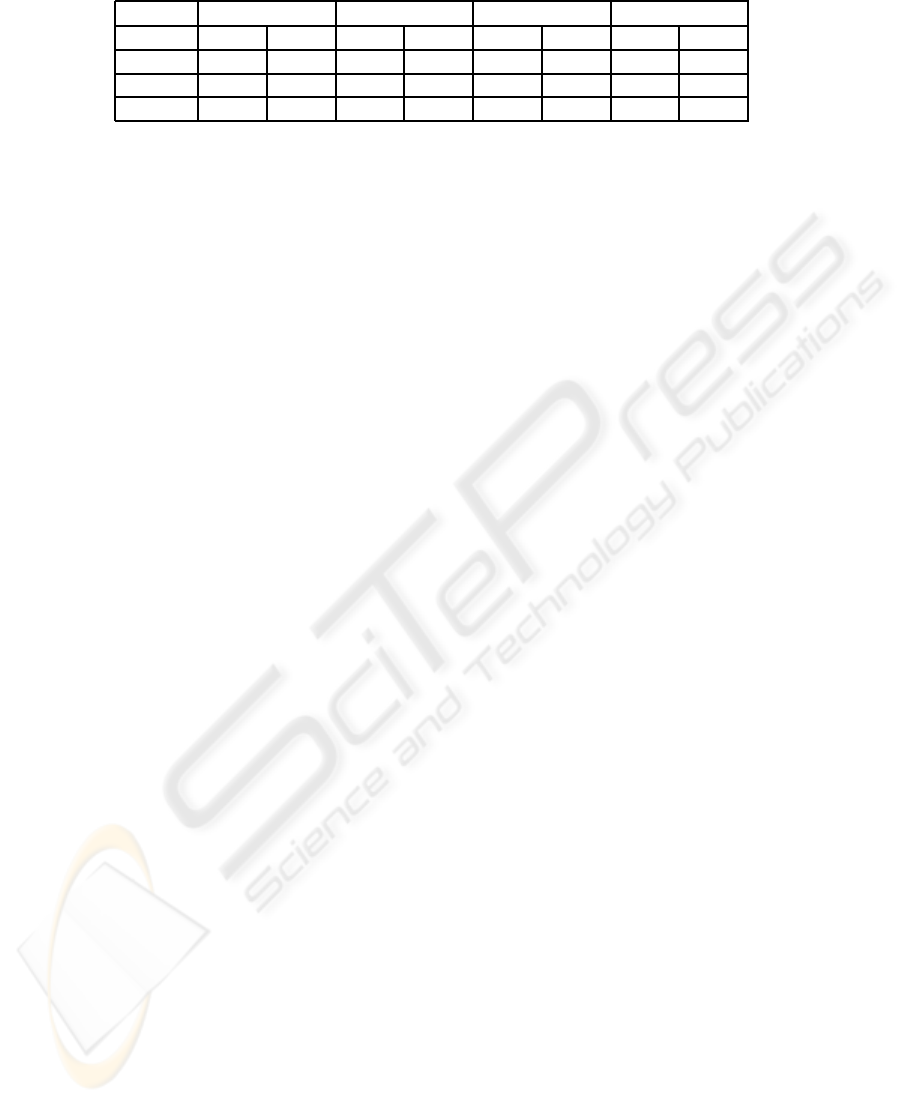
Table 4: Effect of Pulse Signal Alignment on the Classiﬁcation Accuracy (in %) for the 100Hz data.

∆|Γ Γ

NMI

ECC

– w w/o w w/o w w/o w w/o

C-LLE 60.08 50.59 72.20 32.74 80.57 32.73 70.83 50.00

LLE 41.66 54.50 60.83 55.35 64.16 52.38 61.67 52.97

Isomap 55.35 61.16 21.00 52.97 46.36 31.67 58.82 32.91

Linear Embedding) for the classiﬁcation and analy-

sis of Ayurvedic pulse signals. To the best of our

knowledge, this is the ﬁrst CAD system for analysis

of traditional Ayurvedic pulse signals. Another im-

portant contribution of the paper is the use of non-

Euclidean similarity measures that are more appro-

priate for measuring pulse signal similarity. These

measures (Mutual Information, Relative Entropy, and

Entropy Correlation Coefﬁcient) were all found to

consistently result in better classiﬁcation compared

to the L2 norm, independent of the NLDR method

used. Additionally, C-LLE consistently outperformed

LLE and Isomap for all 4 similarity measures consid-

ered. C-LLE with relative entropy as a distance mea-

sure provided a maximum accuracy of 80.57% for the

100Hz data, and a maximum of 88.34% for the 500Hz

data. In future work, we will explore in greater detail

the pulse signals that were misclassiﬁed by our CAD

scheme. We will also explore alternative representa-

tions of the data such as independent components and

H¨older exponents for feature selection. Finally, we

will be looking to evaluate our methods on a larger

data cohort.

REFERENCES

Billauer, E. (2004). peakdet: Peak detection using matlab.

Breiman, L. (1996). Bagging predictors. Machine Learn-

ing, 24(2):123–140.

Cover, T. M. and Thomas, J. A. (1991). Elements of Infor-

mation Theory. John Wiley & Sons, Inc.

Joshi, A., Kulkarni, A., Chandran, S., Jayaraman, V. K., and

Kulkarni, B. D. (2007). Nadi tarangini: A pulse based

diagnostic system. In IEEE Engineering in Medicine

and Biology Society, pages 2207–2210.

Lad, V. (2005). Secrets of the the pulse: The ancient art of

ayurvedic pulse diagnosis. Motilal Banarasidass.

Lee, G., Rodriguez, C., and Madabhushi, A. (2008). Investi-

gating the efﬁcacy of nonlinear dimensionality reduc-

tion schemes in classifying gene and protein expres-

sion studies. IEEE/ACM Transactions on Computa-

tional Biology and Bioinformatics, 5(3):368–384.

Madabhushi, A. and Udupa, J. (2005). Evaluating inten-

sity standardization and inhomogeneity correction in

magnetic resonance images. IEEE Transactions on of

Medical Imaging, 24(5):561–576.

Maglaveras, N., Stamkopoulos, Diamantaras, T., C., P., and

Strintzis, M. (1998). Ecg pattern recognition and clas-

siﬁcation using non-linear transformations and neural

networks: A review. International Journal of Medical

Informatics, 52(1-3):191–208.

Novak, D., Eck, C., Perez-Cortes, J. V., and Andreu-Garcia,

G. (2000). Denoising electrocardiographic signals us-

ing adaptive wavelets. In BIOSIGNAL.

Pluim, J., Maintz, P. W., and Viergever, M. (2003). Mutual-

information-based registration of medical images: A

survey. IEEE Transactions on Medical Imaging.

Roweis, S. and Saul, L. (2000). Nonlinear dimensionality

reduction by locally linear embedding. Science, v.290,

pages 2323–2326.

Strehl, A. and Ghosh, J. (2002). Cluster ensembles – a

knowledge reuse framework for combining multiple

partitions. Journal on Machine Learning Research

(JMLR), 3:583–617.

Tenenbaum, J. B., de Silva, V., and Langford, J. C. (2000).

A global geometric framework for nonlinear dimen-

sionality reduction. Science.

Tiwari, P., Rosen, M., and Madabhushi, A. (2008). In MIC-

CAI, volume 5242, pages 330–338.

Tong, L. and Zha, H. (2008). Riemannian manifold learn-

ing. IEEE Transactions on Pattern Analysis and Ma-

chine Intelligence, 30:796–809.

Tononi, G., Sporns, O., and Edelman, G. M. (1996). A

complexity measure for selective matching of signals

by the brain. PNAS, 93(8):3422–3427.

Venna, J. and Kaski, S. (2006). Local multidimensional

scaling. Neural Networks, 19:889–899.

Wang, J., Zhang, Z., and Zha, H. (2004). Adaptive manifold

learning. NIPS.

Xu, L., Zhang, D., and Kuanquan, W. (2002). Adaptive

baseline wander removal in the pulse waveform. pages

143–148.

CLASSIFYING AYURVEDIC PULSE SIGNALS VIA CONSENSUS LOCALLY LINEAR EMBEDDING

395