
NEW ALGORITHMS FOR GPU STREAM COMPACTION
A Comparative Study
Pedro Miguel Moreira
1,2
, Luís Paulo Reis
2,3
and A. Augusto de Sousa
2,4
1
ESTG-IPVC, Instituto Politécnico de Viana do Castelo, Viana do Castelo, Portugal
2
DEI/FEUP, Faculdade de Engenharia da Universidade do Porto, Porto, Portugal
3
LIACC, Laboratório de Inteligência Artificial e Ciência de Computadores, Porto,Portugal
4
INESC-Porto, Instituto de Engenharia de Sistemas e Computadores do Porto, Portugal
Keywords:
Stream Compaction, Parallel Algorithms, Parallel Processing, Graphics Hardware.
Abstract:
With the advent of GPU programmability, many applications have transferred computational intensive tasks
into it. Some of them compute intermediate data comprised by a mixture of relevant and irrelevant elements in
respect to further processing tasks. Hence, the ability to discard irrelevant data and preserve the relevant por-
tion is a desired feature, with benefits on further computational effort, memory and communication bandwidth.
Parallel stream compaction is an operation that, given a discriminator, is able to output the valid elements dis-
carding the rest. In this paper we contribute two original algorithms for parallel stream compaction on the
GPU. We tested and compared our proposals with state-of-art algorithms against different data-sets. Results
demonstrate that our proposals can outperform prior algorithms. Result analysis also demonstrate that there is
not a best algorithm for all data distributions and that such optimal setting is difficult to be achieved without
prior knowledge of the data characteristics.
1 INTRODUCTION
Graphics Processing Units (GPUs) are parallel plat-
forms which provide high computational power with
very large memory bandwidth at low cost. With the
advent of GPU’s programmability, many algorithms,
that usually were performed by the CPU, were en-
abled to run at the GPU side taking advantage from
its parallel processing capabilities. Nowadays, GPUs
are compelling programmable platforms, not only un-
der the graphics domain, but also for general pur-
pose computational intensive tasks, leading to a rel-
atively new research area focused on mapping gen-
eral purpose computation to graphics processing units
- GPGPU (Owens et al., 2007; GPGPU, 2008).
Stream compaction, also designated as stream
non-uniform reduction and also as stream filtering,
takes a data stream as input, uses a discriminator to se-
lect a wanted subset of elements, and outputs a com-
pacted stream of the selected elements, discarding the
rest.
Several computer graphics applications, making
use of the GPU programmable architecture, may
take advantage from parallel stream compaction al-
gorithms in several ways. Key benefits, enabled
by exclusion of non-relevant data, comprise: sav-
ings on computational effort on further processing
stages; better memory footprint; and savings on band-
width when data has to be readback to the CPU.
Stream compaction is also a fundamental compo-
nent on algorithms that deal with data partitioning
(e.g. some sorting algorithms and space hierarchies).
Reported work taking advantage from GPU stream
compaction include: collision detection (Horn, 2005;
Greß et al., 2006), ray-tracing (Roger et al., 2007),
shadow mapping (Lefohn et al., 2007), point list gen-
eration (Ziegler et al., 2006), and, in general, algo-
rithms that make use of data partitioning.
The current OpenGL specification (OpenGL
v.2.1) (Segal and Akeley, 2006) exposes two GPU
programmable units: the vertex and the fragment pro-
cessors. A third programmable unit, the geometry
processor, was recently exposed through OpenGL ex-
tensions (OpenGL Architecture Review Board, 2008)
but it has limited support and availability only on very
recent GPUs. Current GPUs are designed with several
vertex and fragment processor units enabling them
with high levels of parallelism.
The vertex processor has scatter capabilities (in-
direct writing) and also gather capabilities (indirect
reading) with the latter with some lack of support and
performance issues. The fragment processor has only
gather capabilities, through texture fetching.
More recently, the so-called Unified Architec-
119
Moreira P., Reis L. and de Sousa A. (2009).
NEW ALGORITHMS FOR GPU STREAM COMPACTION - A Comparative Study.
In Proceedings of the Fourth International Conference on Computer Graphics Theory and Applications, pages 119-128
DOI: 10.5220/0001783601190128
Copyright
c
SciTePress

tures (UA), were made available. The UA paradigm
comprises indistinct processors and features such as
global load-store memory, shared memory , and syn-
chronization mechanisms. However, these features
have restricted support as they are not currently ex-
posed to programmers but by proprietary APIs.
This paper presents original work on paral-
lel stream compaction algorithms for programmable
GPUs and compares them to state-of-the-art algo-
rithms. The algorithms are intended to be imple-
mented using widely supported features, such as
the exposed by OpenGL (Segal and Akeley, 2006;
Kessenich, 2006). We assume that the GPU has pro-
grammable vertex processors with scatter and (poten-
tially limited) gather abilities and programmable frag-
ment processors with gather abilities but without scat-
ter.
The rest of the paper is organized as follows. The
next section reviews relevant prior work on scan prim-
itives and stream compaction. Following (Section
3) introduces the original algorithms alongside with
a more detailed description of the tested algorithms.
The implementation and experimental setup are de-
scribed alongside with the achieved results in Section
4. At last, Section 5, outlines our major conclusions
alongside with possible directions to future work.
2 RELATED WORK
Stream compaction is an operator that takes a data
stream as input, uses a discriminator to select a valid
subset of elements, and outputs a compacted stream of
the selected elements, discarding the rest. Sequential
stream compaction is trivially implemented in O(s)
with a single pass over the data.
While seeming an inherently sequential com-
putation, stream compaction can be parallelized
using the all-prefix-sum (aka scan). The all-
-prefix-sum operation (Blelloch, 1990) takes a bi-
nary associative operator ⊕ and an ordered set
of elements with size s (e.g. an array or
stream): [a
0
,a
1
,...,a
s−1
]; and returns an ordered set:
[a
0
,(a
0
⊕ a
1
),...,(a
0
⊕ a
1
⊕ ... ⊕ a
s−1
)].
The parallel prefix-sum can be computed using a
recursive doubling algorithm, as described by Hillis
& Steele (Hillis and Steele JR, 1986) and used by
Horn (Horn, 2005) in a GPU implementation. The
recursive doubling has a total work of O(s · log(s)).
Hensley et al. (Hensley et al., 2005) also used the
recursive doubling algorithm to devise fast GPU gen-
eration of Summed Area Tables (Crow, 1984) which
can be thought as a 2D prefix-sum.
Sengupta et al. (Sengupta et al., 2006) imple-
mented a prefix-sum based on a balanced tree ap-
proach, as described by Blelloch (Blelloch, 1990),
with a computational complexity of O(s). They
also proposed a GPU work-efficient algorithm that
switches between the recursive doubling and balanced
tree based algorithms, in order to optimize the work
amongst the available parallel processors. More re-
cently, their approach was improved (Harris et al.,
2007) by making use of an optimized segmented
prefix-sum approach targeted to the new NVIDIA
CUDA API (Nickolls et al., 2008). By the same time,
Greß et. al (Greß et al., 2006) also devised a GPU im-
plementation with O(s) running time targeted to 2D
data and making use of a quadtree data structure.
The fundamental idea to achieve parallel com-
paction using the all-prefix-sum is to discriminate the
data using a value of one to mark invalid elements
and zero to mark valid elements. Then, the algorithm
proceeds by computing the all-prefix-sum of the dis-
criminated data. The resulting stream stores, for each
position, the number of invalid elements to the left.
This value corresponds to the displacement to the left
that each valid element has to undertake in order to
build the compacted stream (see Figure 1).
04623 5 71 8121410 11 13 159
original data
discriminated data
all-prefix-sum
compacted data
0 0 db 0 c 0a 0 0 0e 0 f 00
1 1 00 1 0 10 1 1 10 1 0 11
1 3 31 2 3 41 5 8 96 7 8 106
a e dc d f 0b 0 0 0e 0 f 00
04623 5 71 8121410 11 13 159
04623 5 71 8121410 11 13 159
04623 5 71 8121410 11 13 159
Figure 1: Parallel stream compaction based on the all-
prefix-sum.
If scatter capabilities are available, the compaction
process can be implemented in a single pass . As scat-
ter is not widely available at the fragment processing
level, it has to be converted into gather. Horn (Horn,
2005) devised a binary search mechanism in order to
enable stream compaction under such circumstances.
Roger et. al (Roger et al., 2007) described a hi-
erarchical stream compaction strategy that splits the
data into regular blocks, compacts them and finally
concatenates the compacted substreams. A higher
level prefix-sum is used to compute the displacements
of each compacted block. They suggest making use
of the scatter abilities of the geometry processors (or
alternatively the vertex processor), to avoid a block-
level gather-search and, therefore, enabling savings
on the total parallel work.
Ziegler et al. (Ziegler et al., 2006) introduced the
Histo-Pyramids algorithm, devoted to 2D data which,
which similarly to the work of Greßet al. (Greß et al.,
2006), uses a quadtree to encode the valid elements
GRAPP 2009 - International Conference on Computer Graphics Theory and Applications
120

and then extracts them into a compacted stream (actu-
ally a 2D texture) by means of a guided tree traversal
. This approach avoids the explicit computation of the
all-prefix-sum for all elements. . Though not chang-
ing the asymptotical complexity of prior algorithms,
the algorithm effectively reduces the total work, as
there are, in parallel, a number of tree traversals that
equals the number of valid elements.
In the following section we will introduce a new
algorithm (Section 3.3), the Run-Lengths of Zeros
(RLZ), that operates on an alternative domain than the
all-prefix-sum. We also describe the Binary-Tree al-
gorithm (Section 3.4) supported on ideas originally
described by Greß (Greß et al., 2006) and Ziegler
(Ziegler et al., 2006).
We tested these algorithms together with the
Jumping Jack algorithm (Section 3.2) devised by
(Moreira et al., 2009) and with (Horn, 2005) gather-
search algorithm (Section 3.1). In order to effi-
ciently handling large data streams, we adopted a
block based compaction framework, as introduced by
(Roger et al., 2007), and described in (Moreira et al.,
2009). For the parallel all-prefix-sum, we have imple-
mented the recursive doubling all-prefix-sum ((Hillis
and Steele JR, 1986), (Horn, 2005)) and the bal-
anced tree approach ((Blelloch, 1990; Sengupta et al.,
2006)).
3 ALGORITHMS
This section introduces original work and also de-
scribes current state-of-the-art algorithms for stream
compaction.
3.1 Gather-Search (Horn, 2005)
Daniel Horn (Horn, 2005) introduced a compaction
algorithm based on a binary-search procedure allow-
ing conversion of scatter into gather. Horn observed
that the all-prefix-sum is an ascending stream and
therefore a parallel search can be conducted in or-
der to find the data elements that have to displace to
each position in order to create the compacted stream.
The original algorithm computes the all-prefix-sum
based on the recursive doubling algorithm proposed
by Hillis & Steele (Hillis and Steele JR, 1986), but
any other method can be used.
Given a stream data[ ] with size s, and its cor-
responding all-prefix-sum pSum[ ] of invalid ele-
ments, with a total number of z invalid elements
(z = pSum[s − 1]) and v = s − z valid elements, a bi-
nary search is conducted in parallel for all output po-
sitions c ∈ [0, v[. The search goal is to find a valid
element displaced d positions to the right from the
current position c, such as pSum[c + d] = d (refer to
1). The possible displacements can take values on
the range d ∈ [0,z]. The binary search proceeds un-
til d = pSum[c + d] is satisfied and data[c + d] is a
valid element. The search solution has a computa-
tional complexity of order O(log(s)) and total work
of order O(s · log(s)).
3.2 Jumping-Jack(Moreira et al., 2009)
Jumping Jack was recently introduced by Moreira et
al. (Moreira et al., 2009) as a non-monotonic com-
paction algorithm. Non-monotonic compaction does
not preserve the relative order of the original data at
the output. Monotonicity is not a requirement for
many applications.
The algorithm is very simple to implement, and
is specially devoted to not very sparse data sets. For
very sparse streams the algorithm has a drop in perfor-
mance due to its imbalanced behavior. Therefore, in
order to handle large amounts of data, and to bound
the effect of the potential load imbalance, the algo-
rithm is proposed to operate over small-sized streams,
under a hierarchical compaction scheme (e.g. as in-
troduced by (Roger et al., 2007)).
For a stream with size s with v valid elements,
the main idea is to keep unchanged all the valid el-
ements positioned within the first v indexes, and fill
the other positions, originally occupied by invalid el-
ements, by finding the remaining valid elements. This
can be achieved by conducting a search on the named
MAS (maximum-allowable-size stream) which can
be computed straightforwardly from the all-prefix-
sum as MAS[i] = s− pSum[i]. The search is conducted
using the MAS as pointer stream and recurrently in-
spect the data at the pointed position until a valid ele-
ment is found. . The algorithm has a total linear work
of O(s) and the total work is bounded by O(s − v).
3.3 Run-Lengths of Zeros - RLZ
The design of the herein presented algorithm was
based on the observation that in the algorithm pro-
posed by (Horn, 2005) (Section 3.1), and when in
presence of large runs of invalid elements, the dis-
placement criterion is valid for the desired valid ele-
ment and for all the subsequent sequence of invalids.
Notice that the valid element is always positioned just
before (to the left) the sequence of invalid elements.
In such situation, the binary search process has often
to iterate (to lower indexes) until the desired element
is found.
NEW ALGORITHMS FOR GPU STREAM COMPACTION - A Comparative Study
121

The main idea was to use an alternative search do-
main, than the regular all-prefix-sum of invalid ele-
ments, that better captures the structure of the data.
We have designed the algorithm to operate on the all-
prefix-sum of the run-lengths (denoted from now as
pRLSum) of invalid sequences. This sequence is con-
structed by summing the lengths of the runs of invalid
elements. The run-lengths are positioned at the start
position of each run (from left to right). Figure 3 vi-
sually illustrates the concept, which will be detailed
in the next subsection. We will subsequently refer this
algorithm as Run-Lengths of Zeros, or RLZ for short.
The pRLSum stream has interesting properties
when compared to the regular all-prefix-sum stream.
The streams have value correspondence for valid el-
ements and the number of invalid elements can be
found at the last position. Distinctively, the pRLSum
only retains the interesting values, i.e. is composed by
the displacements values (until the last valid element).
We used these properties to devise a search to find
the desired displacements, in order to obtain a com-
pacted stream. We observed empirically that these
displacements can be quickly found using a recursive
forward search approach. Particularly, this forward
search is very quick for the first elements and for mod-
erate sized streams (e.g. in the order of hundreds or
thousands of elements).
The search is quite simple and proceeds as fol-
lows (Algorithm 1). For a given index i of the out-
put stream, one has to find the first displacement
such: displacement = prlSum[i + displacement].
Actually we observed that evaluating the condition
prlSum[i + displacement] = prlSum[i + prlSum[i +
displacement]] results more optimized and performs
about 20% faster.
Algorithm 1: Compaction using Run-Lengths
of Zeros.
begin
forall positions i ∈ [0, v[ in parallel do
curr ← prlSum [i]
next ← prlSum[i + curr]
while curr 6= next do
curr ← prlSum [i + next]
next ← prlSum[i + curr]
compact [i] ← data [i + curr]
end
Computing the pRLSum is costlier than comput-
ing the all-prefix-sum. Although, it is expected a
faster search process resulting in an overall perfor-
mance competitive with prior algorithms. It is also
expected that the algorithm performs better for data
with low frequency of change between valid and in-
valid elements, i.e. with medium to large sized runs
of valid / invalid elements.
1 3 31 3 3 61 6 8 106 8 8 106
04623571 8 12 1410 11 13 159
a e 1c d f 0b 0 0 01 0 1 00
1
1
1
1
1
3
8
8
3
3
3
6
3
6
66
33
0 0 db 0 c 0a 0 0 0e 0 f 00
[0+1] [1+1] [2+3] [3+3] [4+6] [5+8]
04623571 8 12 1410 11 13 159
pRLsum
data
compact
Figure 2: Graphical trace of the Run-Lengths of Zeros al-
gorithm.
3.3.1 Computing Run-Lengths
We devised a three stage parallel algorithm for com-
puting the all-prefix-sum of run-lengths. The overall
process is illustrated in Figure 3.
a 000 0 b c 0
0 111 1 0 0 1
0 122 1 0 0 3
0 002 0 0 0 3
0 552 2 2 2 5
original data
discriminated data
Stage 1 :RunLengthComputation
Stage 2 :Run‐Length Extraction
Stage 3 :All Prefix Sum
Figure 3: Computation of the all-prefix-sum of run-lengths,
pRLsum.
The first stage Run-Length Computation com-
putes, for each invalid element (marked as one), the
number of consecutive invalid records, to the right,
until a valid element is reached (or the end of the
stream). This value might be interpreted as the dis-
tance to the next valid element and the problem can be
thought as list-ranking within a list of lists. Positions
corresponding to valid elements store a zero. Notice
that the run-length of invalid elements is stored at the
leftmost position of the sequence.
For this stage, we developed a variation of the re-
cursive doubling algorithm to enable finding the run-
lengths. The algorithm is similar, except that it op-
erates in reverse direction and the addition is con-
ditioned by the value of the current position. The
explanation is as follows. A given position stores a
value corresponding to the number of consecutive el-
ements from its own position to offset positions to the
GRAPP 2009 - International Conference on Computer Graphics Theory and Applications
122
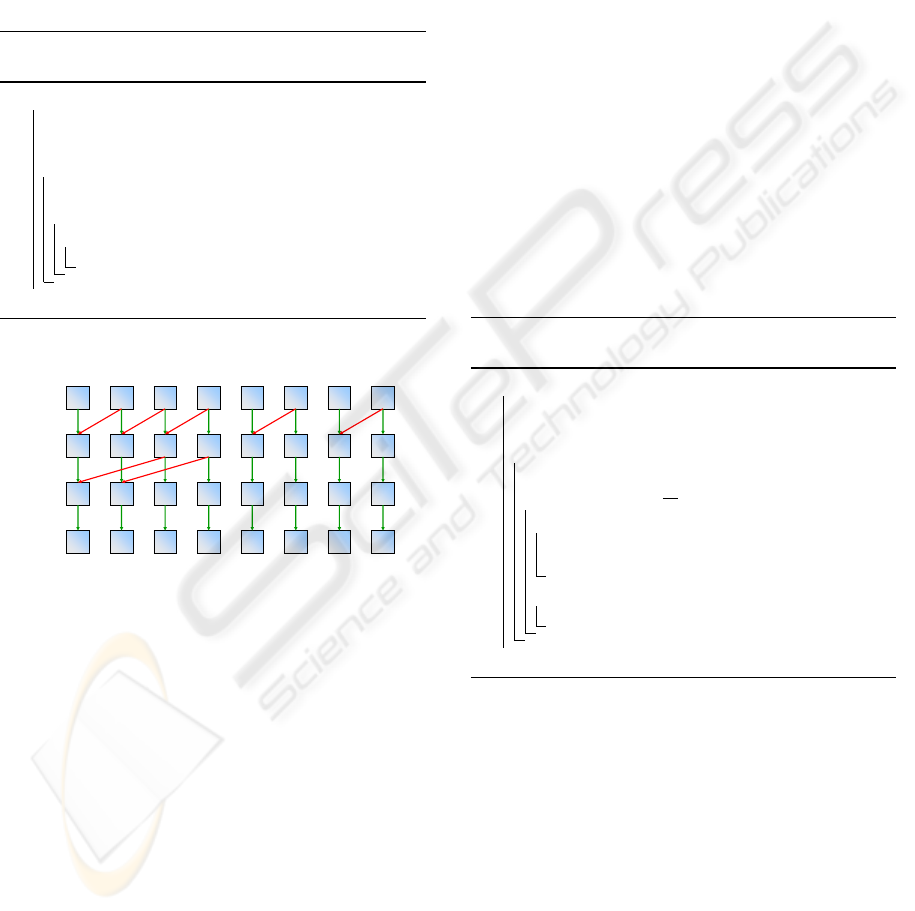
right. Accordingly, if this value is below the current
offset, the sequence is doubtlessly interrupted some-
where within that range. Hence, for each iteration,
the value stored offset positions away is added to the
current position, if and only if, the value in the cur-
rent position equals the offset. Pseudo-code for the
algorithm is given in Algorithm 2 and a visual trace
is illustrated by Figure 4. The algorithm has a paral-
lel computational complexity of O(log
2
(s)) with total
work of O(s · log
2
s).
Algorithm 2: Parallel run-length computation
(based on recursive doubling).
begin
output: RL[ ] : the output stream, initialized
with the discriminated data
for p ← 1tolog
2
(s) do
o f f set ← 2
p−1
forall i < s − o f f set in parallel do
if RL[i] = o f f set then
RL[i] ← RL[i] + RL[i + o f f set]
end
offset = 2
k
if a
k-1
[i] >= offset then
a
k
[i] = a
k-1
[i] + a
k-1
[i+offset]
else
a
k
[i] = a
k-1
[i]
1 111 1 0 1 0
2 122 1 0 1 0
3 122 1 0 1 0
3 122 1 0 1 0
original data
k=1,offset = 2
k=0,offset = 1
k=2,offset = 4
Figure 4: Illustration of the modified recursive doubling al-
gorithm to compute run-lengths of consecutive elements.
In order achieve the run-lengths computation with
a total work of order O(s), we have also developed
a variation to the all-prefix-sum algorithm proposed
by Blelloch (Blelloch, 1990). A visual illustration
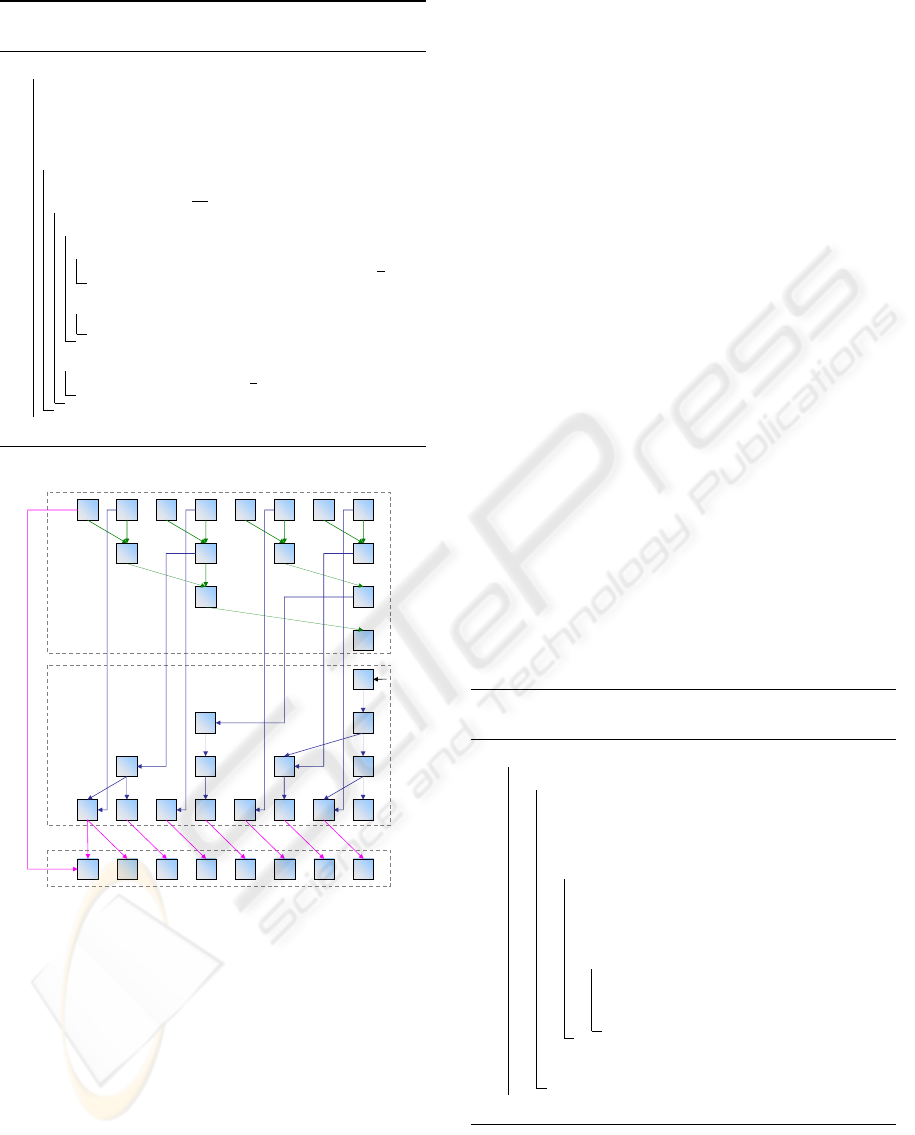
of the overall algorithm operation is depicted in Fig-
ure 5. The process comprises two fundamental steps.
The first, referred as the up-sweep (Algorithm 3), per-
forms as a conditioned binary reduction. For each
level, each node takes the value stored in its left child.
The value stored in its right child is added, if and only
if, the left child corresponds to a full node (i.e. all
leaves under it are ones). Therefore, each node will
store the length of the sequence (run of ones) start-
ing at the leftmost leaf of the corresponding subtree
(e.g. the root node stores the length of the run start-
ing at the first stream element). The second step,
referred as down-sweep (Algorithm 4), uses the val-
ues from the up-sweep to hierarchically build the run-
-lengths stream. The fundamental idea is to check if
the runs extend across subtrees and update the run-
lengths accordingly. The root node is initialized with
the identity value (zero). At each subsequent level,
each right child takes the value stored by its parent.
Each left child takes the value, computed in the up-
-sweep phase, of its right sibling. If the sibling node
corresponds to a full node, then it also adds the value
stored by its parent. A final adjustment step shifts the
values one position to the right and adds to the left-
most element the leftmost element of the original dis-
criminated stream, in order to obtain run-lengths at
the desired positions (possibly embedded in the last
level of the down-sweep). Notice that, as the given
pseudo-code assumes a start index of zero, right and
left child nodes correspond to odd and even indexes,
respectively. A GPU implementation, making use of
a double buffer (one to read and the other to write),
and switching the buffer roles after each pass, allows
to store alternate hierarchical levels of the up-sweep
and down-sweep at each buffer.
Algorithm 3: Up-Sweep stage of run-length
computation (based on balanced-tree).
begin
input : U S[0][ ] discriminated data
output: U S[ ][ ] all levels of the up-sweep
for p ← 1tolog
2
(s) do
o f f set ← 2
p−1
forall i from 0 to
s
2
p
− 1 in parallel do
if U S[p − 1][2i] = o f f set then
US[p][i] ←
US[p − 1][2i] +US[p − 1][2i + 1]
else
US[p][i] ← US[p − 1][2i]
end
The second stage comprises a fast (potentially
embedded in the previous or the next stage) filter-
ing stage designed to extract / filter the desired run-
lengths. As it can be observed, these elements are all
those that being non-null have a null element at his
left.
The third stage computes the desired all-prefix-
sum of the run lengths, e.g. using (Hillis and Steele
JR, 1986) or (Blelloch, 1990) or any other method.
Computing the pRLsum[ ] stream has the same
order of computational complexity as the all-prefix-
-sum, but it doubles the passes over the data, doing
nearly twice the work.
NEW ALGORITHMS FOR GPU STREAM COMPACTION - A Comparative Study
123
Algorithm 4: Down Sweep stage of run-length
computation (based on balanced tree).
begin
input : U S[ ][ ] all levels from the up-sweep
output: DS[0][ ] run-lengths
DS[log
2
(s)][0] ← 0
for p ← log
2
(s) − 1 downto 0 do
o f f set ← 2
p
forall i from 0 to
s
2
p
− 1 in parallel do
if isEven(i) then
if U S[p][i + 1] = o f f set then
DS[p][i] ← US[p][i + 1] + DS[p + 1][
i
2
]
else
DS[p][i] ← US[p][i + 1]
else
DS[p][i] ← DS[p + 1][
i
2
]
end
p=1
offset=1
p=2
offset=2
p=3
offset=4
p=2
offset=4
p=1
offset=2
p=0
offset=1
1 111 1 0 1 0
22 1 1
13
3
0
01
01 1 2
2 011 0 1 0 2
0
3 122 1 0 1 0
up-sweep
down-sweep
final adjustment
01234567
0123
01
0
0
01
0123
01234567
01234567
COREECTA
(corrigenda)
Figure 5: Illustration of the modified Blelloch’s (Blelloch,
1990) algorithm to enable computation of run lengths of
consecutive elements.
3.4 Binary-Tree
The design of the herein presented algorithm is
founded on ideas originally described by (Greß et al.,
2006) and by (Ziegler et al., 2006). The referred
works are mainly devoted to compaction of 2D data
(with potential extensions to 3D) and use a quadtree
as the fundamental data structure. Despite the similar-
ities, instead of a quadtree, our proposal uses a binary
tree as a fundamental data structure, and so, it can be
straightforwardly used to compact both linear and 2D
data. Furthermore, we propose the combination of its
operation with a block based compaction strategy.
The main idea behind the design of the algorithm
is to avoid the prior computation of the all-prefix-
sums. This can be achieved by encoding the data
stream into a binary tree where each node stores the
number of valid elements under it. Extraction of the
compacted stream is achieved by tree traversal.
The first step of the algorithm is to discriminate
the valid elements. In the following discussion it is
assumed that valid elements are flagged as true (ones)
and invalid elements are flagged as false (zeros).
The next step, binary tree encoding, comprises en-
coding the number of valid elements into a binary
tree. This is similar to a stream reduction operation
using addition as the reduction operator and preserv-
ing the intermediary results (i.e. preserving the over-
all reduction tree structure). At each level (pass), each
node computes the number of valid elements under
it, i.e. the sum of valid elements stored by its child
nodes. This process continues until the root level is
reached.
The root node stores the total number of valid el-
ements, i.e. the size of the compacted stream, v. This
binary reduction is achieved in log
2
(s) passes, being
s the size of the original stream. Notice that as for
each pass (tree level) the number of nodes is halved,
the total work has a linear order O(s), in respect to the
stream size .
Algorithm 5: Binary Tree Traversal (mono-
tonic).
begin
forall i < v do in parallel
currnode ← root
minR ← 0
maxR ← valueAt(root)
while not isLeaf(currnode) do
currnode ←firstChild(currnode)
maxR ←
minR + valueAt(currnode)
if i /∈ [minR,maxR[ then
currnode ←nextSibling(currnode)
minR ←
minR + valueAt(currnode)
compact [i] ←
data[indexOf(currnode)]
end
To extract the valid elements, a search traversal
is conducted in the binary tree. This is done in par-
allel for a number v of valid elements found on the
original stream. Each traversal takes as input the in-
GRAPP 2009 - International Conference on Computer Graphics Theory and Applications
124
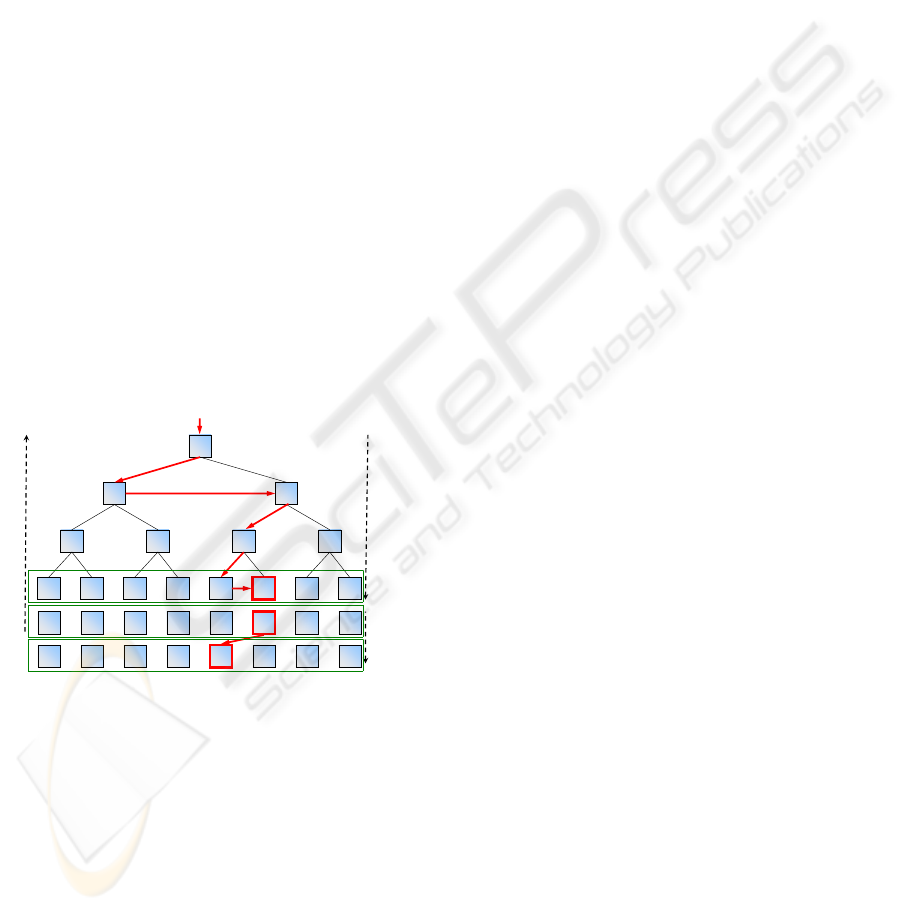
dex (order) of a valid element. Based on the infor-
mation stored by each tree node, the algorithm dy-
namically maintains the range of valid indexes under
each node. This information is used to guide the tree
traversal as follows. Beginning at the root node, and
searching for the i
th
element, the range of valid in-
dexes [minR,maxR[ is set to [0,v[. The traversal then
makes a first-child move and updates this range by
setting its bounds to [minR,minR + n[, being n the
number of valid elements under the current node. If
i is not within the range, the traversal moves to the
next-sibling node and the valid range is updated to
[minR +n,maxR[. This process is repeated until a leaf
node is reached for which the valid range comprises
the index of the sought element, i.e. [i, i +1[. The data
is then copied from that position into the i
th
position
of the compacted stream. Algorithm 5 presents the
pseudo-code of this process. An example of its op-
eration is depicted in Figure 6. The figure illustrates
the search of the 5
th
element of the stream (i = 4).
The bounds of the valid index range are shown next
to upper-left corner of each node. The path of the
search is obtained by following the (red) arrows. At
the illustrated example, the desired element is found
at index 5 of the data stream which is copied to the
corresponding position of the compacted stream (in-
dex i = 4)
next
sibling
[4,5[
6
33
1 12 2
0 101 1 1 1 1
next sibling
first child
first child
first child
[3,6[
[3,5[
[3,4[
1 - encoding/reduction
2 - traversal/search
0 f0a b c d e
a b c d e f
i=4
[0,3[
01234567
01234567
01234567
i=4
compacted data
original data
discriminated data
3 - compaction
[0,6[
Figure 6: Graphical trace of the Binary Tree algorithm.
Each search is independent and can be conducted
in parallel. The complexity of the search equals the
depth of the binary tree, i.e. log
2
(s). Note that the
search is only conducted for the v valid elements, ac-
counting a total number of search steps of v · log(s).
4 RESULTS
All the described algorithms in Section 3 were im-
plemented, tested and analyzed. A block based com-
paction mechanism, based on (Roger et al., 2007)
and with implementation details described by (Mor-
eira et al., 2009), was used in order to allow efficient
handling of large data streams.
Implementation was done under OpenGL 2.0,
making use of frame buffer objects (FBO) with sin-
gle component 32-bit float texture formats for the
input and output data and, as well, for intermedi-
ary memory buffers. Four component (RGBA) 32-
bit float formats were used for the described block
compaction mechanism. The presented results were
taken using a nVidia GeForce 7300 Go (G72M) GPU.
Fragment programs were coded using the Cg Lan-
guage (Fernando and Kilgard, 2003), but are straight-
forwardly convertible to the OpenGL Shading Lan-
guage (Kessenich, 2006). All timings were taken the
OpenGL GL_EXT_timer_query extension.
We implemented and measured the time to per-
form the all-prefix-sums using the algorithms de-
scribed by (Hillis and Steele JR, 1986) and (Blelloch,
1990) and verified that, for block sizes under 128, the
recursive doubling approach performs faster than the
balanced tree. For larger block sizes, the balanced tree
performs faster.
As the prefix sum is being done in relatively small
substreams, the overall timings are directly propor-
tional to the data-set. For instance, we verified that for
streams with 1M elements (we use the M and K suf-
fixes to denote stream sizes orders of ×2
20
and ×2
10
,
respectively) and 256K elements (512 x 512) the over-
all timings were for all methods 1/4 and 1/16 with a
deviation not greater than 5%.
To enable a better understanding of the relative
weight of each step comprised by the compaction al-
gorithms, times were taken separately as depicted in
Figure 7. The presented results were taken for a 4M
stream (2048 × 2048) using a block size of 256. Re-
sults demonstrate that the binary search process of
Horn’s algorithm dominates the overall process. The
weight of the search is larger for dense (low percent-
age of invalids) data. For sparser data, the relative
weight of the search tends to be smaller. Jumping Jack
(JJ) spends the same amount of time on the prefix-
sums, but performs faster for dense data, outperform-
ing Horns algorithm in such circumstances. RLZ
spends twice the time on the prefix-sum, but its faster
search leads to outperform Horn’s algorithm for dense
data and to be competitive for sparse data. Finally, the
Binary Tree (BT) has a very fast first stage (reduc-
tion). The extraction (search) process depends on the
tree depth and on the number of valid elements and
has a worse performance than JJ and RLZ algorithms
for dense data. However, due to the quicker first step,
the BT algorithm is able to outperform all the other,
particularly from mid to high data sparseness. We no-
NEW ALGORITHMS FOR GPU STREAM COMPACTION - A Comparative Study
125
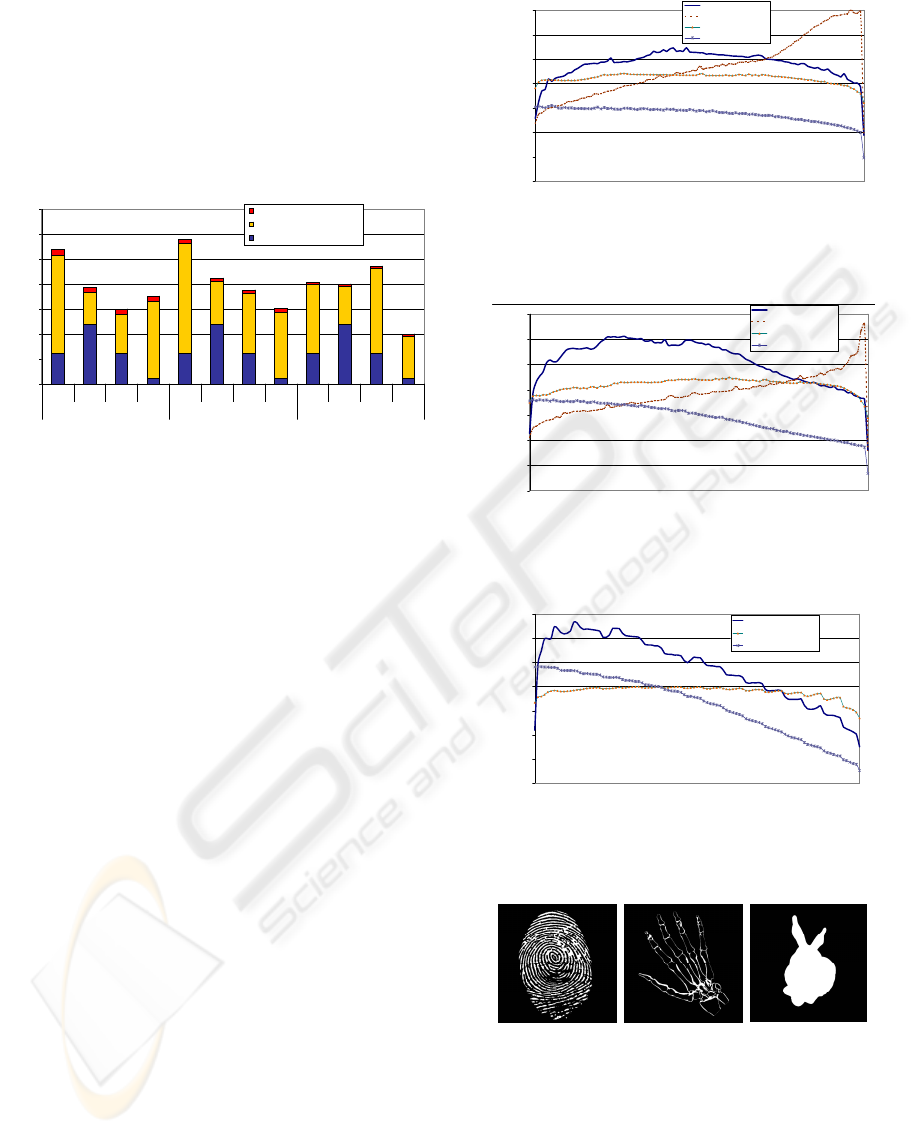
ticed that the concatenation step is comparatively very
fast, except for very small block sizes where the large
number of blocks leads to increased effort on the com-
putation of the inter-block prefix sum and on the line
rendering mechanism. As it can be observed, the con-
catenation also depends on the data distribution, but
for the used block size this has no significant impact
on the overall performance.
0
50
100
150
200
250
300
350
Horn RLZ JJ BT Horn RLZ JJ BT Horn RLZ JJ BT
10%Invalids 50%Invalids 90%Invalids
Time(ms)
Concatenation
Search/Extraction
PrefixSum/Reduction(intrablock)
Figure 7: Times (in milliseconds) needed to perform the
several stages of compaction with three different data den-
sities, using the four tested algorithms. Stream and block
sizes were 4M and 256, respectively.
Experiments using different block sizes were con-
ducted with results reported in Figures 8 to 10. A first
conclusion is that algorithms behave distinctively for
different block sizes. For dense data, Horn’s algo-
rithm takes advantage by using smaller blocks. On
the contrary, when operating with sparse data, it per-
forms faster using a larger block size. This is also the
case of the BT algorithm. The JJ and RLZ algorithms
have a more regular behavior, taking benefits, in gen-
eral, from adoption of a larger block size.
Jumping Jack algorithm can be very fast for mid to
low data densities, performing better than Horn’s for
densities of invalid elements below densities of 70%
to 80%, depending on the block size. RLZ presents
a competitive behavior, particularly for large block
sizes. Results analysis also exposes an interesting
characteristic of RLZ as it exhibits the less data de-
pendent behavior, being the more stable algorithm,
with less performance variance for the different data
densities. Such characteristic can be of importance if,
for instance, in the context of an interactive applica-
tion, a sustained and predictable frame-rate is desired.
The Binary Tree Algorithm is generally the best and,
particularly for sparse data, it outperforms all the oth-
ers, independently of the block size, exception made
to very dense data. However, different block sizes has
to be chosen a priori, depending on the data density,
in order to obtain an optimal setting. In practical set-
tings these knowledge may not be available in order
to optimally tune the compaction parameters.
To enable a better perception of the data distri-
0.00
50.00
100.00
150.00
200.00
250.00
300.00
350.00
0 102030405060708090100
DensityofInvalidElements(%)
Time(ms)
Horn'sbinarysearch
JumpingJack
RunLengthsofZeros
BinaryTree
Figure 8: Time (in milliseconds) achieved for compaction
of 4M stream, using a block size of 32.
0.00
50.00
100.00
150.00
200.00
250.00
300.00
350.00
0 102030405060708090100
DensityofInvalidElements(%)
Time(ms)
Horn'sbinarysearch
JumpingJack
RunLengthsofZeros
BinaryTree
Figure 9: Time (in milliseconds) achieved for compaction
of 4M stream, using a block size of 256.
0.00
50.00
100.00
150.00
200.00
250.00
300.00
350.00
0 102030405060708090100
DensityofInvalidElements(%)
Time(ms)
Horn'sbinarysearch
RunLengthsofZeros
BinaryTree
Figure 10: Time (in milliseconds) achieved for compaction
of 4M stream, using a block size of 2048.
Finger
83.84%Invalids
Hand
95.10%Invalids
Bunny
80.56%Invalids
Hand: brancos/pretos 205257 / 3989047 (95,1%)
Bunny 815285 (80.56%)
Finger 677803 (83.84%)
Figure 11: Thumbnails of the image data set with white
pixels corresponding to valid elements. Images and their
negatives were tested with three different sizes (256K, 1M
and 4M).
butions, we opted to present data sets comprised by
three different images and their correspondent neg-
atives (i.e. negating the validity criterion), each of
GRAPP 2009 - International Conference on Computer Graphics Theory and Applications
126

Table 1: Time (in milliseconds) achieved for compaction
of the image data set. The i_ prefix denotes the negative
version.
block
Algorithm 256K 1M 4M 256K 1M 4M
Horn 13.24 50.27 166.56 14.15 54.90 180.63
JJ 13.21 43.31 128.49 12.05 40.85 122.07
RLZ 12.66 51.61 173.38 13.52 56.05 185.19
BT
8.55 31.39 96.08 11.68 45.46 147.78
Horn 12.33 43.79 161.45 13.77 49.97 178.86
JJ 9.98 35.83 131.03 9.49 31.44 109.14
RLZ 10.21 38.55 154.62 11.19 43.26 166.62
BT
7.22 25.86 95.81 10.91 44.07 166.05
Horn 11.49 42.41 158.07 17.22 68.70 217.57
JJ
RLZ 10.85 40.15 160.83 11.91 44.85 173.98
BT
6.47 25.77 97.27 11.87 49.35 190.96
block
Algorithm 256K 1M 4M 256K 1M 4M
Horn 12.24 44.01 130.65 13.34 49.89 159.19
JJ 12.11 39.95 112.34 11.00 42.84 137.28
RLZ 12.19 50.11 164.28 13.48 55.91 189.76
BT
7.76 26.97 68.07 11.73 45.64 151.15
Horn 9.60 32.75 115.49 11.81 43.86 150.92
JJ 10.33 32.63 102.00 8.02 30.14 116.11
RLZ 9.62 36.59 141.94 11.21 43.32 171.06
BT
5.33 17.65 57.87 11.11 44.58 171.73
Horn 8.51 31.55 112.12 15.91 57.20 187.88
JJ
RLZ 10.04 37.73 145.76 11.72 44.88 176.55
BT
4.36 15.35 52.93 13.01 51.08 202.21
block
Algorithm 256K 1M 4M 256K 1M 4M
Horn 10.31 37.86 110.35 11.72 43.08 134.01
JJ 9.77 34.14 100.04 9.27 36.70 115.59
RLZ 11.75 49.33 162.55 12.92 54.05 183.24
BT
6.93 26.20 69.21 11.21 42.73 134.30
Horn 9.02 30.29 101.07 10.22 34.94 121.30
JJ 7.16 23.48 84.39 6.80 26.29 99.39
RLZ 9.30 36.26 142.47 10.48 40.99 162.45
BT
5.29 20.38 70.25 10.69 40.49 150.68
Horn 9.34 36.33 130.78 14.91 55.50 146.91
JJ
RLZ 9.76 37.28 146.67 11.02 41.87 165.98
BT
4.96 21.25 81.77 11.77 46.66 178.98
Finger i_Finger
5
7
Bunny i_Bunny
9
Hand i_Hand
5
5
7
9
7
9
them with three different resolutions: 512x512 (de-
noted as 256K); 1024x1024 (1M); and 2048 x 2048
(4M). Figure 11 depicts thumbnails of the used im-
ages, with white pixels representing valid elements,
and as well the corresponding overall data density.
As it is observable, the images have distinct spatial
frequencies with correspondence in distinct regional
data densities.
Tests were conducted using the four algorithms
and three different block sizes: 32; 128; and 512, re-
spectively. As, for the tested hardware, the maximum
loop count on fragment programs is of 256, the Jump-
ing Jack algorithm was not tested for the larger block
size. The achieved results are shown in Table 1. For
each data set, the overall best result is depicted with
bolder font and the overall best result using a mono-
tonic algorithm (i.e. excluding Jumping Jack) is rep-
resented with a darker background.
The most relevant fact revealed is that there are
distinct settings (algorithm and block size) achieving
the best performance for the different data sets. Two
major conclusion can be drawn. The first is that there
is not a general optimal setting, and the second is that
this optimal setting can only be determined with a pri-
ori knowledge about the data distribution.
The above discussion opens an interesting avenue
for research on how to explore the best of each al-
gorithm by using an optimal meta-algorithm, which
should be able to make the most appropriate choices
of the basic algorithm and block size. Several op-
tions may apply in the design of such optimized meta-
algorithm. A first approach could pursuit an adap-
tion to the expectable best performing algorithm and
block size, based on a local or regional evaluation of
the data. Thus, for the same data set, it would be
possible to choose several parameters for different re-
gions. Another approach may comprise a more low-
frequency optimization, assuming that the data may
vary along the time with some coherency. Hence, it
should be possible to optimize the algorithm in or-
der to adapt to the current pattern of the data. We
shall also notice that the algorithmic performance de-
pends on the underlying architecture of the GPU as
well (e.g. degree of parallelism, branch and loop con-
trol, granularity, etc.). Thus, the solution for a given
hardware setting may not be the more optimized for
another setting, even for identical datasets.
5 CONCLUSIONS
This paper introduces the RLZ and the Binary Tree
algorithm for parallel stream compaction. We used
these algorithms within a block based compaction
mechanism in order to handle large streams without
coordinate conversion overhead and also taking ad-
vantage from the texturing capabilities of the GPU.
We tested our proposals against existent algorithms.
The achieved results demonstrate the practical
usefulness of our proposal. The RLZ algorithm
proved to be competitive with prior algorithms, out-
performing them in some circumstances. It presents
the most data independent performance which makes
it the most stable and predictable algorithm.
The Binary Tree algorithm is globally the fastest,
taking advantage by not doing an explicit computa-
tion of the all-prefix-sum. However, we have also ob-
served from the experiments that, for real data-sets, an
optimal choice on the algorithm and parameters is not
obvious and may require some knowledge on the data
distribution, not only on a global basis but also on a
local or regional basis. In this context, we outlined
a meta-algorithm able to adapt to the data in order to
have an optimized performance. As future work, we
plan to further research on this topic.
Our implementations have room to be further op-
NEW ALGORITHMS FOR GPU STREAM COMPACTION - A Comparative Study
127

timized. We plan to continue testing the algorithms
in a broader range of hardware platforms and diversi-
fied data sets, expecting further insights that can lead
to improved variations and ideas, and so, another av-
enue to future work focus on how these algorithms
and concepts adapt to new architectures and forth-
coming standards.
ACKNOWLEDGEMENTS
This work has been partially supported by
European Social Fund program, public con-
test 1/5.3/PRODEP/2003, financing request no.
1012.012, medida 5/acção 5.3 - Formação Avançada
de Docentes do Ensino Superior, submitted by
Escola Superior de Tecnologia e Gestão do Instituto
Politécnico de Viana do Castelo.
REFERENCES
Blelloch, G. (1990). Prefix sums and their applications.
Technical Report CMU-CS-90-190, Carnegie Mellon
University - CMU – School of Computer Science,
Pittsburgh, PA 15213.
Crow, F. C. (1984). Summed-area tables for texture map-
ping. In SIGGRAPH ’84: Proceedings of the 11th
annual conference on Computer graphics and interac-
tive techniques, pages 207–212, New York, NY, USA.
ACM.
Fernando, R. and Kilgard, M. J. (2003). The Cg Tuto-
rial: The Definitive Guide to Programmable Real-
Time Graphics. Addison-Wesley Longman Publishing
Co., Inc., Boston, MA, USA.
GPGPU (2008). GPGPU.org. http://www.gpgpu.org, last
visited 2008.07.22.
Greß, A., Guthe, M., and Klein, R. (2006). GPU-based
collision detection for deformable parameterized sur-
faces. Computer Graphics Forum, 25(3):497–506.
Harris, M., Sengupta, S., and Owens, J. D. (2007). Parallel
prefix sum (scan) with CUDA. In Nguyen, H., editor,
GPU Gems 3, chapter 39. Addison Wesley.
Hensley, J., Scheuermann, T., Coombe, G., Singh, M., and
Lastra, A. (2005). Fast summed-area table generation
and its applications. Computer Graphics Forum (Pro-
ceedings of Eurographics), 24(3):547–555.
Hillis, W. D. and Steele JR, G. (1986). Data parallel algo-
rithms. Communications of the ACM, 29(12):1170–
1183.
Horn, D. (2005). GPU Gems 2, chapter Stream reduction
operations for GPGPU applications, pages 573–589.
Addison-Wesley.
Kessenich, J. (2006). The OpenGL Shading Language
(v.1.20). OpenGL Architecture Review Board. avail-
able at http://www.opengl.org/documentation/glsl/.
Lefohn, A. E., Sengupta, S., and Owens, J. D. (2007). Res-
olution matched shadow maps. ACM Transactions on
Graphics, 26(4):20:1–20:17.
Moreira, P. M., Reis, L. P., and de Sousa, A. A.
(2009). Jumping jack : A parallel algorithm for non-
monotonic stream compaction. In GRAPP 2009 - 4th
International Conference on Computer Graphics The-
ory and Applications, February 5–8, Lisbon, Portugal.
Nickolls, J., Buck, I., Garland, M., and Skadron, K. (2008).
Scalable parallel programming with CUDA. ACM
Queue, 6(2):40–53.
OpenGL Architecture Review Board (2008).
ARB_geometry_shader4 Extension Spec-
ification. OpenGL Architecture Re-
view Board, rev 22 edition. available at
http://www.opengl.org/registry/specs/ARB/
geometry
s
hader4.txt.
Owens, J. D., Luebke, D., Govindaraju, N., Harris, M.,
Kruger, J., Lefohn, A. E., and Purcell, T. J. (2007).
A survey of general-purpose computation on graphics
hardware. Computer Graphics Forum, 26(1):80–113.
Roger, D., Assarsson, U., and Holzschuch, N. (2007). Whit-
ted ray-tracing for dynamic scenes using a ray-space
hierarchyon the GPU. In Proceedings of the Euro-
graphics Symposium on Rendering’07, pages 99–110.
Segal, M. and Akeley, K. (2006). The OpenGL
Graphics System: A Specification (Version
2.1). http://www.opengl.org/documentation/specs/
version2.1 (last visited 2008.07.24).
Sengupta, S., Lefohn, A. E., and Owens, J. D. (2006).
A work-efficient step-efficient prefix sum algorithm.
In Proceedings of the Workshop on Edge Comput-
ing Using New Commodity Architectures, May 23–24,
Chapel Hill, North Carolina, USA, pages D:26–27.
Ziegler, G., Tevs, A., Theobalt, C., and Seidel, H. (2006).
Gpu point list generation through histogram pyramids.
In 11th International Fall Workshop on Vision, Mod-
eling, and Visualization - VMV’06, pages 137–144.
GRAPP 2009 - International Conference on Computer Graphics Theory and Applications
128
