
JUMPING JACK
A Parallel Algorithm for Non-Monotonic Stream Compaction
Pedro Miguel Moreira
1,2
, Luís Paulo Reis
2,3
and A. Augusto de Sousa
2,4
1
ESTG-IPVC, Instituto Politécnico de Viana do Castelo, Viana do Castelo, Portugal
2
DEI/FEUP, Faculdade de Engenharia da Universidade do Porto, Porto, Portugal
3
LIACC, Laboratório de Inteligência Artificial e Ciência de Computadores, Porto,Portugal
4
INESC-Porto, Instituto de Engenharia de Sistemas e Computadores do Porto, Portugal
Keywords:
Stream Compaction, Parallel Algorithms, Parallel Processing, Graphics Hardware.
Abstract:
Stream Compaction is an important task to perform in the context of data parallel computing, useful for many
applications in Computer Graphics as well as for general purpose computation on graphics hardware. Given
a data stream containing irrelevant elements, stream compaction outputs a stream comprised by the relevant
elements, discarding the rest. The compaction mechanism has the potential to enable savings on further
processing, memory storage and communication bandwidth. Traditionally, stream compaction is defined as
a monotonic (or stable) operation in the sense that it preserves the relative order of the data. This is not
a full requirement for many applications, therefore we distinguish between monotonic and non-monotonic
algorithms. The latter motivated us to introduce the Jumping Jack algorithm as a new algorithm for non-
monotonic compaction. In this paper, experimental results are presented and discussed showing that, although
simple, the algorithm has interesting properties that enable it to perform faster than existent state-of-the-art
algorithms, in many circumstances.
1 INTRODUCTION
Current Graphics Processing Units (GPUs) are pro-
grammable parallel platforms which provide high
computational power with very large memory band-
width at low cost. These features make them com-
pelling not only under the graphics domain but also
for computationally intensive general purpose tasks,
leading to a relatively new research area focused
on mapping general purpose computation to graph-
ics processing units - GPGPU (Owens et al., 2007;
GPGPU, 2008).
Stream compaction, also designated as stream
non-uniform reduction and also as stream filtering,
takes a data stream as input, uses a discriminator to
select a wanted subset of elements, outputs a com-
pacted stream of the selected elements, and discards
the rest.
Several computer graphics applications, making
use of the GPU programmable architecture, may ben-
efit from stream compaction. Exclusion of non-
-relevant elements permits savings on further compu-
tational tasks, better memory footprints, and reduced
overhead when transferring data from the GPU to the
CPU. Stream compaction is also a fundamental com-
ponent on algorithms dealing with data partitioning
(e.g. some sorting algorithms and space hierarchies).
Parallel stream compaction is typically based on an-
other fundamental data parallel primitive, the parallel
prefix sum (Blelloch, 1990).
Conventionally, stream compaction is referred as
an order-preserving (or monotone) operation, i.e. the
output preserves the relative order of the elements.
In some circumstances, this can be a rather restric-
tive requirement. There are applications where mono-
tonicity is not fundamental, as when the data is self-
indexed (e.g. the data have coordinates, or a color
index) or when the relative order is irrelevant to fur-
ther processing. Therefore, we clearly distinguish two
classes of stream compaction: monotonic compaction
and non-monotonic compaction. The latter class mo-
tivated us to design the herein introduced Jumping
Jack algorithm.
Divide-to-conquer strategies, such as segmented
prefix-sum (Blelloch, 1990; Sengupta et al., 2007)
and hierarchical stream compaction (Roger et al.,
137
Moreira P., Reis L. and de Sousa A. (2009).
JUMPING JACK - A Parallel Algorithm for Non-Monotonic Stream Compaction.
In Proceedings of the Fourth International Conference on Computer Graphics Theory and Applications, pages 137-146
DOI: 10.5220/0001785001370146
Copyright
c
SciTePress
2007) allow for processing large amounts of data and
lead to increased efficiency.
The herein introduced Jumping Jack algorithm
makes use of a similar strategy, Block Stream Com-
paction; it first splits the input into regular smaller
blocks of data, compacts them, and finally concate-
nates the partial results into the desired compacted
output stream. The block concatenation step uses the
vertex engine and the texturing units of the GPU, in
order to achieve a better computational complexity
with respect to a global compaction approach.
The rest of the paper is organized as follows.
Next section introduces some fundamental concepts
and terminology on programmable graphics hard-
ware. Section 3 reviews relevant prior work on scan
primitives and stream compaction. The proposed
Jumping Jack algorithm is presented in Section 4 and
relevant details on the implementation are given in
Section 5. The achieved results are presented and dis-
cussed in Section 6. Major conclusions are summa-
rized in Section 7 alongside with possible directions
to future work.
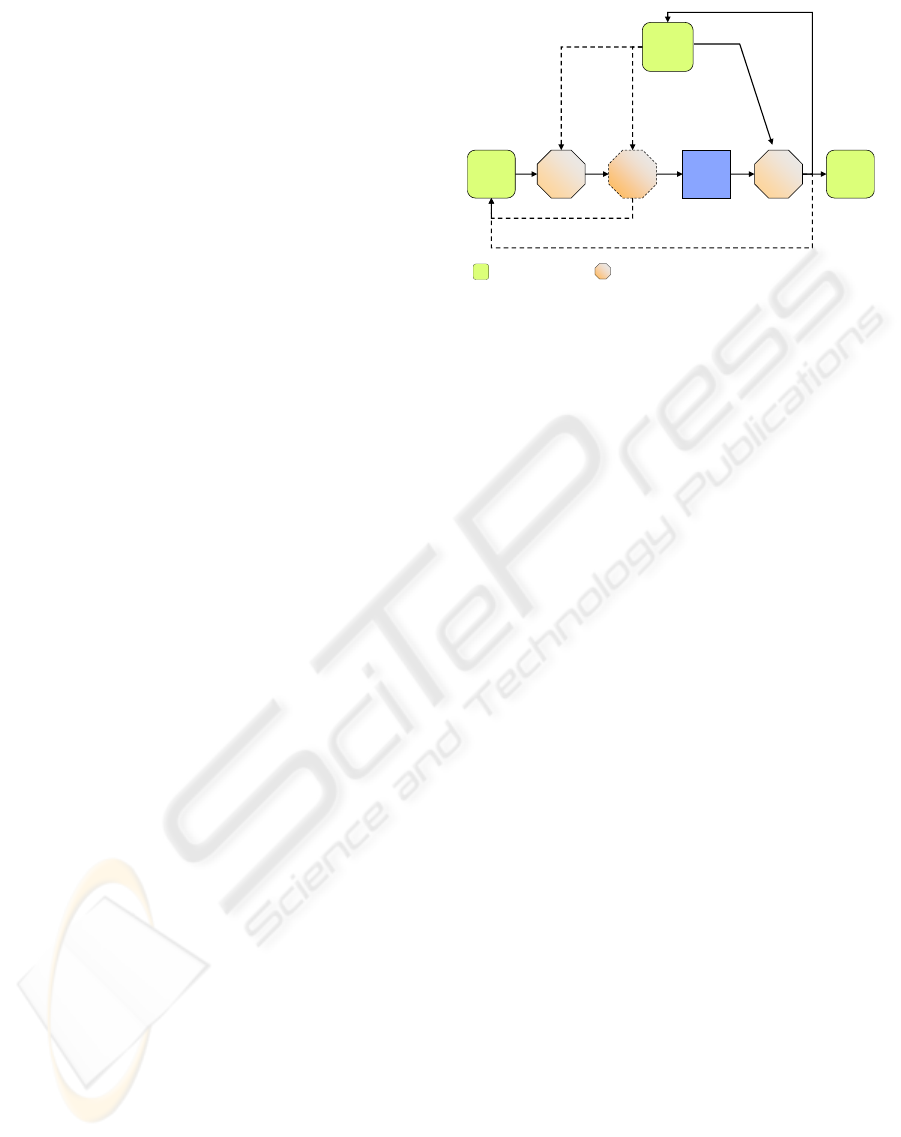
2 PROGRAMMABLE GPU
ARCHITECTURE
Here we briefly introduce some fundamental con-
cepts and terminology exhaustively used through the
paper. The current OpenGL specification (OpenGL
2.1) exposes two GPU programmable units: the
vertex and the fragment processors. A third pro-
grammable unit, the geometry processor, was recently
exposed through OpenGL extensions but it has lim-
ited support and it is only available on very recent
GPUs. GPUs are designed with several vertex and
fragment processor units, enabling high levels of par-
allelism. Vertex and fragment programs can be coded
in high level languages such as the OpenGL Shad-
ing Language (aka GLSL), HLSL and Cg, to name
the most popular. A simplified scheme of the pro-
grammable pipeline is presented in Figure 1.
A vertex program processes each vertex indepen-
dently. The vertex processor has the ability of modi-
fying the vertex positions, which can be used to redi-
rect the output to a desired position, giving it memory
scattering abilities (indirect writing). . Memory gath-
ering (indirect read) is possible at the vertex proces-
sor through texture fetching. Although conceptually
interesting, the traditionally reduced number of vertex
pipelines, the limited support for texture formats and
the unoptimized read accesses (with big latency), im-
pose limitations on the practical utility of such gath-
ering mechanism.
Frame
Buffer
Vertex
Buffer
Texture
Memory
Vertex
Processors
Geometry
Processors
Fragment
Processors
Rasterizer
RTT:
RendertoTexture
VTF:
Vertex Texture Fetch
RTVA/RTVB
RendertoVertex Array /Buffer
memory /bufferobjects programmable units
Transform Feedback
Figure 1: Simplified GPU programmable pipeline (as ex-
posed by OpenGL). Dotted units and paths have limited /
non standard support.
At the fragment processor, each fragment is pro-
cessed independently, with the fragment final posi-
tion being pre-determined before the fragment is pro-
cessed. Therefore, the fragment processor does not
have scatter abilities. However, gathering is possible
through texture fetching. A fragment program is al-
lowed to render to texture target (RTT) and also to
render to multiple targets (MRT), enabling it to easily
re-use results from one pass to another. Rendering
directly to the vertex buffer (RTVB) is not a widely
supported mechanism, although it can be indirectly
achieved in several ways.
Recently, GPU manufacturers adopted the so-
called unified architecture model, comprising sev-
eral (dozens to hundreds) of indistinct stream proces-
sors. Furthermore, global load-store memory, shared
memory for threads running on the same multipro-
cessor and synchronization mechanisms, are some of
the available capabilities. However, such capabilities
have only been exposed through manufacturer depen-
dent application programming interfaces (APIs) and
tools (e.g. such as nVidia CUDA (Nickolls et al.,
2008)), without support by architecture independent
or by general purpose APIs.
The herein proposed algorithm is intended to al-
low implementations making use of widely supported
GPU capabilities, such as the exposed by OpenGL.
It is assumed that the GPU has programmable ver-
tex processors with scatter and (potentially limited)
gather abilities and programmable fragment proces-
sors with gather abilities but without scatter.
3 RELATED WORK
This section reviews relevant prior work on stream
compaction. As existent algorithms are typically
GRAPP 2009 - International Conference on Computer Graphics Theory and Applications
138
based on prefix-sums, we begin by introducing the
fundamental concepts and algorithms for parallel pre-
fix sum and segmented prefix-sum in the first two sub-
sections, with a special focus on their GPU imple-
mentation. The following subsection describes paral-
lel stream compaction and approaches to implement
it.
3.1 Prefix-Sum
The prefix-sum primitive (aka scan operation and also
as prefix-reduction) is probably one of the most im-
portant primitives for parallel computing (Sengupta
et al., 2007). This can be somewhat surprisingly, as
the prefix-sum primitive is mostly unnecessary on se-
quential computation. Prefix-sum is successfully used
as a fundamental strategy in the parallelization of al-
gorithms that seem to be inherently sequential (Hillis
and Steele JR, 1986; Blelloch, 1990).
The all-prefix-sum (or inclusive prefix-sum) oper-
ation (Blelloch, 1990) takes a binary associative op-
erator ⊕ and an ordered set of elements (e.g. an array
or stream) [a
0
, a
1
, . . . , a
s−1
] and returns an ordered set
[a
0
, (a
0
⊕ a
1
), . . . , (a
0
⊕ a
1
⊕ ... ⊕ a
s−1
)].
Typical prefix-sum operations use addition, maxi-
mum, minimum, product and logic operators, but any
associative operator can be used. In the rest of this pa-
per, addition will be used as the default operator for
prefix-sum.
On sequential architectures, the all-prefix-sum op-
eration is trivially implemented with linear time com-
plexity O (s) using a single pass over the data. How-
ever, parallel computation of the all-prefix-sum can
not be straightforwardly mapped from the sequential
algorithm. Observe that each output depends on sev-
eral input elements, as for instance, the computation
of the prefix-sum at the last element (rightmost) in-
volves all the others.
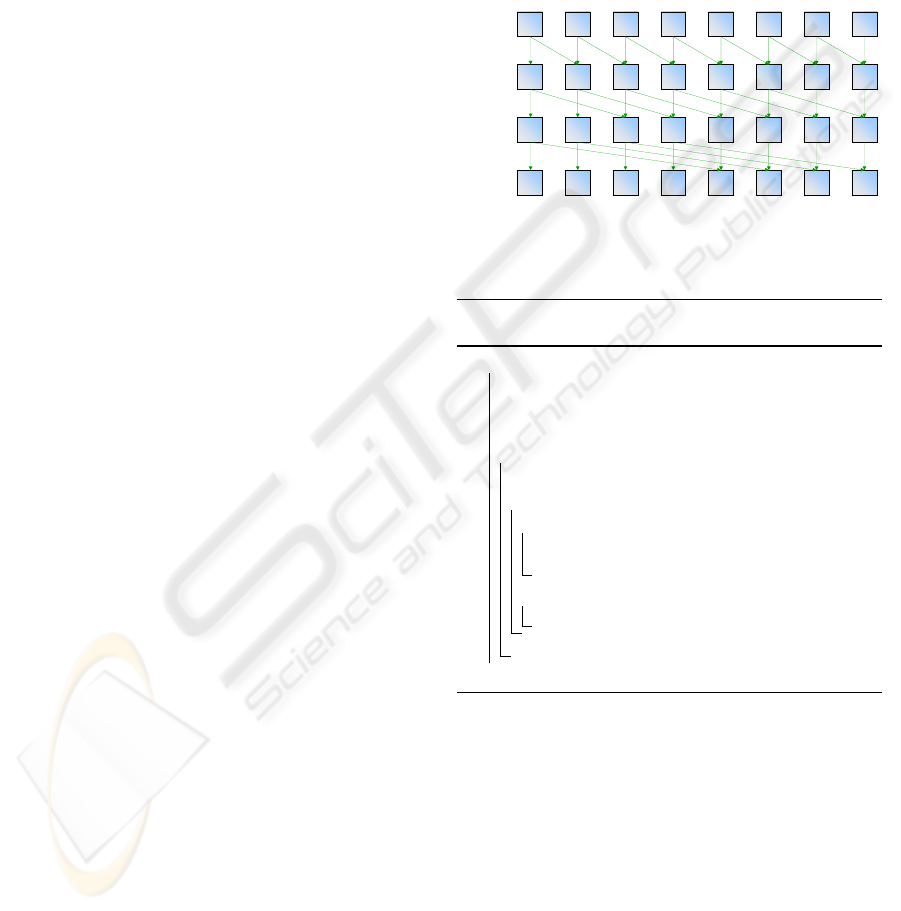
Horn (Horn, 2005) proposed a GPU implementa-
tion for a linear all-prefix-sum primitive based on a
parallel recursive doubling algorithm as described by
Hillis & Steele (Hillis and Steele JR, 1986) that is of-
ten utilized in parallel and high performance comput-
ing. Hensley et al. (Hensley et al., 2005) also used a
parallel recursive doubling algorithm to carry out fast
GPU based generation of summed area tables (SAT).
SAT generation extends the recursive doubling into a
2D data structure by operating in two directions.
The recursive doubling approach proceeds as fol-
lows. For each element, and in parallel, the algorithm
starts by summing to each element the value of the el-
ement placed one position to the left. In the next iter-
ation, each element will sum itself to the value stored
two positions to the left. By now, each record stores
the sum of four original values, from its own position
to three positions to the left; following iterations re-
curse the process doubling the offset to the left. For a
stream with size s, the algorithm iterates log
2
(s) times
to complete. If there is a number of processors that
equals the size s of the stream, the algorithm com-
pletes in O(log(s)) time leading to a total work of
O(s · log(s)). A graphical depiction of this process
is illustrated in Figure 2.
offset = 2
k
if a
k-1
[i] >= offset then
a
k
[i] = a
k-1
[i] + a
k-1
[i+offset]
else
a
k
[i] = a
k-1
[i]
1 111 0 0 1 0
1 212 1 0 1 1
1 322 2 2 2 1
1 542 2 2 3 3
data
p=2,offset=2
p=1,offset=1
p=3,offset=4
Figure 2: Parallel Prefix Sum using a recursive doubling
algorithm for a stream with s = 8 elements.
Algorithm 1: Double Buffered Parallel All-
Prefix-Sum.
begin
input : s : stream length
input : pSum[in][ ] : input data stream
output: pSum[in][ ] : all-prefix-sum stream
for p ← 1 to log
2
(s) do
o f f set = 2
p−1
forall i < s in parallel do
if i ≥ o f f set then
pSum[out][i] ←
pSum[in][i − o f f set] ⊕ pSum[in][i]
else
pSum[out][i] ← pSum[in][i]
swapBuffers(in,out)
end
As the GPU programming model does not allow
for concurrent read and write on the same memory
buffer, the usual workaround comprises using double
buffered memory, i.e. two temporary streams (tex-
tures) and making one of them the input (for read-
only accesses by means of texture fetching, which
may be done concurrently) and the other the output
(the render-target with write-only access). After each
pass, the role of these buffers are swapped. The tech-
nique is commonly mentioned as ping-pong. Algo-
rithm 1 presents pseudo-code for a double buffered
version of the recursive doubling algorithm, closer to
a OpenGL/GPU implementation.
JUMPING JACK - A Parallel Algorithm for Non-Monotonic Stream Compaction
139
Even though widely used, the GPU recursive dou-
bling algorithm can result work-inefficient. As, for
large streams, there is a number of processors typ-
ically smaller than the stream size, the computation
has to be serialized into batches. A key observation
is that the recursive doubling algorithm does unnec-
essary computations at each element.
Sengupta et al. (Sengupta et al., 2006) noticed this
fact and developed a work efficient prefix-sum algo-
rithm for GPU implementation with work complex-
ity of O(s). Their algorithm uses a balanced tree ap-
proach adapted from the algorithm presented by Blel-
loch (Blelloch, 1990). An algorithm also with O(s)
work complexity, specially devoted to 2D data, has
been independently developed by Greß et al. (Greß
et al., 2006).
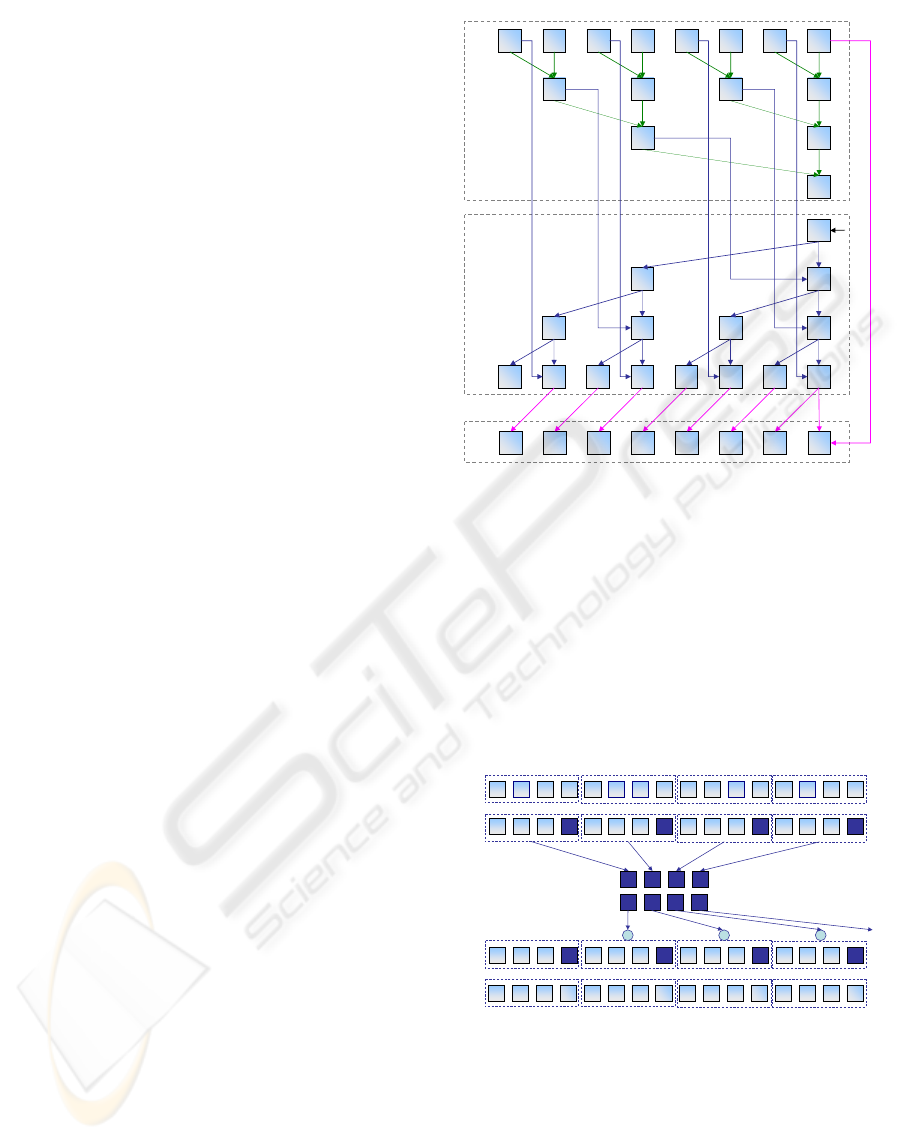
Blelloch proposes a two stage approach to com-
pute an exclusive-prefix-sum using a binary tree struc-
ture. The first, the up-sweep, is a binary reduction . At
each tree level, each node stores the sum of its chil-
dren. Notice that for each subsequent level the num-
ber of active elements/processors is halved, leading
to a total of s− 1 active processors. The second stage,
referred as down-sweep, introduces the identity value
(zero, for the addition) at the root node and then pro-
ceeds, level by level, updating the final result based on
the partial results computed during the reduction step.
Again, the number of active processors is s − 1, lead-
ing to an overall work complexity of O(s). Although
with better work efficiency, the number of passes in a
typical GPU implementation requires twice the num-
ber of passes to complete, i.e. 2· log
2
(s), compared to
the recursive doubling algorithm. Actually, the algo-
rithm, as described, computes a exclusive prefix-sum.
A final adjustment step is needed in order to compute
the all-prefix-sum. This can be carried out by shifting
all the elements one position to the left and placing the
total sum at the rightmost element. Figure 3 visually
illustrates the algorithm operation.
Sengupta et. al (Sengupta et al., 2006) observed
that the balanced tree based algorithm has few ac-
tive processors in passes / iterations that are close to
the root and does more passes than the recursive dou-
bling. The authors have proposed an hybrid algorithm
that switches from the balanced tree into a recursive
doubling approach when the number of active proces-
sors falls under the degree of parallelism (the maxi-
mum number of available parallel processors).
3.2 Segmented Prefix-Sum
The underlying strategy of segmented all-prefix-sum
is a divide-to-conquer approach. A stream of ele-
ments can be partitioned into contiguous substreams
1 111 0 0 1 0
22 0 1
32
5
0
20
30 2 2
0 431 2 2 2 3
0
1 542 2 2 3 3
up-sweep
down-sweep
final adjustment
01234567
0123
01
0
0
01
0123
01234567
01234567
p=1
p=2
p=3
p=2
p=1
p=0
Figure 3: Parallel Prefix Sum using a balanced binary tree
algorithm (after (Blelloch, 1990)) for a stream with s = 8
elements.
(known as segments or blocks) and the all-prefix-sum
is computed for each sub-stream (intra-segment sum).
Then, an inter-segment all-prefix-sum is conducted
using as input the last sum of each segment. The re-
sults of the inter-segment sum are used to offset all
the values of the next segment. The process is illus-
trated in Figure 4. Segmented prefix-sum allows for
efficient handling of large streams.
04623 5 71 8121410 11 13 159
original data
1 3 02 0 4 00 0 4 13 3 1 01
04623571 8121410 11 13 159
04623 5 71 8121410 11 13 159
intra-segment all-prefix-sum
1 3 73 3 7 71 0 4 64 7 5 61
3 7 67
3 17 2310
inter-segment all-prefix-sum
1 6 103 3 10 101 10 21 2314 17 22 2311
global all-prefix-sum
04623 5 71 8121410 11 13 159
intra-segment all-prefix-sum
1 3 73 3 7 71 0 4 64 7 5 61
+ + +
Figure 4: Segmented Parallel Prefix Sum for a stream with
s = 16 elements and segments (blocks) with b = 4 elements.
3.3 Stream Compaction
Stream compaction is an operator that takes a data
stream as input, uses a discriminator to select a valid
subset of elements, and outputs a compacted stream
of the selected elements, discarding the rest. Sequen-
tial stream reduction is trivially implemented in O(s)
GRAPP 2009 - International Conference on Computer Graphics Theory and Applications
140

with a single pass over the data.
Parallel stream compaction is an important opera-
tion for several applications. Examples in the graph-
ics domain that benefit from stream compaction in-
clude collision detection (Greß et al., 2006), ray-
tracing (Roger et al., 2007), shadow mapping (Lefohn
et al., 2007), point-list generation (Ziegler et al.,
2006) and, in general, all algorithms that make use
of data partitioning.
While seeming an inherently sequential computa-
tion, stream compaction can be parallelized using the
all-prefix-sum. The fundamental idea is to discrim-
inate data using a value of one to mark invalid ele-
ments and zero to mark valid elements. Then, the
all-prefix-sum of this discriminated stream is com-
puted. The resulting stream stores, for each position,
the number of invalid elements to the left. This value
corresponds to the displacement to the left that each
valid element has to undertake in order to build the
compacted stream (see Figure 5).
04623 5 71 8121410 11 13 159
original data
discriminated data
all-prefix-sum
compacted data
0 0 db 0 c 0a 0 0 0e 0 f 00
1 1 00 1 0 10 1 1 10 1 0 11
1 3 31 2 3 41 5 8 96 7 8 106
a e dc d f 0b 0 0 0e 0 f 00
04623 5 71 8121410 11 13 159
04623 5 71 8121410 11 13 159
04623 5 71 8121410 11 13 159
Figure 5: Compaction of a stream based on the all-prefix-
sum.
For parallel architectures with scattering abilities,
the compaction process could be implemented in a
single pass, writing the valid elements to their fi-
nal positions using the displacements available from
the all-prefix-sum (Sengupta et al., 2007). As no-
ticed, scattering is not available at the fragment pro-
cessor. Consequently, scatter has to be converted to
gather through vertex texture fetching (VTF), addi-
tional passes or search (Harris, 2005; Horn, 2005).
A straightforward solution to parallel compaction
might also make use of GPU based sorting. Although,
GPU-sorting solutions are typically based on sorting
networks and variations of bitonic search yielding to
an overall computational complexity of O(log
2
(s))
(refer to (Owens et al., 2007) for a comprehensive sur-
vey on GPGPU). Horn (Horn, 2005) noticed this and
proposed an improved algorithm from stream com-
paction. His algorithm improves the overall complex-
ity by a factor of log(s) yielding to an overall com-
plexity of O(log(s)). The solution is based on the
observation that the all-prefix-sum (pSum[ ]) is an as-
cending sorted stream and, as a result, a search can
be conducted on the all-prefix-sum stream, in order
to find the positions corresponding to the elements
that will comprise the output compacted stream. The
fundamental idea is to conduct, in parallel, a binary
search, for all the first c indexes (where c ≤ v, with v
denoting for the number of valid elements), in order
to find an index f that satisfies f = c + pSum[ f ] and
for which the original data stream has a valid element
(Horn, 2005). The solution avoids the need of scatter-
ing, which is converted to gathering through search,
with a computational complexity of order O(log(s))
and total work of order O(s · log(s)).
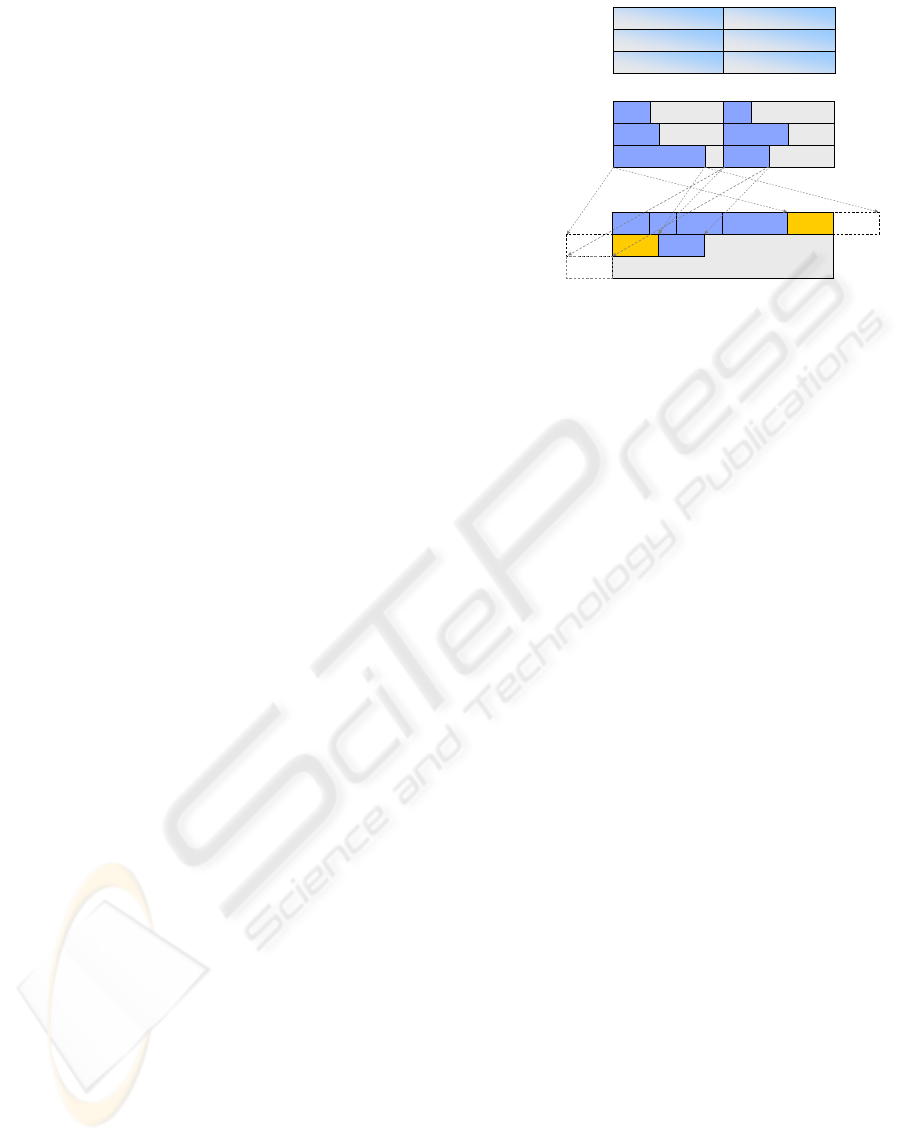
3.4 Block Stream Compaction
Similarly to segmented prefix-sum, a divide to con-
quer strategy can be applied to compaction, as the hi-
erarchical compaction scheme proposed by Roger et.
al. (Roger et al., 2007) (Figure 6). The stream can be
segmented in blocks, the compaction process is done
for each block, and then a second-level process re-
computes an overall compacted stream based on the
inter-segment all-prefix-sums. As, subsequently to
the inner block compaction, the valid elements are
contiguously stored, the inter-block prefix-sum gives
the displacement to apply to each compacted sub-
stream. The concept is easily extended to a hierar-
chical process, and any prefix-sum or compaction al-
gorithm may apply.
split into blocks
compact compact compact compact compact
concatenation
inputstream
blocks
compacted blocks
compacted outputstream
Figure 6: The block based compaction approach (after
(Roger et al., 2007)).
As large streams are mapped into 2D textures, an
immediate benefit from the block based compaction
arises from avoiding massive 1D ↔ 2D coordinate
conversions. A line by line, or segment by segment
computation avoids these conversions, but a final step
must be attained in order to concatenate the com-
pacted parts of the blocks into a global compacted
stream. As all elements of each compacted block
must displace the same amount to the left, texture
mapping can be used, with expected linear work, to
attain such goal without the need for a scatter to gather
conversion.
JUMPING JACK - A Parallel Algorithm for Non-Monotonic Stream Compaction
141

4 JUMPING JACK ALGORITHM
This section introduces an original algorithm for non-
monotonic compression, i.e. the relative order of the
valid elements is not preserved on the output. The
algorithm was named Jumping Jack after observing
the pattern of the search process that seems to consec-
utively jump forwards and backwards on the stream
(Figure 7).
Although its simplicity, it has very interesting
properties alongside with some limitations. We will
discuss how these limitations can be mitigated leading
to a suitable implementation on the GPU, turning it
competitive or faster than existing stream compaction
algorithms.
For a stream with size s with v valid elements, the
idea is to keep the valid elements positioned within
the first v indexes and fill the remaining positions
(holes) by finding valid elements in the rest of the
stream.
For each stream element, the all-prefix-sum has
the ability to communicate some information about
the past elements (e.g. number of non valid ele-
ments to the left). Thus, for each position, given the
known non-valid elements to the left, one can com-
pute the potential maximum size of the compacted
stream (this number can also be interpreted as the
first index that undoubtedly will not be part of the
compacted stream). We refer this index as the max-
allowable-size (MAS). MAS is easily evaluated as the
difference of the stream size by the all-prefix-sum
(Equation 1). Computation of the MAS stream can
be done explicitly by a straightforward adaptation of
the the all-prefix-sum computation, or embedded in
the algorithm.
MAS[i] = s − pSum[i]; (1)
The search proceeds as follows. For a given in-
dex i within the first v positions, if the original data
is valid, then the corresponding value is copied to the
final stream. Otherwise, the algorithm uses the MAS
value at position i and jumps to the corresponding in-
dex. This will be the first index where valid elements
may be found. The process is then repeated until a
valid element is found. The pseudo-code for the algo-
rithm is given in Algorithm 2.
Applied to each position, the algorithm has the
ability to find all the remaining valid elements (i.e.
there is a one-to-one mapping between the first v po-
sitions and the positions of the valid elements).
To enable a better understanding of the algorithm,
a visual trace of its operation for a stream with 6 valid
elements in a total of 16 is depicted in Figure 7. As it
can be observed, there are three valid elements within
Algorithm 2: Jumping Jack (no order preserv-
ing).
input : s : the stream length
input : data[ ] : the data stream
input : MAS[ ] : the max-allowable-size stream
output: compact[ ] : the compacted stream
begin
v ← MAS[s − 1]
forall i < v in parallel do
idx ← i
while data[idx] is not valid do
idx ← MAS [idx];
compact [i] ← data[idx]
end
the first 6 positions (at indexes 1, 2 and 5, respec-
tively), which will keep their positions. For the other
positions (indexes 0, 3 and 4) a search for valid ele-
ments is conducted based on the MAS values. These
positions find their valid elements after 2, 7 and 1
search steps, respectively.
idx = i;
while(data[idx] == 0)
idx = width - pSum[idx];
return data[idx];
i=0,
idx = 0, data[0]=0, not found
idx = 16 – pSum[0] = 15, data[15] = 0, not found
idx = 16 – pSum[15] = 6, data[6] = d, found @ 6
…
i=3,
idx = 3, data[3] = 0, not found
idx = 16 – pSum[3] = 14, data[14] = 0, not found
0 0 db 0 c 0a 0 0 0e 0 f 00
04623571 8121410 11 13 159
d f db e c 0a 0 0 0e 0 f 00
1 1 00 1 0 10 1 1 10 1 0 11
15 13 1315 14 13 1215 11 8 710 9 8 610
0 0 db 0 c 0a 0 0 0e 0 f 00
1 3 31 2 3 41 5 8 96 7 8 106
original data
discriminated data
all-prefix-sum
MAS
original data
compacted data
Figure 7: Graphical trace of the Jumping Jack algorithm.
The fundamental property of this algorithm is that,
for any given position, it will find a different valid
element. Other very interesting property is that the
parallel work (the sum of the work carried out by all
processors) is linear and upper bounded by s-v search
steps.
Nevertheless, for very sparse data, this work can
be imbalanced, i.e. for some positions, finding a valid
element will take much more work than others. The
worst case happens when a unique valid element ex-
ists, and it is positioned in the middle of the stream.
In such case, s − 1 search steps will be needed to find
it.
GRAPP 2009 - International Conference on Computer Graphics Theory and Applications
142
Theoretically, and if an arbitrary large number of
processors is available, the algorithm is inefficient,
as the overall computation only completes as the last
parallel processor finishes its operation. Therefore, in
the worst case, the parallel cost will be of quadratic
order. This constitutes the algorithm major weakness.
In practice, there is not an unlimited number of
fragment processors on the GPU. Therefore, the com-
paction of large streams has to be serialized into
batches to the available processors mitigating the pos-
sibly imbalanced behavior of the algorithm.
To further limit the influence of this undesirable
property, we make use of a segmented compaction
strategy in order to bound the maximum number of
iterations that may be performed by each element (by
reducing the size of the individual streams to com-
pact, as described in Section 3.4).
From the above discussion one can expect that,
for not very sparse data distributions, the algorithm
can be very fast in finding the unpositioned valid ele-
ments.
5 IMPLEMENTATION
Implementation was done using OpenGL 2.0, mak-
ing use of FBOs (frame buffer objects) with single
component 32-bit float texture formats for the input
and output data, as well as, for intermediary memory
buffers. Four component (RGBA) 32-bit float for-
mats were used for the described block compaction
mechanism. The presented results were taken using
a nVidia GeForce 7300 Go (G72M) GPU. Fragment
programs were coded using the Cg Language, but are
straightforwardly convertible to GLSL. All timings
were taken at GPU side using the query mechanism
provided by the OpenGL GL_EXT_timer_query ex-
tension.
The Jumping Jack Algorithm (Section 4) was im-
plemented to be used by a block based compaction
mechanism (Section 3.4). For the MAS computation
we implemented both the recursive doubling (Hillis
and Steele JR, 1986) and balanced tree (Blelloch,
1990) algorithms (Section 3.1).
We adopted (Roger et al., 2007) ideas to imple-
ment the block based compaction mechanism. The
process is depicted by Figure 8 and comprises three
stages.
The first two stages are straightforward. The sec-
ond stage can use any compaction algorithm. We only
notice that the number of invalid elements per block
must be provided as a result from the second stage
(e.g. the value of the all-prefix-sum at the last block
element). We will now detail on the third stage which
B1 B2 B3
B5_1
B0 B4_1
B4_2
B0 B1
B2 B3
B4 B5
B0 B1
B2 B3
B4 B5
stage 1: map
stream to2Dtexture
and split into regular
size (line‐aligned)
blocks
stage 2: compact
each block
stage 3:
concatenation,using
compacted blocks as
atexture map and
rendering textured
lines.
B5_2
Figure 8: Block Based Compaction implementation.
is more elaborated.
Given the number of invalid elements per block,
the displacements, for each of the block compacted
substreams, can be computed using an a inter-block
all-prefix-sum. These displacements have to be con-
verted from 1D coordinates to 2D coordinates from
which the (x, y) coordinates for the two endpoints of
each block are obtained. As it is shown (Figure 8,
block B4) there are compacted blocks that may wrap
between consecutive lines in the result. Notice that
these have not to be split in more than two parts (as
the block size is less or equal than the line width).
To simplify, we assumed that all compacted blocks
wrap and actually we compute four endpoints corre-
sponding to the start and end positions of the first sec-
tion and the (potential) second section. Texture coor-
dinates are assigned to each endpoint in accordance
with the compacted substream position.
These values are intended to be used by the ge-
ometry engine. This is actually implemented using a
Render to Vertex Array (RTVA) technique, but other
options exist as outlined later in the text. As the num-
ber of lines to be rendered is a priori known (twice
the number of blocks) we devised to use the frag-
ment processor to compute and pack the four end-
points and texture coordinates into two RGBA tex-
tures, each having twice the number of elements as
the number of blocks. One of these textures packs
the endpoints and textures coordinates for the first
(mandatory non wrapping section) line segment and
the other those corresponding to the second (poten-
tially wrapping section) line segment. These textures
are then used as input data for the geometry engine, in
order to create the texturized lines, forwarding them
to the subsequent graphics pipeline. The graphics
hardware clips the lines, generates the fragments with
interpolated texture coordinates, and eventually ren-
der them. As a result, the overall compacted stream is
obtained.
JUMPING JACK - A Parallel Algorithm for Non-Monotonic Stream Compaction
143

True direct RTVA is not directly supported by
OpenGL but it can be achieved using buffer objects .
As in OpenGL these buffer objects are not unified, the
solution comprises rendering into a framebuffer ob-
ject (FBO), then copying the data into a pixel-buffer
object (PBO) and re-casting it as a vertex buffer ob-
ject (VBO). The VBO is then used as geometry input
by a OpenGL call. Copying from the FBO into a PBO
does not involve transfers from GPU to CPU or vice-
versa as it is performed internally and therefore can
be very fast due to the high memory bandwidth of in-
ternal GPU memory.
Other approaches exist as fetching the texture di-
rectly from the vertex processor (VTF), or from the
geometry processor when available (e.g. as suggested
by (Roger et al., 2007)). The latter should enable a
theoretical more optimized process of the wrapping
problem, as the geometry processor has the ability to
generate geometry in a data dependent manner, there-
fore enabling the creation of the second line segment
only when necessary.
6 RESULTS
The intra-block all-prefix-sum computation has no
data dependencies, however it depends on the block
size. We implemented both the double recursive and
the balanced tree approaches. The achieved results
for a 4M element stream (we will use the M prefix
to denote for ×2
20
) are depicted in Figure 9. Results
demonstrate the block-size dependency but the algo-
rithms show opposite behaviors. The recursive dou-
bling algorithm is more efficient for small block sizes,
whereas the balanced tree becomes more efficient as
the block size increases. As a result, the choice for
one algorithm may have consequences on the overall
performance, if not tuned as a function of the block
size.
0
20
40
60
80
100
120
140
1
6
3
2
6
4
1
2
8
2
5
6
5
1
2
1
0
2
4
2
0
4
8
BlockSize
Time(ms)
BalancedTree[Ble90]
RecursiveDoubling[HS86]
Figure 9: Timings achieved for intra-block block prefix-
sums for a stream with 4M elements.
To have a better insight on how the concatenation
varies with the block size, we measured the concate-
nation times for several block sizes. We used a data
set with 50% of invalid elements. Notice that only the
block level compaction component is affected by the
data distribution. Figure 10 presents average timings
to concatenate a 4M stream for block sizes ranging
between 16 and 2048. As expected. the inter-block
sum is faster for greater block sizes. The block-level
compaction is also faster for greater block sizes, how-
ever it appears to revert this behavior for block sizes
above 1024.
0
5
10
15
20
25
30
35
40
16
32
64
128
256
512
1024
2048
BlockSize
Time(ms)
linedrawingusingRTVA
inter‐blockprefix‐sum
Figure 10: Timings for block concatenation for a stream
with 4M elements.
We also observed experimentally, as it was ex-
pectable, that the concatenation process depends on
the number of valid elements. Notice that the work
carried out by the inter-block all-prefix-sum depends
on the number of blocks. Consequently, this data
dependent variation has more impact for large block
sizes, as the all-prefix-sum is faster (reduced number
of blocks) and the number of textured lines is smaller
(less effort by the geometry engine), but the number
of valid elements to render increases (stressing the
rasterizer and texturing units).
We proceed by analyzing the results achieved by
the Jumping Jack Algorithm and compare them with
those achieved by the binary search proposed by Horn
(Horn, 2005). The results herein presented make use
of the block compaction approach. Figure 11 presents
the timings achieved to compact a 4M element stream
against the density of invalid elements (randomly gen-
erated). A block size of 256 was used. Presented time
values correspond to the overall stream compaction
process.
Jumping Jack Algorithm has a stable performance
under densities of 95%, with timings increasing al-
most linearly as the density increases. Above 95%,
there is a significative drop in performance. Notice
that jumping Jack, theoretically, performs the search
process for the number of unpositioned valid ele-
ments. As the invalid densities increases, the proba-
bility of unpositioned elements also increases. On the
other hand, as the invalid densities increase, it also
GRAPP 2009 - International Conference on Computer Graphics Theory and Applications
144
0.00
50.00
100.00
150.00
200.00
250.00
300.00
350.00
0.00 10.00 20.00 30.00 40.00 50.00 60.00 70.00 80.00 90.00 100.00
DensityofInvalidElements(%)
Time(ms)
Horn'sbinarysearch
JumpingJack
Figure 11: Overall time spent for compaction of a 4M
stream by the two tested algorithms, versus the invalid ele-
ments density. A block size of 256 was used.
increases the probability of having imbalanced work
with some elements doing longer searches than oth-
ers. This factor is very noticeable for high densities
of invalid elements.
Horn’s algorithm has a theoretical search com-
plexity, per valid element, that increases with the
number of invalid elements by a factor log
2
(s − v).
As the number of invalid elements increase, the
search complexity increases logarithmically, but the
the search is conducted for less elements. The tim-
ings until densities of 20% are dominated by the log-
arithmic factor, being then dominated by the number
of valid elements, with timings decreasing as the per-
centage of invalids increases.
It can be observed that Jumping Jack algorithm
performs faster than Horn’s for densities under 78%,
demonstrating the practical utility of the algorithm,
when monotonicity is not a requirement, and specifi-
cally when very sparse data is not expectable.
Next, we present the results for the inter-block
compaction process using several block sizes. We
have tested the compaction in two architectures to
conclude about the scalability of the proposed algo-
rithm. Figure 12 shows the achieved timings for the
tested GPU nVidia Go 7300 (3 vertex processors, 4
fragment processors), and Figure 13 for a more recent
nVidia 9500 M GS (NB8P) GPU (with 32 unified pro-
cessors).
The achieved results demonstrate that Jumping
Jack globally maintains its behavior, being faster than
Horn for densities under 70%. A relevant observation
is that, for very sparse data, the Jumping Jack algo-
rithm performs comparatively better with the more re-
cent GPU. In such circumstances, it can be observed
a lesser noticeable drop in performance. This is an
expected result, as the more recent GPU has a better
branch granularity and better loop support.
We observed that speedups ranging between 5×
and 8× were achieved, depending on the algorithm,
block size and data density. A direct comparison can-
0.00
50.00
100.00
150.00
200.00
250.00
300.00
0.00 10.00 20.00 30.00 40.00 50.00 60.00 70.00 80.00 90.00 100.00
DensityofInvalidElements(%)
Time(ms)
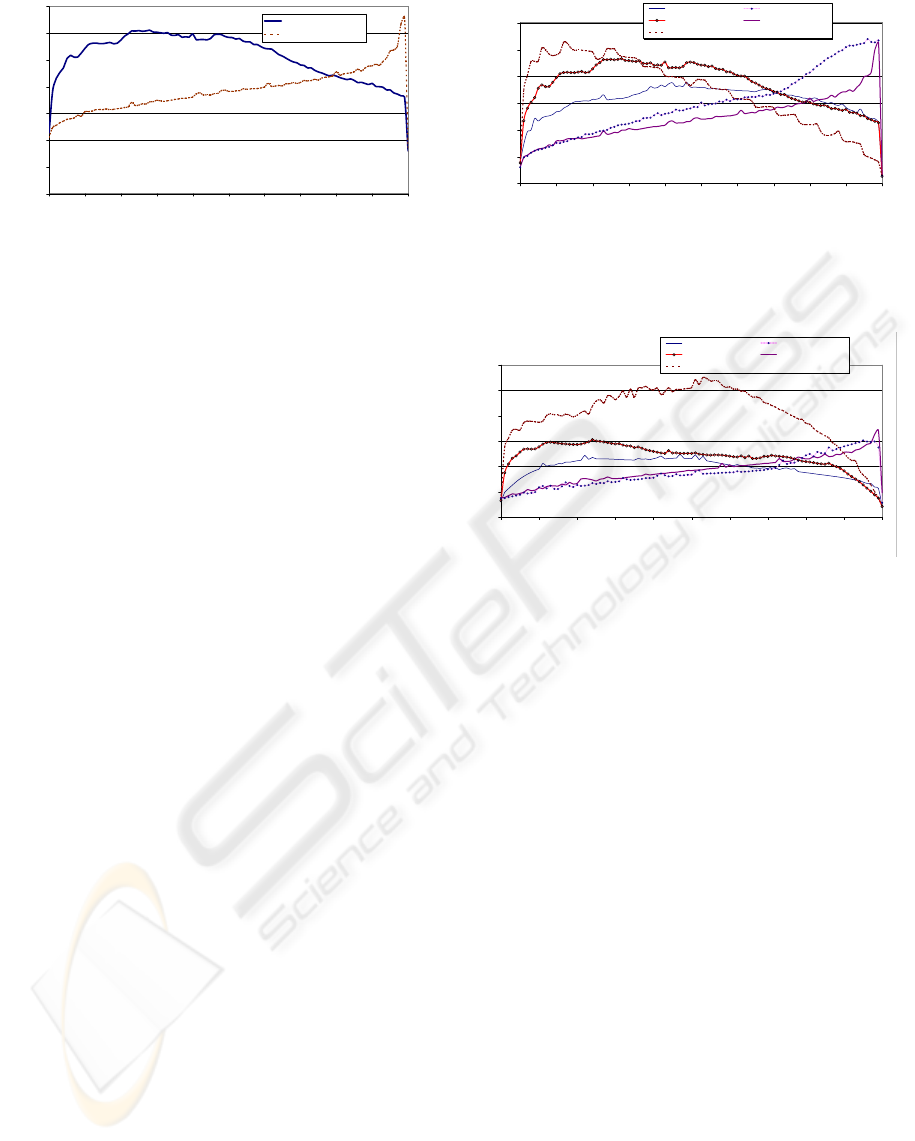
Horn(bs=32) JumpingJack(bs=32)
Horn(bs=256) JumpingJack(bs=256)
Horn(bs=2048)
Figure 12: Timings taken on a nVidia GeForce Go 7300
GPU for intra-block compaction of a 4M stream versus the
invalid elements density (bs denotes the block size).
0
10
20
30
40
50
60
0.00 10.00 20.00 30.00 40.00 50.00 60.00 70.00 80.00 90.00 100.00
DensityofInvalidElements(%)
Time(ms)
Horn(bs=32) JumpingJack(bs=32)
Horn(bs=256) JumpingJack(bs=256)
Horn(bs=2048)
Figure 13: Timings taken on a nVidia GeForce 9500M GPU
for intra-block compaction of a 4M stream versus the in-
valid elements density (bs denotes the block size)
not be easily made as there is no control over the as-
signment of unified processors to each pipeline stage.
Another important observation is that, for the more re-
cent GPU, the algorithms tend to perform better with
smaller block sizes, whereas the older GPU has an op-
posite behavior. Thus, the underlying GPU architec-
ture clearly influences the algorithms performance.
7 CONCLUSIONS AND FUTURE
WORK
This paper introduces Jumping Jack, an original algo-
rithm for non-monotonic stream compaction. To take
full advantage of it, a block based compaction scheme
is proposed. The algorithm is very simple to imple-
ment and has interesting computational complexity
properties. A major weakness of the algorithm rests
in its imbalanced behavior, which is more notably re-
vealed in presence of very sparse data.
The achieved results demonstrate the practical
usefulness of our proposal, for which we pointed
out the advantages and limitations compared to prior
work. We devised strategies and implementation
notes on how to make it useful and demonstrated that
JUMPING JACK - A Parallel Algorithm for Non-Monotonic Stream Compaction
145

the algorithm can perform considerably faster than
existent algorithms.
Our implementations have room to be further op-
timized, as they served fundamentally as a proof of
concept. We plan to continue testing the algorithms
in a broader range of hardware platforms and diversi-
fied data sets, expecting further insights that can lead
to improved variations and ideas. Another avenue to
future work is to study how these algorithms and con-
cepts adapt to the forthcoming (and expectably more
flexible) architectures and standards.
A major conclusion is that performance of com-
paction algorithms may have large data and architec-
tural (inter)dependencies. Tuning an optimal solution,
if possible, is therefore a complex task which is likely
to rely on several variables.
Aware of this, and as a future work avenue, we are
devising solutions that have the ability to adaptively
self-tune in order to achieve a better performance.
This goal is likely to encompass several approaches,
as for instance, developing new algorithms, hybrid al-
gorithms (retaining the best properties of each compo-
nent), and by the use of a generic optimization frame-
work, as outlined in (Moreira et al., 2006), to enable
a dynamic optimization of the compaction process.
ACKNOWLEDGEMENTS
This work has been supported by European Social
Fund program, public contest 1/5.3/PRODEP/2003,
financing request no. 1012.012, medida 5/acção 5.3 -
Formação Avançada de Docentes do Ensino Superior,
submitted by Escola Superior de Tecnologia e Gestão
do Instituto Politécnico de Viana do Castelo.
REFERENCES
Blelloch, G. (1990). Prefix sums and their applications.
Technical Report CMU-CS-90-190, Carnegie Mellon
University - CMU – School of Computer Science,
Pittsburgh, PA 15213.
GPGPU (2008). GPGPU.org. http://www.gpgpu.org.
Greß, A., Guthe, M., and Klein, R. (2006). GPU-based
collision detection for deformable parameterized sur-
faces. Computer Graphics Forum, 25(3):497–506.
Harris, M. (2005). GPU Gems 2, chapter Mapping Compu-
tational Concepts to GPUs, pages 493–508. Addison-
Wesley.
Hensley, J., Scheuermann, T., Coombe, G., Singh, M., and
Lastra, A. (2005). Fast summed-area table genera-
tion and its applications. Computer Graphics Forum,
24(3):547–555.
Hillis, W. D. and Steele JR, G. (1986). Data parallel algo-
rithms. Communications of the ACM, 29(12):1170–
1183.
Horn, D. (2005). GPU Gems 2, chapter Stream reduction
operations for GPGPU applications, pages 573–589.
Addison-Wesley.
Lefohn, A. E., Sengupta, S., and Owens, J. D. (2007). Res-
olution matched shadow maps. ACM Transactions on
Graphics, 26(4):20:1–20:17.
Moreira, P. M., Reis, L. P., and de Sousa, A. A. (2006).
Best multiple-view selection: Application to the visu-
alization of urban rescue simulations. IJSIMM - Int.
Journal of Simulation Modelling, 5(4):167–173.
Nickolls, J., Buck, I., Garland, M., and Skadron, K. (2008).
Scalable parallel programming with CUDA. Queue,
6(2):40–53.
Owens, J. D., Luebke, D., Govindaraju, N., Harris, M.,
Kruger, J., Lefohn, A. E., and Purcell, T. J. (2007).
A survey of general-purpose computation on graphics
hardware. Computer Graphics Forum, 26(1):80–113.
Roger, D., Assarsson, U., and Holzschuch, N. (2007). Whit-
ted ray-tracing for dynamic scenes using a ray-space
hierarchy on the GPU. In Proceedings of the Euro-
graphics Symposium on Rendering’07, pages 99–110.
Sengupta, S., Harris, M., Zhang, Y., and Owens, J. D.
(2007). Scan primitives for GPU computing. In GH
’07: Proceedings of the 22nd Symposium on Graphics
Hardware, pages 97–106.
Sengupta, S., Lefohn, A. E., and Owens, J. D. (2006). A
work-efficient step-efficient prefix sum algorithm. In
Proceedings of the Workshop on Edge Computing Us-
ing New Commodity Architectures, pages D:26–27.
Ziegler, G., Tevs, A., Theobalt, C., and Seidel, H. (2006).
GPU point list generation through histogram pyra-
mids. In 11th Int. Fall Workshop on Vision, Modeling,
and Visualization - VMV’06, pages 137–144.
GRAPP 2009 - International Conference on Computer Graphics Theory and Applications
146
