
IMAGE RETARGETING USING STABLE PATHS
H
´
elder P. Oliveira
Faculdade de Engenharia, Universidade do Porto, Porto, Portugal
Jaime S. Cardoso
INESC Porto, Faculdade de Engenharia, Universidade do Porto, Porto, Portugal
Keywords:
Image processing, Image retargeting, Image resizing, Stable paths.
Abstract:
Media content adaptation is the action of transforming media files to adapt to device capabilities, usually
related to mobile devices that require special handling because of their limited computational power, small
screen size and constrained keyboard functionality. Image retargeting is one of such adaptations, transforming
an image into another with different size. Tools allowing the author to imagery once and automatically retarget
that imagery for a variety of different display devices are therefore of great interest. The performance of these
algorithms is directly related with the preservation of the most important regions and features of the image.
In this work, we introduce an algorithm for automatically retargeting images. We explore and extend a recently
proposed algorithm on the literature. The central contribution is the introduction of the stable paths for image
resizing, improving both the computational performance and the overall quality of the resulting image. The
experimental results confirm the potential of the proposed algorithm.
1 INTRODUCTION
Increasingly, our computing and communications in-
frastructure is evolving to support images and video.
The recent diversity and versatility of mobile dis-
plays, such as PDAs and cellular phones, have en-
larged the importance of adaptation of images for
these devices. Traditional image manipulation tech-
niques, such as scaling and cropping, lead to a degra-
dation of image quality and important loss of informa-
tion when automatically applied to images with mul-
tiple objects. In such techniques, valuable image area
in the target image may be wasted with unimportant
regions between important features. Content aware
retargeting algorithms try to change the image size
while preserving the most important information in
it.
In this work we present a novel scheme to resize
an image. Our algorithm repeatedly carves out multi-
ple lines simultaneously. To do this, we draw on the
work by Avidan and Shamir on seam carving (Avidan
and Shamir, 2007). Analogous to their approach, we
identify low energy seams that are carved out from
the image. The seams are not restricted to be straight
but rather follow the contours of low-gradient regions
in the image. In this work we extend and explore
their approach in two main directions. Firstly, the
use of stable paths instead of the shortest path im-
proves the computational performance of the method
by selecting multiple seams simultaneously. Further-
more, this option also has the advantage of spread-
ing more evenly the removed seams on the image,
improving the overall quality. Secondly, the design
of the weights on the graph resulting from the image
is generalized to depend nonlinearly on the gradient
value. Moreover, we also distinguish, in terms of cost,
pair of pixels 4-neighbourhood-connected from pix-
els only connected under 8-neighbourhoods. This im-
provement in the weight design enhances further the
final performance.
After reviewing the state of the art in image re-
targeting, we introduce in Section 3 the concept of
stable paths in a graph and present a computationally
efficient algorithm for determining them. The exper-
imental work reported at the end of the communica-
tion includes a thorough testing on real images, where
the original method in (Avidan and Shamir, 2007) is
compared with the extensions proposed in this work.
40
P. Oliveira H. and S. Cardoso J. (2009).
IMAGE RETARGETING USING STABLE PATHS.
In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 40-47
DOI: 10.5220/0001785900400047
Copyright
c
SciTePress

2 RELATED WORKS
Before describing in detail the proposed method for
image retargeting it is instructive to examine the cur-
rent state of the art.
A non-photorealistic algorithm was proposed
in (Setlur et al., 2005) to adapt automatically images
for small sized displays with different sizes and/or as-
pect ratios, while preserving the important features in
the image. This is achieved by first decomposing the
image in a background layer and foreground objects.
Then, all important zones are temporally cropped and
the other parts are removed from the image. The fi-
nal image is obtained by pasting the important zones,
with the rest of the image obtained by resizing some
parts using inpainting (Harrison, 2001).
In (Liu and Gleicher, 2005) and (Liu and Gleicher,
2006) the authors propose a method for image and
video retargeting, respectively. Their method presents
a tradeoff between image resizing and image crop-
ping. The method consists on finding the Region-of-
Interest (ROI) of the image and constructing a novel
Fisheye-View warp that applies a linear scaling func-
tion in each dimension of the image. Basically, in this
method the information on the ROI is preserved and
the rest of the image is warped. In the video applica-
tion they use a combination of the image and saliency
maps to find the ROI. After this operation, cropping,
virtual pan and shot cuts are used to resize the image.
In (Gal et al., 2006) is presented a method for in-
homogeneous 2D texture mapping by a feature mask
to the general problem of warping, that preserves
some parts of the image specified by the user. The
feature-aware texture warping is done by applying a
formulation based on Laplacian editing technique.
An automatic non-uniform global warping was
employed by (Wolf et al., 2007) in a problem of video
retargeting. The algorithm starts by analyzing the
frame to detect important zones and then shrinks less
important regions. The analysis of the frames is based
on local saliency, and object and motion detection.
The technique of cropping the important zones
and then resizing them to obtain the desired aspect
ratio was applied in (Tao et al., 2007) to a problem
of video retargeting. In (Chen and Sen, 2008) the au-
thors use graph cuts to find and remove low gradient
sheets, for video summarization applications.
An approach for the summarization of visual data
for images and videos is proposed in (Simakov et al.,
2008). The authors propose a measure to quantify
how “good” is a visual summary. This measure can
be applied to compare two images or two videos se-
quences with different sizes. This is useful to im-
prove some objective function within an optimiza-
tion process, to generate good visual summaries or to
compare quantitatively and evaluate visual summaries
produced by different methods.
An important work in image retrieving was re-
cently presented by Avidan (Avidan and Shamir,
2007), and improved by Rubinstein (Rubinstein et al.,
2008) for video retargeting. In (Avidan and Shamir,
2007) the authors create an operator called seam carv-
ing that permits the reduction and enlarging of im-
ages. A seam was defined as an optimal 8-connected
path of pixels between opposing margins of the im-
age, where optimally is determined using an image
energy function. The algorithm preserves the image
structure by removing more low energy pixels than
high energy pixels. The computation of the optimal
seam is based on an efficient dynamic programming
algorithm. In (Rubinstein et al., 2008) the authors
extend the work for video. There, the dynamic pro-
gramming had to be replaced by graph cuts, suitable
for 3D volumes. A novel energy function was also in-
troduced, improving the visual quality of both videos
and images.
The principal problem of the algorithm in (Avidan
and Shamir, 2007; Rubinstein et al., 2008) is related
with the lower performance when applied to images
with big sizes. The algorithm is slow because only
one line is discarded per iteration.
3 A STABLE PATH APPROACH
FOR IMAGE RESIZING
In the work to be detailed, the image grid is consid-
ered as a graph with pixels as nodes and arcs con-
necting neighbouring pixels. The weight of each arc,
w(p, q), is a function of pixels values and pixels rela-
tive positions. A path from vertex (pixel) v
1
to vertex
(pixel) v
n
is a list of unique vertices v
1
, v
2
, . . . , v
n
, with
v
i
and v
i+1
corresponding to neighbour pixels. The to-
tal cost of a path is the sum of each arc weight in the
path
∑
n
i=2
w(v
i−1
, v
i
).
A path from a source vertex v to a target vertex u
is said to be a shortest path if its total cost is minimum
among all v-to-u paths. The distance between a source
vertex v and a target vertex u on a graph, d(v, u), is the
total cost of a shortest path between v and u.
A path from a sub-graph Ω
1
to a sub-graph Ω
2
is
said to be a shortest path between Ω
1
and Ω
2
if its
total cost is minimum among all v ∈ Ω
1
-to-u ∈ Ω
2
paths. The distance from a sub-graph Ω
1
to a sub-
graph Ω
2
, d(Ω
1
, Ω
2
), is the total cost of a shortest
path between Ω
1
and Ω
2
:
d(Ω
1
, Ω
2
) = min
v∈Ω
1
,u∈Ω
2
d(v, u). (1)
IMAGE RETARGETING USING STABLE PATHS
41

3.1 Algorithm Outline
For completeness and to help introducing the pro-
posed method, we summarize here the method
in (Avidan and Shamir, 2007), in which we build on.
The presentation will rely on height reduction only;
the necessary adaptations for width reduction or im-
age enlarging should be clear at the end.
To reduce the height of an image by one pixel,
one needs to remove one and only one pixel in each
column. Moreover, in order to prevent discontinuities,
the removed pixels should be connected. Therefore,
we are allowed to remove only any connected path
from the left to the right margins, without zig zagging
back and forth (Avidan and Shamir, 2007). Formally,
let I be an N
1
×N
2
image and define an admissible
path to be
s = {(x, y(x))}
N
1
x=1
, s.t. ∀x |y(x) −y(x −1)|≤ 1,
where y is a mapping y : [1, ··· , N
1
] → [1, ··· , N
2
].
That is, an admissible path is an 8-connected path of
pixels in the image from left to right, containing one,
and only one, pixel in each column of the image.
In (Avidan and Shamir, 2007) the authors propose
to remove the path with least energy. Toward that
end a weight (= energy) is defined for each arc con-
necting neighbour pixels; then the optimal path is the
minimum-cost path connecting the two lateral mar-
gins. This optimal path can be found using dynamic
programming. The first step is to traverse the image
from the second column to the last column and com-
pute the cumulative minimum cost C for all possible
connected staff lines for each entry (i, j):
C(i, j) = min
C(i −1, j −1) + w(p
i−1, j−1
; p
i, j
)
C(i −1, j) + w(p
i−1, j
; p
i, j
)
C(i −1, j + 1) + w(p
i−1, j+1
; p
i, j
)
,
where w(p
i, j
; p
l,m
) represents the weight of the edge
incident with pixels at positions (i, j) and (l, m). At
the end of this process,
min
j∈{1,···,N
2
}
C(N
1
, j)
indicates the end of the minimal connected path.
Hence, in the second step, one backtrack from this
minimum entry on C to find the path of the optimal
staff.
3.1.1 Design of the Weight Function
It is important to call the attention for the first im-
provement over (Avidan and Shamir, 2007). In (Avi-
dan and Shamir, 2007), the authors define a weight
(energy) on each pixel. In here we put the weight
on the arc connecting two neighbour pixels. Had we
defined the arc’s weight as the average of the pixels’
weight, our formulation would resume to the previ-
ous. But by putting the weight on the arc we have
now the flexibility to distinguish a path over an arc
connecting 4-neighbour pixels from an arc connect-
ing 8-neighbour pixels, penalising the latter over the
former. The weight of each arc is a function of pixels
values and pixels relative positions.
In this work we set
w(p
i, j
; p
l,m
) =
f (p
i, j
, p
l,m
)
if p
i, j
, p
l,m
are 4-neighbours
√
2 f (p
i, j
, p
l,m
)
if p
i, j
, p
l,m
are 8-neighbours
Note that is important to set f (p
i, j
, p
l,m
) strictly
greater than zero so that
√
2 f (p
i, j
, p
l,m
) is strictly
greater than f (p
i, j
, p
l,m
).
3.2 Stable Paths on a Graph
1
Assume one wants to decrease the height of the image
by several pixels. This can be approached by succes-
sively finding and removing the shortest path from the
left to the right margin of the image. A preferable so-
lution would be to find multiple paths in a single itera-
tion. The stable path method allows us to do precisely
that.
Before moving to the formal definition of a stable
path on a graph, it is instructive to motivate the con-
cept by considering a hypothetical, simplified 9 ×10
image. The graph corresponding to such image is rep-
resented in Figure 1. The design of the weight func-
tion will be considered next; for now, it suffices to
know that black pixels represent pixels with low cost
(energy), likely resulting from points with low gradi-
ent.
The shortest path between the left and right mar-
gins (sub-graphs Ω
1
and Ω
2
) is the path correspond-
ing to the fourth row, entirely through black pixels.
By following the strategy just delineated, one could
reduce the height by four pixels in four iterations, se-
quentially. Nonetheless, although only one path cor-
responds to the shortest path, it is visible multiple ‘al-
most optimal’ paths. The stable path concept provides
a means to find all of such paths simultaneously.
Definition. A path P
s,t
is a stable path between re-
gions Ω
1
and Ω
2
if P
s,t
is the shortest path between
s ∈ Ω
1
and the whole region Ω
2
, and P
s,t
is the short-
est path between t ∈Ω
2
and the whole region Ω
1
.
1
A first incursion into stable paths is already present
in (Cardoso et al., 2008), in the context of medical imag-
ing; here we provide, arguably, a cleaner presentation.
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
42

Figure 1: Stable paths on a toy example.
Note that the concept of stable path is valid for
any graph and any two sub-graphs in general. The
computation of the stable paths on the toy example of
Figure 1 provides the three paths gray-highlighted in
the figure.
In Figure 2(b) the shortest paths between each
point on the left margin and the whole right margin
are traced. Likewise, Figure 2(c) shows the shortest
paths between each point on the right margin and the
whole left margin. The set of stable paths between
both margins result as the set of paths present in both
figures, as illustrated in Figure 2(d).
Although the computation of the stable paths may
be expensive in general graphs, the computation in
the graph derived from an image under the setting
adopted in Section 3.1 has only roughly twice the
complexity of the shortest path computation pre-
sented in the same Section. Noticing that the proce-
dure delineated in Section 3.1 actually gives the short-
est path between the whole left margin Ω
1
and each
point on the right margin Ω
2
, the first step on the com-
putation of the stable path corresponds verbatim to
the computation of the shortest path presented on Sec-
tion 3.1. In a second step one repeats the same proce-
dure, traversing now the graph from the right column
to the left. At the end of this process, if the two end-
points of a direct and reverse path coincide, we are in
the presence of a stable path.
Noticing that the two steps of computing the short-
est paths in both directions can done in parallel and
most personal computers are nowadays dual cores, the
computation of the stable paths takes essentially the
same time as the shortest path computation. Finally,
when the number of stable paths is less than the num-
ber of lines to be removed, one just repeats the proce-
dure after removing the stable paths found; when the
number of stable paths is larger than the necessary,
one just keeps the shortest stable paths. While the de-
scription has focused on height reduction, the same
mechanism applies for width reduction or image en-
(a) Original image. (b) Shortest paths from each
pixel in the left column and
the whole right column, su-
perimposed on the original
image.
(c) Shortest paths from each
pixel in the right column and
the whole left column, super-
imposed on the original im-
age.
(d) Resulting stable paths.
Figure 2: Exemplification of stable paths for Figure 2(a).
(a) Original image. (b) Original image stable
paths superimposed.
Figure 3: Staff lines for Figure 3(a).
larging, totally in line with the adaptations in (Avidan
and Shamir, 2007).
Summing up, two main advantages accrue from
IMAGE RETARGETING USING STABLE PATHS
43

the replacement of the sequential search of the short-
est path by the search of stable paths: multiple lines
can be computed in a single iteration, saving on the
computational time; the stable path approach tends to
spread the lines over the image, as observed in Fig-
ure 2 and Figure 3.
Indeed, while the shortest paths tend to be all clus-
tered in a single, gradient-free zone of the image, the
stable paths are usually found in several zones of the
image.
4 RESULTS
The proposed methodology was applied to a set of 36
images. Only the luminance information was used in
the analysis. The weight of an arc is based on the
energy of the incident pixels. Like in (Avidan and
Shamir, 2007), the energy function is derived from
the gradient information. Our gradient model is based
on the Sobel operator. The Sobel operator is applied
on the x and y directions; from the computed values,
E
x
and E
y
, the magnitude of the gradient is estimated
as E =
q
E
2
x
+ E
2
y
, as exemplified in Figure 4. Al-
though more general setting could have been adopted,
we fixed the weight of an arc as monotonically in-
creasing function of the average energy of the inci-
dent pixels (or
√
2 times that value, for 8-neighbour
pixels): f (p
i, j
, p
l,m
) =
ˆ
f (
E
i, j
+E
l,m
2
) .
(a) Original image. (b) Gradient image.
Figure 4: Gradient based on the Sobel operator.
Weights were assigned based on an power law:
ˆ
f (E) = δ + 255
E
255
n
, δ, n ∈ ℜ
The parameters δ and n were experimentally tuned,
yielding δ = 32 and n = 2. For comparison purposes
(a) Original image. (b) Resized image using the
linear shortest path method.
(c) Resized image using the
linear stable path method.
(d) Resized image using the
nonlinear stable path method.
Figure 5: Results of the different resizing methods when
applied to image E.
we also evaluated the linear weight (n = 1). Five dif-
ferent methods are experimentally compared:
1. Linear Shortest Path. A slightly improved ver-
sion of the method in (Avidan and Shamir, 2007),
with the incorporation of the δ > 0 parameter, to
ensure that the cost of 8-neighbour pixels is larger
than 4-neighbour pixels. This method discards a
single line per iteration.
2. Linear Stable Path. Based on stable paths to dis-
card multiple line per iteration but using the linear
weight function (n = 1).
3. Nonlinear Shortest Path The method of (Avidan
and Shamir, 2007) discarding a single line per it-
eration but using the nonlinear weight function
(n = 2).
4. Nonlinear Stable Path. Based on stable paths to
discard multiple line per iteration and using the
nonlinear weight function (n = 2).
5. Scaling. Standard scaling, with Lanczos filtering.
The new size of each image was subjectively cho-
sen to make visible differences between the different
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
44
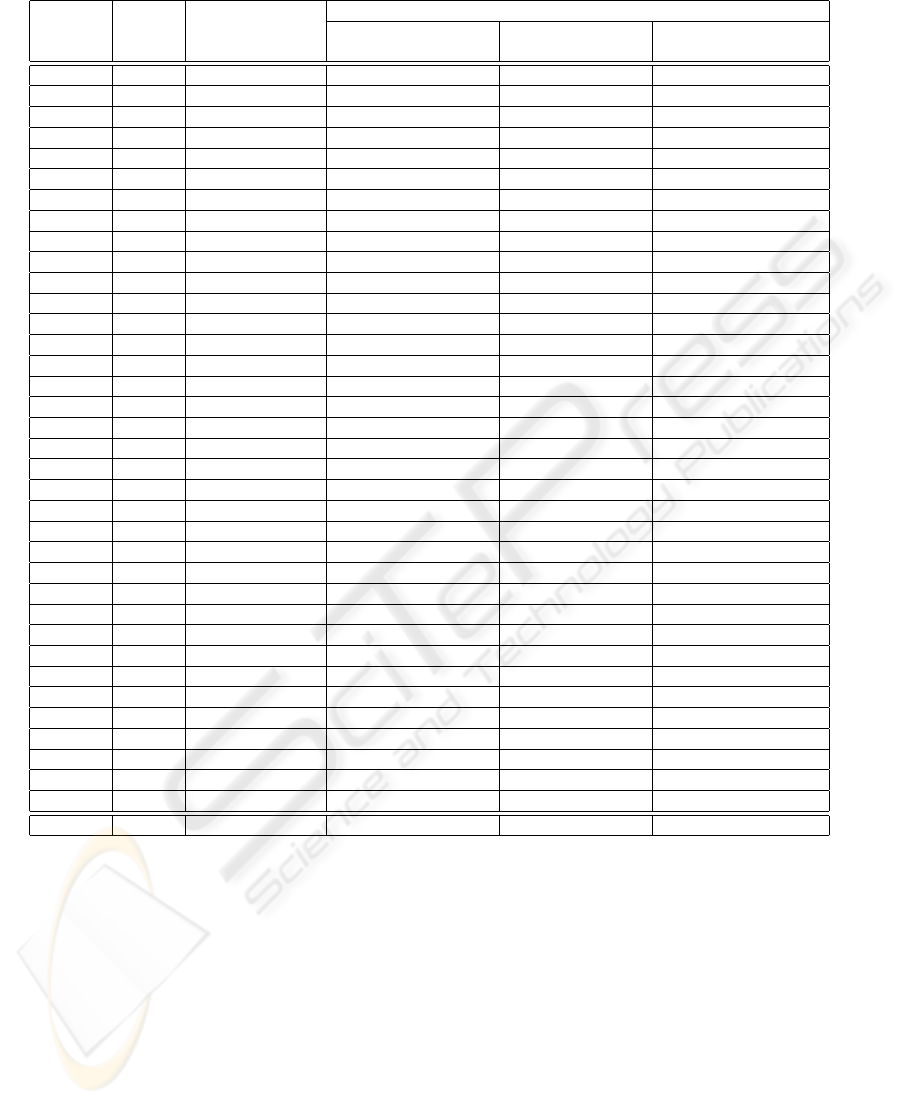
Table 1: Results obtained using different resize methods.
Image Height Discarded Lines
Number Iterations
Linear and nonlinear
Linear stable path Nonlinear stable path
shortest path
A 230 35 35 20 (57%) 12 (34%)
B 230 35 35 14 (40%) 5 (14%)
C 288 80 80 42 (53%) 42 (53%)
D 230 10 10 10 (100%) 6 (60%)
E 300 80 80 58 (73%) 49 (61%)
F 200 30 30 21 (70%) 13 (43%)
G 300 60 60 26 (43%) 25 (42%)
H 300 75 75 44 (59%) 41 (55%)
I 230 80 80 51 (64%) 53 (66%)
J 230 110 110 75 (68%) 61 (55%)
K 230 60 60 30 (50%) 34 (57%)
L 180 60 60 37 (62%) 29 (48%)
M 220 60 60 27 (45%) 16 (27%)
N 1536 150 150 46 (31%) 6 (4%)
O 1944 100 100 29 (29%) 15 (15%)
P 800 100 100 48 (48%) 14 (14%)
Q 600 70 70 34 (49%) 30 (43%)
R 800 90 90 33 (37%) 27 (30%)
S 355 80 80 58 (73%) 10 (13%)
T 274 70 70 43 (61%) 38 (54%)
U 400 100 100 41 (41%) 36 (36%)
V 402 70 70 31 (44%) 23 (33%)
W 290 30 30 10 (33%) 4 (13%)
X 375 30 30 29 (97%) 27 (90%)
Y 504 70 70 32 (46%) 21 (30%)
Z 411 130 130 59 (45%) 56 (43%)
AA 332 35 35 18 (51%) 22 (63%)
AB 350 110 110 60 (55%) 63 (57%)
AC 375 50 50 31 (62%) 25 (50%)
AD 385 50 50 27 (54%) 14 (28%)
AE 300 65 65 30 (46%) 33 (51%)
AF 480 50 50 20 (40%) 19 (38%)
AG 324 40 40 36 (90%) 23 (58%)
AH 504 150 150 24 (16%) 15 (10%)
AI 319 150 150 57 (38%) 8 (5%)
AJ 428 150 150 38 (25%) 27 (18%)
Average (53%) (39%)
methods. The results can be found in the Table 1. The
percentage values are the fraction of iterations neces-
sary by the stable path algorithms relative to the to-
tal number of iteration required by the shortest path
methods (that matches the number of removed lines).
It can be observed that the proposed algorithm has
a very interesting performance. The use of the stable
paths reduced the number of iterations and the corre-
sponding computational complexity. The simultane-
ous use of a nonlinear weight function and the stable
path method reduced further the number of iterations
required to resize the image.
In a second experiment we evaluated the impact
on quality of the use of stable paths to resize images.
It is important to confirm if we are trading off quality
for computational performance.
In Figures 5 and 6 it is presented the results ob-
tained with the linear shortest path method and the
linear and nonlinear stable path method. It is possible
to observe that the stable path method attain a better
quality; the principal visual improvement can be seen
on people appearance.
From the analysis of the results reported in Fig-
ure 7, it is possible to conclude that the nonlinear
weight function presents a better behaviour than the
linear weight. The principal visual impact can be seen
on the horizon of the scenery. Furthermore, is pos-
sible to observe, by comparing Figure 7(c) and 7(d),
that the stable path algorithm outperforms the shortest
path algorithm. The resized image using our method
IMAGE RETARGETING USING STABLE PATHS
45

(a) Original image. (b) Resized image using the
linear shortest path method.
(c) Resized image using the
linear stable path method.
(d) Resized image using
the nonlinear stable path
method.
Figure 6: Results of the different resizing methods when
applied to image V.
(a) Original image. (b) Resized image using the
linear shortest path method.
(c) Resized image using
the nonlinear shortest path
method.
(d) Resized image using the
nonlinear stable path method.
Figure 7: Results of the different resizing methods when
applied to image J.
seems more natural: in Figure 7(c) the sky is very
compacted when compared with Figure 7(d).
In Figures 8 and 9 we can observe that our al-
gorithm can be simultaneously faster and with better
quality than the version in (Avidan and Shamir, 2007),
both on small sized images and big sizes image, re-
spectively.
(a) Original image. (b) Resized image using the
linear shortest path method.
(c) Resized image using
the nonlinear shortest path
method.
(d) Resized image using the
nonlinear stable path method.
Figure 8: Results of the different resizing methods when
applied to image AI.
(a) Original image. (b) Resized image using the
linear shortest path method.
(c) Resized image using
the nonlinear shortest path
method.
(d) Resized image using the
nonlinear stable path method.
Figure 9: Results of the different resizing methods when
applied to image N.
The lack of metrics to perform this evaluation ob-
jectively, led us to create a panel of observers to evalu-
ate subjectively the output of the different algorithms.
Besides confirming the results already demonstrated,
an interesting conclusion was that, in some images,
the traditional rescaling continues to be preferable.
5 CONCLUSIONS
We presented an algorithm for content-aware image
resizing. The proposed method is an improvement
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
46

over an already established method in the literature.
We exploit the concept of stable paths to enhance both
the computational speed and the quality of the result-
ing image. The generalization of the weight function
of the graph derived from the image further improved
the quality results. Though the experimental results
have focused on image reduction only, the method is
straightforwardly applied to image enlarging, image
amplification and object removal. We intend now to
generalize and adapt the concept of stable paths for
video retargeting.
REFERENCES
Avidan, S. and Shamir, A. (2007). Seam carving for
content-aware image resizing. ACM Trans. Graph.,
26(3):10.
Cardoso, J. S., Teixeira, L. F., and Cardoso, M. J. (2008).
Automatic breast contour detection in digital pho-
tographs. In Proceedings of the International Con-
ference on Health Informatics (HEALTHINF 2008),
volume 2, pages 91–98.
Chen, B. and Sen, P. (2008). Video carving. In Short Papers
Proceedings of Eurographics.
Gal, R., Sorkine, O., and Cohen-Or, D. (2006). Feature-
aware texturing. In Proceedings of Eurographics Sym-
posium on Rendering, pages 297–303.
Harrison, P. (2001). A non-hierarchical procedure for re-
synthesis of complex textures. In WSCG 2001 Con-
ference proceedings, pages 190–197. WSCG.
Liu, F. and Gleicher, M. (2005). Automatic image retarget-
ing with fisheye-view warping. In UIST ’05: Proceed-
ings of the 18th annual ACM symposium on User in-
terface software and technology, pages 153–162, New
York, NY, USA. ACM.
Liu, F. and Gleicher, M. (2006). Video retargeting: au-
tomating pan and scan. In MULTIMEDIA ’06: Pro-
ceedings of the 14th annual ACM international con-
ference on Multimedia, pages 241–250, New York,
NY, USA. ACM.
Rubinstein, M., Shamir, A., and Avidan, S. (2008). Im-
proved seam carving for video retargeting. ACM
Transactions on Graphics (SIGGRAPH), 27(3).
Setlur, V., Takagi, S., Raskar, R., Gleicher, M., and Gooch,
B. (2005). Automatic image retargeting. In MUM
’05: Proceedings of the 4th international conference
on Mobile and ubiquitous multimedia, pages 59–68,
New York, NY, USA. ACM.
Simakov, D., Caspi, Y., Shechtman, E., and Irani, M.
(2008). Summarizing visual data using bidirectional
similarity. In IEEE Conference on Computer Vision
and Pattern Recognition, pages 1–8.
Tao, C., Jia, J., and Sun, H. (2007). Active window ori-
ented dynamic video retargeting. In Proceedings of
the Workshop on Dynamical Vision.
Wolf, L., Guttmann, M., and Cohen-Or, D. (2007). Non-
homogeneous content-driven video-retargeting. In
IEEE 11th International Conference on Computer Vi-
sion, pages 1–6.
IMAGE RETARGETING USING STABLE PATHS
47
