
SOLVING ILL-POSED PROBLEMS USING DATA ASSIMILATION
Application to Optical Flow Estimation
Dominique B´er´eziat
Universit´e Pierre et Marie Curie, LIP6, 4 place Jussieu, 75005 Paris, France
Isabelle Herlin
INRIA, CEREA, Joint Laboratory ENPC-EDF R&D, Universit´e Paris-Est
BP105 78153 Le Chesnay Cedex, France
Keywords:
Data Assimilation, Ill-posed Problem, Variational Formulation, Optical Flow, Missing Data.
Abstract: Data Assimilation is a mathematical framework used in environmental sciences to improve forecasts per-
formed by meteorological, oceanographic or air quality simulation models. Data Assimilation techniques
require the resolution of a system with three components: one describing the temporal evolution of a state
vector, one coupling the observations and the state vector, and one defining the initial condition. In this article,
we use this framework to study a class of ill-posed Image Processing problems, usually solved by spatial and
temporal regularization techniques. A generic approach is defined to convert an ill-posed Image Processing
problem in terms of a Data Assimilation system. This method is illustrated on the determination of optical
flow from a sequence of images. The resulting software has two advantages: a quality criterion on input data
is used for weighting their contribution in the computation of the solution and a dynamic model is proposed
to ensure a significant temporal regularity on the solution.
1 INTRODUCTION
In the research field of Image Processing, most prob-
lems are ill-posed in the sense that it is not possible to
provide a unique solution (Hadamard, 1923). A com-
mon cause of ill-posedness is that the equations used
to model image properties, called Image Model, are
under-determined. An example is the famous “aper-
ture problem” occurring in the estimation of optical
flow.
A possible strategy to solve ill-posed problems is
to provide the Image Model with additional informa-
tion. Two options are considered: 1) Providing ex-
plicit information: additional images are used to en-
large the set of input data. However, this is generally
not possible because other acquisitions having the re-
quested properties are often not available. 2) Provid-
ing implicit information: either hypotheses on image
properties or constraints on the solution can be used.
A usual constraint is to restrict the dimension or the
size of the space of admissible solutions: for instance
the result is searched among the functions having
bounded spatial variations (Tikhonov, 1963). Such
methods are called “Tikhonov regularization meth-
ods”. In the general case, these additional image
properties and constraints are expressed as equations,
which, added to the Image Model, lead to a new in-
vertible model.
Assuming an image sequence is available, the
Tikhonov regularization can be extended by consid-
ering a regularization acting both in spatial and tem-
poral domains. This has been proposed by Weick-
ert (Weickert and Schn¨orr, 2001) for determining op-
tical flow. The interest is to produce a solution which
is regular in time and in space. This approach has
however several drawbacks. First, the temporal regu-
larization imposes an arbitrary regularity which can
not deal with complex dynamics. Second, if irrele-
vant input data values occur on large regions, they are
however taken into account in the estimation process
and introduce errors in the solution. These aberrant
values may be due to a sensor failure or an acquisi-
tion noise. We call them “missing data” in the remain
of this paper. Third, as the solution is looked for in the
spatio-temporal domain, this leads to a high complex-
ity in comparison with a pure spatial model, which is
a limiting factor for operational purposes.
An alternative to the Weickert’s approach is to
model the temporal evolution of images. Such a mod-
elling can be inferred, for instance, from a priori
595
Béréziat D. and Herlin I. (2009).
SOLVING ILL-POSED PROBLEMS USING DATA ASSIMILATION - Application to Optical Flow Estimation.
In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 595-602
DOI: 10.5220/0001792205950602
Copyright
c
SciTePress
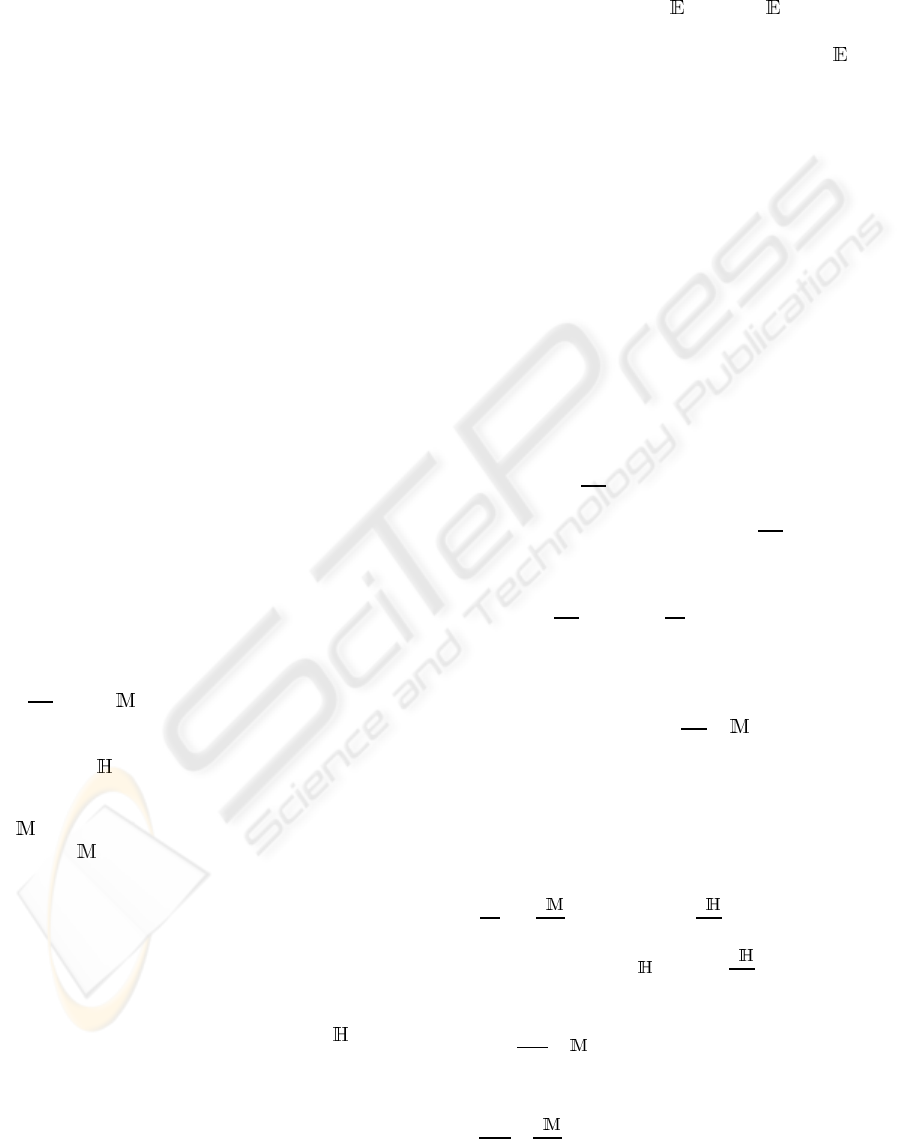
knowledge on image acquisition. The challenge be-
comes to define an effective and pertinent model, and
to include it in the solution computation. Data qual-
ity has also to be evaluated in order to ignore missing
data.
In this paper, we propose to use the Data Assimi-
lation framework as a generic tool to solve ill-posed
problems in Image Processing. A Data Assimilation
method solves simultaneously an evolution equation,
describing the evolution of a state vector over time,
and an observation equation, modelling the links be-
tween the state vector and the observations. Each
equation can be inaccurate and a description of the
errors is stated in terms of a Gaussian noise charac-
terized by a covariance matrix. As it will be shown
in the paper, Data Assimilation is a suitable approach
to solve the three drawbacks of Weickert’s methods
because: the evolution model describes the images’
temporal dynamics; the covariance associated to the
observation equation error overcomes the problem of
missing data by weighting, at each pixel, the contribu-
tion of the observation equation in the computation of
the solution; Data Assimilation is a frame-by-frame
process allowing an affordable computational cost.
2 THE DATA ASSIMILATION
FRAMEWORK
The Data Assimilation framework aims to solve the
system (1,2,3) with respect to a state vector X(x,t),
depending on the spatial coordinate x and time t:
∂X
∂t
(x, t) + (X)(x,t) = ε
m
(x, t) (1)
X(x, 0) = X
b
(x) + ε
b
(x) (2)
(Y, X)(x,t) = ε
O
(x, t) (3)
Equation (1) describes the temporal evolution of
X. , called evolution model, is supposed differen-
tiable. As approximately describes the evolution
of the state vector, a model error ε
m
is introduced to
quantify inaccuracies. Equation (2) establishes the
initial condition of the state vector and the error is
expressed by the background error ε
b
. Equation (3),
called observation equation, describes the links, pos-
sibly complex and non-linear, between the observa-
tion vector, Y(x, t), and the state vector. The observa-
tion error ε
O
represents the imperfection of and the
measurement errors. ε
m
, ε
b
and ε
O
are assumed to be
Gaussian and fully characterized by their covariance
matrices Q, B and R.
Let X denote a Gaussian stochastic vector depend-
ing on a space-time coordinate (x, t). X = X(x, t) and
X
′
= X(x
′
,t
′
) are the values on two locations. The co-
variance matrix Σ, computed for X and X
′
, measures
their dependency and is defined by:
Σ(x,t, x
′
,t
′
) =
ZZ
(X − X)
T
(X
′
− X
′
)dP
X,X
′
P
X,X
′
is the joint distribution of (X, X
′
) and de-
notes the expectation. P
X,X
′
is a Gaussian distribu-
tion whose covariance matrix depends on x, t, x
′
and
t
′
. The inverse of a covariance matrix is formally and
implicitly defined (Oliver, 1998) by:
ZZ
Σ
−1
(x, t, x
′′
,t
′′
)Σ(x
′′
,t
′′
, x
′
,t
′
)dx
′′
dt
′′
=
δ(x− x
′
)δ(t −t
′
) (4)
with δ denoting the Dirac function.
We note A = Ω × [0, T], Ω being the spatial do-
main and [0, T] the temporal domain. In order to solve
equations (1), (2) and (3), we define the functional E,
to be minimized, as stated by equation (5), displayed
at the top of next page. If ε
m
, ε
b
and ε
O
are assumed
to be independent, E represents the log-likelihood of
X. The minimization is carried out using a calcu-
lus of variations: the differential of E with respect
to X, denoted
∂E
∂X
, is calculated and the associated
Euler-Lagrange equation is solved.
∂E
∂X
is obtained
by (i) computing the derivative of E in the direction
η:
∂E
∂X
(η) = lim
γ→0
d
dγ
(E(X+ γη)) (6)
(ii) introducing an auxiliary variable λ, called adjoint
variable in the literature:
λ(x, t) =
Z
A
Q
−1
(x, t, x
′
,t)
∂X
∂t
+ (X)
(x
′
,t
′
)dx
′
dt
(7)
and (iii) writing the state vector X as X
b
+δX. Vectors
X
b
and δX are respectively called background vector
and incremental vector in the Data Assimilation liter-
ature. This leads to the following system of equations:
λ(x, T) = 0 (8)
−
∂λ
∂t
+
∂
∂X
X
b
∗
λ = −
Z
A
∂
∂X
X
b
∗
R
−1
(9)
(X
b
, Y) +
∂
∂X
X
b
(δX)
dx
′
dt
′
X
b
(x, 0) = X
b
(x) (10)
∂X
b
∂t
+ (X
b
) = 0 (11)
δX(x, 0) =
Z
Ω
Bλ(x
′
, 0)dx
′
(12)
∂δX
∂t
+
∂
∂X
X
b
(δX) =
Z
A
Qλ(x
′
,t
′
)dx
′
dt
′
(13)
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
596

E(X) =
Z
A
Z
A
∂X
∂t
+ (X)
T
(x, t)Q
−1
(x, t, x
′
,t
′
)
∂X
∂t
+ (X)
(x
′
,t
′
)dxdtdx
′
dt
′
+
Z
A
Z
A
(X, Y)
T
(x, t)R
−1
(x, t, x
′
,t
′
) (X, Y)(x
′
,t
′
)dxdtdx
′
dt
′
+
Z
Ω
Z
Ω
X(x, 0) − X
b
(x)
T
B
−1
(x, x
′
)
X(x
′
, 0) − X
b
(x
′
)
dxdx
′
(5)
The reader is referred to (Valur H´olm, 2003) for de-
tails on the determination of the differential of E and
Euler-Lagrange equations. The decomposition of the
state vector into background and incremental vectors
requires linearizing the operators and using a
first-order Taylor development: (X) ≃ (X
b
) +
∂
∂X
X
b
(δX). The operator
∂·
∂X
∗
is called adjoint
operator and represents a compact notation for inte-
gration by parts of the differential of the operators
and . It is formally defined by:
∂
∂X
(η), λ
=
η,
∂
∂X
∗
(λ)
(14)
Riesz’s theorem ensures the existence and unique-
ness of the adjoint operator. To solve the system (8)
to (13), equation (11) is first solved using initial con-
dition (10) and provides X
b
. Equation (9) is solved
retrogradely to provide λ using initial condition (8).
The incremental vector is finally provided by solv-
ing (13) with (12) as initial condition. If and
are not linear, an iterative algorithm is used to sequen-
tially improve the solution of (8,9,12,13): at each iter-
ation, the value δX is computed from the background
vector X
b
and the value δX+ X
b
becomes the back-
ground vector for the next iteration.
3 IMAGE ASSIMILATION
This section explains how to solve ill-posed Image
Processing problems using the framework of Data
Assimilation and constitutes the core of the research
and the main contribution of the paper. Using Data
Assimilation to solve Image Processing Problem is
an emerging domain. Studies have been done about
curve tracking (Papadakis and M´emin, 2007) and de-
termination of optical flow (Papadakis et al., 2007a;
Papadakis et al., 2007b). In (Huot et al., 2008), a
method is proposed to estimate the ocean surface cir-
culation from SST images by assimilating image data
in an image model for producing pseudo-observations
for the oceanographic model. In this paper, we con-
sider the general case of ill-posed problems, solved
using Tikhonov regularization methods, and we de-
fine a method to convert them, in a generic way, from
Tikhonov regularization to Data Assimilation frame-
work.
First, state and observation vectors have to be de-
fined. Obviously, the observations will be images or
processed images, and the content of the state vector
will strongly depends on the studied application. For
example, segmentation, denoising and restoration use
a state vector which is an image. Tracking, image reg-
istration and motion estimation are represented by a
vector field. Active contours are modelled by curves.
Sometimes, the links between the state vector and the
observation are highly indirect. For instance, as it is
not possible to deduce the ocean circulation from sur-
face temperatures by a shallow-water model, an addi-
tional system has to be considered with relevant evo-
lution and observation equations (Huot et al., 2008).
To solve an Image Processing problem with the
4D-Var algorithm, as described in Section 2, a suit-
able evolution model describing the temporal evolu-
tion of the state vector has to be stated. Its associated
error must also be defined. Next, an observation equa-
tion and its error should characterize the properties of
observations. Last, the initial condition and its back-
ground error have to be established. This is discussed
in the next Subsections.
3.1 The Evolution Model and Error
One first choice of evolution model is to consider the
simple transport equation
dX
dt
= 0, or:
∂X
∂t
+
∂X
∂x
∂x
∂t
= 0 (15)
The evolution model is then obtained by identifica-
tion: (X)(x,t) =
∂X
∂x
∂x
∂t
. Section 4 describes the
use of equation (15) for determining optical flow.
Another possible choice is to express the transport
of the state vector as a diffusion, a physical law rul-
ing the transport of chemical species or temperature.
The general formulation is:
∂X
∂t
= ∇
T
(D∇X) with
∇ =
∂
∂x
,
∂
∂y
T
. D is a tensor characterizing the di-
rection and intensity of the diffusion. It is possible to
drive this diffusion according to the image character-
istics. A well-known example is the Perona & Malik
diffusion: the tensor matrix is equal to c(k ∇Xk)Id
with c a Gaussian function and Id the identity matrix.
SOLVING ILL-POSED PROBLEMS USING DATA ASSIMILATION - Application to Optical Flow Estimation
597

One property of this diffusion is to smooth the image
while preserving the contours. In this case, identifica-
tion gives: (X) = − ∇
T
(D∇X).
The matrix Q of the model error ε
m
has to be spec-
ified. It is first important to understand the action of
Q
−1
in the functional (5). Let us describe two possi-
ble choices for Q and analyze their impact in a func-
tional E(X) =
RR
F
T
(X)Q
−1
F(X)dxdx
′
which has to
be minimized.
First, let Q being the Dirac covariance defined
by Q(x, x
′
) = δ
x− x
′
. We have E(X) =
R
Ω
kF(X)k
2
dx: a Dirac covariance is corresponding
to a zero-order regularization.
A second choice is the exponential covariance de-
fined by Q(x, x
′
) = exp
−
x− x
′
σ
. We have E(X) =
1
2σ
Z
kF(X)k
2
+ σ
2
∂F(X)
∂x
2
!
dx. The expo-
nential covariance is associated to a first-order reg-
ularization.
In the general case, the inversion of a covariance ma-
trix is often non-trivial and usually inaccessible. Re-
strictive choices have to be made such as the previ-
ous ones. For further details, the reader is referred
to (Oliver, 1998; Tarantola, 2005; B´er´eziat and Her-
lin, 2008).
3.2 The Observation Equation and
Error
As previously pointed out in Section 2, the observa-
tion equation describes the links between the state
vector and the observations. As the regularization
part of the Tikhonov’s method does not contain ob-
servation values, the observation equation will be ex-
actly corresponding to the Image Model existing in
the Tikhonov’s approach.
The observation error has to be stated and its co-
variance matrix R specified. R has then to be inverted
(see equation (9)) and, as explained, this is only pos-
sible for simple cases. The Dirac covariance can be
used to express a null interaction between two space-
time locations. This allows observation errors to be
located and quantified in space and time. R is written
as:
R(x, t, x
′
,t
′
) = r(x, t)δ
x− x
′
δ
t − t
′
(16)
with r a real invertible matrix and:
R
−1
(x, t, x
′
,t
′
) = δ
x− x
′
δ
t − t
′
r
−1
(x, t) (17)
The matrix r
−1
characterizes the quality of the ob-
servation: a high value indicates that the observa-
tion is relevant. Assuming the availability of a func-
tion f measuring the confidence in observation values
(f ∈ [0, 1], f = 0 for no confidence), r
−1
can be de-
fined by:
r
−1
(x, t) = r
0
(1− f(x, t) + r
1
f(x, t) (18)
r
−1
(x, t) will be close to a “minimal value” r
0
on re-
gions where confidence is low and r
1
otherwise. r
0
and r
1
are constant and invertible matrices. For effi-
ciency, f is modeled as:
f(x, t) = f
noise
(x, t) f
sensor
(x, t) f (x,t) (19)
f
noise
characterizes noise acquisition: it is close to 0
for large noise. f
sensor
is equal to 0 when data are not
acquired by the sensor. f measures the confidence
in the observation model; it is close to 0 if the obser-
vation equation is not valid.
Observation values with a low confidence will
then not be taken into account for the computation
of the state vector and for the solution of the Image
Processing problem.
4 DETERMINING OPTICAL
FLOW
Let I be a sequence of images on a spatial domain Ω
and W(x, t) be the velocity vector of a point x ∈ Ω at
time t. The velocity vector is expressed by the Optical
Flow Constraint equation (Horn and Schunk, 1981):
∇I
T
(x, t)W(x, t) +
∂I
∂t
(x, t) = 0 ∀x ∈ Ω (20)
This is an ill-posed problem: the velocity vector has
two components and the optical flow equation is not
sufficient to compute both. A solution can be ob-
tained using Tikhonov’s method by constraining spa-
tially (Horn and Schunk, 1981) or spatially and tem-
porally (Weickert and Schn¨orr, 2001) the solution.
Let us explain, advantages of the data assimilation
methods on this simple example.
4.1 Observation and Evolution Models
W(x, t) is considered as the state vector X(x, t) and
the image gradients (∇I(x, t), I
t
(x, t)) constitutes the
observation vector Y(x, t). By identification in (3)
and (20), the observation model is:
(W, I) = ∇I(x, t)
T
W(x, t) + I
t
(x, t) (21)
To determine a suitable observation error co-
variance handling missing data, we use equa-
tions (17), (18) and (19) to define the inverse covari-
ance. f
noise
is assumed to be equal to 1 without further
information. f
sensor
is set to 0 where data are not ac-
quired and to 1 otherwise. f is chosen from the fol-
lowing remark: on a sequence of images with regions
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
598

of uniform grey level values, the spatio-temporal gra-
dient is null on these regions and equation (20) is de-
generated. For avoiding considering these points, f
is:
f (x,t) = 1− exp(−k∇
3
I(x, t)k
2
) (22)
where ∇
3
denotes the spatio-temporal gradient. The
observation model being scalar, r
0
and r
1
are scalar
and respectively set to ε and 1 − ε with ε ∼ 10
−6
.
The transport of the velocity is chosen as evolution
equation. The evolution model is:
(W) =
1
(W)
2
(W)
=
UU
x
+VU
y
UV
x
+VV
y
T
with (U,V)
T
= W.
Let us denote I
2
the 2×2 identity matrix. Q is cho-
sen as:
Q(x, t, x
′
,t
′
) = I
2
exp(−
1
σ
(kx− x
′
k + |t−t
′
|)) (23)
to ensure a first-order spatial regularization.
We choose the Horn and Schunk’s algorithm to
compute the velocity field on the first image of the se-
quence. This initial condition is supposed to be with-
out errors: B(x, x
′
) = δ(x− x
′
).
4.2 Adjoint Operators
In order to determine the adjoint operators of
and , the directional derivatives must first be estab-
lished.
Using the definition (6), we obtain:
∂
1
∂W
(η) =
∂
1
∂U
(η
1
) +
∂
1
∂V
(η
2
)
= Uη
1
x
+U
x
η
1
+Vη
1
y
+U
y
η
2
∂
2
∂W
(η) =
∂
2
∂U
(η
1
) +
∂
2
∂V
(η
2
)
= Uη
2
x
+V
y
η
2
+Vη
2
y
+V
x
η
1
with η =
η
1
η
2
T
. By definition (14) and consid-
ering border terms equal to zero, the adjoint operator
of is :
∂
1
∂W
∗
(λ) = −Uλ
1
x
−V
y
λ
1
−Vλ
1
y
+U
y
λ
2
∂
2
∂W
∗
(λ) = −U
x
λ
2
−Uλ
2
x
−Vλ
2
y
+V
x
λ
1
with λ =
λ
1
λ
2
T
.
The directional derivative of the observation operator
is:
∂
∂W
(η)(x,t) = ∇I
T
(x, t)η(x, t)
and the adjoint operator is:
∂
∂W
∗
(λ)(x,t) = ∇I(x,t)λ(x,t)
4.3 Discretization
Using the choices explained in Subsection 4.1, the
three PDEs (9,11,13) become:
∂W
∂t
+ W
T
∇W = 0 (24)
−
∂λ
∂t
− ∇λ
T
W− λ
T
∇
⊥
W = A⋆ L (25)
∂δW
∂t
+ W
T
∇δW+ ∇W
T
δW = Q⋆ λ (26)
with: A = −
1
2σ
2
∇IR
−1
, L = I
t
+ ∇I
T
(W + δW),
∇
⊥
W =
∇
⊥
U ∇
⊥
V
and ∇
⊥
U =
U
y
−U
x
T
.
These three equations are further approximated using
the finite difference technique.
As W(x, t) is a vector of
2
, equation (24) has
two components. The first one combines a linear ad-
vection in direction y and a non linear in direction
x. A direct approximation leads to an unstable nu-
merical scheme. In (Papadakis et al., 2007a), the
scheme is stabilized by introducing a diffusive term
with the drawback to smooth the solution. We pro-
pose an alternative to stabilize the numerical scheme
associated to the original equation, as explain in the
following. The first component of equation (24) is
first expressed as a two-equation system using a split-
ting method (Verwer and Sportisse, 1998):
∂U
∂t
+UU
x
= 0 (27)
∂U
∂t
+VU
y
= 0 (28)
Equation (27) is rewritten using the Lax-Friedrich
method (Sethian, 1996) in the following form
∂U
∂t
+
∂F(U)
∂x
= 0 with F(u) =
1
2
u
2
. This new equation is
approximated by the explicit scheme:
U
k+1
i, j
=
1
2
(U
k
i+1, j
+U
k
i−1, j
) −
△t
2
(F
k
i+1, j
− F
k
i−1, j
)
with U
k
i, j
= U(x
i
, y
i
,t
k
), F
k
i, j
= F(U(x
i
, y
i
,t
k
)). The
term
1
2
(U
k
i+1, j
+ U
k
i−1, j
) stabilizes the numerical
scheme (by adding a diffusive effect) when △t has
a low value (the Courant-Friedrich-Levy condition).
The linear advection (28) is approximated using a
shock explicit scheme (Sethian, 1996):
U
k+1
i, j
= U
k
i, j
− △tS
x
(U
k
,V
k
)
i, j
SOLVING ILL-POSED PROBLEMS USING DATA ASSIMILATION - Application to Optical Flow Estimation
599

with S the shock operator, defined in the x-direction
by: S
x
(U,V)
i, j
= max(V
i, j
, 0)(U
i, j
− U
i−1, j
) +
min(V
i, j
, 0)(U
i+1, j
−U
i, j
).
It can be seen that the second component of (24)
contains a linear advection term in direction x and a
non linear advection term in direction y. The same
strategy is then used to perform the discretization
process.
Equation (25) combines a linear advection, a term
of reaction and a forcing term. It also has two com-
ponents. The first is −
∂λ
1
∂t
− Uλ
1
x
− V
y
λ
1
− Vλ
1
y
+
U
y
λ
2
= A
1
⋆ L with A
1
= −
1
2σ
2
I
x
R
−1
. It is split into
two parts. The first one contains the linear advection
in direction x and the reaction term −
∂λ
1
∂t
− Uλ
1
x
−
V
y
λ
1
= 0 and is approximated in the same way as (28)
with an explicit shock scheme. However, the equation
is retrograde as the initial condition is given at time T:
(λ
1
)
k−1
i, j
=
1+
1
2
(V
k
i, j+1
−V
k
i, j−1
)
(λ
1
)
k
i, j
+
△tS
x
((λ
1
)
k
,U
k
)
The second part contains the linear advection term
in direction y and the forcing term: −
∂λ
1
∂t
− Vλ
1
y
+
U
y
λ
2
= A
1
⋆ L. Again, a shock explicit scheme is used:
(λ
1
)
k−1
i, j
= (λ
1
)
k
i, j
−
△t
2
U
k
i, j+1
−U
k
i, j−1
(λ
2
)
k
i, j
−
△t(A
1
⋆ L)
k
i, j
− △tS
y
((λ
1
)
k
,V)
Having the same structure as the first component, the
second component of (25) is approximated using the
same method
The last equation, (26), is similar to equation (25)
and the same discretization technique is applied.
4.4 Results
The “taxi” sequence and a synthetic sequence have
been chosen for discussing results. For both cases, the
initial condition is provided by the Horn and Schunk
method applied on the two-first frames of the se-
quence. Image gradients, providing observations, are
computed with a convolution method and a derivative
Gaussian kernel. The parameter σ of the matrix Q is
set to 1. The number of iterations is set to 5.
The taxi sequence displays several cars with a
slow and quasi uniform motion.
In a first experiment, we compute the optical flow
on the sequence using the Data Assimilation method
(D.A.). The Horn & Schunk method (H.&S.) is also
applied and results, on the fifth frame, are displayed
Figure 1: Result on frame 5: D.A. (top), H&S (bottom).
for comparison purposes on Figure 1. Results of both
methods are similar in this case because observation
values are available on the whole sequence obviously.
Having chosen H.&S. or another method does not re-
ally matter. The issue is not comparing optical flow
method but proving the efficiency of D.A. for missing
data or complex dynamics. Then, a second experi-
ment is designed to prove the capability of D.A. to
manage missing data. To simulate a sensor failure,
a large region around the white car is set to zero in
a frame and the function f
sensor
returns zero on these
pixels. Image gradients are then computed. Figure 2
shows the results for D.A. and H.&S. methods. This
latter obviously fails to provide acceptable velocity
vectors over the missing data region while D.A. suc-
cesses due to the eviction of aberrant values in the
computation. Even a whole frame of observation can
be missing: we force image gradient values to zero
on the fifth frame of the taxi sequence and f ≡ 0
on this frame. Figure 3 displays results obtained with
D.A. with and without image gradients observation on
frame 5. Results are similar, due to the fact that the
evolution model correctly describes the temporal dy-
namics of the sequence and compensate missing data.
H.&S. method is no more able to provide any result in
that case, conducting to a discontinuity in the output.
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
600

Figure 2: Missing data: D.A. (top), H.&S. (bottom).
A third experiment is dedicated to the demonstra-
tion that the evolution model improves the estimation
of the image dynamics. For that purpose, we build
a synthetic sequence with two squares, one moving
horizontally and one vertically. At the end of the se-
quence, they meet each other. Figure 4 shows the re-
sult of both methods at the beginning and the end of
the sequence. H.&S.’s method fails to estimate a cor-
rect velocity direction when the squares meet. This is
a common drawback of image processing method due
to over regularization. D.A. however provides accu-
rate results: the evolution model correctly describes
the squares dynamics and decreases the effect of spa-
tial regularization.
5 CONCLUSIONS
In this paper we described a framework to solve ill-
posed Image Processing problems using Data Assim-
ilation algorithms. This approach is an alternative
to the Weickert’s method, which constrains the solu-
tion’s variations in space and time.
General principles to choose a suitable evolution
model, an observation equation, and their matrices
of covariance were discussed in the paper. The ob-
Figure 3: Result with gradients set to zero on frame 5 (top)
and with gradient available (bottom).
servation equation corresponds to the Image Model
of the Tikhonov regularization method. The evolu-
tion equation constrains the solution in time and the
model error constrains it in space. As an illustration,
we proved that an exponential covariance model er-
ror is equivalent to a first order Tikhonov regulariza-
tion. The three drawbacks of the Weickert’s method,
pointed out in the Introduction, are overcome. First,
the state vector’s dynamics is described by a suitable
evolution model. Second, a covariance R built from
the confidence on the observation values weights the
influence of these latter: observations having a low
quality, such as missing data, are not taken into ac-
count in the computation of the solution. And last,
the algorithm processes a sequence of images frame
by frame, which allows an implementation with low
memory requirements. The choice of the evolution
model remains a key point as it greatly depends on
the applicative context. We described it in the case
of determining optical flow: image’s grey level values
are assimilated in an evolution model representing a
transport equation of the velocity and a stable numer-
ical scheme, approximating this equation, has been
established.
The main perspective of the work is to define a
SOLVING ILL-POSED PROBLEMS USING DATA ASSIMILATION - Application to Optical Flow Estimation
601

(a) frame 4
(b) frame 10
Figure 4: Result with D.A. (left) and H.&S. (right).
generic form of the evolution model which will then
be specified depending of the Image Processing ap-
plication. Diffusion laws, modelling the transport of
the state vector using the physical conservative prin-
ciples, are good candidates for a number of reasons.
First, their approximation in a discrete space is robust
as stable numerical schemes exist. Second, the adjoint
of the model operator is known explicitly. Third, sev-
eral types of diffusion can be considered depending
on their impact on the spatial and temporal regulariza-
tion of the solution. An isotropic diffusion is equiva-
lent to a uniform regularization but has the drawback
to smooth the solution while an adaptive diffusion,
driven by the state vector, allows discontinuities to be
preserved. As the spatial regularization may also be
performed by the covariance matrix Q, it could be in-
teresting to compare the two paradigms. Moreover,
the diffusion can also be driven by the observation
values or by their confidence. For instance, a strong
diffusion on the state vector may operate when the
observation confidence is low which is an alternative
way to deal with missing data. Again, a comparison
between such a diffusion and the covariance matrix R
built from the observation confidence must be led.
REFERENCES
B´er´eziat, D. and Herlin, I. (2008). Solving ill-posed image
processing problems using data assimilation. Applica-
tion to optical flow. Research Report 6477, INRIA.
Hadamard, J. (1923). Lecture on Cauchy’s Problem in Lin-
ear Partial Differential Equations. Yale University
Press, New Haven.
Horn, B. and Schunk, B. (1981). Determining optical flow.
Artificial Intelligence, 17:185–203.
Huot, E., Herlin, I., and Korotaev, G. (2008). Assimila-
tion of sst satellite images for estimation of ocean
circulation velocity. In Proceedings of IEEE Inter-
national Geoscience and Remote Sensing Symposium
(IGARSS), Boston, Massachusetts, U.S.A.
Oliver, D. (1998). Calculation of the inverse of the covari-
ance. Mathematical Geology, 30(7):911–933.
Papadakis, N., Corpetti, T., and M´emin, E. (2007a). Dy-
namically consistent optical flow estimation. In Pro-
ceedings of International Conference on Computer Vi-
sion, Rio de Janeiro, Brazil.
Papadakis, N., H´eas, P., and M´emin, E. (2007b). Im-
age assimilation for motion estimation of atmospheric
layers with shallow-water model. In Proceedings of
Asian Conference on Computer Vision, pages 864–
874, Tokyo, Japan.
Papadakis, N. and M´emin, E. (2007). Variational optimal
control technique for the tracking of deformable ob-
jects. In Proceedings of International Conference on
Computer Vision, Rio de Janeiro, Brazil.
Sethian, J. (1996). Level Set Methods. Cambridge Univer-
sity Press.
Tarantola, A. (2005). Inverse Problem Theory and Methods
for Model Parameter Estimation. Society for Indus-
trial and Applied Mathematics.
Tikhonov, A. N. (1963). Regularization of incorrectly posed
problems. Sov. Math. Dokl., 4:1624–1627.
Valur H´olm, E. (2003). Lectures notes on assimilation
algorithms. Technical report, European Centre for
Medium-Range Weather Forecasts Reading, U.K.
Verwer, J. and Sportisse, B. (1998). A note on operator
splitting in a stiff linear case. Technical Report MAS-
R9830, Center voor Wiskunde en Informatica.
Weickert, J. and Schn¨orr, C. (2001). Variational optic flow
computation with a spatio-temporal smoothness con-
straint. Journal of Mathematical Imaging and Vision,
14:245–255.
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
602
