
A NEW NON-REDUNDANT SCALE INVARIANT INTEREST POINT
DETECTOR
Luis Ferraz
Department of Computing Science, Universitat Autonoma de Barcelona, Barcelona, Spain
Xavier Binefa
Department of Information and Communication Technologies, Universitat Pompeu Fabra, Barcelona, Spain
Keywords:
Interest points extraction, Gaussian curvature, Scale space.
Abstract:
In this paper we present a novel scale invariant interest point detector of blobs which incorporates the idea of
blob movement along the scales. This trajectory of the blobs through the scale space is shown to be valuable
information in order to estimate the most stable locations and scales of the interest points. Our detector
evaluates interest points in terms of their self trajectory along the scales and its evolution avoiding redundant
detections. Moreover, in this paper we present a differential geometry view to understand how interest points
can be detected. We propose analyze the gaussian curvature to classify image regions as elliptical (blobs) or
hyperbolic (corners or saddles).
Our interest point detector has been compared with Harris-Laplace and Hessian-Laplace detectors on infrared
(IR) images, outperforming their results in terms of the number and precision of interest points detected.
1 INTRODUCTION
Interest point detection algorithms have been shown
to be well suited for feature extraction. The main goal
of these algorithms is to allow the extraction of fea-
tures invariant to some viewing conditions. Scale in-
variant detectors estimate the location and the scale of
these features. Different scale invariant detectors have
been developed over the past few years and among
the most important we can find Laplacian of Gaus-
sian (LoG) (Lindeberg, 1998), Derivative of Gaus-
sian (DoG) (Lowe, 2004), Harris-Laplace (Mikola-
jczyk and Schmid, 2004), Hessian-Laplace (Mikola-
jczyk et al., 2005) or Maximally Stable Extremal Re-
gions (MSER) (Matas et al., 2002).
MSER produces good results in comparison with
other detectors but it is not analyzed in this paper
because of its bad performance on blurred images
(Mikolajczyk et al., 2005).
Typically, these detectors are based on a multi-
scale analysis of the image (Crowley, 1982). The
space-scale can be built using different scale normal-
ized operators, like Laplace filters or difference of
Gaussians filters. For these detectors an interest point
is detected if a local 3D extreme is present and if its
absolute value is higher than a threshold. Therefore,
blobs at different scales are not related and the same
blob can be detected many times along the scale-
space. To avoid this problem, our proposal is to es-
timate the trajectory of blobs along scales and select
the scale and location that best represent each blob.
From a differential geometry point of view im-
ages can be understood as surfaces with 3 types of
regions in function of their gaussian curvature: ellipti-
cal regions, parabolic regions and hyperbolic regions.
These types of regions allow to see images in a sim-
ple way, where elliptical regions can be understood as
blobs, parabolic regions as contours or plane regions
and hyperbolic regions as corners or saddles.
In order to extract this differential structure we use
the full Hessian matrix (DoCarmo, 1976) for each
point. This approach outperforms Laplacian based
operators more related to obtain rotational invariant
information (Lenz, 1992).
This paper is organized as follows. In section 2 the
method to detect interest points by means of curvature
analysis is introduced. In section 3 our scale invariant
interest point detector is described and finally, in Sec-
tion 4 we present experimental results.
277
Ferraz L. and Binefa X. (2009).
A NEW NON-REDUNDANT SCALE INVARIANT INTEREST POINT DETECTOR.
In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 277-280
DOI: 10.5220/0001802702770280
Copyright
c
SciTePress

2 CURVATURE ANALYSIS
The image behaviorin a local neighborhood of a point
x
0
can be obtained by the second order Taylor ap-
proach,
f(~x) = f(~x
0
) + ∇f(~x
0
)(~x− ~x
0
) (1)
+
1
2
∇
2
f(~x
0
)(~x− ~x
0
)
2
+ R(~x)
where the second term contains information about
the gradient distribution in a local neighborhood. Us-
ing this gradient informationcan be computed the first
fundamental form I (Equation 2). The next term is the
second fundamental form II (Equation 3) that con-
tains information about the shape near to x
0
. The last
term R(x) is referred to as the remainder, since it con-
tains the difference between the image f(~x) and its
representation.
I(~x
0
,σ) =
1+ f
2
x
(~x
0
,σ) f
x
f
y
(~x
0
,σ)
f
y
f
x
(~x
0
,σ) 1+ f
2
y
(~x
0
,σ)
(2)
II(~x
0
,σ) =
f
xx
(~x
0
,σ) f
xy
(~x
0
,σ)
f
yx
(~x
0
,σ) f
yy
(~x
0
,σ)
(3)
where σ is the scale normalization factor for the
space-scale.
The first and second fundamental forms of a sur-
face determine an important differential-geometricin-
variant, the Gaussian curvature K. The Gaussian cur-
vature of a point on a surface is the product of the
principal curvatures, K = k
1
∗ k
2
of the given point.
Moreover, Gaussian curvature can be expressed as the
ratio of the determinants of the second and first fun-
damental forms,
K =
det(II)
det(I)
(4)
The sign of the Gaussian curvature at a point de-
termines the shape of the surface near that point (Do-
Carmo, 1976): for K > 0 the surface is locally convex
(blob regions) and the point is called elliptic, while for
K < 0 the surface is saddle shaped (i.e. corners) and
the point is called hyperbolic. The points at which the
Gaussian curvature is zero (i.e. contours) are called
parabolic.
The first fundamental form is positive definite,
hence its determinant is positive everywhere. There-
fore, the sign of K coincides with the sign of the de-
terminant of the second fundamental form. Assuming
that point ~x
0
is a critical point (the gradient ∇f(~x
0
)
vanishes) the Gaussian curvature of the surface at ~x
0
is the determinant of II(~x
0
). So, it is not necessary to
calculate I(x
0
) to estimate the Gaussian curvature.
Figure 1: Saddle surface with normal planes in directions
of principal curvatures.
In Figure 1 is shown the meaning of curvature.
Given the normal vector to the point ~x
0
, its tangent
plane and its two principal curvatures k
1
and k
2
Gaus-
sian curvature is defined positive if both curvatures
have the same sign, negative if they have different
sign and zero if any curvature is zero.
3 OUR INTEREST POINT
DETECTOR OF BLOBS
In this section we propose a new scale invariant in-
terest point detector of blobs based on the analysis of
Gaussian curvature of the image along the space-scale
representation. Moreover, to obtain more stable inter-
est points the trajectory of each one is extracted.
The evolution of blobs along scales was studied in
depth by (Lindeberg, 1993). Traditionally, the anal-
ysis of the behavior of blobs presents severe compli-
cations, since it implied a detailed description of the
image. However, for our purposes we do not need
a precise description and one of the important con-
tributions of our work is to reduce the detail of the
analysis since we only need an approximation of the
movement of blobs.
Figure 2: Trajectory of some blobs along scales (blue lines).
Blob movements and blob fusions can be seen. Green points
show all the extremes found. Red points are the extremes
selected as interest points.
To obtain this approximation, in first place a
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
278
space-scale representation must be build. Scale nor-
malized second fundamental form (Equation 3) is
used in order to obtain it calculating the Gaussian cur-
vature K associated to each point of each scale.
All the maxima are computed for each scale to
find all the blobs. Once obtained, they must be an-
alyzed to put them in correspondence. Blobs found in
consecutive scales are linked using a gradient ascent
propagation algorithm to find the nearest and plausi-
ble link. As a result of this step, the pipe/trajectory of
each blob is obtained. Experimentally, we have seen
that using this simple strategy provides a coherent and
good approximation of the trajectories.
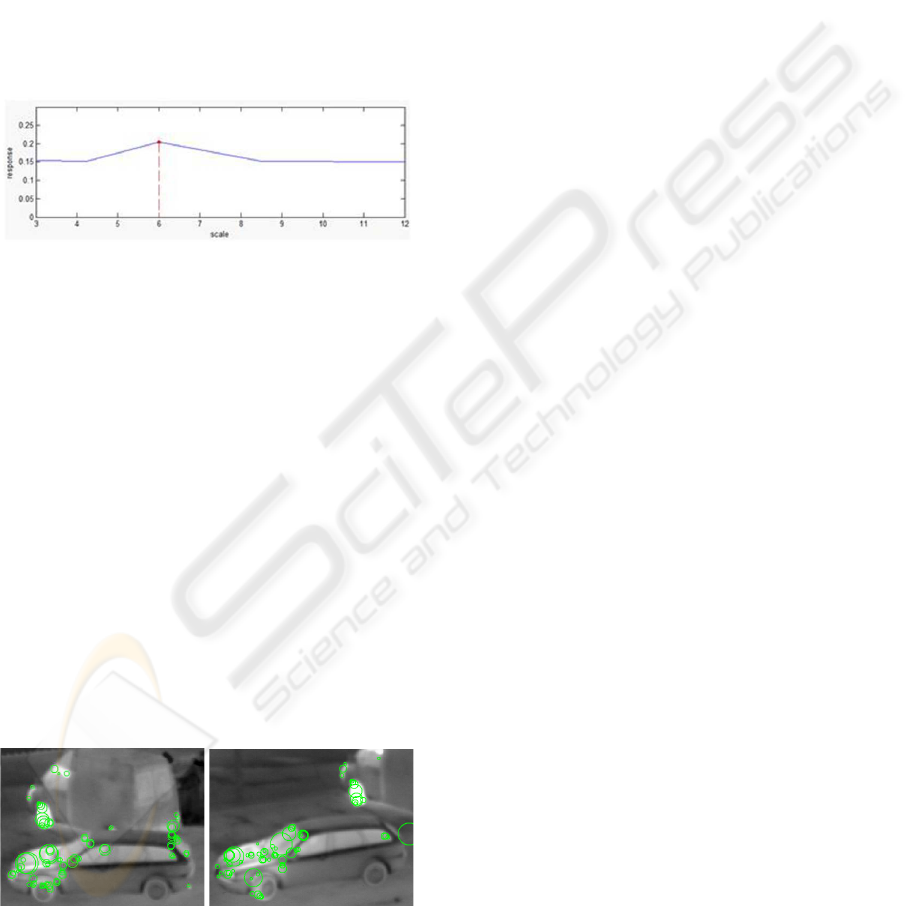
Figure 3: Example of values for the Gaussian curvature
along scales given one blob trajectory.
The last step consists on obtaining from each blob
trajectory which are those locations that maximize
their Gaussian curvature compared with their nearest
neighbors in the pipe (Figure 3).
4 EXPERIMENTAL RESULTS
IR images are thermal images that contain a high sig-
nal to noise ratio and a lack of contrast, so blurred
images are obtained. We have compared our method
with two typical interest point detectors that have
proved, accordingly to literature, that produce good
results: Harris-Laplace and Hessian-Laplace. The
first one is based on the detection of corners that are
representative along the space-scale and the second
one on the detection of blobs.
Figure 4: Example of interest points detected using Harris-
Laplace detector (green circles symbolize location and
scale) on two different images of an IR sequence. Com-
paring detected points on the images is shown that interest
points are unstable.
Harris-Laplace detector calculates corners at the
different scales using a scale adapted Harris opera-
tor. After that, locations of detected corners are eval-
uated with a Laplacian filter in the superior and infe-
rior scales. Interest points correspond to corners with
a maximal response of Laplacian filter.
Harris-Laplace detector has been applied on IR
images to test its performance on these images. As
Harris-Laplace detector is based on Harris operator
and therefore, since in IR images corners are not
sharpened, it produces bad results in contrast with
Hessian-Laplace. Figure 4 show that Harris-Laplace
detector produces unstable interest points in IR im-
ages. Therefore, the same object viewed from differ-
ent points of view produces interest points in different
locations and scales. Moreover, Figure 4 shows that
the same interest point is detected in different scales
using this detector.
Hessian-Laplace detector works in a similar way
to Harris-Laplace detector(Mikolajczyk et al., 2005).
The main difference is that instead of Harris opera-
tor uses a function based on the determinant of the
Hessian matrix to penalize very long structures (for
example it is useful to discard contours detected as
blobs).
Given that Harris-Laplace produces unstable re-
sults the final comparison has been done between
Hessian-Laplace detector and our blob detector.
These two detectors are based on the detection of
blobs, differing in two ways: the method to decide
which neighbors around extremes must be analyzed
and the function applied to extreme detection.
Comparing Hessian-Laplace and our detector is
where the power of our algorithm is shown in a best
way. Figure 5 compare these two algorithms show-
ing that Hessian-Laplace detects a high quantity of
interest points being the most of them redundant. Our
detector practically does not produce redundancy be-
cause of trajectory of blobs gives information about
the best scale. Moreover, our detector seems to find
interest points closest to our perception that the other
one.
5 CONCLUSIONS
We have presented a powerful mechanism to detect
the most stable locations of blobs by estimating their
trajectory along scales. By means of this trajectory
the best locations and scales for each point can easily
be selected. Moreover, by using the Gaussian curva-
ture we classify regions on images in a simple way.
We have shown that over IR images those inter-
est point detectors based on corner detection do not
A NEW NON-REDUNDANT SCALE INVARIANT INTEREST POINT DETECTOR
279

(a) (b)
(c) (d)
(e) (f)
(g) (h)
Figure 5: Hessian-Laplace versus our detector. (a), (c), (e)
and (g) show the Hessian-Laplace results over 4 IR images.
(b), (d), (f) and (h) show the results of our detector over the
same 4 IR images. Red circles symbolize the locations and
scales of interest points.
produce satisfactory results, due to the lack of sharp-
ness of the contours. It is also a fact that interest point
detectors based on blob detection, although they pro-
duce good results, most of them are redundant.
By comparing these blob detectors with our pro-
posed detector we show that our algorithm works fine,
producing promising results. It also opens future re-
search lines around blob trajectories along scales and
Gaussian curvature analysis using first and second
fundamental forms. Moreover, an extension to the
detection of affine blobs could be done by analyz-
ing in depth the Gaussian curvature surface generated
around each interest point.
Finally, we want to remark that our detector has
been tested mainly on IR images. However, tests done
on gray level images have produced similar results.
ACKNOWLEDGEMENTS
This work was produced thanks to the support of the
Universitat Aut`onoma de Barcelona. Thanks are also
due to Tecnobit S.L. for yielding the car sequence im-
ages.
REFERENCES
Crowley, J. L. (1982). A representation for visual informa-
tion with application to machine vision. PhD thesis.
DoCarmo, M. P. (1976). Differential Geometry of Curves
and Surfaces. Prentice-Hall.
Lenz, R. (1992). Group theoretical feature extraction:
Weighted invariance and textulre analysis. In The-
ory & Applications of Image Analysis: Selected Pa-
pers from the 7th Scandinavian Conference on Image
Analysis, pages 63–70.
Lindeberg, T. (1993). Scale-Space Theory in Computer
Vision (The International Series in Engineering and
Computer Science). Springer.
Lindeberg, T. (1998). Feature detection with automatic
scale selection. International Journal of Computer Vi-
sion, 30:77–116.
Lowe, D. G. (2004). Distinctive image features from scale-
invariant keypoints. International Journal of Com-
puter Vision, 60:91–110.
Matas, J., Chum, O., Urban, M., and Pajdla, T. (2002). Ro-
bust wide baseline stereo from maximally stable ex-
tremal regions. In In British Machine Vision Confer-
ence, pages 384–393.
Mikolajczyk, K. and Schmid, C. (2004). Scale & affine in-
variant interest point detectors. International Journal
of Computer Vision, 60:63–86.
Mikolajczyk, K., Tuytelaars, T., Schmid, C., Zisserman, A.,
Matas, J., Schaffalitzky, F., Kadir, T., and Van Gool,
L. (2005). A comparison of affine region detectors.
International Journal of Computer Vision, 65:43–72.
VISAPP 2009 - International Conference on Computer Vision Theory and Applications
280
