Semi-Automatic Modeling of Bones for Real-Time

Surgery Support

Roger Cuypers, Benjamin Weyers and Wolfram Luther

Insititute of Computer Science and Cognitive Science, University of Duisburg-Essen

Lotharstr. 65, Duisburg, Germany

Abstract. Model-based reconstruction of human bones for surgical purposes is

an upcoming field of research in informatics and kinematics. Tools for planning

surgeries and real-time support require appropriate mathematical models for

rendering, interacting and reconfiguration. It is our conviction that superquad-

rics offer this powerful mathematical modeling capability. Image-based data

from MRI and X-ray examinations have to be extracted and gathered to 3D-

point sets, which are afterwards fitted by superquadric-based models. The fit-

ting process is complex and time-consuming. To solve this problem and to pro-

vide real-time simulation for surgical support, it is necessary to apply the

knowledge of the expert user. This paper presents the concept and a prototypi-

cal implementation of an interactive system that involves the user in the fitting

process to accelerate the calculation and enhance the resulting model.

1 Introduction

Recently, computer-based pre-operative planning has come to be considered a very

important practice for giving the surgeon a detailed understanding of the complex

interior body structure and the effects of possible treatment approaches. For this rea-

son, methods and models for manipulating and processing components of the human

skeletal system in an intuitive and efficient manner have become a topic of practical

importance in the development of appropriate computer-based skeletal crafting and

simulation tools.

One of the drawbacks of existing tools is the fact that most of them are still

closely oriented towards traditional generic computer-aided construction applications

that allow only simple navigation and surface manipulation using primitive geometric

shapes. The resulting modeling reflects neither the topology of the bone nor the inten-

tions of the surgeon sufficiently.

This paper presents a task-oriented, computationally efficient and flexible geo-

metric modeling approach for a skeletal component classification, reconstruction and

manipulation tool together with an effective interface that exposes the capabilities of

the model to the user in an intuitive manner.

Cuypers R., Weyers B. and Luther W. (2009).

Semi-Automatic Modeling of Bones for Real-Time Surgery Support.

In Proceedings of the 1st International Workshop on Medical Image Analysis and Description for Diagnosis Systems, pages 13-23

DOI: 10.5220/0001814000130023

 SciTePress

2 Prior Research

The generation of customized geometric models from 3D point cloud data has been

the subject of extensive research. In medical applications, the geometrical models

were mainly selected due to their capability of giving an exact reproduction of the

bone surface. Popular models are triangle meshes [8], [18] or octrees [14]. Martin et

al. [12] use B-spline surfaces to model a femur’s cortical and trabecular part. Kura-

zume et al. [9] use a statistical shape model whose parameters can be extracted from

two 2D fluoroscopic images. However, feature-extraction algorithms that make use of

these models receive very little beforehand-information about the global features of

the bone that help them with their tasks. Furthermore, overall handling of the recon-

structed models by the user is difficult due to their high number of parameters.

Of special interest are implicit superquadric (sq) models, which, due to their high

modeling power and their well-behaved mathematical nature, proved a powerful tool

for modeling even complex surface topologies. Originally invented by Barr in 1981,

the usage and capabilities were greatly improved in papers by Solina and Metaxas by

providing advanced deformation [6] and blending [16]. Zhou et al. [19] further ex-

tended the sq-model by replacing the exponents of the inside/outside function with

Bezier curve functions, thus making it possible to increase surface complexity to an

arbitrary level. Others tried to enhance accuracy by raising the number of components

within the model.

There are several approaches that target a fully automatic generation of sq-models

from scattered 3D point data. Chevalier et al. [3] introduce a split-and-merge ap-

proach to generate a composite model of several SQs. All these approaches are ge-

neric in nature and do not make use of any a priori knowledge that could improve the

result leading to an optimal approximation of the actual bone surface. A sophisticated

fitting approach that considers the specific bone geometries and allows basic user

interaction has been studied in the context of the ongoing PROREOP project and is

proposed in [4].

The special and complex geometric nature of the human bone requires a model-

generating process to gather as much information as possible about the object of

interest in order to generate an optimal result. This can best be achieved by providing

the user with the ability to influence the fitting process and the parameter flow. Since

the final application should be suitable for clinical environments, a comfortable user

interface is mandatory. Therefore, this paper introduces a sophisticated sq-based

selection tool that allows the user to intuitively steer the fitting process by helping the

system identify and classify the relevant data and parameters whenever necessary.

3 Bone Modeling

The aim of our research on human skeletal modeling was to produce a geometric

model of a given set of lower-limb bones that could later be used for kinematical

simulation. The model should be able to reproduce the bone surface as exactly as

possible while keeping the processing time short enough for real-time use. SQs offer

the power to model a great variety of shapes from only a few parameters, which

makes the search for appropriate parameter sets very efficient. Their dual implicit-

parametric nature also allows straight-forward rendering approaches using widely

available 3D programming interfaces like OpenGL.

3.1 Superquadrics

An SQ-surface is an implicit surface in 3D space that consists of all the points (x, y,

z) with [1]:

),,(

εε

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

≡

zyxF

= 1 .

(1)

The parameters a

, a

and a

specify the scale of the shape in x, y and z direction, and

and ε

define its roundness. This surface can be fitted to a 3D point cloud by mini-

mizing a distance function that measures the proximity of the points to the surface.

The distance function is defined by the radial Euclidean distance between a point and

a superellipsoid, which reads as:

d( A, x, y, z ) = F

(x, y, z) - 1 .

(2)

where A is the surface, (x, y, z) are the points and F is the inside-outside function

from formula (1) that yields 1 for points that lie on the surface, < 1 for points that lie

inside and > 1 for points that lie outside the shape.

Next to the simple superellipsoidal model in Formula 1, a supertoroidal model

supports toroidal shapes. Additionally, Solina [6] proposes an extended SQ model

supporting tapering and bending. This allows for the modeling of a greater class of

shapes, which benefits the design of bone representations introduced in the following

section.

3.2 Superquadric Fitting

To fit an SQ to a set of 3D data points, it is necessary to determine a set of model

parameters for which the distance between the SQ surface and the point cloud is

minimized. The method used in this paper was introduced by Solina [15] and repre-

sents a least squares fit that minimizes the sum expression in Formula (3) which

measures the radial euclidean distance defined according to formula (2)

()

321

1),,(min

∑

−

iii

zyxFaaa

(3)

where n is the number of input 3D points. This nonlinear optimization task is solved

by using a sequential quadratic programming method.

In order to optimize the quality of the fit, three conditions must be met:

 The initial guess for the parameter set should already be close to the actual val-

ues; the algorithm used performs a local optimization.

 The selection of the point cloud fragment serving as input should span the tar-

get geometry as exactly as possible.

 The selection should resemble a shape that can be closely approximated by an

SQ.

To achieve this goal, the semi-automatic approach introduced in this paper includes

an extended selection tool that allows the user not only to define outlines that resem-

ble simple geometrical objects, like cubes or spheres, but also to use true sq-shapes

for the selection. This improves the fit, firstly, by delivering an area with an optimal

sq-shape and, secondly, by providing a parameter set that represents a close initial

surface approximation. The complete procedure of the interactive fit together with the

user interface is described in section 4 (below).

3.3 Superquadric Bone Modeling

Fig. 1 shows implemented versions of the generic femur and hip models.

Fig. 1. Generic SQ models of hip and femur.

The bones are decomposed into several SQ primitives oriented in an analytic descrip-

tion of the bone shapes supplied by Goldfinger [5]. Each bone model is therefore

reconstructed by fitting the SQs from the generic model to the 3D point clouds repre-

senting the respective parts of the bone. To perform this task, the significant bone

parts are labeled beforehand, either by a fully automatic approach (which several tests

have found unreliable) or by a semi-automatic approach, which is introduced in sec-

tion 4 (below).

4 Interactive Fitting Process

In order to optimize the described fitting algorithm (section 3.2), we developed an

interactive pre-fitting process, which is introduced in this section. This interactive

process involves the following two major aspects:

1. The

decomposition of a given 3D point cloud into fragments, which includes (a)

the definition of point sets approximating the target geometry as exactly as possi-

ble and (b) the identification of ideal initial values for the fitting algorithm.

2. The classification of several parts of the geometrical model, which provides in-

formation necessary for the calculation of characteristic bone features like those

listed in Table 1.

Table 1. A selection of characteristic features from the femur and hip bone.

Femur Hip

Femur axis origin ASIS position

Femur axis direction PSIS position

Femur head center Hip joint center (left, right)

Femur head diameter Pelvis origin

Greater trochanter tip Pelvis orientation

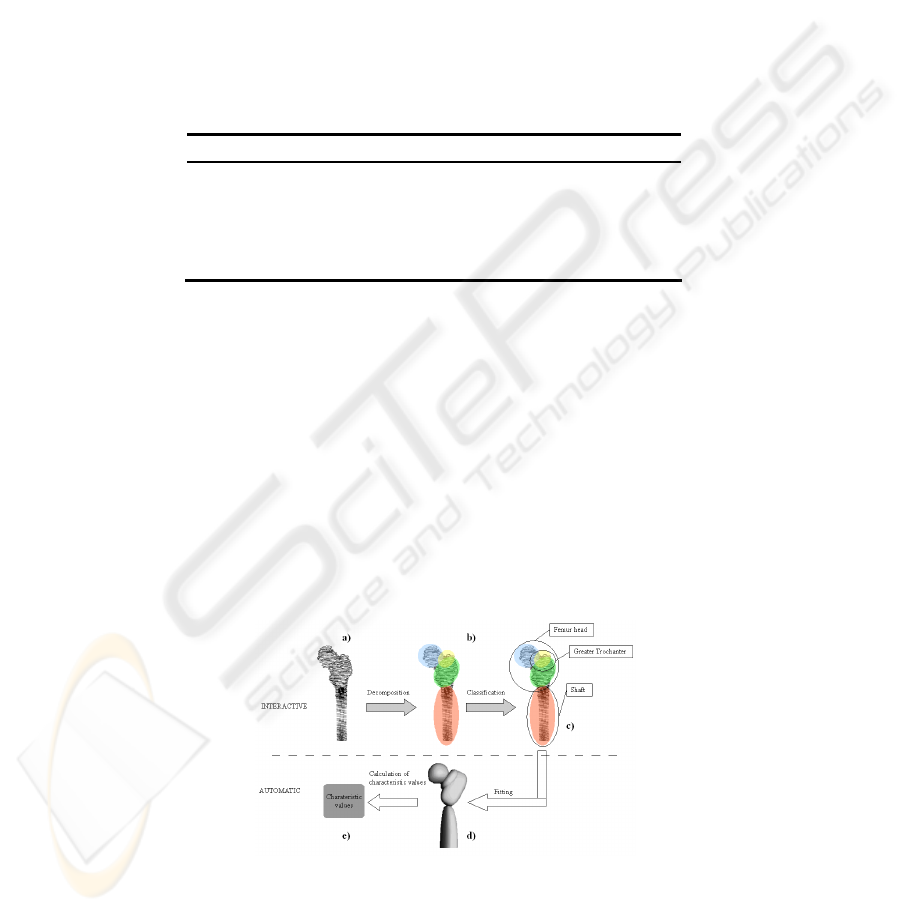
Fig. 2 shows how decomposition and classification are integrated in an interactive

workflow. Beginning with a data cloud of 3D points, the user starts by defining sub-

sets of points that are close to a functional fragmentation of the bone (as shown in

Fig. 1 for the femur: femur head as sphere, femur shaft as cylinder etc.) and a possible

model based on sq-geometries (section 3.1). To this end, we have implemented an

interactive selection tool based on an sq-geometry. After finishing the decomposition,

the user classifies the subsets according to the individual functions of the bone parts.

This classification is comparable to a tagging operation in a tagging system [11].

After the classification step in the workflow, the user’s task is to start the auto-

matic fitting process. The fitting algorithm first extracts information from the interac-

tive process and then calculates the sq-model for the given bone (section 3.3). From

the geometric model, the characteristic values are automatically extracted and pre-

sented to the surgeon.

Fig. 2. Selection tool, based on the basic sq-model.

4.1 Data Decomposition

The main aim of data decomposition in the context of surgical support and modeling

of bones from patient data (CRT or X-ray images) is the identification and fragmenta-

tion of the bone into its functional parts. A fully automatic approach to the identifica-

tion resulted in a less precise and unsatisfying fitting result (see section 5, below).

Therefore, the data decomposition in the process is a candidate for user intervention

(shown in Fig. 2), resulting in a more efficient and precise fitting result.

For the manual decomposition of the initial point cloud (Fig. 2, [a]), which results

from a prior segmentation process, the user interface has to offer an interactive selec-

tion tool feasible for a 3D environment. Like a spoon, the tool should separate a sub-

set of the initial point cloud using basic drag-and-drop operations combined with

transformation operations, like scaling and deforming the shape of the tool. Based on

the 3D engine for mechanical multi-body modeling and simulation called MOBILE

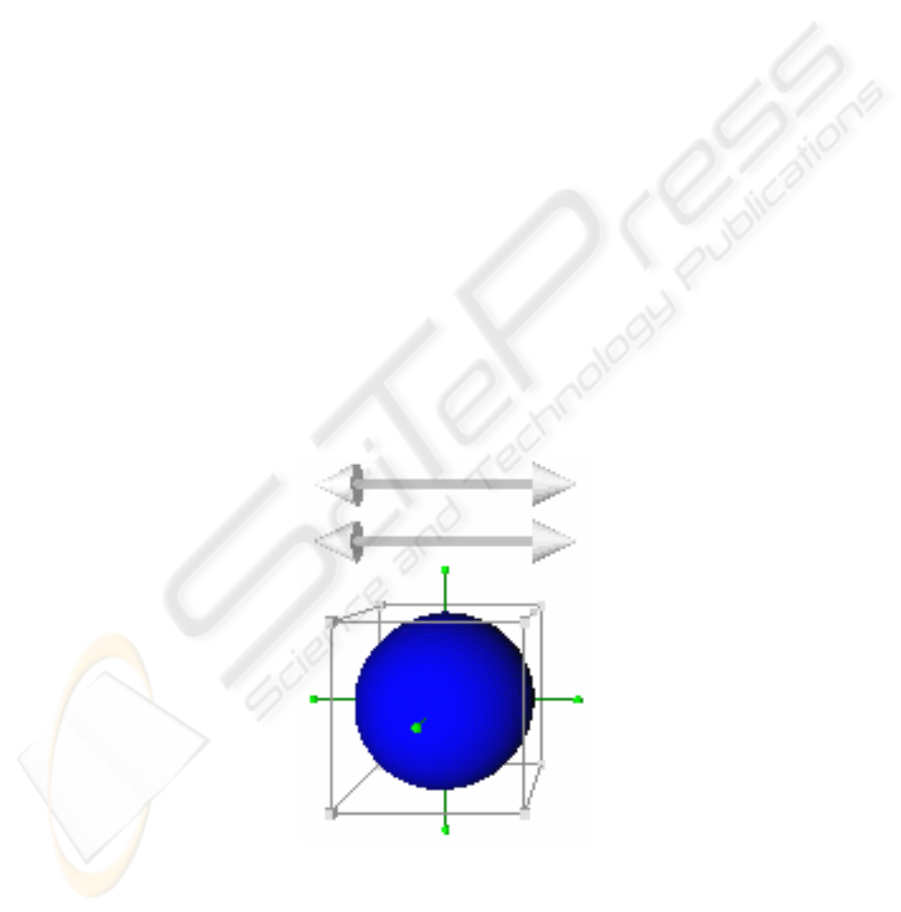
[7], we have developed selection tools that consist of an SQ paired with the complex

dragger component of the Inventor [17] library shown in Fig. 3. This implementation

combines several operations, including translation, rotation and scaling, on an sq-

model that result in a tool for precise positioning and selection in a 3D point cloud.

There are several reasons for using an sq-geometry in the tool. First, the geometry is

closely connected to the fitting process because the result of the fitting is a bone,

modeled as a set of SQs. By using SQs for selection, the fitting algorithm is initial-

ized with an adequate SQ (see section 3, above). Second, it is easy to test whether a

point in the point cloud belongs to the selected subset or not using the SQ’s inside-

outside function (see equation 1). Evaluating the inside/outside function which re-

quires only few parameters is much more efficient than testing a point’s position

against complex surfaces like B-spline or free-form surfaces, making this tool spe-

cially suited for achieving real-time processing.

Fig. 3. Selection tool, based on the basic superquadric model.

Depending on their definition, SQs have additional parameters that influence their

shapes. For the basic sq-model introduced in section 3 (see above), the parameters

and

define the roundness. Therefore, our selection tool shown in Fig. 3 offers

two 3D-dragger widgets for manipulation.

For each of the two above-mentioned models, the basic one and the deformable

one, an adequate selection tool has been implemented that grants access to all of the

model’s parameters. Each change to a parameter immediately updates the tool’s

shape. Due to the low complexity of the mathematical model, this update can be

achieved in real-time on state-of-the-art, especially with a high-end GPU-

implementation.

After selecting an area of the point cloud by having the SQ surround it, the user

presses a button to create the input-subset for the fitting algorithm. The resulting

information from this selection process is (a) the point-subset on which one SQ

should be fitted and (b) a set of initial sq-parameters directly given by the tool itself.

This approach supersedes the automatic fragmentation of the original point cloud

because of the expert knowledge of the user. It results in a faster and more precisely

fitted sq-model. Fig. 2 and 3 provide a comparison of a manual measurement ap-

proach with the semi-automatic approach using the additional data described.

Fig. 4. Example of finished data decomposition.

4.2 Component Classification

Classification of the defined point subsets in the sq-model is closely related to the

data decomposition step. After creating the subset, the user can classify the selected

part of the bone by choosing an identifier out of a list (see Figure 2 [c]). This step is

similar to the one used in a tagging system when the user connects data content with

computer-readable semantic information (tags). Classification is mainly used (a) as

additional information for the fitting algorithm and (b) to provide a subordinated

calculation of the characteristic features of the bone being examined.

Table 1 shows a

selection of the characteristic features of a bone that can be extracted using the fitted

sq-model. To do this, component classification is necessary. In the context of surgical

support, it is of paramount importance that the system to be able to calculate those

values automatically in order to eliminate the time overhead otherwise required for

user interaction and to use mathematical models to verify accuracy. The quality of the

result depends on the correct classification of every part of a given bone in the model,

so that the system selects the appropriate parameter set to determine the features of

the bone at hand.

4.3 Combination of Data Decomposition and Classification

Fig. 5 shows the combination of the manual data decomposition and classification

operation by offering a basic bone model to the user. If the point cloud is segmented

from MRI images of a leg, for example, the user has to choose the standard model of

a leg. The same is true for every other bone in the human body (see Fig. 1). The clas-

sifications of all parts of the bone, like the femur head (Fig. 5), are previously con-

nected to the single SQ in the standard model.

After loading the standard model, the user matches each SQ of the standard model

to the point cloud by adjusting the parameters using the described tool (see section

4.1). In this way, data decomposition as well as component classification is combined

in a unique step without changing interaction tools or paradigms.

Fig. 5. One-step solution: an example of the data decomposition step for the femur.

5 Results

For testing the implementation, the decomposition and fitting procedures have been

performed on five sets of intact lower-limb bone data, each taken from a human pro-

band using MRI imaging. Each set consists of a hip bone and its two attached femoral

bones. Additional validation has been performed using two sets of pig bones of the

same type. Both selection tool models have been implemented and tested with the

patient data as input. Due to space constrains we only list the results of two exem-

plary components, although the remaining result does not significantly differ. The

first represents a human pelvis bone, the second an attached femoral bone. As can be

seen, the absolute error between the manual and semi-automatic approaches is only a

few millimeters or even less, meaning that the result comes close to established clini-

cal standards while saving time that might otherwise be spent on user-interaction.

Errors are mainly caused by ambiguities resulting from certain extreme-points lying

in comparatively flat surface areas where the SQ model’s approach would choose

differently from the intuitive approach, yet quantitatively correctly. A fully automated

test was also conducted; however, the results included components that were far from

their actual position.

Table 2. Results from semi-automatic sq-fitting (femur, left, positions / lengths in m, directions

as vector).

Feature Manual method SQ-Method

Axis

(org / dir)

(-0,143, -0.358, -0,312)

(0.1395 -0.9901 0.0068)

(-0.1494, -0.3614, -0.3112)

0.1495, -0.988, 0.0364

Head center (-0,158 -0.12 -0.295) (-0.1584, -0.1226, -0.2985)

Head diameter 0.044 0.0422

G.Trochanter tip

position

(-0.184, -0.133 -0.347) (-0.1812, -0.13 -0.341)

Knee axis

(org / dir)

(-0.14, -0.565, -0.298)

(0.1013, 0.9948, 0.0001)

(-0.138, -0.57, -0.301)

(0.08, 0.9967, 0.0006)

Table 3. Results from semi-automatic sq-fitting (pelvis, positions and lengths in m, directions

as vector).

Feature Manual method SQ-Method

HJC

(left, right)

(-0.158 -0.12, -0.295)

(-0.168, -0.131, -0.113)

(-0.158, -0.123, -0.298

(-0.167, -0.132, -0.110

ASIS pos.

(left, right)

(-0.094, -0.06, -0.31)

(-0.104, -0.066, -0.088)

(-0.096, -0.054, -0.306

(-0.106, -0.051, -0.082

PSIS pos.

(left, right)

(-0.221, -0.051, -0.279)

(-0.229, -0.052, -0.132)

(-0.22, -0.051, -0.268

(-0.222 -0.055 -0.133

Pelvis origin (-0.168, -0.131, -0.113) (-0.167, -0.132, -0.110

Pelvis

orientation

),,( zyx

(0.999, 0.004, 0.0445)

(0.0034, 0.9999, -0.013)

(0.0445, 0.0134, 0.9989)

(0.9989, 0.004, 0.0445)

(-0.0034, 0.9999, -0.013)

(-0.0445, 0.0133, 0.9989)

6 Conclusions

In this paper, we have presented a prototype for an interactive system that supports

the surgeon in the sophisticated task of reconstructing a realistic model of the human

skeletal system from 3D point data. Our technique was based on presenting the user

with a powerful and efficient model to steer the reconstruction, classification and

manipulation process of the algorithms. It embeds the model into an easily accessible

tool that provides important information as desired to achieve an optimal result. Due

to the efficiency of the sq-model and the vast possibilities of parallelization, which

are discussed in [4], these techniques are suitable for real-time applications. Tables 2

and 3 show the first results using this approach in comparison with the “analogue” or

“by-hand” process used during surgery planning today.

Several enhancements to the existing approach are planned. First, more analytic

descriptions of a larger amount of limb components are needed to provide the user

with as many templates as possible for the bone component classification task. In the

longer term, it is planned to provide a model of the whole lower limb structure of the

human body. Furthermore, the geometric models will be improved to allow for cap-

turing finer topological details that result in an even more exact approximation of the

bones’ surfaces. For this, the components of the sq-formula, especially those that

influence overall curvature, will be brought to a more abstract level and, at the same

time, be replaced by smooth interpolating functions. Finally, the selection tool will be

improved in compliance with the additional capabilities of the enhanced models.

References

1. Barr, A.H., 1981. Superquadrics and angle-preserving transformations. IEEE computer

graphics and applications, 1:1, pp. 11–23.

2. Banégas, F., Jaeger, M., Michelucci, D.. Roelens, M., 2001. The ellipsoidal skeleton in

medical applications. In Proceedings of the sixth ACM symposium on solid modeling and

applications, ACM Press, pp. 30–38.

3. Chevalier, L., Jaillet, F., Baskurt, A., 2003. Segmentation and superquadric modeling of 3D

objects. In Journal of Winter School of Computer Graphics, WSCG'03, 11:2, Feb. 2003, pp.

232–239.

4. Cuypers, R., Tang, Z. Luther, W., & Pauli, J., 2008. Efficient and Accurate Femur Recon-

struction using Model-based Segmentation and Superquadric Shapes. Proceedings Tele-

health and Assistive Technologies ~ TeleHealth/AT 2008 - Editor(s): R. Merrell, R.A. Coo-

per 4/16/2008 - 4/18/2008 Baltimore USA, ACTA Press 2008

5. Goldfinger, E., 1991 Human anatomy for artists: The Elements of form, Oxford University

Press, New York.

6. Jaklič, A., Leonardis, A., Solina, F., 2000. Segmentation and recovery of superquadrics. In

Vol. 20 of Computational Imaging and Vision, Kluwer, Dordrecht.

7. Kecskeméthy, A., 1999. MOBILE Version 1.3. User’s Guide

8. Kršek P., Krupa P., 2003. Human tissue geometrical modelling, In: Applied Simulation and

Modeling, Calgary, CA, IASTED, 2003, pp. 357-362, ISBN 0-88986-384-9

9. Kurazume, R., Nakamura, K., Okada, T., Sato, Y., Sugano, N., Koyama, T., Iwashita, Y.,

Hasegawa, T., 2007. 3D reconstruction of a femoral shape using a parametric model and

two 2D fluoroscopic images. IEEE International Conference on Robotics and Automation,

pp.3002-3008, 2007

10. Muraki, S., 1991. Volumetric shape description of range data using "blobby model", Com-

puter graphics, 25:4, July 1991, pp. 227–235.

11. Marlow, C., Naaman, M., Boyd, D., Davis, M., 2006. HT06, tagging paper, taxonomy,

Flickr, academic article, to read. In HYPERTEXT ’06: Proceedings of the seventeenth con-

ference on hypertext and hypermedia, pp. 31–40, ACM, New York, USA.

12. Martin, T., Cohen, E., and Kirby, M, 2008. Volumetric parameterization and trivariate B-

spline fitting using harmonic functions. In Proceedings of the 2008 ACM Symposium on

Solid and Physical Modeling (Stony Brook, New York, June 02 - 04, 2008). SPM '08.

ACM, New York, NY, pp. 269-280.

13. Metaxas, D., DeCarlo, D., 1998. Shape evolution with structural and topological changes

using blending. IEEE transactions. Pattern recognition and machine intelligence, 20:11,

Nov. 1998, pp. 1186–1205.

14. Peng, X., Chi, X., Ochoa, J.A., Leu, M. C., 2003. Bone surgery simulation with virtual

reality. ASME DETC2003/CIE, Chicago USA, September 2-6 2003.

15. Solina, F., Bajcsy, R., 1990. Recovery of parametric models from range images: The case

for superquadrics with global deformations. IEEE transactions on pattern analysis and ma-

chine intelligence 12, pp. 131–147.

16. Terzopoulos, D., Metaxas, D., 1991. Dynamic 3D models with local and global deforma-

tions: Deformable superquadrics. In Transactions on pattern analysis and machine intelli-

gence, 13: 7, July 1991, pp. 703–71.

17. Werneke, J., 1994. The Inventor Toolmaker: Extending Open Inventor. Addison Wesley

Pub Co Inc.2

Edition.

18. Zheng, G., Dong, X., Rajamani, K.T., Xuan Zhang; Styner, M., Thoranaghatte, R.U.,

Nolte, L.-P., Ballester, M.A.G., 2007. Accurate and Robust Reconstruction of a Surface

Model of the Proximal Femur From Sparse-Point Data and a Dense-Point Distribution

Model for Surgical Navigation. Biomedical Engineering, IEEE Transactions on , vol.54,

no.12, pp.2109-2122,.

19. Zhou, L., Kambhamettu, C., 1999. Extending superquadrics with exponent functions:

Modeling and reconstruction. In CVPR99, pp. II: 73-78.