
Basic Definitions and Operations for Gestalt Algebra
Eckart Michaelsen and Jochen Meidow
FGAN-FOM, Gutleuthausstrasse 1, 76275 Ettlingen, Germany
Abstract. The gestalt algebra is a mathematical construction designed to cap-
ture the perceptual structure of complex patterns. Such patterns occur e.g. in
aerial images of urban terrain. The principles of gestalt construction – namely
proximity, good continuation, similarity and symmetry – are used in a recursive
way to describe image or scene data using terms following an algebraic defini-
tion. Such description can be used for recognition, matching, or data mining.
1 Introduction
In particular in the automation of understanding remotely sensed data – such as aerial
images of urban terrain – frequently unexpected structures occur. ‘Unexpected’ here
means that such structures or even similar structures are not present in the training
data set available for the automatic understanding algorithms. Conventional pattern
recognition methods are doomed to fail in such situations with the closed world as-
sumption – whereas human experts (and even non-expert subjects) perform reasona-
ble in understanding such unexpected patterns.
In this contribution we will not attempt to describe an implemented computer sys-
tem mimicking such human skills. Instead, we will try to outline a mathematical de-
scription language for pattern structure. This will follow the findings of perceptual
psychology – namely the gestaltists’ view on human perception. Hence it is called
gestalt algebra.
Our hope is that – once this language has been precisely defined and its properties
and possible meanings are understood – it may foster the development of algorithms
and in the end automatic systems that can cope with these unexpected pattern struc-
tures and reach the human performance.
2 Related Work
This is interdisciplinary work. Our own work is in image understanding in particular
of remotely sensed data. It is however inspired by work from perceptual psychology
as well as from algebraic and syntactic approaches to pattern recognition.
Michaelsen E. and Meidow J. (2009).
Basic Definitions and Operations for Gestalt Algebra.
In Proceedings of the 2nd International Workshop on Image Mining Theory and Applications, pages 53-62
DOI: 10.5220/0001961400530062
Copyright
c
SciTePress

Gestaltism. Gestaltist literature (e.g. [15] and [5]) often argues by drawing dot pat-
terns demonstrating the gestalt phenomena by use of the reader’s/observer’s own
perceptive mechanisms. In order to include such psychological findings in machine
vision attempts have been made to lay mathematical – i.e. statistical – foundations to
them [6,1]. There are approaches that combine such gestalt elements with generative
grammars into a theory of vision for machines, animals, and humans [2].
Practical Attempts on Remote Sensing Data. The main interest in automatic under-
standing of previously unseen repetitive or symmetric gestalts comes from remote
sensing – in particular from aerial image analysis of urban scenery. Very interesting
early work on arrangements and hierarchies of arrangements of objects in aerial im-
ages has benn presented already in 1980 by Nagao and Matsuyama [12]. The
SIGMA-system [8] was designed to instantiate explicitly modeled gestalts with pro-
duction rules. Examples were rows of houses along a road. Sophisticated control
structures are proposed to cope with handling the inevitable large computational ef-
fort.
Algebraic Methods in Pattern Recognition. Visual language theory as for instance
presented in [7] uses generative syntactic structures (on images instead of strings).
There is also a branch along this line that uses algebraic settings [13]. This is known
as image algebra. Much of that work is related to the pixel grid structure of images,
e.g. how convolution filters or morphological filters can be captured algebraically etc.
There is an algebraic theory of pattern recognition algorithms given by Zhuravlev
[16]. Derived from that the descriptive image algebra has been introduced along with
descriptive image models [3,4]. There the search for regularities of arbitrary form and
hierarchy is identified as one of the many objectives of image analysis inside the
descriptive algebraic approach. Also symmetry groups and grid structures used in this
contribution are particular allowable transforms in the image formation models used
in descriptive image algebra theory. However, in our gestalt algebra such group trans-
forms are always understood locally with respect to a specific location (and direc-
tion).
Own Previous Work. The idea of gestalt algebra has been introduced in [10]. How-
ever, this rather preliminary work lacks some of the precision required for such an
endeavor. Particularly, the definitions there rested on just a metric space. According-
ly, the definitions of the primitive operations were too vague. Here we emphasize that
the operations must be well-defined. The new gestalt resulting from an operation is
given by error minimization calculation algorithms. So we have to show existence
and uniqueness of this solution. In order to do so, we restrict ourselves here to loca-
tions in a vector space with directions, since this is a structure of the primitive domain
of practical relevance. Examples are ‘edgels’ in 2D or surface patches in 3D. More
general definitions may follow in future work.
Most of our own previous work is about specifically designed productions systems
describing particular structures. E.g. production systems utilizing specific gestalt
groupings were proposed e.g. for complex 3D-scene understanding [14] and building
recognition from high resolution SAR-images [10]. [11] treats the mitigation of the
54

computational load for such systems. An approximating and accumulating interpreter
is given. The purpose of this contribution is a generalization of all such systems: The
revealing of their common fundament in perceptual grouping.
3 Definitions
The gestalt algebra is introduced in four steps: In Section 3.1 the domain with its
primitive elements is introduced. Then the symmetry groups are given in Section 3.2.
They are working on the associated space – such that the objects can be mapped on
each other. These mappings define a matching assessment for groups of objects. Thus
the fundament is laid for the gestalt operations given in Section 3.3 and finally our
new algebra in Section 3.4.
3.1 The Primitive Domain and its Gestalts
Let V be a vector space of finite dimension n over the field R. We also demand that
there is a metric d
V
given on V, e.g. the Euclidean metric. We identify the column
vector v=(v
1
,…, v
n
)
T
with its homogenous notation v=(v
1
,…, v
n
,1)
T
.
Furthermore, let P be the corresponding projective space, i.e. R
n+1
\{0} with the
usual equivalence x~λx for geometric entities and λ≠0. We also demand that there is
a projective metric d
P
given on P, e.g. the Hilbert projective metric.
We call the following subset D of the product space
{}
=∈×⋅=(, ) ; 0DvpVPpv
(1)
the primitive domain. On it we will build our algebraic structure. Examples are edge
elements (edgels) with location and direction - which may be obtained by a gradient
filter - or spatial positions with a local surface orientation. The constraint in (1) de-
mands that the locations v are located on the hyperplane p.
In order to distinguish more than one type of object we introduce a finite set of
primitive symbols S
p
={
σ
1
,…,
σ
s
}. A trivial metric d
S
can be defined on this finite set
being zero for equal elements and one otherwise.
Furthermore, each object has a quality assessment value 0
≤
α
≤
1 assigned to it. α=1
refers to the quality of the best possible object
1
. α=0 refers to the quality of the worst
possible object. I.e. these are the least salient objects, those that just trespass the thre-
shold used for segmentation.
Such an object instance g={
σ
j
, d, α} will be called a primitive gestalt henceforth
where d
∈
D are the feature values of it. For such primitive gestalts a metric is intro-
duced by choosing suitable positive weights ß.
()
σασ αβσσβ β
=++
111 1 2 22 2 12 12 12
( ,( , ), ),( ,( , ), ) ( , ) ( , ) ( , )
SS VV VV
dvp vp d dvv dpp
(2)
1
“best” may refer to the largest occurring value in the particular image or to the largest possible value given a
synthetic optimal datum such as an ideal edge
55

3.2 Operations on Primitives - Proximity and Symmetry on the Domain
Here the primitive gestalt operations are defined. We also give some important stan-
dard examples. Generalization to non-primitive operations will be given in Section
3.3.
Definition 1. Gestalt Operations on Primitive Gestalts. A symmetry group is group
G of mappings f such that
→:fV V
(3)
is bijective and preserves the metric.
G contains the identity as neutral element and an
inverse
f
-1
for each element.
Such mappings have a reference frame associated with them – i.e. a position
γ
p
∈
V,
an orientation
γ
o
∈
P, and a scale factor
γ
s
∈
R. Let d
0
,…,d
k
be a tupel of vectors in D
with
k<m. We further demand that the minimization problem
γ
ε
=
=−
∑
2
0
1
min ( ( ))
k
ii
i
dfd
(4)
is uniquely solvable. From such a solution we can obtain a new assessment using
ςε
α
−⋅
<
=≤01e
,
(5)
with a suitable domain-dependent parameter ζ. So we have defined an operation
o
G
which constructs a new gestalt object from the
k primitive gestalts in a unique way.
We write
1
( ,..., )
Gk
od d
or also
12G
do d
if k=2.
(6)
For each exemplary Gestalt operation we have to show separately that the operation is
well-defined (existence and uniqueness of the solution) and list corresponding alge-
braic laws – such as existence of a neutral element, associativity, commutativity etc.
Example 1. The gestalt principle ‘proximity’ is defined on a finite set of points
X by
∈
=
∑
1
||
xX
cx
X
and
ς
α
−−
∈
=
∑
2
()
1
||
xc
xX
e
X
.
(7)
The new cluster gestalt object contains
c as position attribute and α as assessment.
It can also contain a direction from the eigenspace
s corresponding to the larger ei-
genvalue of the covariance. Note here the scaling parameter ζ which is discussed in
Section 4. We write
{
}
α
=
==⊕
1
,( , ),
k
new i i
gtcs g
(8)
where
t is a simple tree consisting of the symbol ‘cluster’ at the root and the symbols
σ
j
at the leaves. The corresponding symmetry group is the trivial group containing
only the identity. Averaging gives always a well-defined result in metric vector spac-
es. It is associative and commutative.
56

However, such proximity grouping can also be done in the projective space P in-
stead of the vector space
V. Then it represents the gestalt principle good continuation.
Averaging can then be defined using the metric on
P. For this gestalt operation a new
symbol is needed. We use ‘¦’. There may be a problem with well-definedness. For
certain uniformly arranged configurations there will be no center in
P. This can be
fixed by introducing an arbitrary ‘worst possible’ gestalt with assessment value zero.
‘¦’ is commutative and it will also turn out associative once the operation on non-
primitives is given in Section 3.3.
Example 2. Mirror symmetry on the 2D vector space over real numbers as indicated
in Figure 1a). A mapping
f of this space is defined by an axis
2
in normal form
a=(a
1
,a
2
,a
3
). We write line equations as row vectors and points as column vectors
using homogeneous coordinates. For 2D points
x=(x
1
,x
2
,1)
T
with the incidence rela-
tion
a·x=0 we will have x’=f(x)=x. For all other points x’=f(x)≠x will hold. Fixing for
them
x
3
=1 and |a|=1 we determine x’ by the mirror constraint a·x’= - a·x and the
perpendicular constraint
a·(x×x’) =0 on the axis and the join. These conditions are
sufficient to calculate
x’ given x and a (or a given x and x’). Furthermore we can
obtain as location
y=a×(x×x’)
for the new symmetry gestalt object. These are analytic
linear calculations that have a unique solution. We write
{
}
==,( , ),1 | ´
new
gtyagg
(9)
where
t is a simple tree consisting of the symbol ‘mirror’ at the root and the symbols
σ
and
σ
´ the leaves.
However, if an object has not only a position
x
∈
V but also a direction d
∈
P as indi-
cated in Fig. 1a) the corresponding direction will be
d’=x’×(a×d). The simultaneous
solution for location and direction will be over determined. Here there will be an error
sum
ε≥0 and this value will be used to assess the new mirror gestalt object, cf. equa-
tion (4).
For simplicity, we have used the cross product here which restricts the definition to
the 2D domain. However, generalization to
nD is straight forward. The operation is
well-defined and commutative, but it will turn out being not associative (once the
operation on non-primitives is given in Section 3.3).
Example 3. Rotational symmetry of order
m on the 2D vector space over real num-
bers. A mapping
f of this space is defined by the invariant center point c=f(c), i.e. the
fix point. Here we will use Euclidean coordinates. For a 2D point
x=(x
1
,x
2
)
T
a set of
m points {x, x’, …,x
(m-1)
} is generated:
ββ
ββ
⎛⎞
=+ −
⎜⎟
−
⎝⎠
()
cos( ) sin( )
()
sin( ) cos( )
i
ii
x
cxc
ii
where β=2π/m
(10)
This set represents the new gestalt object. It is attributed with the center
c, the order
m and the vector (x-c) which gives its size and phase. Given a sub-set X of the points
{x, x’, …,x
(m-1)
} not all points must be present – the parameters c and r=|x-c| can be
2
we do not discuss a mirror at infinity here, i.e. a
1
=a
2
=0
57
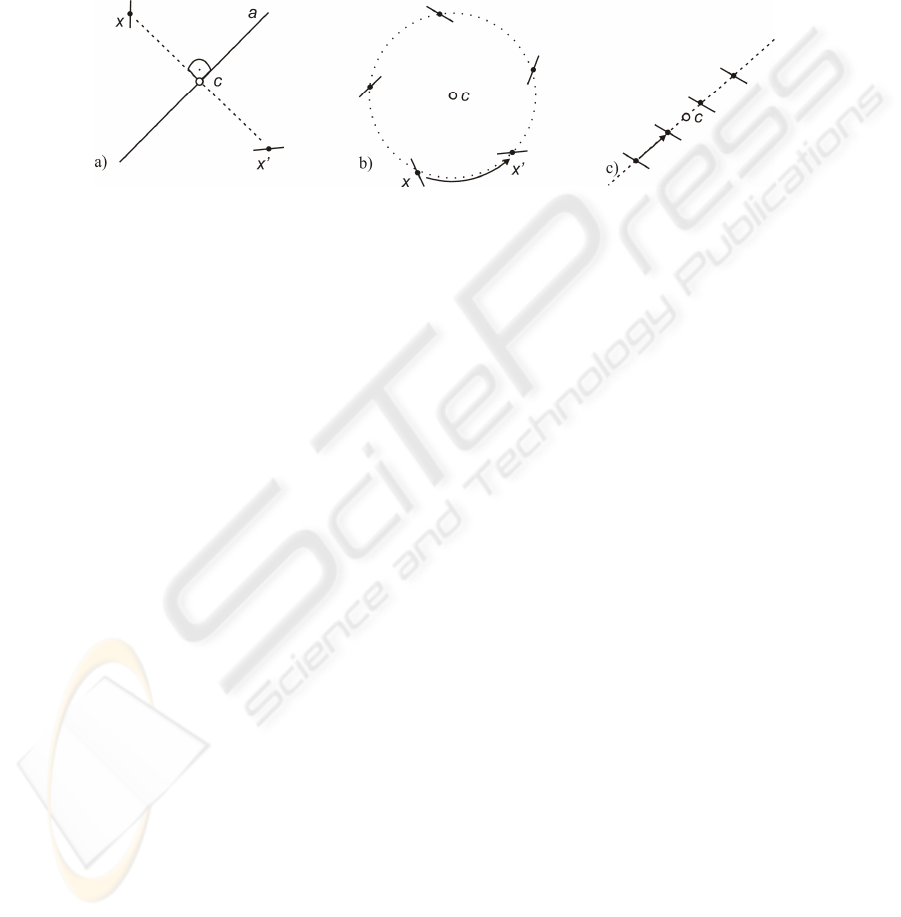
obtained by minimizing the squared error sum. For this there is an analytic solution –
so the operation is well defined.
c and (x-c) are the attributes of the new gestalt ob-
ject. Figure 1b) shows an almost perfect example with
m=5. We write
{
}
α
=
=−=:
1
,( ,( )),
k
new i i
gtcxc g
(11)
where
t is a simple tree consisting of the symbol ‘rotation
5
’ at the root and the sym-
bols
σ
j
at the leaves. This operation will turn out non-associative as well.
Fig. 1. Symmetries in the domain: a) mirror symmetry, b) rotational symmetry, c) lattice.
Example 4. One dimensional lattice structure on the 2D vector space over real num-
bers is given by a translation vector
v. Using ordinary Euclidean coordinates a point x
is mapped to
x’=x+v. This mapping generates an infinite simple group. Therefore
such a gestalt object can never be completely present in a finite measurement datum –
such as an aerial image. But given a sub-set
X of the points {…,x, x’, …} the vector v
can be estimated uniquely from minimizing the sum of squared errors, cf. Figure 1c).
This again gives a well-defined operation and we will write
{
}
α
•
•=
==
()
1
,( , ),
ki
new i
gtcv g
(12)
where
t is a simple tree consisting of the symbol ‘lattice’ at the root and the symbols
σ
j
at the leaves. For this operation we have commutativity – because v is a projective
entity where the sign does not matter. Associativity will also be given once we have
defined the operation also on non-primitive gestalts in Section 3.3.
3.3 Operations on Non-primitives Gestalts
The idea now is that each of the gestalts presented in Fig. 1 is scaled down and then
composes new non-primitive gestalts: E.g. a lattice of rotational groups that consist of
mirror symmetric pairs of cluster objects. The algebraic formulation allows writing
down arbitrary complex non-primitive gestalts as a term. The basic structure of such
terms is a derivation tree.
Definition 2: Gestalt Derivation Tree. A gestalt algebra derivation tree is a tree of
gestalt objects that codes the algebraic decomposition of the gestalt at the root. At the
leaves of such trees we have primitive gestalts and at each other node we have a non-
primitive, i.e. a gestalt operation and attributes (at least a location and often orienta-
tion and scale as well). We will call a sub-tree of a such a tree a root-sub-tree if it has
58
common root with the tree.
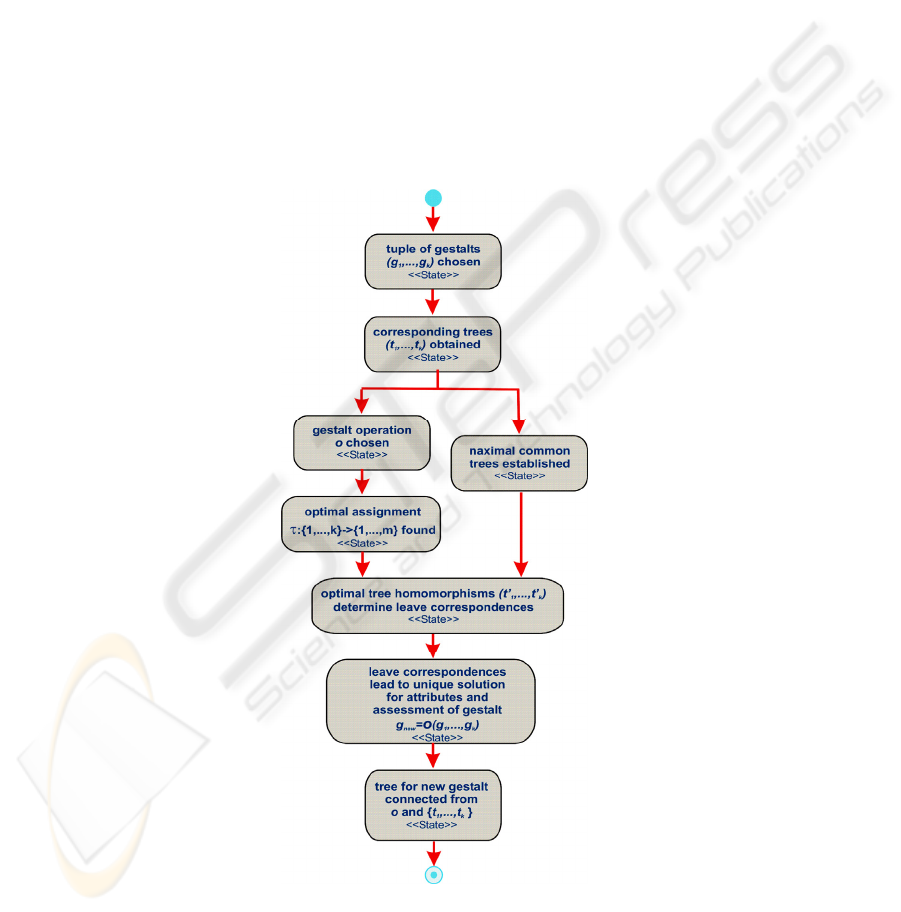
Definition 3. Non-primitive Gestalt Algebra Operation. Given a tuple of gestalts
(g
1
,…,g
k
) to which this operation is to be applied the first thing to do is accessing the
corresponding trees
(t
1
,…,t
k
). The diagram in Figure 2 shows that then two things can
be done in parallel:
1) Establish
t
max
which is the maximal tree for which tree homomorphism can be
achieved to a root sub-tree of all
t
i
. Tree homomorphism here means the structure of
the tree must be equal and the operations at the non-terminal nodes as well. We refer
to corresponding root-sup-trees as
(t’
1
,…,t’
k
). There may be several homomorph pos-
sibilities for each.
2) Chose the gestalt operation o i.e. the group G and the mappings as given in the
examples 1-4 in Section 3.2. Recall that
k≤m must hold, where m is the cardinality of
G. Given this a correspondence τ is determined such that the error is minimal follow-
ing equation (2). Recall, this is a primitive step like in Section 3.2.
Fig. 2. State diagram for gestalt algebra operation.
59

Once these two steps have been done among the homomorph possibilities for the
(t’
1
,…,t’
k
) the optimal correspondence is searched. Given these correspondences the
optimization (2) can be done in the same primitive manner – yielding a residual error
and the position, direction etc. for the new more complex gestalt.
Fig. 3. Example of a non-primitive gestalt: a) primitives with location and orientation, b) non-
primitive gestalt – lattice of rotational groups of mirror symmetries
Figure 3 shows an example. It is a two element lattice whose location and orientation
is indicated in Figure 3b) as white dot with crossing line indicating the orientation. Its
two parts are indicated as light grey dots. These consist each of five mirror gestalts in
darker grey. Each of them is given by the small primitives. We will write it as
{
}
(
)
•
•= =
==:
2 5 () ()
11
,( , ),1 ( | ')
ii
example i j j j
gtcv gg
.
(13)
60

Here all trees are completely present and homomorph. Moreover, the deviations from
the set-positions are zero giving this gestalt (13) an assessment of one. In practice
some of the parts will be missing, the given ones will be displaced by measurement
errors or morphing, and there will be spurious clutter primitives (and non-primitives).
So
α=1 will be very rare.
The closure of these operations given the set of primitives defined in Section 3.1
will be called a gestalt algebra. An element of such algebra codes a set of primitive
objects and a chain of operations on them that explain their arrangement in the do-
main. We emphasize that the Examples 1-4 are only standard examples for operations
particularly suited for gestalt perception in 2D image space. In particular for spaces of
higher dimension – such as spatial data, videos, or music – other group operations
may also induce valuable gestalt operations. For each such particular group the alge-
braic properties of the corresponding gestalt algebra operation must be invested sepa-
rately – e.g. by giving a counter example against associativity or proving it. And the
interaction with the other gestalt algebra operations must be revealed (i.e. searching
for distributivity).
4 Conclusions, Discussion and Outlook
An algebraic structure has been defined that can capture complex perceptive gestalt
structure of patterns in mathematical terms. Associativity, distributivity, and commu-
tativity for the operations are certainly still open issues in this field. Non-primitive
gestalt objects may be decomposed in a different sequence of operations – as is evi-
dent from the example in Fig. 2. The tree homomorphism required for matching in
Section 3.3 has to include such equivalences. In future work we will attempt giving a
clear definition of these associativity, distributivity, and commutativity laws which
gestalt algebra inherits from the group structure inside the operation definitions.
It will be advisory to derive the assessment functions and scale parameters ζ (see
Equation (5)) inside the gestalt operations from probability models for foreground
objects and clutter density estimations or defaults. Such modeling can be done either
by estimating the parameters using the probabilities directly or giving bounds for
them by using expectation values following [1]. For the time being this remains an
open research topic. From Figure 3 it is obvious that each step in a gestalt algebra
term is associated with certain `change in scale´. We also leave that issue to future
work.
Also a major issue will be the computational complexity. Using gestalt algebra top
down to generate gestalts is probably not really a big computational load – however
using it bottom up to mine given sensor data for structure will cause considerable
effort. Recall that the structure of these definitions is of quite combinatorial nature
and we assume that such search will be NP-hard. There are, however, ideas for miti-
gating these troubles by trading soundness for feasibility [9, 11].
61

Acknowledgements
We thank Dr: Michael Holicki from LFK GmbH, Unterschleißheim, Germany, for
particular hints and constructive criticism.
References
1. Desolneux A., Moisan L., Morel J.-M.: From Gestalt Theory to Image Analysis. Springer,
Berlin (2008)
2. Guo, C.-E., Zhu, S.C., Wu, Y. N.: Modelling Visual Patterns by Integrating Descriptive
and Generative Methods. IJCV, 53 (1), (2003) 5-29
3. Gurevich, I. B.: The Descriptive Framework for an Image Recognition Problem. in Proc. of
the 6th Scandinavian Conference on Image Analysis I (Pattern Recognition Society, Fin-
land, 1989), Vol. 1, pp. (1989) 220–227
4. Gurevich, I. B., Yashina V. V.: Descriptive Approach to Image Analysis: Image Models //
Pattern Recognition and Image Analysis: Advances in Mathematical Theory and Applica-
tions. - MAIK "Nauka/Interperiodica"/Pleiades Publishing, Inc., - Vol.18, No.4. (2008)
518-541
5. Kanisza, G.: Grammatica del Vedere. Il Mulino, Bologna (1980)
6. Lowe, D.: Perceptual Organization and Visual Recognition, Kluwer Academic Publishers,
Boston (1985)
7. Marroitt, K., Meyer, B. (eds.): Visual Language Theory. Springer, Berlin (1998)
8. Matsuyama, T., Hwang, V. S.-S.: Sigma - a Knowledge-based Image Understanding Sys-
tem. Plenum Press, New York (1990)
9. Michaelsen E., Soergel U., Thoennessen U.: Perceptual Grouping in Automatic Detection
of Man-Made Structure in high resolution SAR data. Pattern Recognition Letters.27 (4),
(2006) 218-225
10. Michaelsen E., Arens M., Doktorski L.: Elements of a Gestalt Algebra: Steps towards
Understanding Images and Scenes. In: Gurevich I., Niemann H., Salvetti O. (eds.): Image
Mining and Applications, workshop proceedings of IMTA in conjunction with
VISIGRAPP 2008, Insticc Press, Portugal, (2008) 65-73
11. Michaelsen E., Doktorski L., Arens M.: Shortcuts in Production Systems – A Way to In-
clude Clustering in Structural Pattern Recognition. Proceedings of PRIA-9-2008, Lo-
bachevski State Univ., Nizhni Novgorod, Vol. 2, (2008), 30-38
12. Nagao, M., Matsuyama T.: A Structural Analysis of Complex Aerial Photographs, Plenum
Press. New York (1980)
13. Ritter, G. X., Wilson, J. N.: Handbook of Computer Vision Algorithms in Image Algebra.
CRC Press, New York (1996)
14. Stilla U., Michaelsen E.: Semantic modelling of man-made objects by production nets. In:
Gruen A, Baltsavias EP, Henricsson O (eds) Automatic extraction of man-made objects
fromaerial and space images (II). Birkhäuser Verlag, Basel (1997) 43-52
15. Wertheimer, M.: Untersuchungen zur Lehre der Gestalt, II. Psychologische Forschung, 4
(1923) 301-350
16. Zhuravlev, Yu. I.: An Algebraic Approach to Recognition or Classification Problems.
Pattern Recognition and Image Analysis, 8(1) (1998) 59–100
62
