
A CHAOS BASED ENCRYPTION METHOD USING
DYNAMICAL SYSTEMS WITH STRANGE ATTRACTORS
Arash Sheikholeslam
Department of electrical engineering, Isfahan University of Technology, Isfahan, Iran
Keywords: Lorenz system, Dynamical system, Strange attractor, Dynamical cipher block.
Abstract: In this paper, one approach for using dynamical systems with strange attractors as cipher system is
introduced. The necessity of Synchronization for this type of system is discussed in depth and an applicable
chaotic encryption-decryption system, some of which is specialized for image cryptography, is developed.
The developed system is based on a discrete modification of the Lorenz dynamical system. Synchronization
features and spatial and spectral properties of the system are obtained experimentally.
1 INTRODUCTION
Many block cipher encryption methods are in use,
among them are: EBC, CBC, NDS, CFB and OFB
(Menezes, 1997) and (Beker, 1982); block cipher
methods are also common in the field of image and
speech cryptography. The method which will be
developed in this text uses dynamical systems with
strange attractors to map an image in to a ciphertext.
Image can be defined in its traditional form.
Definition: Image is defined as a 2-D discrete
function , with the range of [0-255], where the
amplitude of is the intensity of the pixels of the
image (Gonzalez, 2002).
Unpredictable behavior of deterministic systems
has been called chaos. The word "Chaos" was
introduced by Tien-Yien Li and James A. Yorke in a
1975 paper entitled "Period Three Implies Chaos"
(Li, 1975).The term "strange attractors," first
appeared in print in a 1971 paper entitled "On the
Nature of Turbulence"( Ruelle, 1971).Some people
prefer the term "chaotic attractor" . (Sprott, 1993)
Many dynamical systems does not have a unique
point or set of points as their attractor but rather a
complicated geometrical object which according to
(Sprott, 1993) is called strange attractor. A more
precise definition of strange attractor is included
here.
Definition: If an attractor for a dissipative
system has a noninteger dimension, then the
attractor is a strange attractor of that system.
Among the features of strange attractor with
respect to (Hilborn, 2000), is the ability of
trajectories to remain within some bounded region
by intertwining and wrapping around each other (not
intersecting) and without repeating themselves. The
geometry associated with these attractors makes
them capable of generating pseudo random
sequences, the noise like features of which can be
used for cryptography. The dependence of the
systems with strange attractors to the initial
conditions makes them less predictable and therefore
more reliable for our purpose. But it increases the
need for a precise synchronization between the
encryption and decryption systems.
The next section is concerned with the design
procedure of the cipher system. Section 3 introduces
an applicable cipher system based on the theory of
section 2. The applicability of the system is shown
through some experiments in section 4.
2 DESIGN STEPS
According to (Menezes, 1997) a block cipher is
defined as below.
Definition: An n-bit block cipher is a function
E: Vn ×K → Vn, such that for each key K K,
E(P,K) is an invertible mapping (the encryption
function for K) from Vn to Vn, written EK(P). The
inverse mapping is the decryption function, denoted
DK(C). C = EK(P) denotes that ciphertext C results
from encrypting plaintext P under K.
259
Sheikholeslam A. (2009).
A CHAOS BASED ENCRYPTION METHOD USING DYNAMICAL SYSTEMS WITH STRANGE ATTRACTORS.
In Proceedings of the International Conference on Security and Cryptography, pages 259-265
DOI: 10.5220/0002105402590265
Copyright
c
SciTePress
In this work the blocks are different from the
above definition, where blocks are defined as n*m-
byte matrices instead of n-bit blocks. A block cipher
whose block size n is too small may be vulnerable to
attacks based on statistical analysis (Menezes,
1997), as a consequence of this study we will use
large blocks with large keys. Specialization of the
system for image cryptography encourages us to
take the size of our block as large as the size of
normal images.
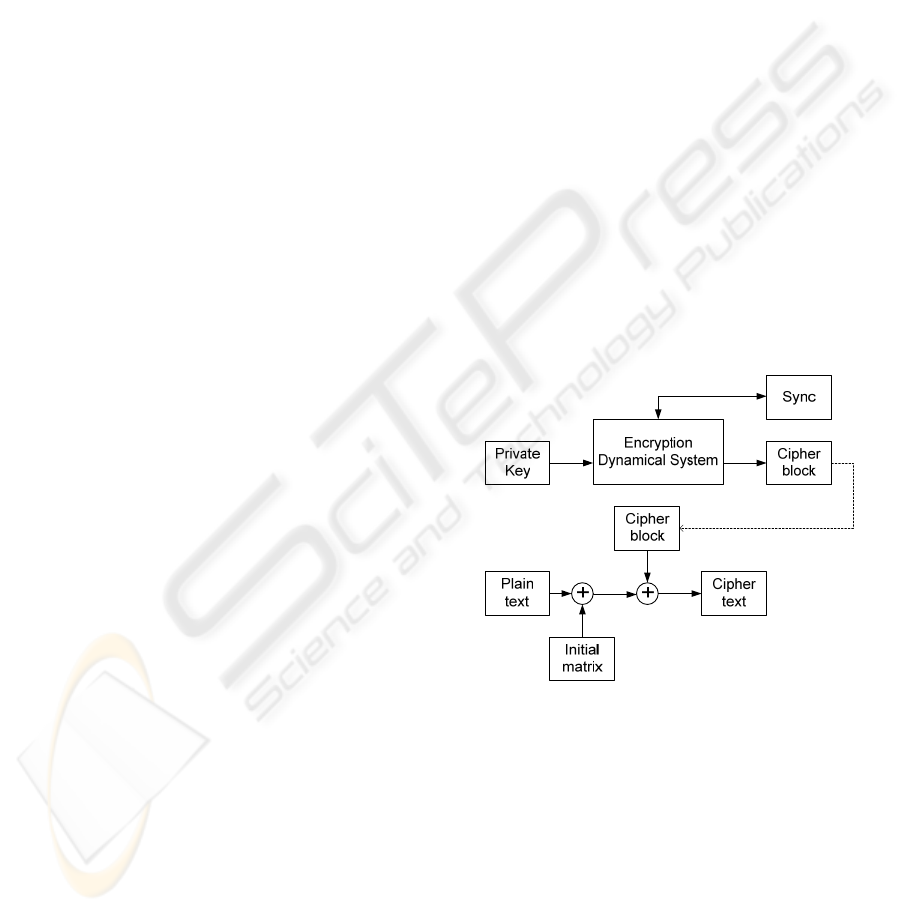
The overall system scheme can be observed in
Figure 1 and Figure 2 where the
Encryption/Decryption Dynamical system is a
dynamical system with strange attractor which
means it is a state space differential/difference
equation, that has at least three dimensions (three
state variables).(Hilborn, 2000) One of the state
variables can be used for developing the Cipher
block matrix (Figure 1 and 2), while one other state
variable will be updated at every iteration under the
influence of the private key (this process will be
discussed in detail). For a dynamical system of the
form
, if
is the variable
that chosen to develop the Cipher block matrix and
if we start the generation of Cipher block at some
time N then:
,
1
(1)
Where p*q is the size of the block and k is a time
step parameter. Needless to mention that a
transformation ::, is necessary in
the process of Cipher block matrix because this
matrix should take part in XOR operation.
There are two phases in encryption-decryption
process. First the synchronization phase in which
the Encryption system generates a synchronization
key (sync) and decryption system updates its initial
condition in accordance with the synchronization
key. The synchronization key can be a dynamical
public key or it can be sent out via a secure channel.
The second phase is the encryption/decryption under
the influence of the private key.
After every execution of the second phase, the
initial conditions of the state equations will be
changed and therefore the generated Cipher blocks
will be completely different from each other using a
constant private key.
As introduced by Pecora and Carrol in (Pecora,
1990) two dynamical systems can be synchronized
in certain conditions. The aim of synchronization in
our work is to enforce two equal dynamical systems
(with different initial conditions) to generate the
same Cipher block matrices in both of the
Encryption/Decryption dynamical systems.
It can be shown that two identical chaotic
systems can be synchronized if they are coupled
together in an appropriate way (Stavroulakis, 2006),
that is to decompose a chaotic system in to two
subsystems (Stavroulakis, 2006). An n-dimensional
chaotic system with state-space equation
can be decomposed in to two subsystems
, (k-dimensional) and , (m-
dimensional) where . Now to drive a
response system with an equation the same as
( ′
,′), we calculate the variable from
, and substitute it in the response system,
taking
′
,
,
,
, for small
and
is the Jacobian of subsystem. For
synchronization to happen
need to go toward
zero and therefore the lyapunov exponents must be
negative. Although the above conditions are derived
for continues dynamical systems, experiments and
simulations show that they are applied to the discrete
modification of Lorenz system which will be
introduced in the next section.
Figure 1: Cipher system (Encryption).
Synchronization in our case occurs in an offline
form, which is to generate a synchronization key by
the Encryption Dynamical system (Sync in Figure 1)
and then the Cipher block will be generated. Using
the synchronization key, The Decryption system can
update itself to the initial conditions of the
Encryption system before generating the Cipher
block.
SECRYPT 2009 - International Conference on Security and Cryptography
260
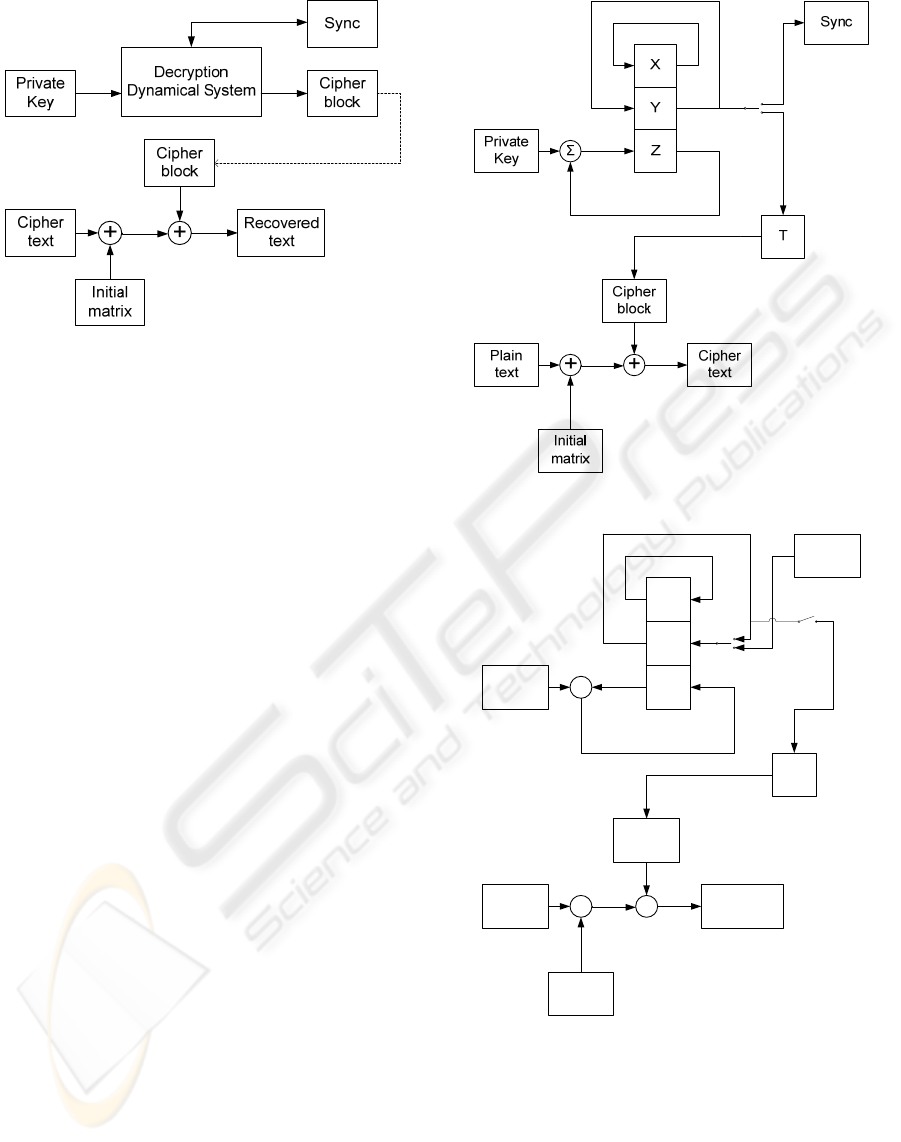
Figure 2: Cipher system (decryption).
3 LORENZ CIPHER SYSTEM
In this work Lorenz dynamical system was used as
Encryption/Decryption system (Figures 3 and 4).
The original Lorenz dynamical system (
Lorenz, 1963)
is a continuous dynamical system with state
equations:
(2)
(3)
(4)
,
10 8 3
⁄
28.
A modified discrete version of Lorenz system is
defined here with a difference equation of the form:
1
(5)
1
(6)
1
(7)
,10 8 3
⁄
28 0.01.
A new parameter is introduced above which is the
length of time step. This parameter should be taken
carefully not to destabilize the system. While taking
smaller than 0.02 observed to work well, a precise
discussion of stability with respect to is beyond
the scope of our work. The discretized Lorenz
system allows faster computations in cipher system.
The result for running these equations (without
taking a private key in to account) for 10000
iterations is plotted in Figure 5. X, Y, Z are plotted
against discrete time (10003000) in Figures
6, 7 and 8.
Figure 3: Cipher system (Encryption).
Figure 4: Cipher system (Decryption).
In this work state variable Y was chosen for filling
the Cipher block matrix and transform fits the
range and quantizes the generated numbers. T(Y) -Z
is plotted in Figure 9. (No key was used here).
+
Private
Key
Cipher
text
Initial
matrix
+
Recovered
text
Cipher
block
X
Y
ZΣ
T
Sync
A CHAOS BASED ENCRYPTION METHOD USING DYNAMICAL SYSTEMS WITH STRANGE ATTRACTORS
261
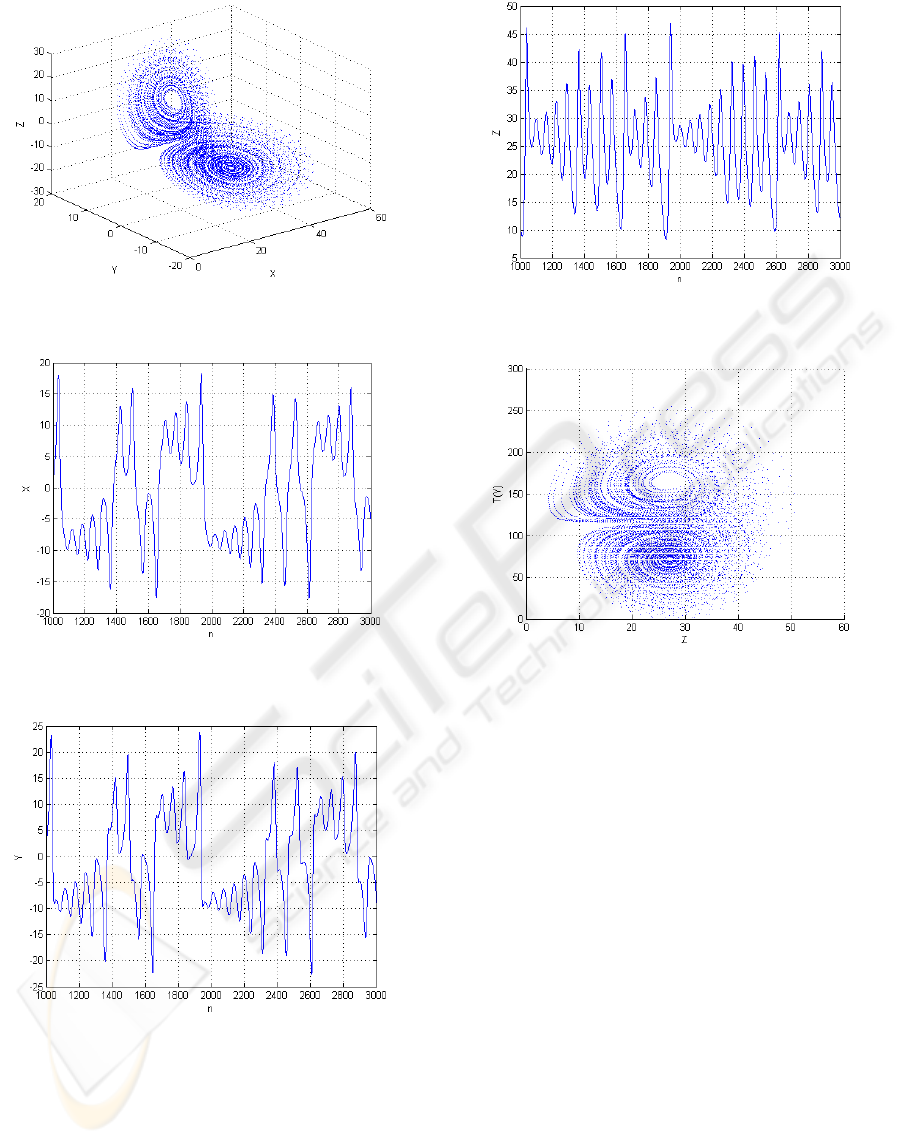
Figure 5: result of running space equations (5), (6) and (7)
for 10000 iterations.
Figure 6: Observation of X(n) for running space equations
(5), (6) and (7) for n, from 1000 to 3000.
Figure 7: Observation of Y(n) for running space equations
(5), (6) and (7) for n, from 1000 to 3000.
For testing the synchronization condition on this
system we break it into two subsystems:
And
Figure 8: Observation of Z(n) for running space equations
(5), (6) and (7) for n, from 1000 to 3000.
Figure 9: plot of T(Y(n)) against Z(n) for n from 0 to
10000.
Assuming two Lorenz systems with different initial
conditions:
0
(8)
and
′
′
. The Eigen values of the
Jacobian are also the transverse lyapunov exponents
(
Stavroulakis, 2006) and are:
,
.
Which are negative and therefore the two systems
synchronize as ∞ for almost every initial
condition. In the next section it is experimentally
shown that two coupled modified Lorenz systems
synchronize within a few time steps (a short length
synchronization key).
4 EXPERIMENTS
Based on what was derived in the above sections, we
evaluate our system which is based on our modified
SECRYPT 2009 - International Conference on Security and Cryptography
262
Lorenz dynamical system. The value of in
equations (5), (6) and (7) was taken to be 0.02. The
initial conditions for the Encryption system were
chosen as
0
10,
0
7,
0
35 these
values were chosen because they are about the
center of the Lorenz attractor Figure 5.
For generating the Cipher block, this form of
equation (1)
was used:
,50
(9)
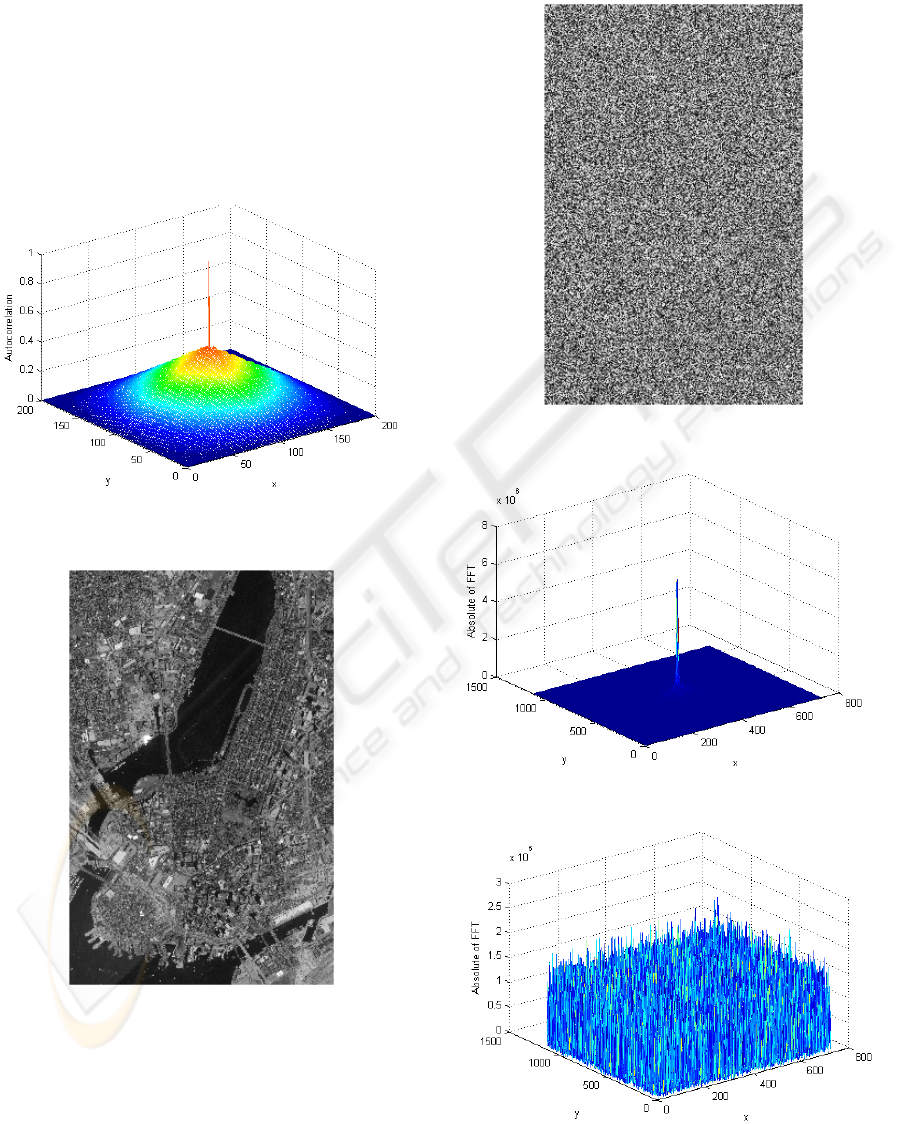
The autocorrelation of a Cipher block of size 100*100 is
calculated and depicted in Figure 10. (No key was used).
Figure 10: The autocorrelation of a Cipher block of size
100*100.
Figure 11: Original image (which was taken from the math
work increments,”Matlab R2007A”).
Figures 11 and 12 show the original image
(which is a satellite picture of Boston that was taken
from Math work increments, Matlab R2007A)
and the encrypted image. The 2D-FFT of original
and encrypted images is plotted in figures 13 and 14.
The histograms of the plain text and Cipher text can
be observed in figures 15 and 16.
Figure 12: Encrypted image.
Figure 13: FFT of original image.
Figure 14: FFT of encrypted image.
A CHAOS BASED ENCRYPTION METHOD USING DYNAMICAL SYSTEMS WITH STRANGE ATTRACTORS
263
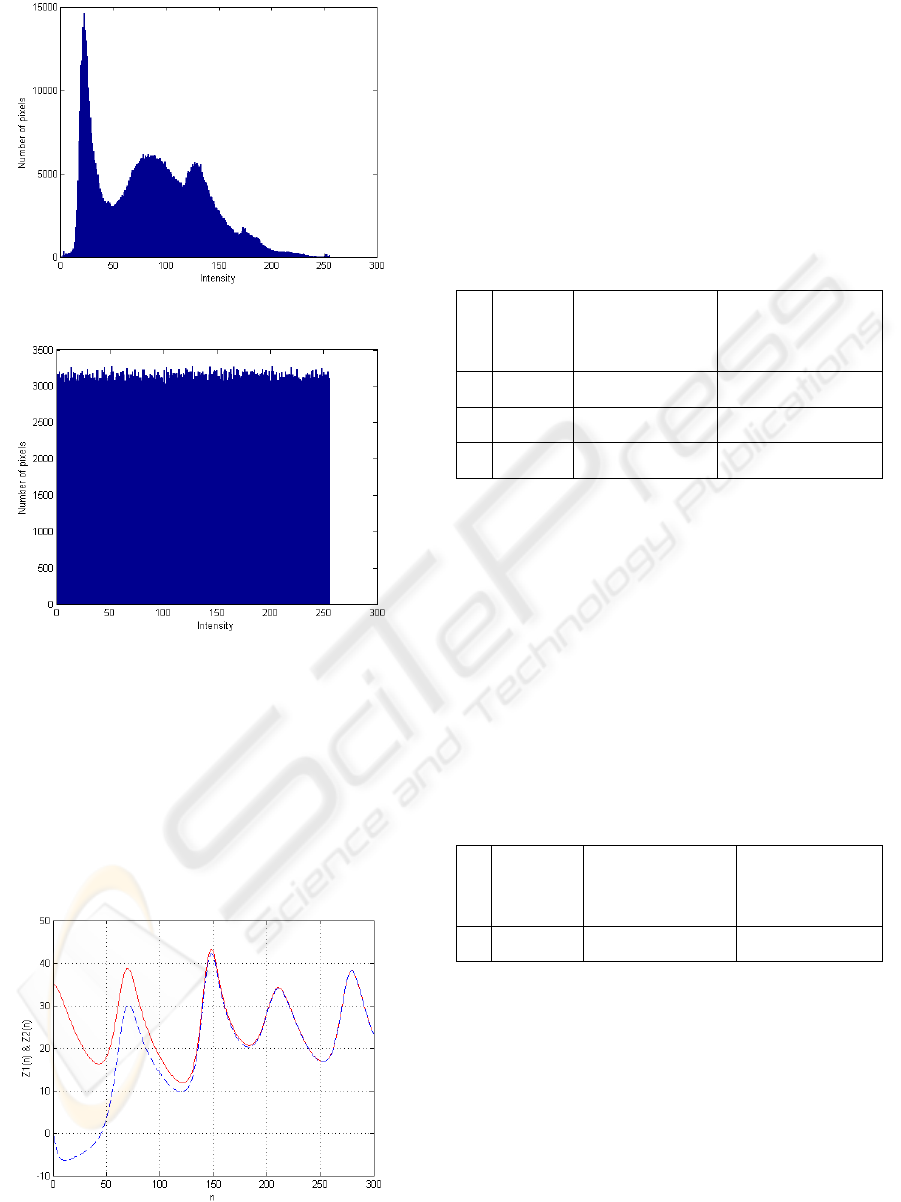
Figure 15: Histograms of the plain text.
Figure 16: Histograms of the Cipher text.
The results of our experiments (Figure 17 and
Table1) ensure us about the rapid synchronization of
two coupled modified Lorenz systems even when
they are started from very different initial
conditions. In Figure 17 the Encryption system
initial conditions are x1,y1,z110,7,35
and the Decryption system initial conditions are
x2,y2,z227,70,0 .n is the length of
synchronization key.
Figure 17: Rapid synchronization of Encryption and
Decryption systems.
A sum of square error is calculated to compare the
original and decrypted images.
∑
(10)
(10)
Where is the number of pixels;
and
are the
original and decrypted image pixel intensity values.
Table 1 shows the mean square error values for
different initial conditions after synchronization
process with a synchronization key of length 300.
Table 1: Square Error of decryption after synchronization
(with different initial conditions).
Encryption
initial conditions
(x,y,z)
Decryption
initial conditions
(x,y,z)
1 0.00000 (-10,-7,35) (-10,-7,35)
2 0.00000 (-10,-7,35) (0,0,0)
3 0.00000 (-10,-7,35) (9000,350,15000)
The above results make us sure that for almost
every practical initial condition for the decryption
and encryption system, a synchronization key of
length 300 will enforce the decryption system
toward the encryption system’s initial condition. For
a better insight to the geometry of the system
another is calculated but without any
synchronization taking in to account and the initial
condition of the decryption system is slightly
changed (Table 2). This Observation briefly shows
the dependence of the system to the initial
conditions.
Table 2: Square Error of decryption without
synchronization.
Encryption initial
conditions (x,y,z)
Decryption
initial conditions
(x,y,z)
4 17234526 (-10,-7,35) (-10,-7,.35.1)
5 CONCLUSIONS
Benefited from the complexity and unpredictability,
chaotic pseudorandom sequences generated by the
nonlinear dynamical systems with strange attractors
show excellent capabilities for cryptography. The
Lorenz attractor used in this work was chosen
because it is simple, and a large body of research is
available about its dynamics. It is possible to use
higher dimensional chaotic systems and higher
SECRYPT 2009 - International Conference on Security and Cryptography
264

number of keys.
As shown in this paper, two dynamical systems
that have the same strange attractor can be
synchronized and used as Cipher system. The spatial
and spectral features of the system that were
obtained experimentally, ensures us that the system
is truly applicable. The dependence of the system on
the initial conditions increases the system
independence from the plain text.
Unpredictability, complexity and dependence of
the systems output on the initial condition make this
system desired for applications such as military
image cryptography.
ACKNOWLEDGEMENTS
The author wishes to thank Prof. Moddares
Hashemi, Isfahan University of Technology, for his
help and support.
REFERENCES
Alfred J. Menezes, Paul C. van Oorschot, Scott A.
Vanstone “Handbook of Applied Cryptography”, CRC
Press, Inc., USA, 1997
N. Lorenz, "Deterministic non--periodic flow," J. Atmos.
Sci., vol. 20, pp. 130-140, 1963
Julien C. Sprott “Strange Attractors Creating Patterns In
Chaos”, 1993
T. Li and J. Yorke, Period three implies chaos. American
Mathematical Monthly, vol. 82, 985-992, 1975
D. Ruelle, F. Takens “On the nature of turbulence”,
Commun. Math. Phys, vol. 20, pp. 167-192, 1971
Peter Stavroulakis.”CHAOS APPLICATIONS IN
TELECOMMUNICATION”, CRC press, 2006
Pecora, L.M. and Caroll, T.L., Synchronization in chaotic
systems, Phys. Rev. Lett.,vol. 64, 821–824, 1990.
Mustafa R.S. Kulenovic, Orlando Merino, “Discrete
Dynamical Systems and Equations with
Mathematica”, Chapman & Hall/CRC, 2002
Orfanidis, S.J., “Optimum Signal Processing.An
Introduction. 2nd Edition”, Prentice-Hall, Englewood
Cliffs,NJ, 1996.
Henry Beker, Fred Piper,”CIPHER SYSTEMS the
protection of communications”,Northwood
publications,1982
L. Arnold and V wihstutz ”Lyapunov Exponents (lecture
notes in mathematics)” Springer-verlog, 1984
Rafael C. Gonzalez, Richard E. Woods “Digital image
processing” Prentice-Hall, 2002
Robert C. Hilborn “Chaos and Nonlinear Dynamics An
introduction for scientists and engineers second
edition” Oxford university press 2000
A CHAOS BASED ENCRYPTION METHOD USING DYNAMICAL SYSTEMS WITH STRANGE ATTRACTORS
265
