Road-Following and Traffic Analysis using

High-Resolution Remote Sensing Imagery

Seyed Mostafa Mousavi Kahaki

, Mahmood Fathy

and Mohsen Ganj

Computer Eng. Department

Islamic Azad University Dezful Branch, Iran

Associate Professor Computer Eng. Department

Iran University of Science & Technology, Iran

Computer Eng. Department

Islamic Azad University Shoshtar Branch, Iran

Abstract. As vehicle population increases, ITS (Intelligent Transportation Sys-

tems) becomes more significant and mandatory in today’s overpopulated world.

Vital problems in transportation such as mobility and safety of transportation

are considered more, especially in metropolitans and road ways. Road traffic

monitoring aims at the acquisition and analysis of traffic figures, such as pres-

ence and numbers of vehicles, and automatic driver warning systems are devel-

oped mainly for localization and safety purposes. In this paper we propose a

strategy for road following from aerial images. Real time extraction and locali-

zation of a road from an aerial image is an emerging research area that can be

applied to vision-based traffic controlling and navigation of unmanned air ve-

hicles. In order to deal with the high complexity of this type of images, we in-

tegrate detailed knowledge about roads using explicitly formulated scale-

dependent models. The intensity images are used for the extraction of road

from aerial images. Threshold techniques, Hough transform and learning algo-

rithm are used for the road extraction and car detection. The results show that

the proposed approach has a good detection performance.

1 Introduction

Today satellite and airborne remote sensing systems can provide large volumes of

data that are invaluable in monitoring Earth resources and the effects of human activi-

ties. Traffic control is an emerging research topic due to rapidly increasing interest in

their use. Currently, traffic control is a difficult and time consuming task that need too

several human operators. Traffic controlling on satellite image can save time and

costs. The urban traffic control process is accomplished through cameras which are

installed in highways, in current technology. Recently, with considering aerial image-

ries, existence of an Intelligence road Extraction and car detection system which be

able to control the road traffic would have more remarkable performance, Investiga-

tions about road Extraction and car detection in aerial imageries Involved in informa-

Mousavi Kahaki S., Fathy M. and Ganj M. (2009).

Road-Following and Trafﬁc Analysis using High-Resolution Remote Sensing Imagery.

In Proceedings of the 3rd International Workshop on Intelligent Vehicle Controls & Intelligent Transportation Systems, pages 133-142

 SciTePress

tion and data related to GIS and this maintained data needs to become up to date in

every certain period of time. Road Extraction and Car detection in aerial Imageries is

a modern Controversy issue in computer vision science that has also some influences

on many other projects and operations. This paper proposed an integrated approach

for automatic road extraction from remotely sensed imagery by combining digital

image processing, remote sensing and Geographic Information System (GIS) tech-

nologies, Since the launch of new optical satellite systems like IKONOS, Quick Bird

and Geoeye-1, this kind of imagery is available with 0.4 - 1.0 meter resolution. Ve-

hicles can be observed clearly on these high resolution satellite images. Results show

that the proposed algorithm has a good detection performance. Some vehicle detec-

tion methods have been studied using aerial imagery[1][7][9]. The Major factors that

effect essentially on our subject are: the number of different objects in Imagery,

amount of relationship between them and some properties that distinguish them from

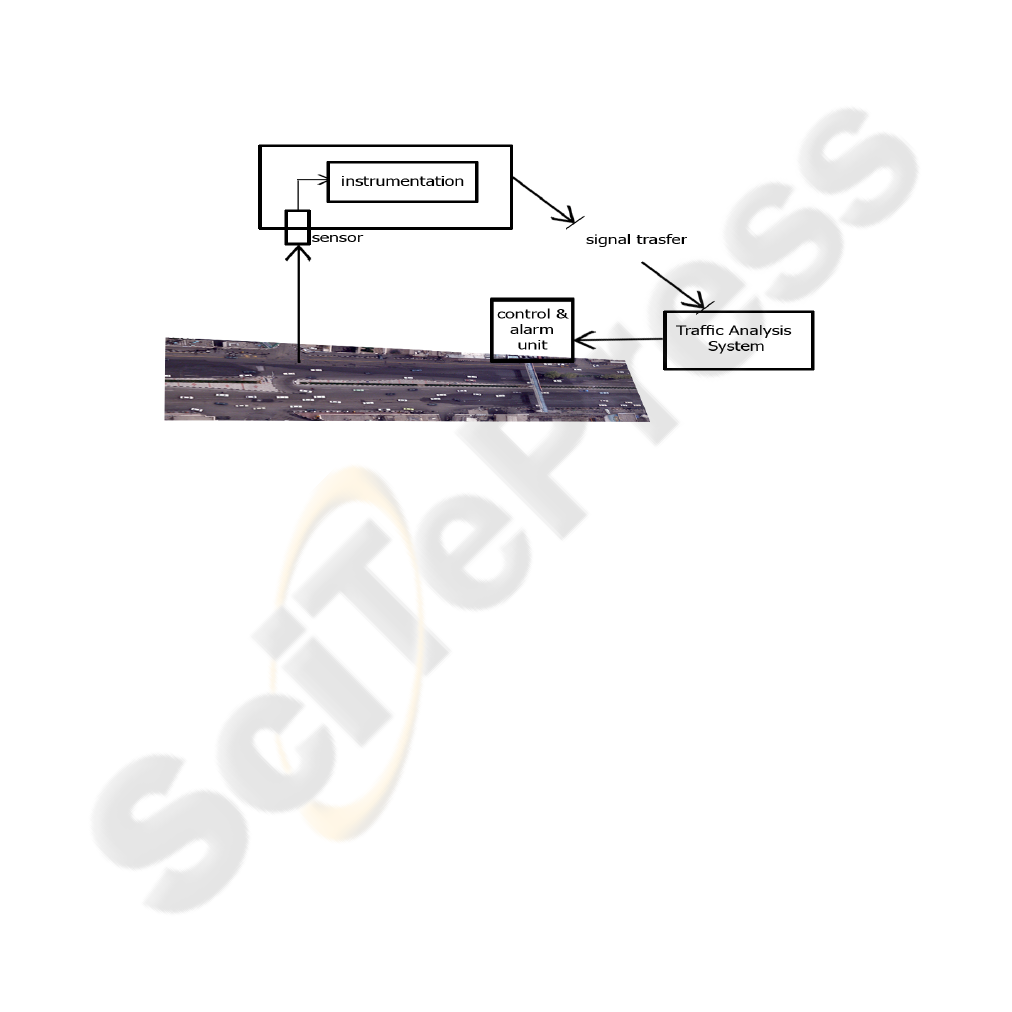
other objects. Example system for traffic monitoring has shown in Figure 1.

Fig. 1. Example system for traffic monitoring (Azadi Avenue, Tehran-IRAN).

Before explaining any detail, we scan other parts of this article:

Sect.2: Important Issues in road Extraction and car detection process.

Sect.3: Main idea and road and car, essential items and their characteristics.

Sect.4: An execution on aerial Imageries, advantages and disadvantages.

Sect.5: A proposal about works for future on this topic.

2 Related Works

Vehicle detection and road extraction has been receiving attention in the computer

vision. A number of conventional express way incident detection algorithms have

been developed in the recent years[11][12]. Techniques based on morphology and

neural network for vehicle detection and road extraction had developed in machine

vision, but only a few researches have investigated the detection of traffic sensing on

aerial images[13][14]. In this paper we used high resolution images from Geoeye-1

satellite. This imagery are taken full color and in equal interval from the ground.

Geoeye-1 is equipped with the most sophisticated technology ever used in a commer-

134

cial satellite system. It offers unprecedented spatial resolution by simultaneously

acquiring 0.41-meter panchromatic and 1.65-meter multispectral imagery. The used

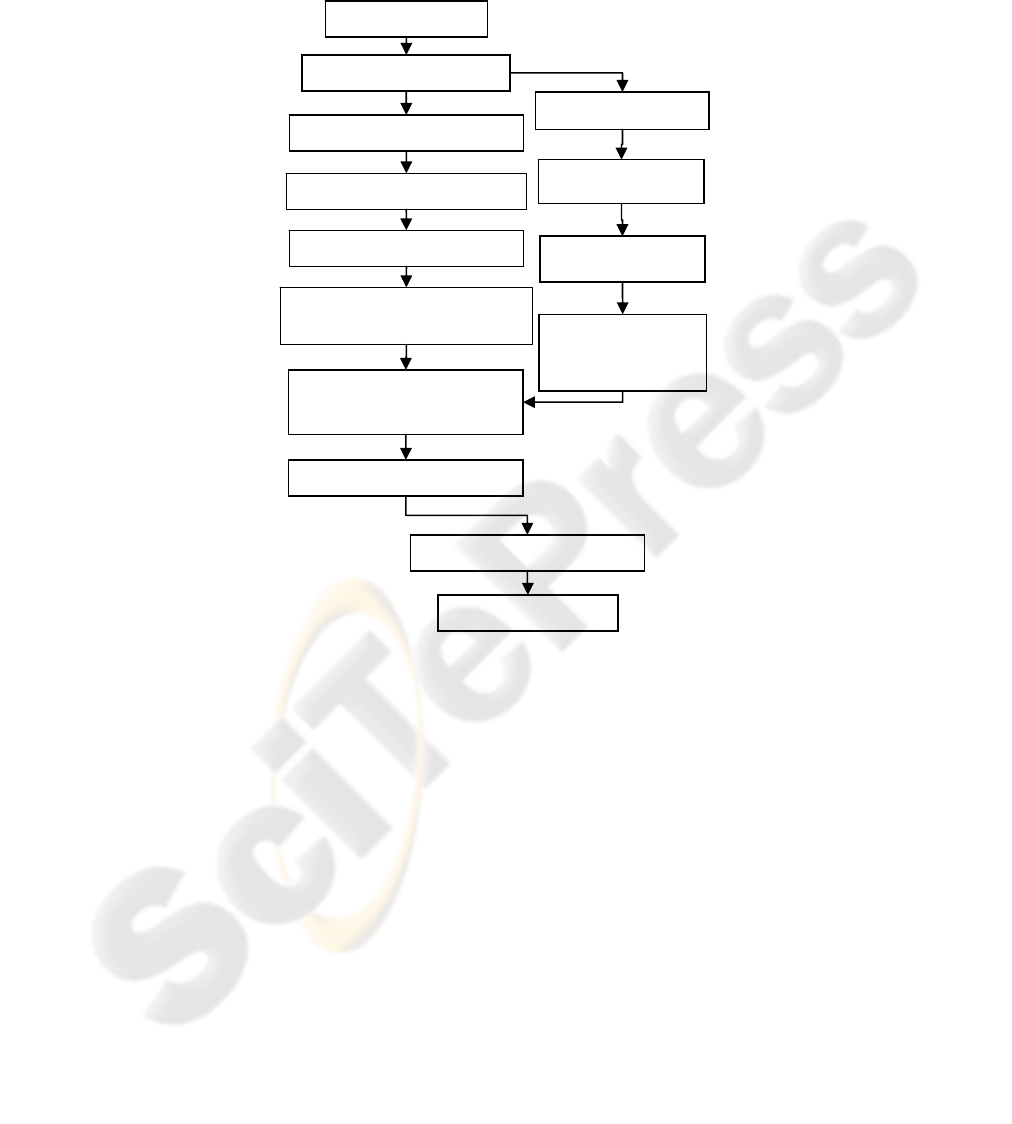
method is presented on figure 2 as a flowchart:

Fig. 2. Flowchart of the traffic analysis algorithm.

3 Vehicle Detection and Road Extraction Approach

First, we must extract the roads and distinguish coordinates of these roads's district;

the car detection's operation is accomplished. In addition, we need feature extraction

of car and road because other detection of road's district, only those objects can stu-

died that are in the road district. This is really useful to know that roads are presented

as a direct district with a different color in the aerial imageries. Therefore, linear fea-

ture can be an appropriate feature in detection at road's district, as you can see in

Figure 3(a). Another feature which roads possess, Is the lines that exist in white color

in all the roods and they are considered as a proper feature in detection operation.

These lines are available continuously along side the road and discontinuously in the

middle of the road. The other feature that used in this method is the color of the road,

ut Ima

Threshold

Ima

e Enhancement

Binar

Ima

Mor

holo

Transfor

Learnin

orith

Table Pixel Whose Is Greater

Than Given Threshol

Morphological

post-processing

Count Vehicle

Traffic Anal

sis

Results

Edge Detection

Hough Transform

Out put Road

Extraction Results

135

which completely distinguishes between road and other parts. With threshold opera-

tion, we can separate road and background from each other and preparing imagery for

other operations. This color threshold can be approached with mean of colors at the

roods in several aerial imageries that are available in dataset. After threshold, edge

detection operation can be run better. We had used the method for edge detection.

This method has higher performance rather than the others. You will see the result in

figure 3(d). In digital imageries, in those points that there is edge on them, there are

differences of color too. Therefore, sharpen operation leads to increase the difference

at color in edges and it can enhance the image classification. So, next operation like

edge detection can be executed with higher precision.

In recent years the Hough transform and the related Radon transform have re-

ceived much attention. These two transforms are able to transform two dimensional

images with lines into a domain of possible line parameters, where each line in the

image will give a peak positioned at the corresponding line parameters. This has lead

to many line detection applications within image processing, computer vision. In the

last step, we use Hough transform and Radon transform for distinguished road and

direction detection for road following in aerial images as shown in figure 3 (d). We

extract the edge lines angle to find direction of road. Several definitions of the Radon

transform exists, but they are related, and a very popular form expresses lines in the

form ρ = x cos θ + y sin θ, where θ is the angle and ρ the smallest distance to the

origin of the coordinate system. As shown in the two following definitions (which are

identical), the Radon transform for a set of parameters (ρ, θ) is the line integral

through the image g(x, y), where the line is positioned corresponding to the value of

(ρ, θ). The δ ( ) is the delta function which is infinite for argument 0 and zero for all

other arguments (it integrates to one).

∫∫

+∞

∞−

+∞

∞−

= dy)dx siny - cos x - (p y) g(x,),(

θθδθ

(1)

Or the identical expression

∫

+∞

∞−

+= )ds cos s sin p , sin s - cos g(p),(

θθθθθ

(2)

In his Ph.D. thesis [10], Peter Toft investigated the relationship of Radon transform

with the Hough transform, and it is shown that the Radon transform and the Hough

transform are related but not the same. The Radon transform of a function f(x,y) is

defined as the integral along a straight line defined by its distance P from the origin

and its angle of inclination θ

, a definition very close to that of the Hough transform

and requires a lot of processing power in order to be able to do its work in a reasona-

bly finite time. Now a day high processing power is not a problem. Here we are con-

sidering all the line has same skew angle and the range of angle is -45

to 45

. Here

Radon transform will detect the angle from the upper envelope. If the skewed angle is

more than 45

or less then -45

the upper envelope may contain 2 lines in different

directions. An example is shown in Figure 3(d) having 20 degree of skewed angle.

136

(a)

(b)

(c)

(d)

Fig. 3. Road Extraction (a) An original image (b) The Threshold pre-processing result (c) The

Edge detection pre-processing result (d) The Road Extraction result and direction.

After road extraction and finding orientation of road, we need to detect the cars in

the road. This trend is moved simply because only those objects can be handled that

are inside the road. One of the important textures of cars, which helps us to detect, is

car model. We can detect a car with using its model from dataset examples by using

neural network classification.

137

(a)

(b)

Fig. 4. (a) An original image (b) The morphology pre-processing result.

The dataset examples for car detection has extracted as shown in figure 5.

Fig. 5. Dataset examples.

After road extraction, cars should be counted for traffic analysis. Cars always in

aerial imageries are appearing in rectangular shape as you can see in figure 4(b).

Morphological Gradient use to enhance vehicle features. It is defined by Gradient:

G (f) = (f ⊕ g) − (f Θ g)

Where g is a structuring element, f is a gray scale source image, f ⊕ g means dila-

tion operation, and f Θ g means erosion operation.

Figure 4 shows an original image of Tehran-Karaj highway and its morphology

Gradient processing result. This process can use to discriminate vehicle targets and

non-vehicle targets. Figure 5 shows some dataset examples for neural network classi-

fication. One noticeable feature in aerial imageries is the color of the cars that has a

significant difference with other objects. This phenomenon can help us to detect the

cars by adaptive threshold processing and the results of threshold simulation indicate

that this method has high performance. After classification with neural network me-

thod the cars should be counted for traffic analysis. After counting cars, we can de-

termine the amount of traffic in roads. Since all the aerial imageries are take from a

fixed interval, the amount of road traffic with considering the cars number in one

certain district is determined by adaptive threshold.

138

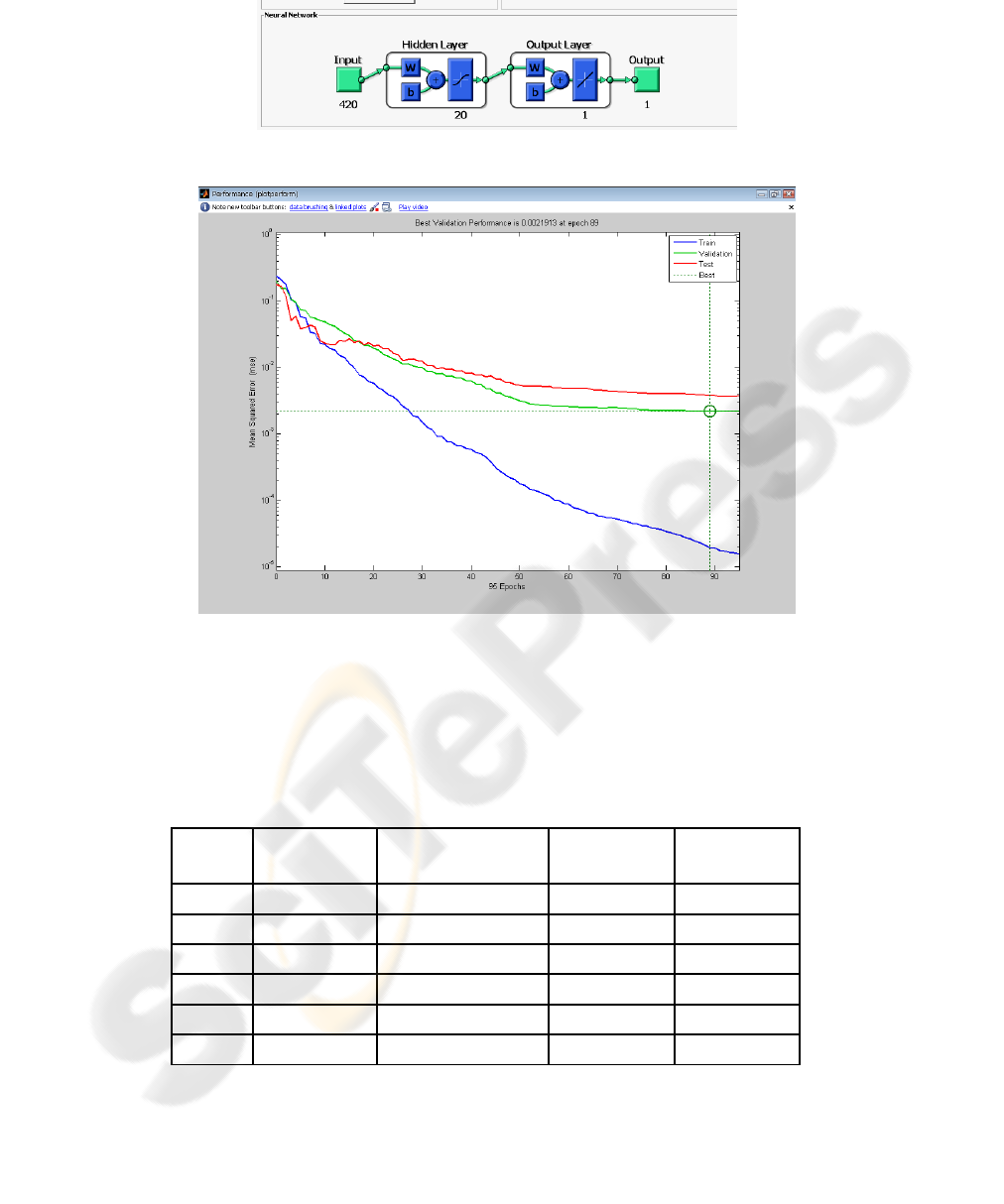
Fig. 6. Combining input information as neural network's input parameters.

Fig. 7. Mean Square Error for Learning System.

This scheme, of course, has some disadvantages: its performance is about 90% and

it can not detect the cars out side the road. This scheme can accelerate to transfer the

information to drivers who are intended to cross a road and it also can help the police

to traffic control. You can see the performance table of car detection in road at table1.

Table 1. Vehicle detection results.

Site Number of cars

Number of detected

cars

Number of

undetected cars

Performance

Road1 8 7 1 87.5%

Road2 52 47 5 90.3%

Road3 31 24 7 77.41%

Road4 30 27 3 90.3%

Road5 19 17 2 89.5%

Road6 55 44 11 80%

139

After car detection and count cars, we can extract number of cars on a certain part of

road and can analysis the traffic on it as shown in figure 9.

Fig. 9. Counting cars and simple traffic analysis

4 Conclusions

In this paper, we focus on the issue of vehicle detection and road extraction from high

resolution satellite imagery for traffic analysis. Further work could include more

training samples for neural network classification, and fusing more information like

edge shapes to improve the correct detection rate. And also can detect an accident

from high resolution satellite images. Imageries are taken by satellites and special

planes at the moment. We can control the road's traffic via a traffic balloon. Traffic

balloons are more flexibility to apply: There is possibility to pursue the roads via

traffic balloon as auto pilot. Another capability of this intelligence system is to follow

the deviant cars which have illegal speed.

References

1. Hong, Z. & Li, L.: Artificial Immune Approach for Vehicle Detection from High Resolu-

tion Space Imagery, IJCSNS International Journal of Computer Science and Network Secu-

rity (2007) VOL.7 No.2.

2. Juozapavicius, A., Blake R., Kazimianec, M.: Image Processing in Road Traffic Analysis,

Nonlinear Analysis: Modelling and Control, Nonlinear Analysis: Modelling and Control

(2005) Vol. 10, No. 4, 315–332.

3. Higashikubo M., Hinenoya T., Takeuchi K.: Queue Length Measurement Using an Image

Processing Sensor, In 3rd AnnualWorld Congress on ITS, Orland (2005).

4. Ho L. W., Kleeman L.: Real Time Object Tracking using Reflectional Symmetry and

Motion, IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS)

(2006).

5. Gonzalez R.C., Woods, R. E.: Digital Image Processing (2nd ed.), New Jersey: Prentice

Hall (2002).

6. Gonzalez Rafael C. & Woods Richard E. & Eddins

Steven L.: Digital Image Processing

Using MATLAB (Hardcover), Prentice Hall, 1st edition.

if n_cars > 10 then

"Traffic Is Heavy"

n_cars=5

normal

141

7. Stefan, H.: Automatic Road Extraction in Urban Scenes-and- Beyond, Remote Sensing

Technology, TU Munchen (2005).

8. Geoffrey, A., Hollinger: Design and Construction of an Indoor Robotic Blimp for Urban

Search and Rescue Tasks (2005).

9. Zhu Z. & Lu H., Hu J., Uchimura K.: Car Detection Based on Multi-Cues Integration,

IEEE 17th International Conference on Pattern Recognition (ICPR'04) (2004).

10. Peter Toft: The Radon Transform - Theory and Implementation, Ph.D. thesis. Department

of Mathematical Modeling, Technical University of Denmark (1996).

11. Darbari M. , Sanjay M. and Abhay K. S.: Development of Effective Urban Road Traffic

Management Using Workflow Techniques for Upcaming Metrocities like Lucknow (India),

International Journal of Security and ITS Applications (2008) Vol. 2, No. 2, April.

12. Yong K. K.: Accident Detection System using Image Processing and MDR, IJCSNS Inter-

national Journal of Computer Science and Network Security (2007) VOL.7 No.3.

13. Gerhardinger A., D. Ehrlich , M. Pesaresi: Vehicle Detection from Very High Resolution

Satellite Imagery, IAPRS (2005) Vol. XXXVI, Part 3/W24 --- Vienna, Austria, August 29-

30.

14. Hinz, Stefan: Detection and Counting of Cars in Aerial Images, Processding of The Inter-

national Conference of Image Processing (2003) vol.3. Barcelona.

142