RESAMPLING BASED ON STATISTICAL PROPERTIES OF DATA

SETS

Julia Bondarenko

Department of Economic and Social Sciences, Helmut-Schmidt University Hamburg

(University of the Federal Armed Forces Hamburg), Holstenhofweg 85, 22043 Hamburg, Germany

Keywords:

Resampling, Classiﬁcation algorithm C4.5, Uniform/(truncated) Normal distribution, Kurtosis, Chi-squared

test, Kolmogorov-Smirnov test, Trafﬁc injuries number.

Abstract:

In imbalanced data sets, classes separated into majority (negative) and minority (positive) classes, are not ap-

proximately equally represented. That leads to impeding of accurate classiﬁcation results. Well balanced data

sets assume uniform distribution. The approach we present in the paper, is based on directed oversampling of

minority class objects with simultaneous undersampling of majority class objects, to balance non-uniform data

sets, and relies upon the certain statistical criteria. The resampling procedure is carried out for the daily trafﬁc

injuries data sets. The results obtained show the improving of rare cases (positive class objects) identiﬁcation

with accordance to several performance measures.

1 INTRODUCTION

Numerous machine learning classiﬁcation methods

currently give good performance in numerous prac-

tical problems, such as diagnosing medical problems,

speech recognition, expert systems, robotic process-

ing etc. A starting point for the present study was

an investigation of road injuries number within the

framework of the joint project with police depart-

ments of one of German federal states. The presented

work focuses on temporal factors impact on daily traf-

ﬁc injuries number. The initial data sets of trafﬁc

injuries are imbalanced: daily injuries numbers are

not approximately equally represented, that is, sepa-

rated into majority (negative) and minority (positive)

classes. As a result, minority class is poorly per-

formed by classiﬁcation (S. Ertekin and Giles, 2007),

(S. Kotsiantis and Pintelas, 2006). But our aim is to

detect efﬁciently the important rare cases in number

of injured persons. In fact, the ability to predict pe-

riods of high incidence of road accidents, is really

essential. Rebalancing the class distributions for the

further classiﬁcation, which includes over- and under-

sampling techniques, can be applied in order to solve

this problem at the data level. We propose here a sim-

ple and general resampling procedure, improving a

classiﬁcation performance of daily road injuries num-

ber.

Oversampling method balances data set by in-

creasing the number of minority class objects (ex-

amples). The simplest oversampling method - ran-

dom oversampling - increases the minority class size

by randomly replicating existing minority class ex-

amples (oversampling with replacement). This tech-

niques is attractive exactly due to its simplicity, but

unfortunately, since random oversampling only repli-

cates existing data, it does not add any actual informa-

tion to the data set. The another approach is to over-

sample the positive minority class by creating new ex-

amples. SMOTE (Synthetic Minority Over-Sampling

Technique, see (N. Chawla and Kegelmeyer, 2002))

is the most popular oversampling method here. In

SMOTE minority classes are oversampled by generat-

ing ”synthetic” examples of minority class and adding

them to the data set. As a result, the class distribution

in the data set changes and probability of correctly

classifying minority class increases. Other oversam-

pling approaches were also proposed ((V. Garcha and

Mollineda, 2008), (H. Han and Mao, 2005)). Under-

sampling approaches try to decrease the number of

major class examples. However this method may in-

volve information loss (that is, discard potentially im-

portant for learning and prediction examples, see (X.-

Y. Liu and Zhou, 2006)).

Naturally, well balanced data sets assume uniform

distribution. The approach we present in the paper,

is based on directed oversampling of minority class

objects with simultaneous undersampling of major-

143

Bondarenko J.

RESAMPLING BASED ON STATISTICAL PROPERTIES OF DATA SETS.

DOI: 10.5220/0002171701430148

In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2009), page

ISBN: 978-989-8111-99-9

ity class objects, to balance non-uniform data sets (to

ensure the uniform distribution), and relies upon the

statistical criteria. The remaining parts of the paper

are organized as follows. In Section 2, we discuss

the initial injuries data sets used in our work and per-

form their classiﬁcation according to several metrics.

Resampling procedure description and new classiﬁ-

cation results are presented in Section 3. Section 4

contains conclusions, brief discussion of ongoing and

potential future research topics.

2 CLASSIFICATION OF INITIAL

DATA SETS

2.1 Data Sets and Attributes

Data sets used in our study include the daily num-

ber of injured persons in trafﬁc accidents in two cities

of North Rhine-Westphalia, Germany - Duesseldorf

and Duisburg, for the period 2004-2006. The daily

data for each city represent an age group 25-59 years

old people. Table 1 shows the mean, mode, median,

minimum and maximum values for each region, as

well as skewness and kurtosis, which are the mea-

sures of the data sets asymmetry and peakedness, re-

spectively. Note, that we removed before all ”heavy”

outliers from the data sets, as sensitive to outliers.

”Heavy” outliers are identiﬁed as all values more than

3IQR above the 3rd or below the 1st quartile, where

IQR = Q

−Q

is interquartile range, Q

and Q

are

3rd and 1st quartiles correspondingly.

Table 1: Descriptive Statistics of Data Sets.

value Duesseldorf Duisbirg

mean 5.03 2.43

min 0 0

max 19 12

mode 4 1

skewness 0.65 0.92

kurtosis 3.67 4.02

Histograms showing distribution of injured per-

sons for each urban region for period 2004-2006, are

presented in Figure 1.

Let Y

i,t

be the number of injured at the day t, t =

1, ..., 1096 (3 years, 2004-2006) in region i, i ∈ I =

{

1, 2

}

(1=Duesseldof, 2=Duisburg). We treat as at-

tributes the certain day features related to correspond-

ing outcomes Y

i,t

, namely:

• year: 1=2004, 2=2005, 3=2006;

• month: 1=January, 2=February,..., 12=December;

Figure 1: Histograms of Daily Number of Trafﬁc Injured

Persons for Age Range 25-59, 01.01.2004-31.12.2006.

• school vocation day: 1=yes or 0=no;

• holiday (ofﬁcial): 1=yes or 0=no;

• weekday: 1=Monday, 2=Tuesday,..., 7=Sunday;

• bridge day: 1=yes or 0=no.

The distribution for Region 1 looks roughly sym-

metric and just lightly (positively) skewed, data set

for Region 2 shows more skewed behavior. Each data

set has relatively narrow range of values - 0 ÷19 for

Region 1 and 0 ÷12 for Region 2.

A number of algorithms has been developed for

decision tree construction, but we will dwell upon one

of them - C4.5-algorithm (Quinlan, 1993), based on

the computing the metrics known as the information

gain (IG) and gain ratio (GR). We introduce a notion

of IG as follows:

IG(S

, A) = E (S

) −

∑

i∈values(A)

E (S

) , (1)

where E (S

) = −

∑

log





is entropy of the en-

tire data set S

= (Y

, ...,Y

) of size n, n

is the number

of instances in S

with value k, E (S

) is entropy of

the sample S

of size l

involving elements from Y,

which correspond to the outcome (value) A

of the at-

tribute (feature) A, and

represents the fraction of the

data in S

that goes into S

In C4.5 algorithm below we adopt the information

gain ratio to select the best day attribute to branch on

at each stage. Attribute with the highest gain ratio

gives us the crucial information concerning the tem-

poral distribution of trafﬁc injuries number inside the

each region.

The formula aggregates over the different values

attribute A can have. But IG would be biased to-

wards selecting attributes with more values. To miti-

gate this effect, we use a normalized version of IG -

Gain Ratio (GR), deﬁned as follows:

GR(S

, A) =

IG(S

, A)

Split In f o (S

, A)

, (2)

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

144

where split information Split In f o (S

, A) =

∑

i∈values(A)





is the entropy of partitioning, or

in other words, entropy associated with the distri-

bution of the attribute A, where

is the probability

(proportion) of observing the ith value of A. Thus, a

large number of small partitions is penalized there.

2.2 Evaluation Measures

In the ﬁrst place, we employ the Accuracy traditional

metric, that is the percentage of the correctly classi-

ﬁed data. An information about actual and predicted

examples is contained in confusion matrix (Kohavi

and Provost, 1998). The entries in the confusion ma-

trix have the following meaning in our problem:

T N is the number of correct predictions that an exam-

ple is from negative class;

T P is the number of correct predictions that an exam-

ple is from positive class;

FN is the number of incorrect predictions that an ex-

ample is from negative class;

FP is the number of incorrect predictions that an ex-

ample is from positive class.

The Accuracy is computed then as a proportion:

Accuracy =

T P+T N

T P+T N+FP+FN

But for classiﬁcation of imbalanced data sets,

accuracy is no longer a proper measure since mi-

nority class has very small impact on the accuracy.

Therefore, the following alternative evaluation mea-

sures (metrics) were proposed and used, for instance,

in (G. Cohen and Geissbuhler, 2005), (Hido and

Kashima, 2008), (Kubat and Matwin, 1997):

- True Positive Rate (TPR), or Recall. The pro-

portion between correctly classiﬁed positive examples

and that are calculated: Recall= T PR =

T P

T P+FN

- Precision. The proportion between correctly

classiﬁed positive examples and that are actually cor-

rect: Precision=

T P

T P+FP

- G-mean (Geometric mean). Tries to maxi-

mize the accuracy on each of the two classes while

keeping these accuracies balanced: G − mean =

√

Positive Accuracy ∗Negative Accuracy,

where Positive Accuracy =

T P

T P+FN

=Recall,

Negative Accuracy =

T N

T N+FP

- F-measure. ”The trade-off” between precision

and recall, drops rapidly if either precision or recall is

poor: FM =

2Recall∗Precision

Recall+Precision

2.3 Classiﬁcation Results

In Section 2.1 we have noted that each data set

S is kept within a certain limited relatively nar-

row range of values. That allows us to consider

every value of the range ν

, where v = (v

)

(min(S), ..., max(S))

, as a separate class:

Class 1: ”0 Injured Persons per Day”, Class 2: ”1

Injured Person per Day”,..., Class r ”r Injured Persons

per Day”, where r = 19 + 1 = 20 for Region 1 and

r = 12 + 1 = 13 for Region 2. Thus, we transform

here count data into categorical ones. Of course, we

could group the data or consider continuous data as

well.

We make no assumption about the distribution of

the daily number of persons injured in trafﬁc acci-

dents, except its unimodality during the resampling

procedure. The unimodality of initial data sets is also

established in the frequency distribution histograms,

see Fig. 1. Remind, that a distribution is called uni-

modal if there is only one major ”peak” (mode) in the

distribution. Let M be mode of the data set, and ϕ

its frequency. We select all values of daily number of

injured persons ν, those frequencies are lying within

the interval from 0.8 ϕ

till ϕ

, to be ”negative”, or

majority, class S

neg

. All the other values combined

together represent ”positive”, or minority, class S

pos

The classiﬁcation procedure with algorithm C4.5

gives the following results for both regions, which

we present below. The classiﬁcation is performed by

means function J48() implemented in RWeka pack-

age, R statistical software. The minimal number of

instances per leaf we set to 20. The evaluation mea-

sures deﬁned in previous subsection, are computed ei-

ther.

The classiﬁcation results for both regions are reported

below. Only about 18% of examples are classiﬁed

correctly for Region 1, with low magnitudes of alter-

native measures.

CLASSIFICATION RESULTS FOR REGION 1:

Correctly Classified Instances 18.3394 %,

Recall = 0.1325, Precision = 0.0676,

G-mean = 0.1650, F-measure = 0.0895.

Majority (negative) class is presented here by

numbers 3, 4 and 5. All the others are classiﬁed into

the minority class. For the Region 2 we have at the

beginning about 26% of correctly classiﬁed examples

CLASSIFICATION RESULTS FOR REGION 2:

Correctly Classified Instances 26.2774 %

Recall = 0.2449, Precision = 0.1347,

G-mean = 0.2577, F-measure = 0.1738.

Consistently, negative class consists of numbers 1, 2

and 3, the rest of the numbers is in positive class. In

the next Section we describe a resampling strategy,

which improves classiﬁcation performance.

RESAMPLING BASED ON STATISTICAL PROPERTIES OF DATA SETS

145

3 NEW RESAMPLING

PROCEDURE

3.1 Resampling Motivation and

Procedure Illustration

As one can see, in both our data sets, the examples

from minority class are much less ”beloved” by clas-

siﬁcation algorithm than from majority one (common

problem of imbalanced data). Below we present an

algorithm, which resizes/rebalances our data sets.

With accordance to certain criteria, we generate

artiﬁcial data from minority class and simultaneously

withdraw data from majority class, until the classes

are approximately equally represented (data are

uniformly distributed). It may be considered as a

preprocessing procedure for further classiﬁcation and

prediction.

The algorithm assumes unimodal character for

frequency distribution of classes, without reference to

skewness (asymmetry) of the distribution. Majority

classes are concentrated around peak M (Figure 2a),

while minority classes are more tails-sited. Our

suggestion is to generate new synthetic data from

singly left- and right-truncated normal (half-normal)

distributions, with truncation points u

le f t

= min(S)

and u

right

= max (S), respectively, where u

le f t

and

right

are also the means of truncated normal distri-

butions. At the same time, we ﬂatten the peak of

distribution, picking out the data placed around it.

Such combination of the oversampling the minority

class with undersampling the majority class helps to

achieve better classiﬁer performance.

If more detailed, a random variable is said to be from

a left-truncated normal distribution if its density is

f (x) =

√

2πσ

exp

−

(x −m)

2σ

for x ≥u

le f t

, f (x) = 0 for x < u

le f t

, (3)

where m is a mean and σ is a standard deviation of

the distribution, q is a normalizing quantity with value

obtained from the equation

∞

le f t

f (x)dx = 1. A right-

truncated normal distribution is deﬁned analogously.

We discard elements outside the limit points u

le f t

and

right

, and choose m

le f t

= u

le f t

and m

right

= u

right

This guarantees, that the least popular classes lying

at the ends of data range interval, will be treated

most intensive. Choosing the desired level of signif-

icance α , we put the critical points (conﬁdence inter-

vals endpoints with 100 (1 −α)% -conﬁdence level)

1−α

le f t

and C

right

for both truncated distributions equal

to M. Thus, the majority class will be also main-

tained, as artiﬁcially generated data can be also out

of endpoints C

1−α

le f t

and C

right

. The standard devia-

tions of the truncated normal distributions can be ob-

tained as σ

le f t

M−m

le f t

1−α

and σ

right

−M

, where

, C

1−α

are critical values of truncated at 0 stan-

dard normal distribution. For example, for α = 0.05:

1−α

= −C

= 1.959964. This is shown schemati-

cally in Figure 2b.

Figure 2: Scheme of Resampling Procedure: a - Underlying

Unimodal Distribution; b - Underlying Distribution (solid

line) and Two Truncated Normal Distributions (dashed and

dotted lines).

As we have noted above, simultaneously with adding

new ”artiﬁcial” observation to positive class, we

drop randomly observation from negative class.

Therefore, we keep the sample size ﬁxed. That helps

us to avoid increasing computational time and losing

information.

In the procedure, we will use the following criteria:

- Chi-squared test (Pearson goodness-of-ﬁt test ). We

have data set S

that is grouped into discrete classes.

Let ϕ denote a vector of observed frequencies of

classes and let ϕ

denote the corresponding vector of

expected (speciﬁed) frequencies. We then calculate

our test statistic:

T =

∑

i=1



−ϕ



, (4)

where r is a number of classes. Under the null hypoth-

esis, this statistic is chi-squared distributed, with de-

grees of freedom equal to r −1 − j, where j is a num-

ber of parameters that should be estimated (for para-

metric case). That is, we can test here a null hypoth-

esis that the frequencies of observed outcomes (daily

numbers of road injuries) follow a speciﬁed (uniform)

distribution, at some chosen level γ. Unfortunately,

this test can be also unsuitable for samples of consid-

erably large size (> 3000). It cannot be also applied

when the expected frequency of any cell is less than

5 or the total n is less than 50. But in our case this

test is appropriate, so further we apply it as a primary

criterion.

- One-sample Kolmogorov-Smirnov nonparametric

test (KS-test). Let S

{

, ...,Y

}

be as before

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

146

our data set, with distribution function F (y). We wish

to test the null hypothesis H

: F (y) = F

(y) for all y

against the alternative H

: F (y) 6= F

(y), where F

(y)

is a completely speciﬁed distribution function (in our

case - function of uniform distribution). Test on H

is determined by Kolmogorov-Smirnov statistic

= sup

−∞<y<∞

(y) −F

(y)

, (5)

where F

(y) is the empirical distribution function

deﬁned by F

(y) =

∑

i=1

{

< y

}

. That is, the

Kolmogorov-Smirnov test tries to determine if dis-

tribution of our data set differs signiﬁcantly from

the speciﬁed hypothetical distribution (here - the uni-

form hypothetical distribution). The null hypothe-

sis is rejected at level γ if the computed value D

is larger than the critical value C

. The critical val-

ues of Kolmogorov-Smirnov test statistic depend on

the sample size. For large samples (≥ 40) one uses

asymptotic critical values, which are strictly decreas-

ing functions of the sample size: for example, the crit-

ical value at the γ = 0.05 level is approximately

1.36

√

where n is sample size. Obtaining the value D

for considerably large n (> 3000) may dramati-

cally increase computational time. Another problem

is that Kolmogorov-Smirnov test doesn’t work well

with discrete (count) data. This problem could be

solved, for example, by the following way: we can

transform our data to continuous ones by means of

Monte Carlo simulation, and then apply Kolmogorov-

Smirnov test to the empirical distribution function of

continuous simulated data and the speciﬁed distribu-

tion F

(y).

- As we constrain a uniform distribution, one can

use a value of kurtosis for distribution control. Re-

mind, that kurtosis is the degree of peakedness of a

distribution. Removing observations from the center

to the tails and ”shoulders” of the distribution will de-

crease kurtosis, making the initial leptokurtic distri-

butions more platykurtic. A uniform distribution has

a kurtosis of 1.8. Thus, kurtosis could be used. as a

simple parameter for comparison data set distribution

with uniform ones: if

µ(S

) −µ

< ε , (6)

where µ

= 1.8, µ(S

) is kurtosis of S

, and 0 < ε < 1,

we stop resampling procedure.

3.2 Classiﬁcation Results

We can now see that the C4.5 algorithm improves

its classiﬁcation performance when we apply it to re-

balanced data sets. In our example, we have chosen

γ = α = 5%. The percentage of correctly classiﬁed

instances after resampling procedure have increased

from 18% to 35% for Region 1, from 26% to 37% -

for Region 2 (see below). Our approach also yields

promising results in terms of the alternative perfor-

mance measures.

CLASSIFICATION RESULTS FOR REGION 1:

Correctly Classified Instances 35.0365 %,

Recall = 0.3089, Precision = 0.5783,

G-mean = 0.3734, F-measure = 0.4027.

CLASSIFICATION RESULTS FOR REGION 2:

Correctly Classified Instances 37.5 %,

Recall = 0.3477, Precision = 0.6476,

G-mean = 0.3972, F-measure = 0.4525.

The histograms indicate approximately uniform

distributions after procedure completion, with kurto-

sis magnitudes equal to 1.8643 and 1.7894, respec-

tively.

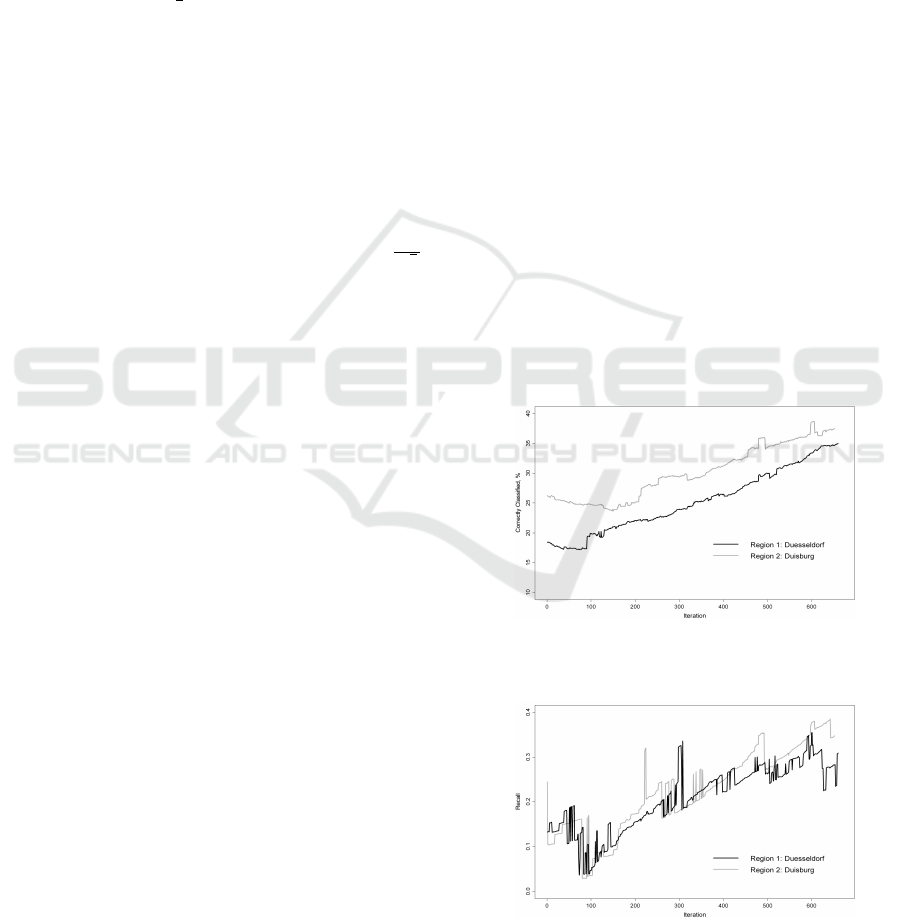
Reporting our experimental results in dynamics,

one can see in Figures 3-5, that the measures those

we are interested in, are increasing (although non-

monotonically) with the iteration number. In each

ﬁgure, we plot every classiﬁcation measure for both

regions: percentage of correctly classiﬁed examples

(Figure 3), Recall (Figure 4), Precision (Figure 5) (G-

mean and F-measure plots are not presented here by

lack of space).

Figure 3: Algorithm Performance for Regions: Accuracy,

Figure 4: Algorithm Performance for Regions: Recall.

Note, that Precision lines are lying almost everywhere

above all other lines. This tells us that proportion of

RESAMPLING BASED ON STATISTICAL PROPERTIES OF DATA SETS

147

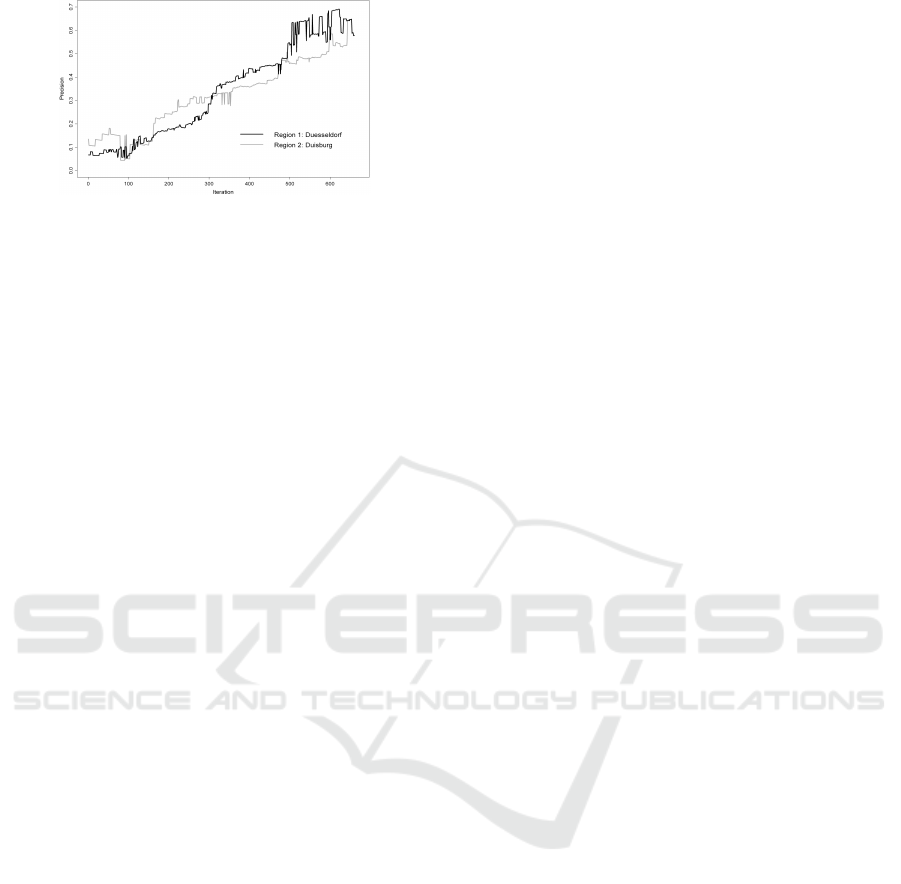
Figure 5: Algorithm Performance for Regions: Precision.

examples that were classiﬁed as elements from posi-

tive classes and those that are actually positive, grows

most rapidly.

4 CONCLUSIONS AND FUTURE

RESEARCH WORK

In this paper, a resampling technique based on statis-

tical properties of data set, was proposed. We have

tested our technique in terms of its accuracy and four

performance measures: Recall, Precision, G-mean

and F-measure. As investigation reveals, C4.5 algo-

rithm applied to resampled data sets produced better

results. But, in spite of the presented promising direc-

tion of rather general resampling techniques, the algo-

rithm has to be yet improved in terms of classiﬁcation

performance. The effect of its application to various

forms of data sets structure (highly skewed data sets,

multimodal data sets, etc.) should be investigated as

well. The comparison with other resampling methods

also has to be carried out.

The resampling algorithm can be also carried out

on the basis of the likelihood ratio test. The Neyman-

Pearson Lemma implies that likelihood ratio test gives

the best result in ﬁxed size samples.

Further, for the start-up problem we were interested

in, an accurate classiﬁcation can result in injuries

control boundaries analogous to presented in (Bon-

darenko, 2006a), (Bondarenko, 2006b), (F. Pokropp

and Sever, 2006). The trees obtained by classiﬁca-

tion, can be very large (a lot of nodes and leaves), and

in this since they are less comprehensible for control

boundaries illustration. But we can simplify the ob-

tained classiﬁcation results by transforming every de-

cision tree into a set of ”if-then” rules (”Trafﬁc In-

juries Rules”), which seem to be easier for under-

standing and interpreting. Using real trafﬁc injuries

data, it is possible to develop realistic model for daily

injuries number prediction, depending on temporal

factors (year, month, day type). Of course, this re-

search direction is open for other practical implica-

tions as well.

REFERENCES

Bondarenko, J. (2006a). Analysis of trafﬁc injuries among

children based on generalized linear model with a la-

tent process in the mean. Discussion Paper in Statis-

tics and Quantitative Economics, Helmut-Schmidt

University Hamburg, (116).

Bondarenko, J. (2006b). Children trafﬁc accidents mod-

els: Analysis and comparison. Discussion Paper

in Statistics and Quantitative Economics, Helmut-

Schmidt University Hamburg, (117).

F. Pokropp, W. Seidel, A. B. M. H. and Sever, K. (2006).

Control charts for the number of children injured in

trafﬁc accidents. In H.-J. Lenz, P.-T. W., editor, Fron-

tiers in Statistical Quality Control, pages 151–171.

Physica, Heidelberg, 5 edition.

G. Cohen, M. Hilario, H. S. S. H. and Geissbuhler, A.

(2005). Learning from imbalanced data in surveil-

lance of nosocomial infection. Artiﬁcial Intelligence

in Medicine, 37:7–18.

H. Han, W. W. and Mao, B. (2005). Borderline-smote:

A new over-sampling method in imbalanced data sets

learning. In Proceedings of the International Confer-

ence on Intelligent Computing, pages 878–887.

Hido, S. and Kashima, H. (2008). Roughly balanced bag-

ging for imbalanced data. In Proceedings of the SIAM

International Conference on Data Mining, pages 143–

152.

Kohavi, R. and Provost, F. (1998). Glossary of terms. edi-

torial for the special issue on applications of machine

learning and the knowledge discovery process. Ma-

chine Learning, 30:271–274.

Kubat, M. and Matwin, S. (1997). Adressing the curse of

imbalanced training sets: Onesided selection. In Pro-

ceedings of the 14th International Conference on Ma-

chine Learning, pages 179–186.

N. Chawla, K. W. Bowyer, L. O. H. and Kegelmeyer, W. P.

(2002). Smote: Synthetic minority oversampling tech-

nique. Journal of Artiﬁcial Intelligence Research,

16:321–357.

Quinlan, J. (1993). C4.5: Programs for Machine Learning.

Morgan Kaufmann, San Mateo, California.

S. Ertekin, J. H. and Giles, C. L. (2007). Active learning

for class imbalance problem. In Proceedings of the

30th Annual International ACM SIGIR Conference on

Research and Development in Information Retrieval,

pages 823–824.

S. Kotsiantis, D. K. and Pintelas, P. (2006). Handling im-

balanced datasets: a review. GESTS International

Transactions on Computer Science and Engineering,

30:25–36.

V. Garcha, J. S. and Mollineda, R. (2008). On the use of sur-

rounding neighbors for synthetic over-sampling of the

minority class. In Proceedings of the 8th WSEAS In-

ternational Conference on Simulation, Modelling and

Optimization, pages 389–394.

X.-Y. Liu, J. W. and Zhou, Z.-H. (2006). Exploratory un-

dersampling for class-imbalance learning. In Proceed-

ings of the International Conference on Data Mining,

pages 965–969.

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

148