QUANTIFIED ONTOLOGIES FOR REAL LIFE APPLICATIONS

Lucia Vacariu

, George Fodor

Department of Computer Science, Technical University of Cluj Napoca, 26 Baritiu str, Cluj Napoca, Romania

ABB AB Process Automation, Vasteras, Sweden

Gheorghe Lazea, Octavian Cret

Department of Automation, Department of Computer Science, Technical University of Cluj Napoca, Cluj Napoca, Romania

Keywords: Merging Ontologies, Symbolic Approaches to Control, Semantic Services, Mobile Robots.

Abstract: Industrial applications are using run-time symbolic approaches only when formal methods can assign useful

meaning to symbols by computationally inexpensive algorithms. However, most reasoning methods are

either computationally prohibitive or may compute indefinitely; thus such methods have limited use in

industrial applications. In many practical situations, the uncertain environment in which an “intelligent”

control system acts consists of the symbolic space of some other “intelligent” control system, both

networked in the same name space. The result of such interaction is to establish relations between

heterogeneous vocabularies and reasoning agents, and between symbols and the physical environment in

which the connected systems act. This paper introduces and motivates the necessity for on-line

quantification of the degree to which symbols in a system have their intended meaning.

1 INTRODUCTION

The theory presented here has relevance for

distributed real-time systems such as those used in

multi-robot applications or in distributed

manufacturing industries. These systems have a

large set of symbols in the form of names for

components, signals, process states or configuration

parameters. Heterogeneity manifests by units being

of different specialization and of different make.

Having the right meaning of each symbol is essential

for a correct operation of the system. The costs for

matching all signals, communication protocols and

sub-products during a tender process for a complex

system turn out to be a significant part of the total

cost of the system. Moreover, after delivery,

ensuring that the final system behaves according to

specifications can be a lengthy and highly qualified

process. The solution to this problem is to establish

an ontology for the given industrial domain. These

tools need to reduce symbol complexity by

automatic information processing, such as via

semantic web and ontological languages.

It is an uncommon situation today that such

configuration tools work across dissimilar firms or

markets, though many core technologies and

standards are available. On a theoretical level, the

operations needed, such as ontology merging,

alignment composition, union and intersection are

still under research (Furst, 2008).

We stress here that formal design verification

cannot replace the ontological compliance presented

in this paper: even a perfectly designed system that

is formally proven to follow a design might

encounter a complex environment that does not

follow the assumptions in the specification.

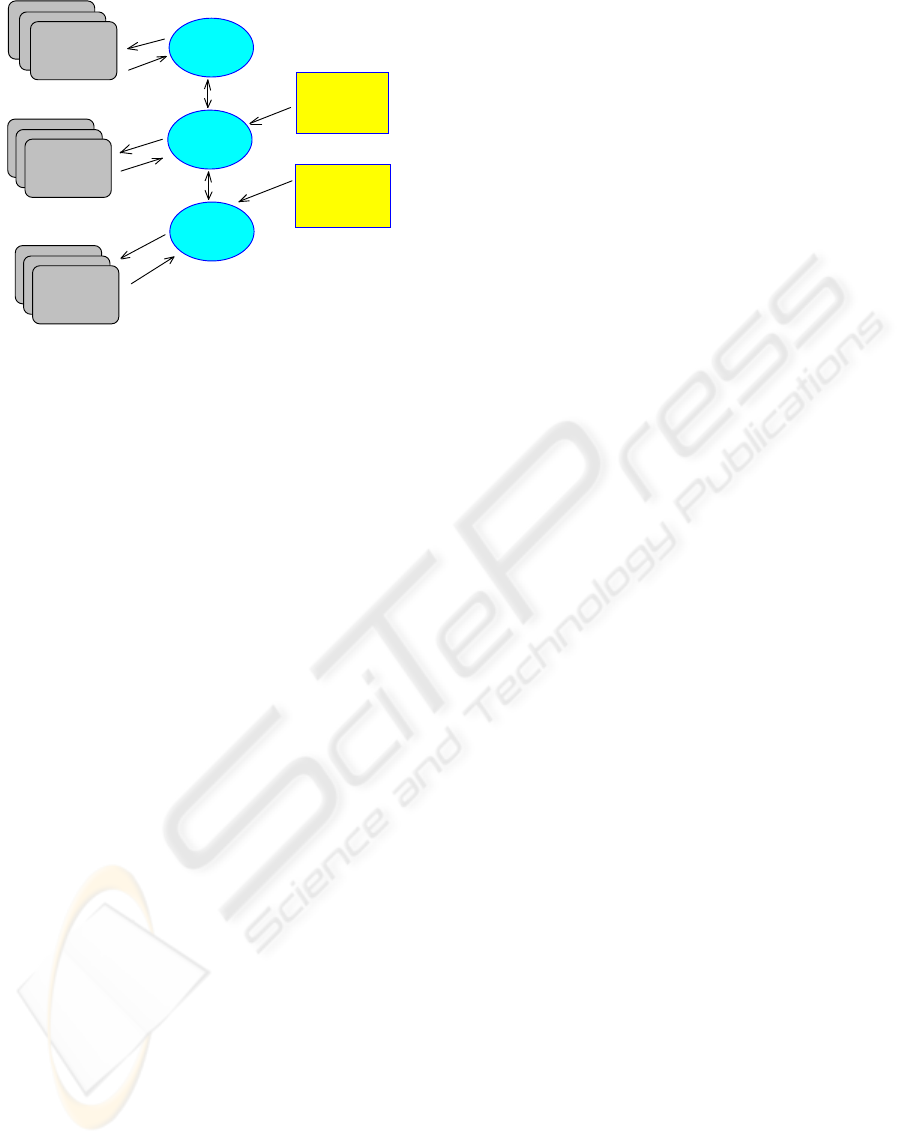
Seen as software architecture, ontologies are

implemented at the current level of technology as

services. These can be organized as local services in

each unit or as a combination of a hierarchic set of

services – local and specialized - with indirections

provided by name servers. Without specifying

details, we call in this paper a generic ontology

service as the “Industrial Ontology Server” (IOS)

(Figure 1).

Practically, an IOS should be able to infer the

structure of any type of distributed industrial

application. Of course, this is a very ambitious

claim, well beyond the forefront of what is available

today in academia or industrial research institutes.

383

Vacariu L., Fodor G., Lazea G. and Cret O. (2009).

QUANTIFIED ONTOLOGIES FOR REAL LIFE APPLICATIONS .

In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 383-386

DOI: 10.5220/0002176103830386

 SciTePress

Manufacturers

Control

Equipment

System

Integrators

and OEM

On-line

Control

System

Compliance

Service

Endorsement

Service

Ontology

Broker

Compliance

Broker

Endorsement

Broker

Bridge

Publish

Fwd Invoke

Figure 1: Federated Service Architecture IOS.

The solution proposed here is to use a minimal,

uniform ontology associated to products and that

each actual systems to update automatically the

required operational and dynamic information into

IOS-es. With this approach, biding costs would be

substantially reduced and market participation would

guarantee more objectivity and flexibility.

Clearly a multi-agent system architecture could

implement such requirements. Tools such as JADE

(Java Agent DEvelopment framework) with Protégé

(Ontology editor and knowledge-base framework)

could handle the design of systems based on a

common design ontology (Tomaiuolo et al., 2005).

2 SOME RELEVANT

TECHNOLOGIES AND

THEORIES

An IOS is relevant if it considers all levels of an

industrial unit included in a system: from signals and

actuators, up to overall goals, including states,

alarms, resource allocation, synchronization with

other units, etc.

2.1 Ontologies in Process Control

Ontologies for automation and process control

applications have several specific layers. At the

design phase, there is available a formal or informal

description of the domain and of the constraints of

the design (Design Model). The standard for

IEC61499 prescribes the Engineering Support

System (ESS) that can perform certain syntactic and

semantic verifications. Valuable research is being

conducted for improving ESS tools (Thamboulidis,

Koumoutsos, and Doukas, 2007).

The framework (middleware) in which the

program, agents or components execute has own

ontology and semantics that limits what the

application program can execute (Execution Model).

Application Ontology. This is the ontology that

effectively decides on goals and actuation. The

domain of discourse is not necessarily the same as

the domain used for the design ontology.

Visualized Ontology. The ontology is typically

visualized on a human-readable interface. The

domain of discourse, taxonomy among objects and

object properties are represented graphically.

Automatic generation of visualization using as input

ontologies expressed in XML/RDF would be an

important advance in technology.

Communicated Ontology. From the execution

model and design data, system designers extract an

ontology used for communicating among

cooperating systems. This ontology may not have

the domain of the Design Model, nor of the

Execution Model.

Ontology does not enter in a formal, verified way

in the design of large control products, as tools are

not mature enough. Another conclusion is that a

system has several ontologies that should be aligned.

There are no commercial tools that can align

ontologies. Interesting research results are reported

using category theory (Zimmermann et al., 2006).

3 METRICS FOR ON-LINE

ONTOLOGIES

3.1 The Decision-Control Space

Essential for taxonomy of process control systems is

the type of actuators used. Actuators are performing

changes in the real world; their semantics is

determined by physical laws.

Independently of the software architecture type,

a control system has two essential parts: (a) a

decision (information) level and (b) a physical,

energy-related level of actuator and plant changes.

All the relevant information from sensed signals

used for decision forms a hyperspace with each

coordinate being one kind of decision information.

Let this space be H with N dimensions,

∈

Chains of decisions generate chains of action

trajectories

1,...,

) in this space.

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

384

Trajectories may not be continuous as disturbances

create ‘jumps’ from one possible trajectory to

another. A valid place on this trajectory is often not

a point but a hyper-sphere (a topology) since usually

control decisions are taken within intervals and not

on discrete points.

In traditional control, the space of all relevant

signals is called a state space and the trajectory a

goal path. Each point reached during control in the

state space is a state. For each state space, a

controller (or agent or component) has mapped a

decision procedure that result in some action being

taken. We are not concerned here with what kind of

decisions or reasoning a controller is doing, but only

with the mapping between actions u

i,j

and spheres

i,j

. Here the variable u denotes an action, and the

variable h denotes a sphere in H. We call the pair S

i,j

= (h

i,j

, u

i,j

) as a state and use first index to denote the

sphere i and the second index to denote a goal path j.

3.2 State Semantics

The active state is the one currently materialized by

sensors. Even if the system consists of many agents

or components, there is always a unique active state

since the hyperspace covers the whole possible

space. However, there may be multiple actions

corresponding to each active state. We represent

here all actions for one point in the hyperspace as a

single action. Some typical state transitions we are

interested in are the following: case (1) - normal

control with no disturbances, case (2) - control with

disturbances and case (3) - lockout.

Performing no action may be a legal, correct

operation of the controller, however if inaction is

due to decision lockout, then this case is distinct and

should be detected.

We seek here moreover to quantify the level of

true semantics states have.

3.3 Quantifying State Semantics

3.3.1 Intra-state Distance

The degree for how “strong” is a state with a current

place h

i,j

in the space H is the inverse of the distance

from h

i,j

to the centre of the sphere intended for that

state. Therefore, closer h

i,j

is to the state sphere

boundary, less correlation it has with the current

state and its action. This is the typical situation when

the true state is somewhere in between two states,

none fully reached; fuzzy logic can quantify and

correct this situation (Grantner and Fodor, 2002).

For a measured probability distribution Q, the

Kullback Leibler divergence of Q from P is:

(P ||Q) = P(i)log

(i)

Q(i)

∑

(1)

3.3.2 Inter-state Endorsement

The following levels of endorsement for a state are

defined to characterize how well predictions are

built into the semantics of a state materialize.

Void-Endorsement. A state is void-endorsed if it is

materialized. That means for a state S

i,j

= (h

i,j

, u

i,j

)

ve(S

i,j

) iff (h

i,j

∧ u

i,j

)

(2)

This is the simplest form of endorsement, but it

tells an important think: that the program semantics

about the environment matches at least once a real

instance of the environment. The properties matched

are those in h

i,j

Weak State Endorsement. A state is weakly

endorsed if a consecutive state of a void-endorsed

state placed on the same goal path is weakly

endorsed at the next instance of time.

we(S

i,k

) iff ve(S

i,k

) ∧ O ve(S

j,k

)

(3)

Here ‘O’ is the ‘next time’ logical operator; both

states are on the same path T

as the second index k

shows. A we() state is not a goal state. Weak

endorsement means that if a state has materialized

and the controller has executed an action at that

state, then the expected outcome really turned out to

be true in the environment.

Strong State Endorsement. A state is strongly

endorsed if a consecutive state on the same path

materializes and both states are weakly endorsed.

se(S

i,k

) iff we(S

i,k

) ∧ O we(S

j,k

)

(4)

A se() state is again not a goal state. This state

endorsement tells that after a state materialize and

the action executed, a next expected state indeed

materializes as well and moreover the action from

that second state has the expected effects.

3.3.3 Goal Path Endorsement

Goal paths are endorsed in similar way as states.

Void Endorsed Goal Path. A goal path T

is void

endorsed if there exists a state that is not the goal

state of the path and which is weakly endorsed:

QUANTIFIED ONTOLOGIES FOR REAL LIFE APPLICATIONS

385

vpe(T

) iff

∃

i ve(S

i,k

)

(5)

A void-endorsed goal path has some h

i,j

of some

state that materializes in the environment, moreover

the corresponding action is being executed, but there

is no evidence that any of the following expected

states on the same goal path have been materialized.

Note that there may be states that are not on any goal

path, so a void endorsed state may not necessarily

mean a void endorsed goal path.

Weakly Endorsed Goal Path. A goal path T

weakly endorsed if there exists some state on the

goal path that is weakly endorsed and which is not

the goal state of the path.

wpe(T

) iff ∃i we(S

i,k

)

(6)

A weakly endorsed goal path has at least one

state that when acting on the path, get expected

effects on the same goal path. However, it is not sure

that the expected state has the required quality that

even its action will get expected results and thus the

semantics of the second reached states is not entirely

sure.

Strongly Endorsed Goal Path. A goal path T

strongly endorsed if there exists a state that is

strongly endorsed on the goal path.

spe(T

) iff ∃i se(S

i,k

)

(7)

More generally, a goal path is n-strongly

endorsed if there are n states which are strongly

endorsed on the path. N-strong endorsement tells

that many states on the goal path are semantically

right, but there may be disturbances that materialize

states interleaved with disturbances, on some other

goal paths. The condition that one full goal path is

traversed without interruption is given by the full-

goal path endorsement: a goal path is full-goal

endorsed if all the states of the goal path materialize

in expected order up to the goal state. Clearly all

states of a path that has full-goal endorsement are

strongly endorsed, except the goal state and the state

immediately before the goal state that is weakly

endorsed.

3.3.4 Global Semantic Norms

Many types of norms can be conceived to quantify

the level of true semantics using the endorsements

given above. For example if |h

i,j

| is a normalized

distance from the center of a state hyper-sphere to

i,j

so that |h

i,j

| ≤ 1 and the norm |se(S

i,k

)| gives the

number of states on the current goal path from the

state i to the goal state, then a measure of the

semantics of the current goal path, SM, is:

SM(T

)=|h

i,j

| +|se(S

i,k

(8)

SM is a continuous, real valued function that

shows how much of the current goal path has been

completed.

4 CONCLUSIONS

Complex systems such as mobile robots systems, or

distributed industrial control systems need to

communicate and use ontological information about

their environments and about the tasks they perform.

Symbolic operations using formal methods are as yet

prohibitive due to computational reasons while

manual work raises substantially the costs of such

systems. This paper presents a method that combines

ontological operations defined formally with

automatic updates for control ontology based on on-

line direct sensory and actuation data.

REFERENCES

Furst, F., 2008. Ontology Matching with Axioms and

Conceptual Graphs. In IEEE Intelligent Systems. Vol.

23, No. 6, pp. 73-75.

Grantner, J.L., and Fodor, G.A., 2002. Fuzzy Automaton

for Intelligent Hybrid Control Systems. In

Proceedings of the 5-th Hybrid Systems Symposium.

2002, Stanford, USA.

Thamboulidis, K.C., Koumoutsos, G.V., and Doukas,

G.S., 2007. Semantic Web Services in the

Development of Distributed Control and Automation

Systems. In Proceedings of the IEEE International

Conference on Robotics and Automation. April 10-14,

2007, Roma, Italy.

Tomaiuolo, M., Turci, P., Bergenti, F., Poggi, A., 2005. A

Two-Level Approach for Ontology Management in

Multi-Agent Systems. In WETICE 2005, Proceedings

of the 14th IEEE International Workshops on

Enabling Technologies: Infrastructure for

Collaborative Enterprise. June 13-15, 2005, pp. 21-26.

Zimmermann, A., Krötzsch, M., Euzenat, J., and Hitzler,

P., 2006. Formalizing ontology alignment and its

operations with category theory. In FOIS 2006,

Proceedings of the International Conference on

Formal Ontology in Information Systems. November

9-11, 2006, Baltimore, Maryland, USA.

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

386