TWO-STAGE ALGORITHM FOR PATH PLANNING PROBLEM

WITH OBSTACLE AVOIDANCE

Mustafa Dogan and Nizami Gasilov

Baskent University, Faculty of Engineering, Eskisehir Yolu 20. km, Baglica, 06810 Ankara, Turkey

Keywords: Path planning, Obstacle avoidance, Graph theory, Dijkstra’s algorithm.

Abstract: The path-planning problem is considered for mobile robot inside environment with motionless circular

obstacles in different sizes. The robot is expected to reach a given target by following the shortest path and

avoiding the obstacles. The two-stage algorithm is proposed to solve the problem numerically. In the first

stage a line-arc based path is found by using geometric techniques. This path cannot be minimal. However,

its length can be used to restrict search space to an ellipse, which contains the minimal path. Thus, the

reduced search space makes the next stage more efficient and endurable for real-time applications. In the

second stage of the algorithm, by discretization of the restricted elliptic region the problem results in finding

the shortest path in a graph and is solved by using the Dijkstra’s algorithm. The proposed two-stage

algorithm is verified with numerical simulations. The results show that the proposed algorithm is successful

for obtaining an optimal solution. The applicability of the proposed algorithm is validated by practical

experiment.

1 INTRODUCTION

Various methods have been proposed for the

solution of obstacle avoidance problem. One of the

real-time methods that has been developed for

navigation of mobile robots is potential field

approach (Connoly et al., 1991; Rimon and

Koditschek, 1992). The main advantage of this

method is on-line efficiency as a result of the

integration of the low-level robot control and path

planning. However, its main disadvantage is that in

some cases it could not escape from local minima

that result in abnormal termination without reaching

the target. Harmonic potential functions (Connoly et

al., 1991) and navigation functions (Rimon and

Koditschek, 1992) are proposed to overcome these

difficulties and in this way obstacle avoidance is

succeeded, but optimal path finding cannot be

achieved. Besides, navigation functions are difficult

to calculate and impossible to be implemented in

real-time, especially for robots that have many

degrees of freedom (Kavraki et al., 1996).

Furthermore, navigation functions should be

differentiable by the definition and therefore, they

can cause problems in piece-wise continuous or

saturated robot control applications (Rimon and

Koditschek, 1992). Nevertheless, potential field

method is improved by the recent advances in both

theoretical and application aspects, e.g. 3-D

extension (Chuang, 1998; Chuang and Ahuja, 1998;

Ren et al., 2006; Cowan, 2007).

Probabilistic roadmap for path planning is just

another alternative method (Kavraki et al., 1996,

1998). This method, in comparison with the previous

ones, can be more reliable and applicable in more

general cases. On the other hand, theoretic analysis

becomes more complex, which is an important

disadvantage of this method.

Some other efficient shortest-path algorithms for

mobile robots are also proposed based on graph

theory approach (Helgason et al., 2001; Liu and

Arimoto, 1992). Finally, dynamic programming

(Hamilton-Jacobi-Bellman) methods are used

extensively as well (Dreyfus, 1965; Moskalenko,

1967, Sundar and Shiller, 1997). For example, in

(Sundar and Shiller, 1997), near-optimal solutions

for the shortest path problem have been obtained by

applying the geometric approach efficiently. The

disadvantage of this method is that it lacks the

minimal path in some cases.

In this research, inspired by the last three

approaches (Helgason et al., 2001; Liu and Arimoto,

1992; Sundar and Shiller, 1997) a new two-stage

optimization algorithm is developed. At the first

stage, near-optimal solution is provided by

165

Dogan M. and Gasilov N. (2009).

TWO-STAGE ALGORITHM FOR PATH PLANNING PROBLEM WITH OBSTACLE AVOIDANCE.

In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 165-170

DOI: 10.5220/0002185001650170

 SciTePress

geometric incremental approach, and this solution is

used to describe the elliptic region that contains the

shortest path. Thus, the optimal solution can be

readily searched after the completion of the first

stage by Dijkstra’s algorithm.

Different from the graph-based heuristic

algorithms, e.g. A* (Dechter and Pearl, 1985; Hart et

al., 1968; Hart et al., 1972; Nilsson, 1980; Bruce

and Veloso, 2006), the proposed method does

guarantee that the selected path is optimal.

Furthermore, A* algorithm can result in the much

longer path than Dijkstra’s one, depending upon

crucial choice of the heuristic function and world

configuration.

The most important novelty of this work is that

the initial search space is reduced a lot in order to

find the shortest path efficiently. Therefore, two

main disadvantages of Dijkstra’s algorithm, namely

large computational burden and difficulty with

following the discrete paths (Helgason et al., 2001),

have been overcome by search space reduction and

greedy path construction approach that explained in

Section 4. These two properties are indispensable in

real-time applications.

2 PROBLEM DEFINITION

Suppose, motionless circular obstacles located in

rectangular domain (search space) are given in finite

number. It is assumed that no obstacle cuts or

touches any other obstacle. The motivating question

behind this research is how point robot can navigate

on the shortest path from a given starting point S to a

given target position F with obstacle avoidance.

Note that, the condition about point robot is not a

restriction for the problem. Let the robot be circular

with radius

. If we enlarge all obstacles in the

amount of

radius-wise, then the robot itself can

be considered as point robot.

Also note that, the proposed approach can be

easily extended for the case when other types of

obstacles such as ellipses, convex polygons are

considered together with circles.

Two-stage algorithm is proposed for numeric

solution to the problem. The detailed explanations of

these stages are given in the following sections.

3 INCREMENTAL METHOD

BASED ON GEOMETRY

The method applied at the first stage is incremental

since it is optimal just for one step. The method is

realized by using geometric representations. The

first obstacle on the straight line between the current

position of the object and the target is assumed to be

a single obstacle in each step of the method. In

accordance with this, the tangential path is

determined firstly from the initial point to this

obstacle. Besides, extra obstacles are controlled

whether they intersect the path or not. If not (refer to

Section 3.1), this path is used to reach the obstacle.

Then, the path is followed along the boundary of the

obstacle until the point, where tangent from the

target touches the obstacle. This point becomes the

new starting point for the next step. If there are extra

obstacles across the tangential path that connects the

initial point S and the first obstacle (refer to Section

3.2), then the extra obstacle that is closest to S will

be determined. This extra obstacle is reached along

the tangential path closer to the baseline SF and

avoided by following its boundary. Then, arrival

point is determined as new starting point for next

step. This process will be iterated until no obstacle

on the way to target.

3.1 Single Obstacle Avoidance

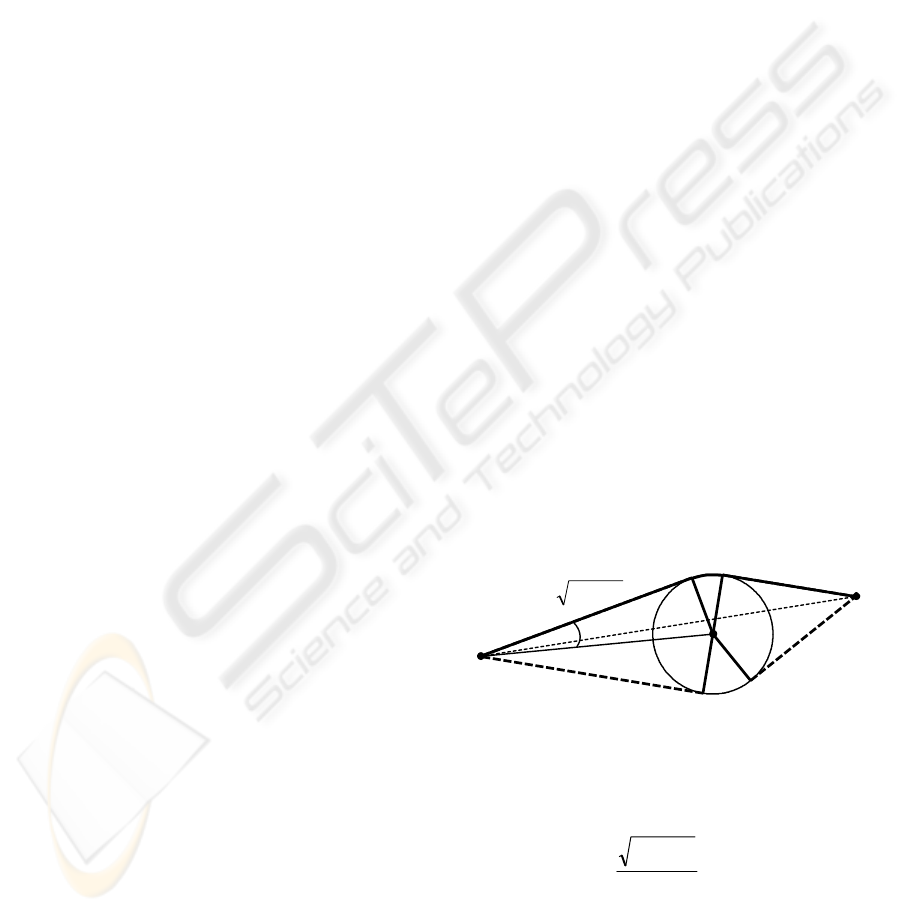
Assume that on the path SF, there is only one

circular obstacle with the radius r and centered at C

as represented in Figure 1. Two pairs of tangent

lines from points S and F can be drawn to the circle.

We can choose the ones that have minimum angle

with line SF, i.e. SA

and FB

in the figure.

Therefore, according to geometrical rules the

shortest path consists of line SA

, arc A

and line

Figure 1: Optimal avoidance of a single obstacle.

In order to calculate coordinates of points A

and

, the following equation can be used:

SCSA

−

= P

Where

SA and SC are vectors;

)/arcsin( lr

;

P is the rotation operator about

point S through an angle

. The sign of

corresponds to choosing one of the points A

and A

rl −

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

166

One of them, which is the closest point to baseline

SF, is selected, either A

or A

We can make a significant evaluation for proving

convergence of approximate method based on

geometry. Since circular obstacle centered at

crosses the line

SF, we have: rd < (Fig. 2). Hence

BFSFBFrCF

dCFHFHFSHSF

>⇒=−>

>−=≥+=

According to last inequality, direct distance to

the target decreases by avoiding an obstacle.

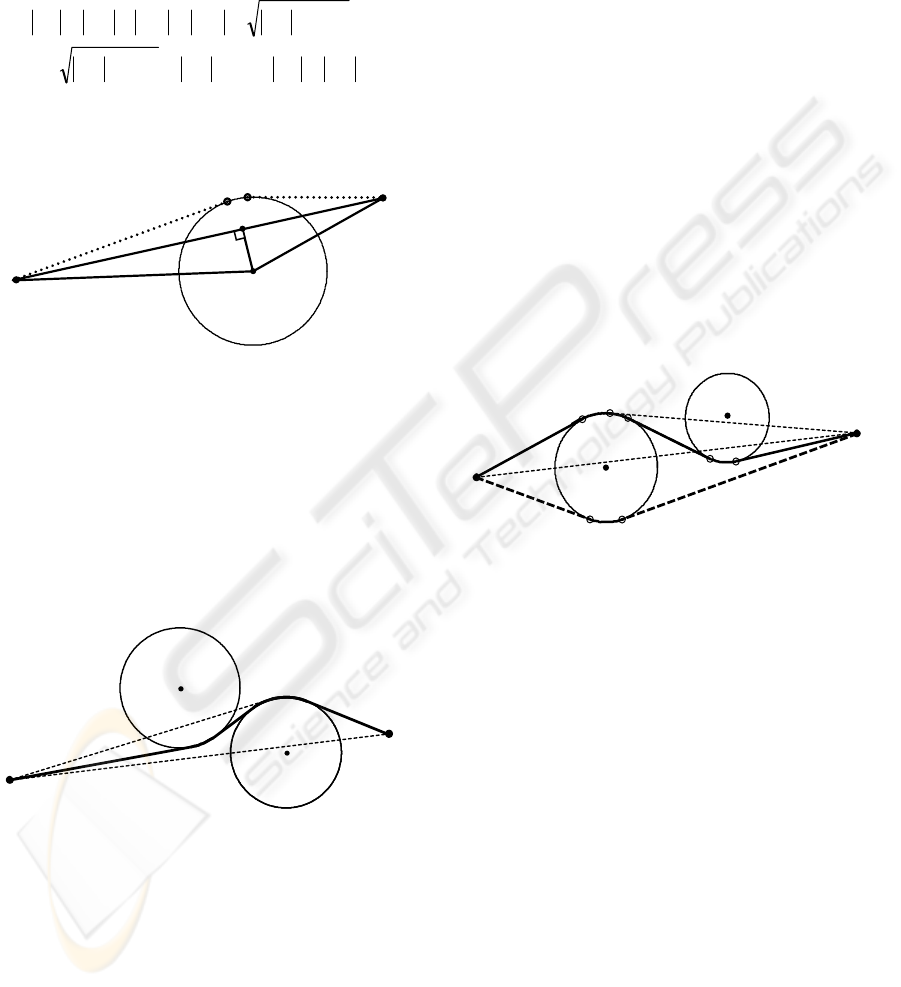
Figure 2: Schematic representation to prove that the direct

distance to the target decreases with obstacle avoidance.

3.2 Extra Obstacle Avoidance

There could be some extra obstacles across the

tangential path SA that is mentioned in Section 3.1.

It is represented in Figure 3 how the path can be

constructed in this case. In Figure 3, the obstacle

centered at

C is ordinary one on the path SF, and the

obstacle centered at E is the extra one.

Figure 3: Avoidance of an extra obstacle.

The algorithm implemented for extra obstacle

avoidance is explained briefly below.

Among extra obstacles crossing tangential path

SA the obstacle that is the closest one to the base

point S is determined, i.e. the obstacle centered at E

in Figure 3. Direction SF will be our reference to

avoid this obstacle. Tangential path

SP close to line

SF is determined. Subsequently, QR, common cross

tangent of obstacles E and C with end point Q close

P, is calculated. The obstacle E has been avoided

by following tangent line

SP first, and then arc PQ.

Then the question is considered whether there is any

other extra obstacle on path

QR, or not. If not, then

by following tangent line QR and arc RB the

ordinary obstacle C will be avoided. If there is an

extra obstacle, new iteration on avoidance of extra

obstacle is started with taking

Q as the new initial

point.

Since number of the obstacles is finite, extra

obstacles will be eliminated after finite number of

steps and an ordinary obstacle will be avoided next.

Refer to end of the Section 3.1, the evaluations

prove that direct distance to the target decreases by

avoiding ordinary obstacle. There is finite number of

obstacles by assumption and the distance to the

target diminishes at each step, then approximate

method based on geometry is convergent.

Geometric method implemented at the first stage

of the main algorithm results in near-optimal

solutions. The path obtained through this method

might not be optimal. Such an example is given in

Figure 4.

Figure 4: An example for which the path obtained by the

geometric method is not optimal.

We can see how the method works for this

example below. Circle C

is the first ordinary

obstacle across the path

SF. According to Section

3.1 this obstacle will be avoided following tangent

path

closer to baseline SF and then arc A

Taking B

as the new starting point, the next step of

the method will be initiated. Circle

is determined

as the ordinary obstacle across path

F. In order to

avoid it, the tangent, which is closer to the baseline

F, is calculated. This tangent line crosses C

Thus, in this time the circle

becomes extra

obstacle when ordinary obstacle

is avoided. The

procedure described in Section 3.2 is implemented

to avoid the obstacle

. Since the starting point B

lies on C

, the step to reach the extra obstacle will be

eliminated. Only arc

Q is used to avoid C

(Here

Q is the end point of QR, common cross tangent of

circles). At the last iteration of the method, by

following tangent line

QR and arc RB, avoidance of

the ordinary obstacle

will be completed and by

TWO-STAGE ALGORITHM FOR PATH PLANNING PROBLEM WITH OBSTACLE AVOIDANCE

167

tangent path

BF the target will be reached. Thus, the

path calculated on proposed geometric method is

QRBF. As it can be easily seen from Figure 4,

this path is longer than the path SA

F, and

consequently, is not optimal.

Thus, in general, solutions obtained through

geometric method are only near-optimal. To find the

optimal path the second stage of algorithm is

applied, which is explained in the next section.

4 OPTIMAL PATH BY

DIJKSTRA’S ALGORITHM

As it is mentioned above, the path obtained at the

first stage might not be the optimal one. However,

its length

gives an upper bound for optimal path

length

L such that

LL ≤ .

The feasible region that contains the optimal path

can be reduced with this inequality on purpose.

Let

X be a point on optimal path. Then it can be

claimed that

****

XFSXSF

LLLL +== .

Since the shortest path should be a line segment

with no consideration for obstacles the following

inequalities can be written:

LSX ≤ and

LXF ≤ . Thus, we get

LXFSX ≤+ .

Regarding this inequality, sum of distances from

S and F to a point X lying in the feasible region

cannot exceed the value

. Subsequently, the

feasible region is inside the ellipse with focuses at

and

F. Hence, based upon the value

L the feasible

region can be diminished and restricted to an ellipse

Thus, the reduced search space makes the second

stage much more efficient and endurable for real-

time applications

In this stage, coordinate transformation is applied

such that new origin will be the midpoint

M of the

line segment SF, and the new horizontal axis will be

in the direction of ray MF. In this new coordinate

system, the feasible region can be described simply

as follows:

()

(

)

1//

≤+ byax

where

La = and 2/)(

SFLb −= . In the

mean time, changing the coordinate system is also

beneficial such that the realizations of the following

steps will be more efficient.

Discretization of the problem is the next step.

For this purpose, a grid with equal squares is created

over the region. The side length of a square, h, is

complied with the minimum distance between

obstacles,

, such that 3/

≤

h . Intersection points

of the grid, or nodes, are assigned as graph vertices.

Thus the analyzed problem can be solved by graph

theory approach. We can define two prohibited cases

such that a) If the vertex N is out of feasible region,

or b) If the square with side length h and centered at

N intersects an obstacle. In both cases, the vertex N

is marked as forbidden to pass. Graph edges can be

constructed in two alternative ways such that:

1) 8-neigborhood vertices around any vertex V,

which is not prohibited, are examined one by one.

The edge is added between the vertex V and the one,

which is permitted to pass.

2) All pairs of vertices (U, V) are to be examined

one by one. If the vertices of a pair (U, V) are not

prohibited and line segment UV does not intersect

any obstacle, the edge with the length |UV| is

constructed between U and V.

At the first alternative, discrete approach is also

used to construct the edges. Therefore, the total

number of edges is minimal and edge structure is

easy to process. In the second alternative, which can

also be characterized as greedy approach, edge

structure is difficult to implement. However, it

provides solution closer to the optimal solution than

the first one does. In simulations, the results of

which are represented in the next section, the second

approach is applied.

Thus, the solution of the problem is reduced only

to find the shortest path from vertex S to vertex F in

the obtained graph. This new problem is solved by

applying Dijkstra’s algorithm (Anderson, 2004).

Furthermore, some improvements have been done

based upon the properties of the problem in order to

make the Dijkstra’s algorithm application more

efficient. For instance, forbidden vertices are not

included to the set of graph vertices. Let

v be the

number of graph vertices. If the first alternative

mentioned above is realized then instead of weight

matrix of size

a zero-one (or binary) matrix of

size

8 is used. Hence, this approach is suitable

for real-time applications. For the second alternative,

as weight matrix is symmetric, then only lower

triangle matrix can be stored at memory.

Note, that in the first alternative the graph is

sparse (number of edges

ve 8~ ). In this case the

complexity of Dijkstra’s algorithm, implemented

with a binary heap, is

)log(~)log( vvOveO .

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

168

5 SIMULATIONS RESULTS

The proposed two-stage algorithm is verified by

many simulations. In simulations the obstacles are

chosen randomly in a rectangular region. The target

position is selected. Then the proposed algorithm is

executed for different starting positions.

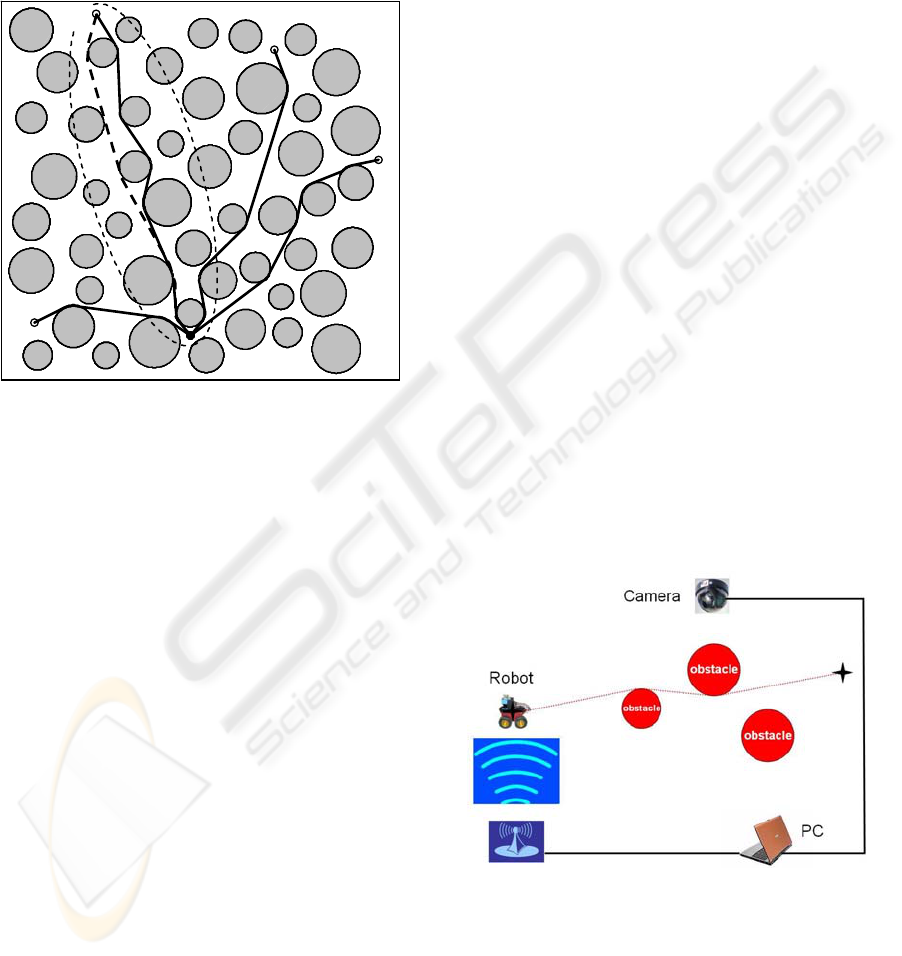
Figure 5: Near-optimal (solid lines) and optimal paths

(dashed line) obtained from calculations in presence of 50

obstacles. Thin dashed line represents the boundary of

elliptic feasible region used at the second stage of the

algorithm.

The results of one simulation are represented in

Figure 5. Here we take scene with size of

120120×=×ba (unit length can be assigned

arbitrarily). We randomly generate circles

),,(

ccc

ryx with radius ]8,4[

∈

r . If next candidate

circle don’t intersects an existing one, we add this

circle to the list of obstacles. Otherwise the

candidate one is rejected.

The paths that are obtained by the first stage

have been represented with solid-line. For one of the

starting points, (S

), optimal path by the second

stage has been shown as dashed-line in Figure 5.

This optimal path has essential differences in

comparison with the result of the first stage (solid-

line starting from S

). For other cases (S

, S

), the

optimal paths, obtained at the second stage, have not

been represented for the purpose of clarity of the

figure, since they do not differ a lot from drawn

ones.

For the case with starting point S

, the boundary

of feasible region, used at the second stage, is shown

by an ellipse (thin dashed-line) in Figure 5. This

ellipse envelops an area, which is about 1/5 of the

whole search space (rectangle). Since the operation

complexity of Dijkstra’s algorithm is

)(

vO and

is proportional to covered area, the benefit of

proposed algorithm is about 25 times better than the

algorithm applied to whole region.

It has been verified by simulations that the

proposed algorithm is useful to solve the

optimization problem for obstacle avoidance.

According to obtained results, in some cases only

the first stage of the algorithm can be sufficiently

used, especially considering robotic applications that

require essential time and memory resources.

Although the proposed algorithm works well for

circular obstacles, more efficient approximations for

obstacles can be obtained by implementing the other

convex figures, e.g. rectangles and ellipses.

Therefore, the geometric method can be extended

easily to cover these shapes. Fortunately, the second

stage of the algorithm is independent from the

shapes of obstacles.

6 EXPERIMENTAL RESULTS

Pioneer 3-DX mobile robot, which has embedded

computer with C++ based ARIA (Advanced

Robotics Interface for Applications) software and

wireless communication capability, has been

controlled by remote PC. Driving capabilities of the

robot are 2-wheel drive, plus rear balancing caster

with differential steering.

Figure 6: Experimental setup.

As shown in Figure 6, after extensive image

processing, necessary path planning commands are

produced by the proposed algorithm that all running

at PC, and are transmitted through wireless network

to the robot. Obstacles are chosen as circular shaped

disks. Besides, their positions are selected in

TWO-STAGE ALGORITHM FOR PATH PLANNING PROBLEM WITH OBSTACLE AVOIDANCE

169

accordance with robot dimensions (swing radius is

32 cm), and minimum inter-distance requirements,

see Section 4.

The first preliminary experiments are done with

two obstacles to evolve the implementation. Finally,

the last experiment is done with five obstacles. After

image processing, the algorithm is implemented in

an efficient way. At the end, the robot followed the

prescribed path successfully as planned beforehand.

For future work, automatic identification and

setting the robot orientation and pose will be an

important achievement, since it took time to set the

right orientation for the robot. Integrating both

stages of the algorithm with image processing to

work in real time while obeying the dynamic

constraints will complete this research project.

7 CONCLUSIONS

Optimization problem for obstacle avoidance on the

plane has been investigated. Two-stage algorithm

has been proposed for solution to the problem and

tested successfully with experiments. In the first

stage, near-optimal solution is obtained through

geometric approach. Using this solution, the feasible

region is restricted to an ellipse. At the second stage

the problem is reformulated as the shortest path

problem in graph, and optimal solution is found by

applying Dijkstra’s algorithm in the reduced search

space. Consequently, two main contributions of this

research come out clearly at the last stage. The first

one, the solution is optimal, and the second one, it is

obtained through an efficient way with a significant

reduction of search space. Simulation results have

proved that the two-stage algorithm complies with

theory and produces accurate solutions.

REFERENCES

Connoly, C. I., Burns, J. B., and Weiss, R., 1991. Path

planning using Laplace’s equation. Proc. IEEE Int.

Conf. Robot. Automat., vol. 1, pp. 2102-2106.

Rimon, E., and Koditschek, D. E., 1992. Exact robot

navigation using artificial potential functions. IEEE

Transactions on Robotics and Automation, vol. 8, pp.

501-518.

Kavraki, L. E., Kolountzakis, M. L., and Latombe, J. C.,

1998. Analysis of probabilistic roadmaps for path

planning. IEEE Transactions on Robotics and

Automation, vol. 14, no. 1, pp. 166-171

Kavraki, L. E., Svestka, P., Latombe, J. C., and Overmars,

M. H., 1996. Probabilistic roadmaps for path planning

in high-dimensional configuration spaces. IEEE

Transactions on Robotics and Automation, vol. 12, no.

4, 566-580.

Helgason, R. V., Kennington, J. L., and Lewis, K. R.,

2001. Cruise missile mission planning: a heuristic

algorithm for automatic path generation, Journal of

Heuristics, Kluwer Academic Publishers, vol. 7, pp.

473-494.

Liu, Y. H., and Arimoto, S., 1992. Path planning using a

tangent graph for mobile robots among polygonal and

curved obstacles. Int. J. Robot. Res., vol. 11, no. 4, pp.

376-382.

Dreyfus, S., 1965. Dynamic Programming and the Calculus

of Variations. New York, London: Academic.

Moskalenko, A. I., 1967. Bellman equations for optimal

processes with constraints on the phase coordinates.

Autom. Remote Cont. (Translation of Avtomatika i

Telemekhanika), vol. 4, pp. 1853-1864.

Sundar, S., and Shiller, Z., 1997. Optimal obstacle

avoidance based on the Hamilton-Jacobi-Bellman

equation. IEEE Transactions on Robotics and

Automation, vol. 13, no. 2, pp. 305-310.

Anderson, J. A., 2004. Discrete Mathematics with

Combinatorics, 2nd Ed. Prentice Hall.

Dechter, R., and Pearl, J., 1985. Generalized best-first

search strategies and the optimality of A*. Journal of

the ACM

, vol. 32, pp. 505 – 536.

Hart, P. E., Nilsson, N. J., and Raphael, B., 1968. A

formal basis for the heuristic determination of

minimum cost paths. IEEE Transactions on Systems

Science and Cybernetics, vol. SSC-4, no. 2, pp. 100–107.

Hart, P. E., Nilsson, N. J., and Raphael, B., 1972.

Correction to a formal basis for the heuristic

determination of minimum cost paths. SIGART

Newsletter, no. 37, pp. 28-29.

Nilsson, N. J., 1980. Principles of artificial intelligence.

Palo Alto: Tioga.

Bruce, J. R., and Veloso, M. M., 2006. Safe multi-robot

navigation within dynamic constraints. Proceedings of

the IEEE, vol. 94, no. 7, pp. 1398-1411.

Chuang, J.-H., 1998. Potential-based modeling of three-

dimensional workspace for obstacle avoidance. IEEE

Transactions on Robotics and Automation, vol. 14, no.

5, pp. 778-785.

Chuang, J.-H., and Ahuja, N., 1998. An analytically

tractable potential field model of free space and its

application in obstacle avoidance. IEEE Transactions

on Systems, Man, and Cybernetics - Part B:

Cybernetics, vol. 28, no. 5, pp. 729-736.

Ren, J., McIsaac, K. A., and Patel, R. V., 2006. Modified

Newton’s method applied to potential field-based

navigation for mobile robots. IEEE Transactions on

Robotics, vol. 22, no. 2, pp. 384-391.

Cowan, N. J., 2007. Navigation functions on cross product

spaces. IEEE Transactions on Automatic Control, vol.

52, no. 7, pp. 1297-1302.

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

170