
Semi-Supervised Least-Squares Support Vector Classifier
based on Virtual Leave One Out Residuals
Stanisław Jankowski
1
, Zbigniew Szymański
2
and Ewa Piątkowska-Janko
3
1
Warsaw University of Technology, Institute of Electronic Systems
ul. Nowowiejska 15/19, 00-665 Warszawa, Poland
2
Warsaw University of Technology, Institute of Computer Science
ul. Nowowiejska 15/19, 00-665 Warszawa, Poland
3
Warsaw University of Technology, Institute of Radioelectronics
ul. Nowowiejska 15/19, 00-665 Warsaw, Poland
Abstract. We present a new semi-supervised learning system based on least-
squares support vector machine classifier. We apply the virtual leave-one-out
residuals as criterion for selection of the most influential data for label switch-
ing test. The analytic form of the solution enables to obtain a high gain of the
computational cost. The quality of the method was tested on the artificial data
set – two moons problem and on the real signal-averaged ECG data set. The
correct classification score is better as compared to other methods.
1 Introduction
The semi-supervised learning consists of numerous methods [1, 2] that attempt to
improve the supervised classifier trained on the labelled data subset L by exploring
the information contained in the (usually larger) subset of unlabelled input data U.
The supervised classifier is considered as an initial hypothesis for classification deci-
sions. In the following steps each unlabelled point is assigned with two alternative
labels, +1 or -1, and the decision is made according to the improvement of the quality
function. Hence, the computation tasks increase quickly for larger number of unla-
belled points [10, 11]. The crucial problem for efficient algorithm is to find simple
solution for the supervised learning and to define a smart criterion for the selection of
the most influential unlabelled points in order to perform the label switching tests.
Our idea of semi-supervised learning system is to use the least-squares support
vector machine (LS-SVM) [3, 4] as supervised classifier and to select unlabelled
points for label switching upon their ranking with respect to the virtual leave-one-out
residuals (VLOO), the influential statistics [5, 6]. The advantage of our idea comes
from the algebraic solution of the LS-SVM and the analytic formula for the VLOO
residuals [7, 8, 9]. We also use the VLOO residuals for pruning the final form of the
classifier. Our method is tested on the artificial data set (two moons problem) and for
Jankowski S., Szyma
´
nski Z. and Piatkowska-Janko E. (2009).
Semi-Supervised Least-Squares Support Vector Classifier based on Virtual Leave One Out Residuals.
In Proceedings of the 9th International Workshop on Pattern Recognition in Information Systems, pages 71-80
DOI: 10.5220/0002196400710080
Copyright
c
SciTePress

the real-life signal averaged ECG data set. We named our system semi-supervised
least-squares support vector machine (SS-LS-SVM).
2 Semi-Supervised Least Squares Support Vector Machine
2.1 General Idea
The idea of semi-supervised least-squares support vector machine is implemented by
the following algorithm:
1. Use LS-SVM classifier for labeled data subset L
2. Initial hypothesis: classify the unlabelled data subset U according to the LS-
SVM rule
3. Calculate the virtual leave-one-out residuals for all points L∪U
4. Rank all points upon the VLOO score
5. Take NUM points of largest VLOO residuals for label switching
6. Go to 2 until the PRESS statistics reaches the required minimal value
2.2 Least-Squares Support Vector Machine
LS-SVM originates by changing the inequality constraints in the SVM formulation to
equality constraints with objective function in the least squares sense [3, 4].
Data set D is defined as:
)},{(
ii
tD x=
}1,1{, +−∈⊂∈
i
d
i
tRXx
(1)
The LS-SVM classifier performs the function:
bf
+
=
)()( xwx
φ
(2)
This function is obtained by solving the following optimization problem:
∑
=
−−+=
l
i
ii
bt
1
22
])([||||
2
1
xww
φγ
L
(3)
In the nonlinear case the kernel function is introduced:
)'()()',( xxxx
φ
φ
⋅
=
K
(4)
Hence, the solution can be expressed as the linear combination of kernels weighted
by the Lagrange multipliers
α
i
:
∑
=
+=
l
i
ii
bKf
1
),()( xxx
α
(5)
The global minimizer is obtained in LS-SVM by solving the set of linear equations
72

⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎦
⎤
⎢
⎣
⎡
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+
−
0
0
!
tα
1
1IK
b
T
γ
(6)
In this work the RBF kernel is applied:
}||'||exp{)',(
2
xxxx −−=
η
K
(7)
Therefore this system is easier to solve as compared to SVM. However the sparse-
ness of the support vectors is lost. In SVM, most of the Lagrangian multipliers α
i
are
equal 0 while in LS-SVM the Lagrangian multipliers α
i
are proportional to the errors
e
i
2.3 Virtual Leave-One-Out Cross-Validation
Leave-one-out cross-validation (LOO) provides the basis for very efficient model
selection. The drawback of such approach is its computational complexity. Each step
of LOO cross validation of an LS-SVM model requires re-computation of linear equ-
ation system (thus inversion of large matrix in case of complex problems) which is
computational expensive. One can perform leave-one-out cross-validation in closed
form without leaving an example out. Let:
)(
ii
fy x
=
(8)
and
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+
=
−
0
1
T
1
1IK
C
γ
(9)
It can be shown that the virtual residual [7, 8]:
1
)()1(
−
−−
=−=
ii
i
i
iii
C
yyr
α
(10)
Hence, the residual r
i
can be computed using information already available as a by-
product of training the LS-SVM classifier on the whole data set.
3 The Algorithm of the Semi-supervised LS-SVM
The input to the SS-LS-SVM algorithm consists of:
• the data set data
L
(which contains labelled data),
• the set L of labels corresponding to the members of the data
L
set,
• the data set data
U
(which contains unlabelled data),
• integer NUM – the parameter describing how many data points are taken in-
to account during label switching,
73

• γ,σ - the hyperparameters of the ls-svm model.
We also make use of two external procedures: trainlssvm (which calculates the α
and b values of the LS-SVM model) and simlssvm (used for classification).
The output of the algorithm consists of the calculated α and b values of the LS-
SVM model, which can be used for classification task.
The algorithm of SS-LS-SVM
Require: data
L
– labelled samples
data
U
– unlabelled samples
L – labels set by the operator,
NUM – parameter of transduction algorithm – number of switched
labels
,- hyperparameters of the lssvm model
trainlssvm – procedure for calculation and b parameters of
the model,
simlssvm – classification procedure, returns the labels
Initialization {
acquire labeled data set L
//creation of the model based on the labeled data
[alpha,b]=trainlssvm(data
L
, L, RBF kernel, , );
//initial labeling of all data samples
L’=simlssvm({data
L
,L,RBF kernel, , },{alpha,b},data
U
);
}
Main loop {
[alpha,b]=trainlssvm(data
L∪U
, L’, RBF kernel, , );
for i=1 to N
L∪U
compute r
i
=alpha
i
/C
-1
ii
//label switching
for NUM largest r
i
{
switch the label in set L’
}
[alpha’,b’]=trainlssvm(data
L+U
, L’, RBF kernel, , );
for i=1 to sizeof(data
L∪U
) compute r
i
=alpha
i
/C
-1
ii
for NUM largest r
i
{
if (r
i
’>r
i
) set previous label
}
}
call pruning procedure
return [alpha, b] //variables describing obtained
classifier
The algorithm is divided into three stages – a) initialization b) computation
stage.and c) pruning stage. During the initialization stage, the ss-ls-svm classifier is
trained using the labeled data set data
L
only (Fig 1.). Thereafter unlabelled data set
data
U
is classified according to the LS-SVM rule. The results of classification are
stored in the label set L’. This is the initial hypothesis – all previously unlabelled data
points are now labeled, however it is possible that not all labels are correct (Fig 2.).
74

Fig. 1. The initialization stage the SS-LS-
SVM classifier – it is trained using the la-
beled data only (black points).
Fig. 2. Initial labelling – marked points
represent potentially misclassified data.
(black points – class +1, grey – class -1)
In the next stage of the algorithm we try to improve the results of initial labelling.
Potentially misclassified data points are selected using the values of virtual residuals
r
i
(computed using the Virtual Leave-One-Out Cross-Validation method [6]). The
labels of the NUM points having largest r
i
value are switched to the opposite value. If
the r
i
value after switching increases then the old label is restored.
Pruning. The last stage of SS-LS-SVM algorithm is pruning of the obtained model
by removing the least relevant data points. The original data set and the decision
boundary calculated for this data set using the LS-SVM model are shown in Fig. 3.
The relevance of the data points is determined by values of virtual residuals r
i
(Fig.
4).
Fig. 3. The decision boundary created using
whole learning data set.
Fig. 4. The values of residuals calculated for
all data points.
The pruned data set contains data points which satisfy the rule
})max({3.0
ii
rr
⋅
≥
(11)
75

This approach significantly reduces the number of support vectors without loss of
the classification score, as shown in Fig. 5.
Fig. 5. The result of pruning and the decision boundary after pruning.
4 Evaluation of the SS-LS-SVM on Artificial Data Set
4.1 The Data Sets
The algorithms were evaluated on an artificially generated two dimensional data set
“Two moons – tm_27749_20”. The data set contains points belonging to two non-
linearly separable classes (positive – labelled as +1 and negative – labelled as -1). The
set was divided into two subsets – the learning set used for creating of LS-SVM mod-
els and the test set for testing of developed algorithms. The training set contains 66
data points: 33 belonging to the positive class and 33 to the negative class (shown in
Fig. 3). The test set contains 134 examples: 67 belonging to the positive class and 67
to the negative class.
The second data set tm_94326 was generated by the same algorithm as
tm_27749_20. It consists of 2000 data points: 666 points assigned to the learning set
and 1334 points of the test set. The data set was used to test the pruning algorithm.
4.2 Evaluation of VLOO Estimator
We studied the properties of VLOO estimator on the “Two moons – tm_27749_20”
dataset described in 4.1. We calculated the leave one out error and its virtual counter-
part (10) for every data point in the learning set. The diagram shown in Fig. 6 con-
tains the plot of VLOO error versus LOO error. The correlation coefficient is equal
0.95. Therefore we can conclude that VLOO calculated by (10) is sufficiently good
estimator of LOO error.
76

Fig. 6. VLOO versus LOO error.
4.3 Criterion for Finding of Potentially Misclassified Examples
We can use (10) to detect potentially misclassified examples. Figure 7a presents arti-
ficially generated two-dimensional data set. One point (0.4890, 0.4002) is intentional-
ly mislabelled. We trained the LS-SVM classifier for the presented data set and per-
formed VLOO procedure calculating the r
i
for all points. Figure 7b shows the data
samples and the largest corresponding r
i
values. As one can see the most influential
data samples and our misclassified sample correspond to the largest r
i
values.
a) b)
Fig. 7. a) The data set with one point (0.4890, 0.4002) intentionally mislabelled; b) the data set
and largest
α
i
/C
ii
values – a potential hint for finding misclassified points.
4.4 Results on Artificial Data Set
The tests were performed on the data set tm_27749 described in 4.1. 14 permutations
were generated by randomly assigning the points to the test subset and the training
77
set. Each learning set includes 66 points: 8 points are labeled, 58 points are unla-
belled. For the same data the supervised LS-SVM classifier was created. Average
error rate of SS-LS-SVM classification results on test set 2.3%. This is twice lower
than the error rate calculated for the LS-SVM classifier based on 8 points that is equal
5.6%. The results prove that SS-LS-SVM classifier is independent of the selection of
data points to the learning set.
4.5 Pruning Procedure for Two Moons Problem
We tested the pruning procedure on two data sets tm_27749_20 and tm_94326. Ap-
plications of pruning procedure to the learning set tm_27749_20 yields in the super-
vised LS-SVM model that consists of 10 points (the original set comprised 66 points)
shown in Fig. 5. The test set classification (using pruned model) yielded in 100%
correctly classified examples.
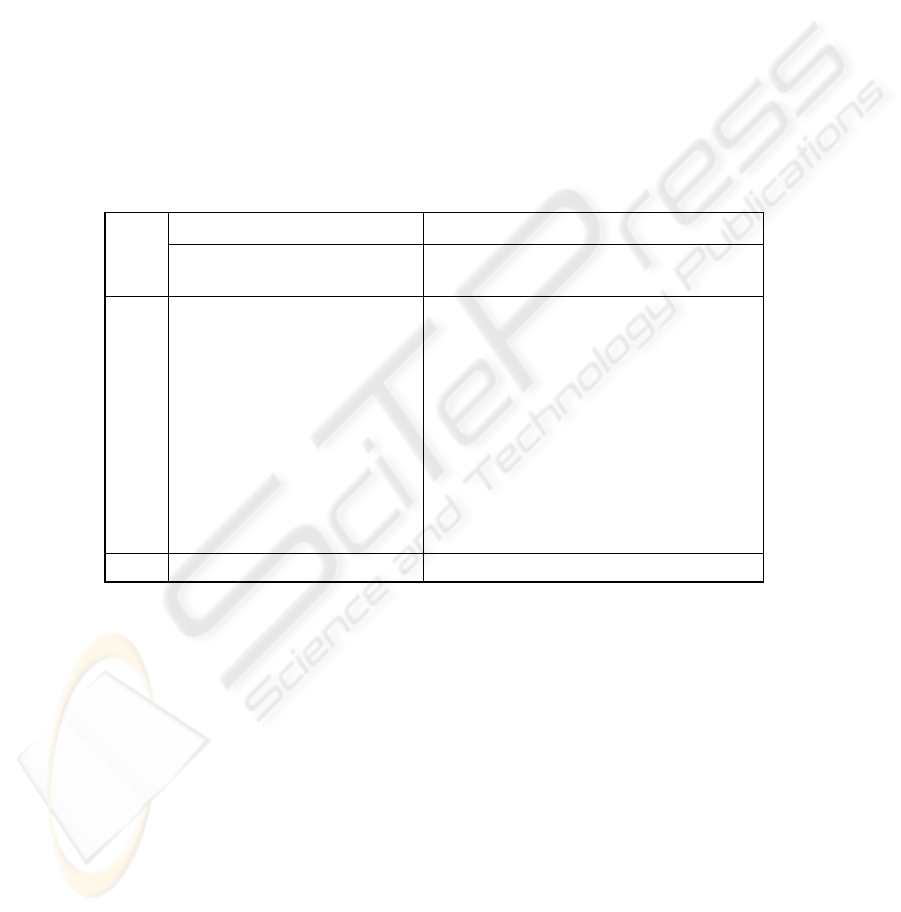
Table 1. Results of pruning procedure applied to 10 permutations of tm_94326 data sets.
original classifier pruned classifier
data
set tp tn fp fn prec recall tp tn fp fn prec recall
Model
size
01 673 653 5 3 99,26 99,56 673 653 5 3 99,26 99,56 83
02 657 667 4 6 99,39 99,10 658 671 0 5 100,00 99,25 56
03 661 664 4 5 99,40 99,25 662 664 4 4 99,40 99,40 70
04 646 677 3 8 99,54 98,78 648 678 2 6 99,69 99,08 61
05 665 661 5 3 99,25 99,55 667 663 3 1 99,55 99,85 63
06 654 668 8 4 98,79 99,39 654 668 8 4 98,79 99,39 82
07 668 654 7 5 98,96 99,26 669 653 8 4 98,82 99,41 76
08 648 674 8 4 98,78 99,39 647 674 8 5 98,78 99,23 76
09 661 659 6 8 99,10 98,80 662 659 6 7 99,10 98,95 64
10 657 663 8 6 98,80 99,10 658 663 8 5 98,80 99,25 72
Average
99,13 99,28 99,18 99,34 69
10 permutations of the tm_94326 data set were generated by randomly assigning
the points to the test subset and the training set. For every permutation the supervised
LS-SVM classifier was created using the learning set. Such model is based on 666
data points. The performance of the classifiers was checked on the corresponding test
data sets (see precision and recall values in Table 1). After application of the pruning
procedure the obtained LS-SVM model was evaluated (results are shown in Table 1)
on the corresponding test sets.
The average model after pruning comprises 69 data points (versus 666 in the orig-
inal classifier before pruning procedure). The recall and precision values obtained
from the tests of the pruned classifier are similar to the values obtained for the origi-
nal classifier. The pruning procedure can be safely applied for obtaining of much
smaller model with the same excellent properties as its original counterpart.
78

5 Medical application of SS-LS-SVM
Our study is based on the data set performed at the Warsaw University of Medicine.
It consists of 376 patients underwent the signal-averaged ECG recordings [12]. Upon
the medical diagnosis, these patients are divided into 3 groups: 100 patients with
sustained ventricular tachycardia after myocardial infarction (sVT+), 199 patients
without sustained ventricular tachycardia after myocardial infarction (sVT−) and 77
healthy persons.
The signal-averaged ECG signals were recorded using a system with a sampling
frequency of 1 kHz. Standard bipolar X,Y,Z leads were used. The time domain analy-
sis of the signal-averaged ECG was performed using FIR filter with the Kaiser win-
dow (45-150Hz) [12, 13]. For the filtered signal we calculated 9 parameters [13, 14].
Table 2 contains the results of SS-LS-SVM application to medical dataset. It con-
tains the classification results of the same dataset obtained by 3 different methods:
transductive support vector machine (TSVM), transductive least-squares support
vector machine (TLS-SVM) based on the Lagrange coefficients ranking and super-
vised SVM. The score of correct classification for SS-LS-SVM classifier based on
only 5% labelled data points is 88.4% - it indicates the advantage of VLOO criterion
vs. the Lagrange multiplier ranking. Also, this score is not much worse than that ob-
tained by SVM classifier for the full set of labelled data [14].
Table 2. Classification results of medical data (SVT+).
Method Labelled data Correct classifications
SS-LS-SVM (VLOO) 5% 88,4%
TLS-SVM (based on α)
5% 83,5%
TSVM [14] 50% 94,15%
SVM [14 ] 100% 95,21%
6 Conclusions
We present the novel approach to semi-supervised learning. The basic idea is the use
of information on influential statistics of each labelled point of the data – the leave-
one-out residual.
The virtual leave-one–out method (VLOO) enables to obtain the estimated values
of leave-one-out score for the entire training set in one step – no retraining is re-
quired.
For the semi-supervised least-squares support vector machine all calculations can
be expressed in an analytic form.
We applied our approach to the computer-aided medical diagnosis: the recognition
of sustained ventricular tachycardia after myocardial infarction. The score of success-
ful recognition (88.4 % based on 5 % of labelled cases) is meaningful.
79

References
1. 1. V.N. Vapnik: Statistical Learning Theory, Wiley Interscience, New York 1998.
2. O. Chapelle, B. Schölkopf, A. Zien: Semi-supervised Learning, MIT Press, Cambridge
2006.
3. J.A.K. Suykens and J. Vandewalle: Least squares support vector machine classifier, Neural
Processing Letters, 9 (1999), 293-300.
4. J.A.K. Suykens, T. Van Gestel, J. De Brabanter, B. De Moor, J. Vandewalle: Least Squares
Support Vector Machines, World Scientific 2002.
5. R.D. Cook, S. Weisberg, Characterization of an empirical influence function for detecting
influential cases in regression, Technometrics 22 (1980), 495-508.
6. G. Monari, G. Dreyfus: Local Overfitting Control via Leverages; Neural Computation 14
(2002), 1481-1506.
7. G.C. Cawley, N.L.C. Talbot: Fast exact leave-one-out cross-validation of sparse least-
squares support vector machines, Neural Networks 17 (2004), 1467-1475.
8. G.C. Cawley, N.L.C. Talbot: Preventing Over-fitting during Model Selection via Bayesian
Regularisation of the Hyper-Parameters, Journal of Machine Learning Research 8, (2007),
841-861.
9. F. Ojeda, J. A.K. Suykens, B. De Moor: Low rank updated LS-SVM classifier for fast
variable selection, Neural Networks 21 (2008), 437-449.
10. K. Bennett, A. Demiriz: Semi-supervised support vector machines, in M.S. Kearns, S.A.
Solla and D.A. Cohn (eds.) Advances in Neural Information Processing Systems 12, MIT
Press, Cambridge, MA, 1998, 368-374.
11. O. Chapelle, V. Sindwani, S.A. Keerthi: Optimization Techniques for Semi-Supervised
Support Vector Machines, Journal of Machine Learning Research 9, 2008, 203-233.
12. J.A. Gomes: Signal averaged electrocardiography – concepts, methods and applications.
Kluwer Academic Publishers, 1993.
13. S. Jankowski, Z. Szymański, E. Piątkowska-Janko, A. Oręziak: Improved recognition of
sustained ventricular tachycardia from SAECG by support vector machine, Anatolian
Journal of Cardiology, vol. 7 (2007), 112-115.
14.
S. Jankowski, E. Piątkowska-Janko, Z. Szymański and A. Oręziak: Transductive Support
Vector Machines for Risk Recognition of Sustained Ventricular Tachycardia and Flicker
after Myocardial Infarction, in Proceedings of the 7
th
International Workshop on Pattern
Recognition in Information Systems – PRIS 2007 (eds. Ana Fred, Anil K. Jain), June 2007,
Funchal, Portugal, 161-170.
80
