
SYNCHRONIZATION OF MODIFIED CHUA’S CIRCUITS IN STAR
COUPLED NETWORKS
O. R. Acosta del Campo
Engineering Faculty, UABC, Km. 103 Carretera Tij-Ens, Ensenada, M´exico
C. Cruz-Hern´andez
Electronics and Telecommunications Department, CICESE, Km. 107 Carretera Tij-Ens, Ensenada, M´exico
R. M. L´opez-Guti´errez , E. E. Garc´ıa-Guerrero
Engineering Faculty, UABC, Km. 103 Carretera Tij-Ens, Ensenada, M´exico
Keywords:
Hyperchaos synchronization, Modified fourth-order Chua’s circuit, Generalized Hamiltonian forms, Ob-
servers, Star coupled networks.
Abstract:
In this paper, we use Generalized Hamiltonian systems approach to synchronize dynamical networks of modi-
fied fourth-order Chua’s circuits, which generate hyperchaotic dynamics. Network synchronization is obtained
among a single master node and two slave nodes, with the slave nodes being given by observers.
1 INTRODUCTION
The synchronization problem of two chaotic oscilla-
tors has received a lot of attention in last decades,
see e.g. this example in order to achieve the high-
est quality possible (Pecora and Carroll, 1990); (Ni-
jmeijer and Mareels, 1997); (L´opez-Mancilla and
Cruz-Hern´andez, 2005); (L´opez-Mancilla and Cruz-
Hern´andez, 2008); (Cruz-Hern´andez and Nijmeijer,
2000); (Boccaleti and et. al., 2002); (Luo, 2008);
(Cruz-Hern´andez, 2004) and references therein. This
interest increases by practical applications in differ-
ent fields, particularly in secure communications, see
e.g. (Cruz-Hern´andez, 2004); (L´opez-Mancilla and
Cruz-Hern´andez, 2005); (Aguilar-Bustos and Cruz-
Hern´andez, 2008); (Cruz-Hern´andez and N.Romero-
Haros, 2008). Hyperchaotic dynamics characterized
by more than one positive Lyapunov exponent are
advantageous over simple chaotic dynamics. How-
ever, hyperchaos synchronization is a much more dif-
ficult problem, see e.g. (Aguilar-Bustos and Cruz-
Hern´andez, 2008) for two coupled oscillators.
In (Posadas-Castillo and et.al.(a), 2007) was de-
veloped an experimental study on practical realization
to synchronize dynamical networks of Chua’s circuits
globally coupled. While in recent works (Posadas-
Castillo and et. al.(b), 2007); (Posadas-Castillo and
et. al., 2008); (H. Serrano Guerrero, 2009) was ob-
tained synchronization in coupled star networks with
chaotic nodes given by Nd:YAG lasers and 3D CNNs,
respectively; by using the approach given in (Wang,
2002). Some literature devoted on synchronization
of complex networks (Manrubia and et.al., 2004);
(Pogromsky and Nijmeijer, 2001); (Wang, 2002).
Network synchronization of coupled star nodes
can be applied to transmit encrypted messages, from
a single transmitter to multiple receivers in network
communication systems, if the coupled nodes are
chaotics. The aim of this paper is to synchronize three
modified fourth-order Chua’s circuits (which exhibit
hyperchaotic behavior) studied in (Thamilmaran and
et.al., 2004) in star coupled networks via Generalized
Hamiltonian forms and observer design proposed in
(Sira-Ram´ırez and Cruz-Hern´andez, 2001). This ap-
proach presents several advantages over the existing
synchronization methods reported in the current liter-
ature.
2 PROBLEM SETTING
Consider the following set of N interconnected iden-
162
R. Acosta del Campo O., Cruz-Hernández C., E. García-Guerrero E. and M. López-Gutiérrez R. (2009).
SYNCHRONIZATION OF MODIFIED CHUA’S CIRCUITS IN STAR COUPLED NETWORKS.
In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics - Signal Processing, Systems Modeling and
Control, pages 162-167
DOI: 10.5220/0002218401620167
Copyright
c
SciTePress
tical dynamical systems
x
i
= f(x
i
) + u
i
, i = 1,2,...,N, (1)
where x
i
= (x
i1
,x
i2
,...,x
in
)
T
∈ R
n
is the state vector
and u
i
= u
i1
∈ R is the input signal of the system i,
defined by
u
i1
=c
N
∑
j=1
a
ij
Γx
j
, i = 1,2, ...,N, (2)
the constant c > 0 represents the coupling strength,
and Γ ∈ R
n×n
is a constant 0-1 matrix linking cou-
pled states.Whereas, A = (a
ij
) ∈ R
n×n
is the coupling
matrix, which represents the coupling configuration
in (1)-(2). If there is a connection between node i
and node j, then a
ij
= 1; otherwise, a
ij
= 0 for i 6= j.
Note that, if u
i1
= 0, i = 1, 2,..., N, in (1) we have a set
of N isolated dynamical systems, operating with their
own dynamics. While, if u
i1
6= 0 the set constitutes
a dynamical network and each dynamical system i is
called nodo i; and under appropiates u
i1
the dynami-
cal networks can be achieve collective behaviors. It is
clear that, the input singal u
i1
determines the kind of
coupling among nodes in the networks. The coupling
matrix for star coupled networks is given by
A =
N − 1 −1 −1 ··· −1
−1 0 0 ··· 0
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
−1 0 0 ··· 0
−1 0 0 ··· 0
(3)
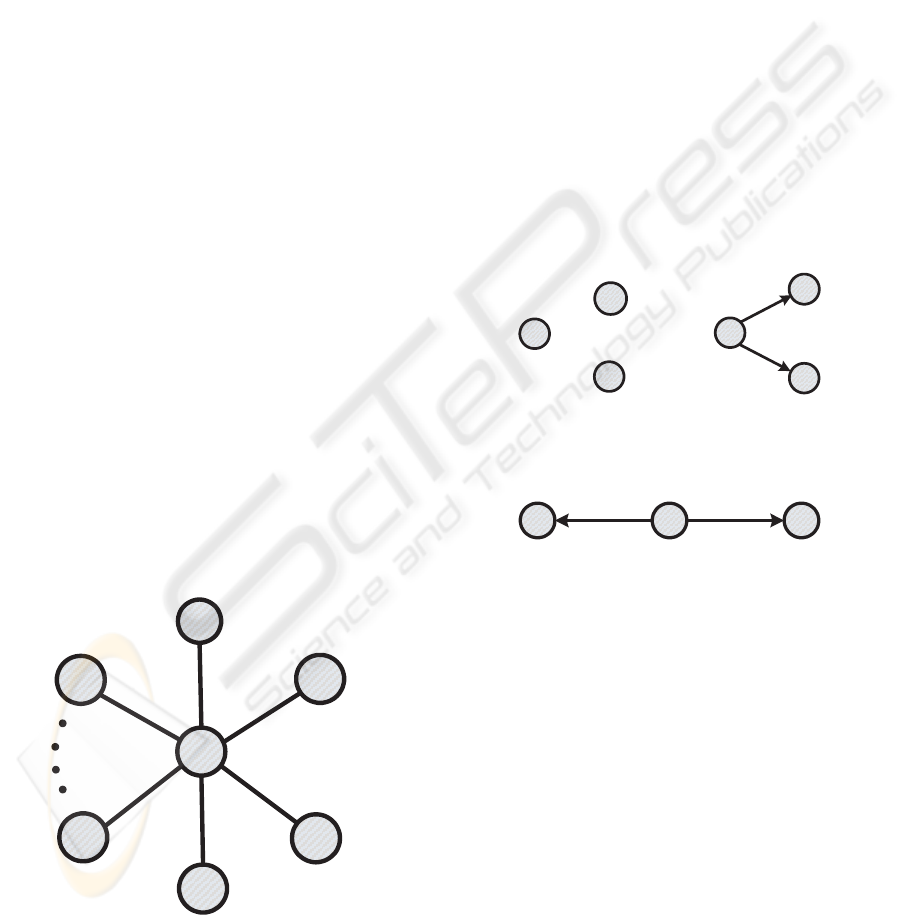
The star coupled configuration for N nodes is
shown in Fig. 1, with the common or central node
1.
2
5
1
3
4
N
6
Figure 1: Star coupled configuration with N nodes.
The complex dynamical network (1) is said to
achieve (asymptotically) synchronization, if (Wang
2002):
x
1
(t) = x
2
(t) = ... = x
N
(t) as t → ∞. (4)
The synchronization state in (1) can be an equi-
librium point, a periodic orbit or, a chaotic attrac-
tor. This paper addresses the synchronization prob-
lem of dynamical networks (1) with coupled nodes
in star topologies. In particular, by choosing a mas-
ter node with the objective of to impose a particular
collective behavior in (1). For illustrative purposes
only, we consider three isolated nodes (N = 3) to be
synchronized (which are described in Section 4), see
Fig. 2(a). In Fig. 2(b) is shown this dynamical net-
work with master node N1 and two slave nodes N2
and N3. Our objective is the synchronization of this
network, when the coupled nodes are given by mod-
ified fourth-order Chua’s circuits, to be described in
Section 4. This particular coupling topology is impor-
tant for its application to network communication sys-
tems, to transmit messages from a single transmitter
to multiple receivers (Chow T.W.W. and Ng, 2001).
N2
N3
N1
N2
N3
N1
(a)
(b)
Figure 2: (a) Three isolated nodes. (b) Star coupled network
with master node N1.
S1 M S2
y y
Figure 3: Single master node M and two slave nodes S1 and
S2 configuration.
3 SYNCHRONIZATION VIA
HAMILTONIAN FORMS
To solve the network synchronization problem stated
in previous section, we appeal to synchronization (of
two chaotic oscillators) via Hamiltonian forms and
observer design reported in (Sira-Ram´ırez and Cruz-
Hern´andez, 2001). In the sequel, we show that this
approach is appropriate to synchronize a coupled star
network with three nodes shown in Fig. 2(b). By us-
ing the proposed synchronization scheme shown in
Fig. 3, where M is given in Hamiltonian form (Eq.
(7)) and S1 and S2 being two observers for M given
by Eq. (8).
Consider the following isolated dynamical system
˙x = f(x), (5)
SYNCHRONIZATION OF MODIFIED CHUA'S CIRCUITS IN STAR COUPLED NETWORKS
163

where x(t) ∈ R
n
is the state vector, f : R
n
→ R
n
is a
nonlinear function.
In (Sira-Ram´ırez and Cruz-Hern´andez, 2001) is
reported how the dynamical system (5) can be written
in the following Generalized Hamiltonian canonical
form,
˙x = J (x)
∂H
∂x
+ S (x)
∂H
∂x
+ F (x), x ∈ R
n
, (6)
H(x) denotes a smooth energy function which is glob-
ally positive definite in R
n
. The gradient vector of H,
denoted by ∂H/∂x, is assumed to exist everywhere.
We use quadratic energy function H(x) = (1/2)x
T
Mx
with M being a, constant, symmetric positive definite
matrix. In such case, ∂H/∂x = Mx. The matrices,
J (x) and S(x) satisfy, for all x ∈ R
n
, the properties:
J (x) + J
T
(x) = 0 and S(x) = S
T
(x). The vector field
J (x)∂H/∂x exhibits the conservative part of the sys-
tem and it is also referred to as the workless part,
or work-less forces of the system; and S(x) depict-
ing the working or nonconservative part of the sys-
tem. For certain systems, S(x) is negative definite or
negative semidefinite. Thus, the vector field is con-
sidered as the dissipative part of the system. If, on the
other hand, S(x) is positive definite, positive semidef-
inite, or indefinite, it clearly represents, respectively,
the global, semi-global, and local destabilizing part
of the system. In the last case, we can always (al-
though nonuniquely) descompose such an indefinite
symmetric matrix into the sum of a symmetric nega-
tive semidefinite. matrix R(x) and a symmetric pos-
itive semidefinite matrix N(x). Finally, F(x) repre-
sents a locally destabilizing vector field.
In the context of observer design, we consider a
special class of Generalized Hamiltonian forms (to be
considered as the master node M) with linear output
map y(t), given by
˙x = J (y)
∂H
∂x
+ (I + S )
∂H
∂x
+ F (y), x ∈ R
n
, (7)
y = C
∂H
∂x
, y ∈ R
m
,
where S is a constant symmetric matrix, not necessar-
ily of definite sign. The matrix I is a constant skew
symmetric matrix, and C is a constant matrix.
We denote the estimates of the state x(t) by ˆx
i
(t),
i = 1,2 and consider the Hamiltonian energy func-
tion H( ˆx
i
) to be the particularization of H in terms
of ˆx
i
(t). Similarly, we denote by η
i
(t), i− 1, 2 the es-
timated outputs, computed in terms of the estimated
states ˆx
i
(t). The gradient vector ∂H( ˆx
i
)/∂ˆx
i
is natu-
rally, of the form M ˆx
i
with M being a, constant, sym-
metric positive definite matrix.
Two nonlinear state observers for M (7) are given
by
˙
ˆx
i
= J (y)
∂H
∂ˆx
i
+(I +S )
∂H
∂ˆx
i
+F (y)+K
i
(y−η
i
), (8)
η
i
= C
∂H
∂ˆx
i
, η
i
∈ R
m
, i = 1,2,
with ˆx
i
∈ R
n
and K
i
is the observer gain.
The state estimation errors, defined as e
i
(t) =
x(t) − ˆx
i
(t) and the output estimation error, defined
as e
iy
(t) = y(t) − η
i
(t), are governed by
˙e
i
= J (y)
∂H
∂e
i
+ (I + S − KC )
∂H
∂e
i
, e
i
∈ R
n
, (9)
e
iy
= C
∂H
∂e
i
, e
iy
∈ R
m
, i = 1,2,
where the vectors ∂H/∂e
i
actually stands, with some
abuse of notation, for the gradient vector of the
modified energy functions, ∂H(e
i
)/∂e
i
= ∂H/∂x −
∂H/∂ˆx
i
= M(x − ˆx
i
) = Me
i
. We set, when needed,
I + S =W .
A necessary and sufficient condition for global
asymptotic stability to zero of the estimation errors
(9) is given by the following theorem.
Theorem 1 (Sira-Ram´ırez and Cruz-Hern
´
andez,
2001). The state x(t) of the master node M (7) can
be globally, exponentially, asymptotically estimated,
by the states ˆx
i
(t), i = 1,2 of the observers (8) if and
only if, there exist constant matrices K
i
such that the
symmetric matrices
[W − K
i
C ] + [W − K
i
C ]
T
= [S − K
i
C ]+[S − K
i
C ]
T
= 2
S −
1
2
(K
i
C + C
T
K
T
i
)
are negative definite.
4 HYPERCHAOTIC CHUA’S
CIRCUIT LIKE NODE
Consider the modified fourth-order Chua’s circuit de-
scribed by (Thamilmaran and et.al., 2004):
˙x
1
= α
1
(x
3
− f (x
1
)),
˙x
2
= −α
2
x
2
− x
3
− x
4
,
˙x
3
= β
1
(x
2
− x
1
− x
3
),
˙x
4
= β
2
x
2
,
(10)
with nonlinear function given by
f (x
1
) = bx
1
+
1
2
(a− b)(|x
1
+ 1|− |x
1
− 1|). (11)
With the paramerter values: α
1
= 2.1429, α
2
=
−12.83, β
1
= 0.0393, β
2
= 0.0015, a = −0.0299, and
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
164

b = 1.995 the modified Chua’s circuit (10)-(11) ex-
hibits hyperchaotic behavior, with two positive Lya-
punov exponents. By using the initial conditions
x(0) = (1.1,0.1,−0.5,0.01), Figs. 1, 2, 3, and 4 show
the hyperchaotic attractors x
1
vs x
2
, x
2
vs x
3
, x
3
vs x
4
,
and x
1
vs x
4
, respectively.
−4 −3 −2 −1 0 1 2 3 4
−1.5
−1
−0.5
0
0.5
1
1.5
Figure 4: Hyperchaotic attractor projected onto the (x
1
, x
2
)-
plane.
−4 −3 −2 −1 0 1 2 3 4
−0.8
−0.6
−0.4
−0.2
0
0.2
0.4
0.6
0.8
Figure 5: Hyperchaotic attractor projected onto the (x
2
, x
3
)-
plane.
−0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8
−0.2
−0.15
−0.1
−0.05
0
0.05
0.1
0.15
Figure 6: Hyperchaotic attractor projected onto the (x
3
, x
4
)-
plane.
−0.2 −0.15 −0.1 −0.05 0 0.05 0.1 0.15
−1.5
−1
−0.5
0
0.5
1
1.5
Figure 7: Hyperchaotic attractor projected onto the (x
1
, x
4
)-
plane.
Next, we show the arrangement for star dynami-
cal network by using as coupled node to hyperchaotic
Chua’s circuit defined by (10)-(11).
5 SYNCHRONIZATION OF
HYPERCHAOTIC CHUA’S
CIRCUITS IN A STAR
NETWORK
In this section, we show the synchronization of three
hyperchaotic Chua’s circuits in a star coupled net-
work, via Generalized Hamiltonian forms and ob-
server design proposed in (Sira-Ram´ırez & Cruz-
Hern´andez 2001). Firstly, we rewrite the modified
fourth-order Chua’s circuit (10)-(11) for the master
node as follows.
Taking as Hamiltonian energy function to
H (x) =
1
2
1
α
1
x
2
1
+ x
2
2
+
1
β
1
x
2
3
+
1
β
2
x
2
4
. (12)
Modified fourth-order Chua’s circuit (10)-(11) in
Generalized Hamiltonian form (master node, M) ac-
cording to Eq. (7) is given by
˙x
1
˙x
2
˙x
3
˙x
4
=
0 0 α
1
β
1
0
0 0 −β
1
−β
2
−α
1
β
1
β
1
0 0
0 β
2
0 0
∂H
∂x
+ (13)
0 0 0 0
0 −α
2
0 0
0 0 −β
2
1
0
0 0 0 0
∂H
∂x
+
−α
1
f (x
1
)
0
0
0
.
The destabilizing vector field calls for x
1
(t) to be
used as the output y(t), of the master node M (13).
The matrices C, S, and I are given by
C
T
=
α
1
0
0
0
, S =
0 0 0 0
0 −α
2
0 0
0 0 −β
2
1
0
0 0 0 0
,
I =
0 0 α
1
β
1
0
0 0 −β
1
−β
2
−α
1
β
1
β
1
0 0
0 β
2
0 0
.
Next, we design two state observers (slave nodes S1
and S2, see Fig. 3) for master node (13). The first
nonlinear state observer for the Generalized Hamilto-
nian system (13) (according to Eq. (8) as slave node
SYNCHRONIZATION OF MODIFIED CHUA'S CIRCUITS IN STAR COUPLED NETWORKS
165

S1 is given by
˙
ˆx
11
˙
ˆx
12
˙
ˆx
13
˙
ˆx
14
=
0 0 α
1
β
1
0
0 0 −β
1
−β
2
−α
1
β
1
β
1
0 0
0 β
2
0 0
∂H
∂ˆx
+ (14)
0 0 0 0
0 −α
2
0 0
0 0 −β
2
1
0
0 0 0 0
∂H
∂ˆx
+
−α
1
f (x
1
)
0
0
0
+
k
11
k
12
k
13
k
14
e
1y
,
η
1
= ˆx
11
,
the second state observer (slave S2) is described by
˙
ˆx
21
˙
ˆx
22
˙
ˆx
23
˙
ˆx
24
=
0 0 α
1
β
1
0
0 0 −β
1
−β
2
−α
1
β
1
β
1
0 0
0 β
2
0 0
∂H
∂ˆx
+ (15)
0 0 0 0
0 −α
2
0 0
0 0 −β
2
1
0
0 0 0 0
∂H
∂ˆx
+
−α
1
f (x
1
)
0
0
0
+
k
21
k
22
k
23
k
24
e
2y
,
η
2
= ˆx
21
,
where e
1y
= x
1
− ˆx
11
(e
11
= y − η
1
) and e
2y
= x
1
−
ˆx
21
(e
21
= y− η
2
). From master node (13) and slave
nodes (14) and (15), we have that the synchronization
error dynamics among the master node and two slave
nodes (observers) is governed by
˙e
i1
˙e
i2
˙e
i3
˙e
i4
=
0
k
i2
α
1
2
γ
i
k
i4
α
1
2
−
k
i2
α
1
2
0 −β
1
−β
2
−γ
i
β
1
0 0
−
k
i4
α
1
2
β
2
0 0
∂H
∂e
i
+
−k
i1
α
1
k
i2
α
1
2
−
k
i3
α
1
2
k
i4
α
1
2
−
k
i2
α
1
2
−α
2
0 0
−
k
i3
α
1
2
0 −β
2
1
0
−
k
i4
α
1
2
0 0 0
∂H
∂e
i
(16)
where γ
i
= α
1
β
1
+
k
i3
α
1
2
. Where the synchronization
errors are defined by e
1
and e
2
among master M
and slaves 1 and 2, respectively. One may now
choose the observer gains K
i
= (k
i1
,k
i2
,k
i3
,k
4i
)
T
, i =
1,2 in order to guarantee asymptotic exponential sta-
bility to zero of the synchronization errors e
i
(t) =
(e
i1
(t),e
i2
(t),e
i3
(t),e
i4
(t)), i = 1, 2 as will be shown
in the next section.
6 SYNCHRONIZATION
CONDITIONS
Now, we examine the stability of the synchroniza-
tion errors (16) for the network constructed with mas-
ter (13) and two slaves (14) and (15), with modi-
fied Chua’s circuits as coupled nodes. Thus, we in-
voke Theorem 1, which guarantees global asymp-
totic stability to zero of e
i
(t), i = 1,2. In par-
ticular, for modified Chua’s circuit, the matrices
2
S −
1
2
(K
i
C + C
T
K
T
i
)
, i = 1,2 shown in Theorem
1, are give by
−2k
i1
α
1
−k
i2
α
1
−k
i3
α
1
−k
i4
α
1
−k
i2
α
1
−2α
2
0 0
−k
i3
α
1
0 −2β
2
1
0
−k
i4
α
1
0 0 0
, i = 1,2
(17)
by applying the Sylvester’s Criterion -which provides
a test for negative definite of a matrix- thus, we have
that the mentioned matrices will be negative defi-
nite matrices, if we choose K
i
= (k
i1
,k
i2
,k
i3
,k
i4
)
T
,
i = 1, 2 such that the following conditions are satis-
fied:
k
i1
≤ 1, (18)
4k
i1
α
1
α
2
− k
2
i2
α
2
1
≥ 0,
2
α
1
β
2
1
α
1
k
2
i2
− 4k
i1
α
2
+ k
2
i3
α
2
1
α
2
≥ 0,
k
i4
= 0.
We have used K
1
= (3.3,1.5,0.39,0)
T
and
K
2
= (2.3,1,0.3,0)
T
with initial conditions:
for M, x(0) = (1.1,0.1,−0.5,0.01) and for
S1, ˆx
1
(0) = (0.5,0.3,−0.4,0) and for S2,
ˆx
2
(0) = (1,0, −0.2,0.04). Fig. 8 shows the
synchronization among master node (13) and two
slave nodes (14) and (15).
−1.5 −1 −0.5 0 0.5 1 1.5
−2
0
2
Master vs Slave 1
X
11
X
1
−1.5 −1 −0.5 0 0.5 1 1.5
−2
0
2
Master vs Slave 2
X
21
X
1
−3 −2 −1 0 1 2 3 4
−5
0
5
X
12
X
2
−3 −2 −1 0 1 2 3 4
−5
0
5
X
22
X
2
−0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6
−1
0
1
X
13
X
3
−0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6
−1
0
1
X
23
X
3
−0.06 −0.04 −0.02 0 0.02 0.04 0.06 0.08
−0.1
0
0.1
X
14
X
4
−0.06 −0.04 −0.02 0 0.02 0.04 0.06 0.08
−0.1
0
0.1
X
24
X
4
Figure 8: Complete synchronization among states of hyper-
chaotic master node M and slave nodes S1 and S2.
7 CONCLUSIONS
In this paper, we have presented multiple synchro-
nization of coupled modified fourth-order Chua’s cir-
cuit, in particular by using star coupled networks.
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
166

We have achieve synchronization of three hyper-
chaotic Chua’s circuit (used as fundamental node) in
star complex networks, via Generalized Hamiltonian
forms and observer design considering a single mas-
ter node and two slave nodes. This result is particu-
larly interesting given its application in communica-
tion network systems, where is required that a single
sender transmits simultaneously information to many
receivers via a public channel.
ACKNOWLEDGEMENTS
This work was supported by CONACYT, M´exico un-
der Research Grant Nos. J49593-Y, and P50051-Y.
REFERENCES
Aguilar-Bustos, A. and Cruz-Hern´andez, C. (2008). Syn-
chronization of discrete-time hyperchaotic systems:
An application in communications. In Chaos, Solitons
and Fractals. INSTICC Press.
Boccaleti, S. and et. al. (2002). The synchronization of
chaotic systems. In Physics Reports, 336:1.
Chow T.W.W., F. J.-C. and Ng, K. (2001). Chaotic network
synchronization with applications to communication.
In J. Commun. Syst., 14, 217-30.
Cruz-Hern´andez, C. (2004). Synchronization of time-delay
chua’s oscillator with application to secure communi-
cation. In Nonlinear Dyn. Syst. Theory 4(1), 1-13.
Cruz-Hern´andez, C. and Nijmeijer, H. (2000). Synchroniza-
tion through filtering. In Int. J. Bifurc. Chaos 10 (4),
763-775.
Cruz-Hern´andez, C. and N.Romero-Haros (2008). Commu-
nicating via synchronized time-delay chua’s circuits.
In Commun. Nonlinear Sci. Numer. Simul.;13(3), 645-
59.
H. Serrano Guerrero, a. e. a. (2009). Synchronization in
star coupled networks of 3d cnns and its application
in communications. In submitted to chapter in Evo-
lutionary Design of Intelligent Systems in Modeling’,
Simulation and Control. Springer-Verlag.
L´opez-Mancilla, D. and Cruz-Hern´andez, C. (2005). Out-
put synchronization of chaotic systems: model-
matching approach with application to secure commu-
nication. In Nonlinear Dyn. Syst. Theory 5(2), 141-
156.
L´opez-Mancilla, D. and Cruz-Hern´andez, C. (2008). Out-
put synchronization of chaotic systems under nonvan-
ishing perturbations. In Chaos, Solitons and Fractals
37, 1172-1186.
Luo, A. C. J. (2008). A theory for synchronization of dy-
namical systems. In Commun. Nonlinear Sci. Numer.
Simulat., doi:10.1016/j.cnsns.2008.07.002.
Manrubia, S. and et.al. (2004). Emergence of dynamical or-
der, synchronization phenomena in complex systems.
In World Scientific, Lecture Notes in Complex Systems
Vol. 2, Singapore.
Nijmeijer, H. and Mareels, I. (1997). An observer looks at
synchronization. In IEEE Trans. Circ. Syst. I 44(10),
882-890.
Pecora, L. and Carroll, T. (1990). Synchronization in
chaotic systems. In Phys. Rev. Lett. 64, 821-824.
Pogromsky, Y. A. and Nijmeijer, H. (2001). Cooperative os-
cillatory behavior of mutually coupled dynamical sys-
tems. In IEEE Trans. Circ. Syst. I 48(2), 152-162.
Posadas-Castillo, C. and et. al. (2008). Synchronization in a
network of chaotic solid-state nd:yag lasers. In Procs.
of the 17th World Congress IFAC, Seoul, Korea, July
6-11, 1565-1570.
Posadas-Castillo, C. and et. al.(b) (2007). Lecture Notes
in Artificial Intelligence, No. 4529, Synchronization
in arrays of chaotic neural networks, in Foundations
of Fuzzy Logic and Soft Computing. Springer-Verlag,
Berlin Heidelberg, 1st edition.
Posadas-Castillo, C. and et.al.(a) (2007). Experimental re-
alization of synchronization in complex networks with
chua’s circuits like nodes. In Chaos, Solitons and
Fractals, In press doi:10.1016/j.chaos.2007.09.076.
Sira-Ram´ırez, H. and Cruz-Hern´andez, C. (2001). Synchro-
nization of chaotic systems: A generalized hamilto-
nian systems approach. In Int. J. Bifurc. Chaos 11(5),
1381-1395.
Thamilmaran, K. and et.al. (2004). Hyperchaos in a mod-
ified canonical chua’s circuit. In Int. J. Bifur. Chaos.
14(1), 221243.
Wang, X. F. (2002). Complex networks: Topology, dynam-
ics and synchronization. In Int. J. Bifurc. Chaos 12(5),
885-916.
SYNCHRONIZATION OF MODIFIED CHUA'S CIRCUITS IN STAR COUPLED NETWORKS
167
