Order-based Freight Transportation Operation
Planning in Railway Networks
Davide Anghinolfi, Massimo Paolucci, Simona Sacone and Silvia Siri
Dept. of Communication, Computer and System Sciences
Via Opera Pia 13, 16145 Genova, University of Genova, Italy
Abstract. In this paper we propose a planning procedure for serving freight
transportation requests (i.e. orders) in a railway network in which the terminals
are provided with innovative transfer systems. We consider a consolidated trans-
portation system where different customers make their own requests for moving
boxes (either containers or swap bodies) between different origins and destina-
tions, with specific requirements on delivery times. The decisions to be taken
concern the path (and the corresponding sequence of trains) that each box fol-
lows over the network and the assignment of boxes to train wagons, taking into
account that boxes can change more than one train during their path and that train
timetables are fixed. This planning problem is divided in two sequential phases:
a preprocessing analysis for which a specific algorithm is provided and an opti-
mization phase for which a mathematical programming formulation is proposed.
The effectiveness of the proposed procedure is tested on a set of randomly gener-
ated instances.
1 Introduction
This work deals with the definition of a planning procedure for a centralized decision
maker that must provide a transportation service to different customers by using an
available railway infrastructure. The transportation demand from customers is given
by a set of orders characterized by a certain number of boxes (in general of different
types), an origin, a destination and time delivery specifications. The transportation offer
is a railway network in which the number of trains, their schedules and paths are fixed.
This railway network is innovative since the terminals are supposed to be equipped
with rapid (horizontal) transfer systems for containers and swap bodies. This implies
that a container can move from an origin to a destination terminal by changing different
trains on its path, as it happens to passengers. Moreover, a peculiar characteristic of
the proposed approach is that boxes of the same order can follow different paths on the
network.
In the literature it is possible to find many planning approaches for intermodal trans-
portation systems involving modelling and optimization techniques, that can be classi-
fied according to the considered planning level, i.e. strategic, tactical and operational,
as it is deeply described in [1] and [2]. The problem faced in this paper can be consid-
ered as an operational problem combining two important decision aspects. The former
Anghinolfi D., Paolucci M., Sacone S. and Siri S. (2009).
Order-based Freight Transportation Operation Planning in Railway Networks.
In Proceedings of the 3rd International Workshop on Intelligent Vehicle Controls & Intelligent Transportation Systems, pages 27-36
Copyright
c
 SciTePress

decision concerns which path a box must follow on the network and in which terminals
it must change the train. This aspect is also treated in tactical problems, i.e. service net-
work design problems, as described in [3], in which the optimal paths are searched for
aggregated cargo flows instead of single load units as in the present paper. The latter
decision aspect deals with the assignment of boxes to wagons of the trains selected to
transport them. This aspect has been treated in [4], where rapid transshipment yards
are considered as in the present paper; moreover, in [5] a load planning problem, i.e.
the assignment of containers to train slots, is treated. In addition, differently from [6]
and [7], we assume the train scheduling and routing as given and fixed. Therefore, the
problem described in this paper provides a new approach for a planning procedure in
a railway network with rapid rail-rail transfers, in which, for each box, the decisions
to be taken concern the route to cover, the trains and the wagons to be placed in. Even
though all these aspects have been already treated in various works that can be found in
the literature, the main novelty of this paper (a preliminary version of this work can be
found in [8]) stands in the consideration of all these decision aspects together.
The planning procedure is divided in two sequential phases, so that the output data
of the former phase are input data of the latter. In the former phase, called preprocessing,
each order is considered separately: by taking into account the network structure, the
timetables and routes of trains, the origin, destination and time requirements of orders,
all the sequences of trains that can be used for serving the boxes of the considered
order are computed. In the latter phase, called optimal assignment, the assignment of
each box to a train sequence and to a wagon of the trains composing the sequence is
obtained by considering all the sequences of trains for each order and by taking into
account some specific data about boxes and wagons. This is the result of a specific
mathematical programming problem.
These two phases of the proposed planning procedure are described, respectively, in
Section 2 and in Section 3. The effectivenessof this procedure is then verified with some
experimental tests reported in Section 4. The conclusions and future developments of
the work are then described in Section 5.
2 Preprocessing
The railway network is described by means of a directed graph G = (N , L) where
nodes represent railway terminals and links are railway connections between terminals.
The input data of the preprocessing are referred to nodes of the network, a set R of
trains and a set O of orders:
δ
n
fixed cost for handling one box at terminal n ∈ N
ρ
n
hourly cost for the storage of one box at terminal n ∈ N
Nl
r
number of links covered by train r ∈ R
L
r
vector 1 × N l
r
indicating the path (as a sequence of links) covered by train r ∈ R
t
dep
r,l
expected departure time on link l inL
r
for train r ∈ R
t
arr
r,l
expected arrival time on link l in L
r
for train r ∈ R
n
O
o
origin railway terminal for order o ∈ O
n
D
o
destination railway terminal for order o ∈ O
t
in
o
time instant in which goods of order o ∈ O are ready at the origin node

t
∗
min,o
minimum delivery time instant for order o ∈ O
t
∗
max,o
maximum delivery time instant for order o ∈ O
Np
o
number of alternative paths connecting the origin and destination nodes of order
o ∈ O
Nl
o,p
number of links of path p = 1, . . . , Np
o
of order o ∈ O
L
o,p
vector 1 × N l
o,p
indicating the sequence of links of path p = 1, . . . , Np
o
of order
o ∈ O
ζ
o,p
cost of path p = 1, . . . , N p
o
of order o ∈ O (this cost is related to the priority of
path p in comparison with the other paths of the same order; we set ζ
o,p
= 1 for the
primary path, ζ
o,p
= 1.1 for the secondary path, and so on)
N
1
o,p
N
2
o,p
N
3
o,p
L
1,2
o,p
L
2,3
o,p
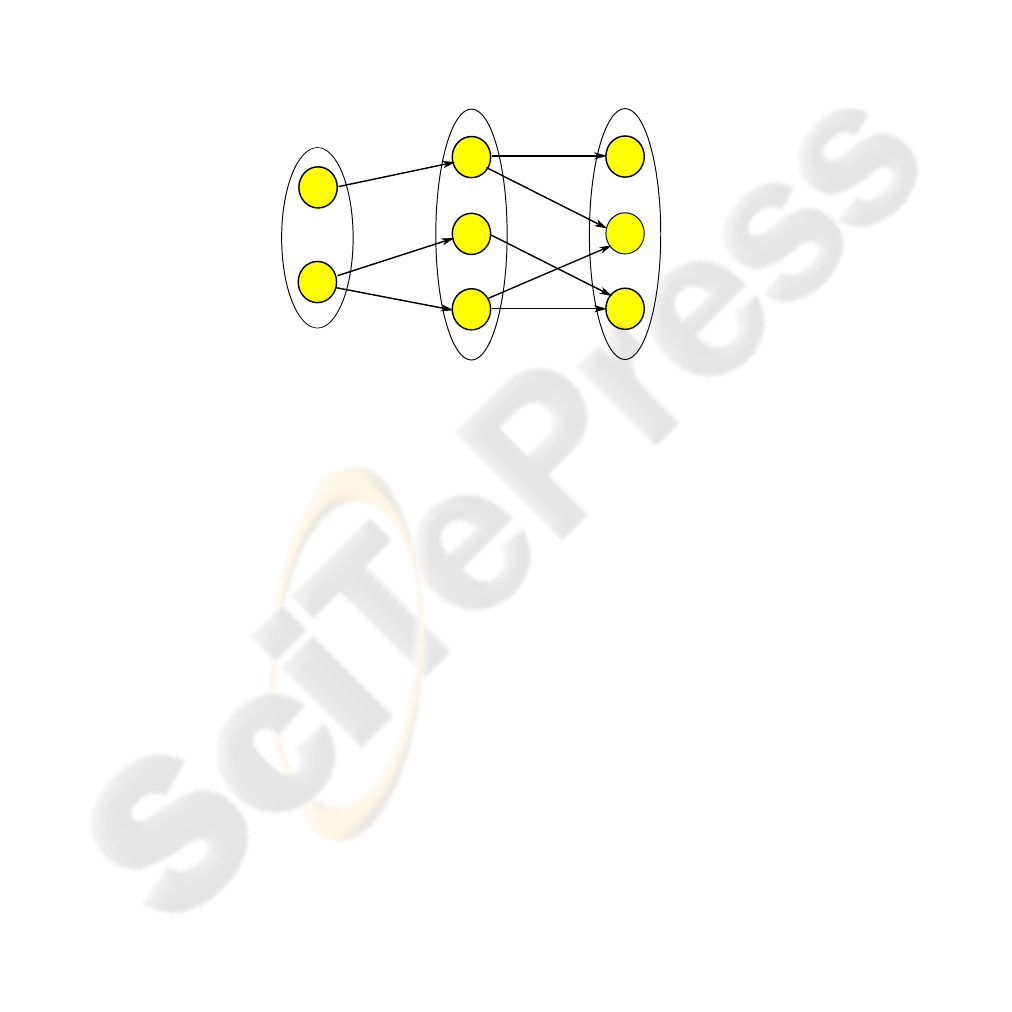
Fig.1. Graph G
o,p
in case Nl
o,p
= 3.
The preprocessing phase identifies all the feasible train sequences for each order by
analysing one order at a time and, for each order,each path singularly. Then, proceeding
backward from the last link of a path, i.e. the last element of vector L
o,p
, to the first
link, it is necessary to verify whether a train can be used on the considered link. For
the last link of a path this is obtained finding all trains arriving in time with respect to
the maximum delivery time t
∗
max,o
and leaving not before the time t
in
o
in which goods
are ready at the origin. Going backward, considering the trains selected for a link, we
search for those trains in the previous link such that the time connections are respected
and, again, the departure time is not before t
in
o
.
For each order and for each of the N p
o
paths of the order, this procedure leads
to the creation of a graph composed of N l
o,p
partitions. Let us define this graph as
G
o,p
= (N
o,p
, L
o,p
). As shown for example in Fig. 1 for N l
o,p
= 3, we denote the
set of nodes in the different partitions as N
i
o,p
, i = 1, . . . Nl
o,p
, and the set of links as
L
i,i+1
o,p
, i = 1, . . . , N l
o,p
− 1. Each node in N
i
o,p
is a feasible train in the i-th railway
link of path p of order o and each link of L
i,i+1
o,p
represents the fact that the connected
nodes (i.e. trains) are adjacent in a train sequence. For this reason, after creating this
graph, all the train sequences are obtained as all the possible paths in this graph. In
the following, the backward procedure for the construction of graph G
o,p
for order o
and for a given path p ∈ {1, . . . , Np
o
} is described. In this procedure the constant ∆t

represents the time necessary for a box unloaded from a train in a terminal to be ready
for being loaded on another train, and R
l
represents the set of trains covering link l.
initialize m = Nl
o,p
;
set l as the last link of the path;
foreach r in R
l
do
if t
arr
r,l
≤ t
∗
max,o
and t
dep
r,l
≥ t
in
o
then
add r in N
m
o,p
;
end
end
foreach ρ in N
m
o,p
do
set t
∗
ρ,m
= t
dep
ρ,l
− ∆t
end
for i=m-1 to 1 do
set l as the i-th link of the path;
foreach ρ in N
i+1
o,p
do
foreach r in R
l
do
if t
arr
r,l
≤ t
∗
ρ,m
and t
dep
r,l
≥ t
in
o
then
add r in N
i
o,p
;
add link (r, ρ) in L
i,i+1
o,p
;
end
end
foreach ρ in N
i
o,p
do
set t
∗
ρ,i
= t
dep
ρ,l
− ∆t
end
end
end
After the completion of the backward procedure constructing the graph G
o,p
, a for-
ward procedure is applied which, for each order o and for each path p, p = 1, . . . , Np
o
,
identifies N s
o,p
train sequences. Each train sequence S
o,p,s
, s = 1, . . . , N s
o,p
, is a
vector 1 × Nl
o,p
listing the trains for each link of path p for order o. While proceed-
ing forward in the graph, the cost associated with each train sequence is computed. For
each train sequence, let ϕ
n
o,p,s
∈ {0, 1 } denote whether the box changes train in termi-
nal n ∈ N (without considering the origin and destination terminal) and H
n
o,p,s
denote
the time (in hours) in which a box is stored at terminal n ∈ N . Then the cost C
o,p,s
for
the sequence s of path p for order o is computed as follows:
C
o,p,s
= ζ
o,p
n
X
i=1

ϕ
n
o,p,s
· δ
n
+ H
n
o,p,s
· ρ
n

(1)
Finally, we need to define the following sets to state the planning problem described
in Section 3:
– R
o,p,s
, p = 1, . . . , Np
o
, s = 1, . . . , Ns
o,p
, is the set of trains included in sequence
s of path p for order o;

– S
U
o,p,n,r
, p = 1, . . . , Np
o
, n ∈ N , r ∈ R
n
is the set gathering the indices of
sequences of path p for order o so that boxes are unloaded from train r at node n
(by definition, it is S
U
o,p,n,r
⊆ {1, . . . , N s
o,p
});
– S
L
o,p,n,r
, p = 1, . . . , N p
o
, n ∈ N , r ∈ R
n
is analogous to the previous set but
refers to loading operations;
– S
T
o,p,n,r
, p = 1, . . . , Np
o
, n ∈ N , r ∈ R
n
refers to transfer operations (i.e. trains
that pass a given node and do not involve any loading or unloading operations).
3 Optimal Assignment
The definition of the optimization problem is based on the output data of the prepro-
cessing phase as well as the following input data:
Nb
o
number of boxes associated with order o ∈ O
π
o,b
length of box b = 1, . . . , Nb
o
of order o ∈ O
ω
o,b
weight of box b = 1, . . . , Nb
o
of order o ∈ O
Ω
r
maximum bearable weight for train r ∈ R
K
r
cost related to the use of train r ∈ R
Nw
r
number of wagons of train r ∈ R
Ω
r,w
maximum bearable weight of wagon w = 1 , . . . , Nw
r
of train r ∈ R
Π
r,w
length of wagon w = 1, . . . , Nw
r
of train r ∈ R
σ
n
maximum number of handling operations (loading and unloading) for each train
at terminal n ∈ N (this term depends on the handling capacity provided by each
terminal)
The problem decision variables are listed in the following:
– y
o,b,p,s
∈ {0, 1}, o ∈ O, b = 1, . . . , Nb
o
, p = 1, . . . , N p
o
, s = 1, . . . , N s
o,p
,
assuming value 1 if box b of order o is assigned to sequence s of path p, otherwise
equal to 0;
– x
o,b,p,s,r,w
∈ {0, 1}, o ∈ O, b = 1, . . . , Nb
o
, p = 1, . . . , Np
o
, s = 1, . . . , N s
o,p
,
r ∈ R
o,p,s
, w = 1, . . . , Nw
r
, assuming value 1 if box b of order o is assigned to
wagon w of train r in sequence s of path p, otherwise equal to 0;
– z
r
∈ {0, 1}, r ∈ R, assuming value 1 if train r is used, otherwise equal to 0.
The planning problem is formulated as a 0/1 linear programming (LP) problem
whose objectivefunction considers the cost terms associated with train sequences (com-
puted in the preprocessing phase) and train costs.
Problem 1.
min
y
o,b,p,s
x
o,b,p,s,r,w
z
r
X
o∈O
Nb
o
X
b=1
Np
o
X
p=1
Ns
o,p
X
s=1
C
o,p,s
· y
o,b,p,s
+
X
r∈R
K
r
· z
r
(2)
subject to
Np
o
X
p=1
Ns
o,p
X
s=1
y
o,b,p,s
= 1 o ∈ O b = 1, . . . , N b
o
(3)

Nw
r
X
w=1
x
o,b,p,s,r,w
= y
o,b,p,s
o ∈ O b = 1, . . . , N b
o
p = 1, . . . , N p
o
s = 1, . . . , Ns
o,p
r ∈ R
o,p,s
(4)
X
o∈O
Nb
o
X
b=1
Np
o
X
p=1
X
s∈(S
L
o,p,n,r
∪S
T
o,p,n,r
)
Nw
r
X
w=1
ω
o,b
x
o,b,p,s,r,w
≤ Ω
r
z
r
n ∈ N r ∈ R
n
(5)
X
o∈O
Nb
o
X
b=1
Np
o
X
p=1
X
s∈(S
L
o,p,n,r
∪S
T
o,p,n,r
)
π
o,b
x
o,b,p,s,r,w
≤ Π
r,w
n ∈ N r ∈ R
n
w = 1, . . . , N w
r
(6)
X
o∈O
Nb
o
X
b=1
Np
o
X
p=1
X
s∈(S
L
o,p,n,r
∪S
T
o,p,n,r
)
ω
o,b
x
o,b,p,s,r,w
≤ Ω
r,w
n ∈ N r ∈ R
n
w = 1, . . . , N w
r
(7)
X
o∈O
Nb
o
X
b=1
Np
o
X
p=1
X
s∈(S
L
o,p,n,r
∪S
U
o,p,n,r
)
Nw
r
X
w=1
x
o,b,p,s,r,w
≤ σ
n
n ∈ N r ∈ R
n
(8)
y
o,b,p,s
∈ {0, 1}
o ∈ O b = 1, . . . , Nb
o
p = 1, . . . , Np
o
s = 1, . . . , Ns
o,p
(9)
x
o,b,p,s,r,w
∈ {0, 1} o ∈ O b = 1, . . . , N b
o
p = 1, . . . , N p
o
s = 1, . . . , Ns
o,p
r ∈ R
o,p,s
w = 1, . . . , Nw
r
(10)
z
r
∈ {0, 1} r ∈ R (11)
Constraints (3) impose that each box of each order is assigned to one and only one
train sequence, while (4) impose the relation between y
o,b,p,s
and x
o,b,p,s,r,w
variables.
Constraints (5) concern the maximum weight that each train can bear and define the
relation between x
o,b,p,s,r,w
and z
r
variables. Constraints (6) and (7) impose that boxes
assigned to wagons must be compatible with the wagon length and the weight limita-
tions for each wagon. Constraints (8) regard the maximum handling operations that can
be performed for each train at a given terminal.
4 Experimental Results
We coded the preprocessing analysis and the optimization procedure in C♯ using Cplex
11.0 as 0/1 LP solver. Then we ran some experiments to evaluate the performance of the

proposed planning approach, after having introduced in the statement of Problem 1 the
possibility of not assigning all the boxes. To do this, we transformed equality constraints
(3) into not greater or equal to inequalities and we added in the cost function the penalty
term
M ·
X
o∈O
Nb
o
X
b=1


1 −
Np
o
X
p=1
Ns
o,p
X
s=1
y
o,b,p,s


in order to minimize the number of possibly not assigned boxes (here M is a constant
much larger than any other constant in the objective function).
We analysed two different scenarios for the network and trains, one called Small
scenario (7 nodes, 20 links and 56 trains) and the other called Large scenario (10 nodes,
34 links and 98 trains). The considered planning horizon is one week, 2 types of wagons
and 13 typologies of boxes are taken into account, each train covers either 2 or 3 links
and has a number of wagons between 6 and 10. Data about orders were randomly gen-
erated: in particular, we generated 6 groups of 5 instances, called SmallA (20 orders and
3÷5 boxes per order), SmallB (30 orders and 4÷5 boxes per order), SmallC (40 orders
and 5÷7 boxes per order) for the small scenario, whereas LargeA (40 orders and 2÷4
boxes per order), LargeB (50 orders and 4÷6 boxes per order), LargeC (60 orders and
6÷8 boxes per order) for the large scenario. We applied the preprocessing computation
and, then, we solved these instances imposing the time limit of 2h for the Cplex solver.
The tests were executed on a 2.8 GHz Pentium 4 computer with 2 GB of RAM.
In Table 1 we report the number of variables of the 0/1 LP formulation, the CPU
time needed to solve the instance (in seconds), the percentage optimality gap, the num-
ber of not assigned boxes in the solution and the number of boxes that the solver proved
that cannot be assigned in the optimal solution. We only show the computation time of
Cplex solver because the computation time for preprocessing and model building can
be considered irrelevant as it was always lower than 30 seconds. Note that, having pe-
nalized in the objective function the choice of not serving boxes, the last two columns
in Table 1 are obtained as
NotAssSol =

Objective
M

NotAssP rov =

Lowe rBound
M

where LowerBound denotes the value of the best lower bound found by the solver. We
computed the optimality gap as
OptimGap =
(Objective mod M ) − (L owerBound mod M )
Objective mod M
· 100
where the operator mod finds the remainder of the integer division between two num-
bers. In this way Objective mod M = Objective and LowerBound mod M =
Lowe rBound, when NotAssSol = 0 and N otAssP rov = 0 , but when not all the
boxes are assigned, i.e., N otAssSol 6= 0 and NotAssP rov 6= 0, the gap is computed
by considering the objective function and the lower bound without the penalization
terms.
Analysing the results in Table 1, we can note that the instances corresponding to
the small scenario are solved in a satisfactory way, showing increasing difficulty form

Table 1. Cplex performances.
Instance ID No. of variables CPU time OptimGap NotAssSol NotAssP rov
SmallA1 16376 2216 opt. 0 0
SmallA2 25865 7200 7.83 0 0
SmallA3 25657 7200 0.17 0 0
SmallA4 32048 7200 2.85 0 0
SmallA5 19932 7200 0.02 0 0
SmallB1 36444 7200 5.77 0 0
SmallB2 41232 7200 3.28 0 0
SmallB3 47097 7200 5.40 0 0
SmallB4 44067 7200 2.57 0 0
SmallB5 36086 7200 5.76 0 0
SmallC1 55573 7200 3.06 11 10
SmallC2 72174 7200 4.76 12 11
SmallC3 81883 7200 3.55 5 0
SmallC4 74098 7200 8.77 0 0
SmallC5 63387 7200 3.69 7 7
LargeA1 35127 7200 5.66 0 0
LargeA2 44353 7200 11.98 0 0
LargeA3 29663 7200 2.54 0 0
LargeA4 43084 7200 5.27 0 0
LargeA5 43224 7200 5.00 0 0
LargeB1 83596 7200 11.48 0 0
LargeB2 95004 7200 10.22 0 0
LargeB3 84891 7200 -0.02 2 0
LargeB4 72837 7200 10.13 0 0
LargeB5 94950 7200 9.00 0 0
LargeC1 133251 7200 9.78 3 1
LargeC2 136996 7200 54.54 9 3
LargeC3 163414 7200 +∞ 424 0
LargeC4 136600 7200 11.21 19 0
LargeC5 140435 7200 8.04 12 2
Table 2. Cplex performances for group LargeC with time limit of 5 hours.
Instance ID CPU time O ptimGap N otAssSol NotAssP rov
LargeC1 18000 9.78 3 1
LargeC2 18000 54.54 9 3
LargeC3 18000 6.00 6 0
LargeC4 18000 6.87 2 0
LargeC5 18000 8.04 12 2
group SmallA to group SmallC (where in 4 over 5 instances some boxes are not assigned
in the solution). The instances of the large scenario appear more difficult; in the groups
LargeA and LargeB all boxes are assigned, except for instance LargeB3 (in this instance
the negative gap, that should be impossible by definition of the lower bound, must
be considered as a proof of one more box impossible to serve, then it loses its usual

meaning).Finally, the results for the instances of group LargeC are not very satisfactory.
We also solved the instances of group LargeC by imposing a time limit for Cplex of 5
hours (as shown in Table 2). For some instances we obtained a significant improvement,
whereas for some other instances we found the same results produced after 2 hours of
computation.
The groups of instances which can be considered more representative of a real case
are groups LargeB and LargeC. They correspond to a network with 10 terminals and 34
links and to an average request of moving 250 and 420 boxes, respectively. These data
can be considered quite realistic, at least for the first implementations in Italy of this
innovative railway network that now is not yet applied. Moreover, we consider a time
horizon of a week and, again, we think the choice of a weekly planning can make sense
in a real application. These computational results make us think that the proposed plan-
ning procedure could be applied to a real system if the planning is realized off-line one
or two days before the considered horizon. In this case, a much higher time limit (than
5 hours) could be set for the solver, thus probably yielding better solutions. Instead, if
the solutions are needed in a short time and larger instances must be considered, it is
necessary to develop different approaches (i.e. heuristic techniques) for addressing this
planning problem.
5 Conclusions
In this paper we propose a planning procedure in order to meet transportation requests
by using the railway network. The considered railway system is innovative because the
terminals are supposed to be equipped with fast and automatic handling systems, allow-
ing to make containers change different trains on their path from origin to destination.
The solution to this planning problem has been divided in two phases: first the pre-
processing analysis and, second, the optimization (solution of a 0/1 LP problem). To
evaluate the effectiveness of the proposed planning approach we performed some ex-
perimental tests using a set of 30 random generated instances characterized by different
dimensions.
The results obtained from these preliminary tests make us think that the proposed
approach could be applied to a real system, but further extensions and investigations are
needed as well. In fact, since the experimental tests were not completely satisfactory
for the largest instances, some further heuristic techniques (e.g., based on relaxation
or decomposition) are needed to speed-up and simplify the problem solution. These
aspects will be considered in the future development of our research.
References
1. Crainic, T.G., Kim, K.H.: Intermodal transportation. In: Barnhart, C., Laporte, G. (eds.):
Transportation. North Holland (2007)
2. Macharis, C., Bontekoning, Y.M.: Opportunities for OR in intermodal freight transport re-
search: A review. European Journal of Operational Research, 153 (2004) 400–416
3. Wieberneit, N.: Service network design for freight transportation: a review. OR Spectrum, 30
(2008) 77–112

4. Bostel, N., Dejax, P.: Models and algorithms for container allocation problems on trains in a
rapid transshipment shunting yard. Transportation Science, 32 (1998) 370–379
5. Corry, P., Kozan, E.: An assignment model for dynamic load planning of intermodal trains.
Computers and Operations Research, 33 (2006) 1–17
6. Cordeau, J.-F., Toth, P., Vigo, D.: A survey of optimization models for train routing and
scheduling. Transportation Science, 32 (1998) 380-404
7. Newman, A.M., Yano, C.A.: Scheduling direct and indirect trains and containers in an inter-
modal setting. Transportation Science, 34 (2000) 256–270
8. Sacone, S., Siri, S.: A planning approach for freight transportation operations in railway net-
works. Proc. of the IEEE International Conference on Automation and Logistics (2008)