
THE DUAL PHASE EVOLUTION FRAMEWORK FOR
UNDERSTANDING EVOLUTIONARY DYNAMICS IN COMPLEX
ADAPTIVE SYSTEMS
Greg Paperin and Suzanne Sadedin
Clayton School of Information Technology, Monash University, Vic. 3800 Australia
Keywords: Dual phase evolution, Networks, Connectivity, Phase changes, Self-organised criticality, Adaptive cycle.
Abstract: Evidence from several fields suggests that dual phase evolution (DPE) may account for distinctive features
associated with complex adaptive systems. Here, we review empirical and theoretical evidence for DPE in
natural systems and examine the relationship of DPE to self-organized criticality and adaptive cycles. A
general model for DPE in networks is outlined, with preliminary data illustrating the emergence of phase
changes.
1 INTRODUCTION
Complex adaptive and evolutionary systems exhibit
a number of interesting properties such as far-from-
equilibrium dynamics, perpetual novelty and
sustained diversity. While many advances have been
made in understanding specific complex adaptive
systems (CAS), a unifying theory of their underlying
mechanisms remains elusive. Several conceptual
frameworks have been proposed to describe the
properties of CAS. These include the concepts of
self-organised criticality (SOC) (Bak, 1999; Bak et
al., 1988) and the adaptive cycle (Gunderson and
Holling, 2002). While these frameworks effectively
capture some of the observable dynamics seen in
CAS, other properties remain neglected and the
causal processes have not been clearly defined.
Previous research has shown that CAS can be
described in terms of networks of interacting
components (Green, 1993) and that structural
properties of these underlying networks may be used
to explain many of the processes observed in CAS.
Based on this realisation, the notion of Dual Phase
Evolution (DPE) was proposed (Green et al., 2006;
Green et al., 2000). In short, DPE explains CAS
properties such as perpetual novelty and diversity,
modularity, and complexity on all scales in terms of
recurring phase transitions in connectivity and
interaction patterns of underlying networks. DPE
processes can be observed across a wide range of
CAS of various orders of magnitude: from species
evolution and ecosystem development, to socio-
economic systems, to artificial adaptive and
optimisation systems.
In this paper we review some of the empirical
evidence for DPE and contrast it with other
frameworks for understanding CAS dynamics, in
particular SOC and the adaptive cycle. We highlight
the key differences between these frameworks and
DPE and discuss how some processes may be
explained in terms of these different frameworks.
This presents a step towards providing a holistic
understanding of CAS dynamics based on the
underlying network properties. To support our
arguments we outline a simulation model of energy
flow through a network of interacting components.
A number of real world CAS can be mapped to this
network model. While a thorough analysis of the
model dynamics is on-going, the results indicate that
DPE processes emerge in the model under a wide
range of parameters.
2 DUAL PHASE EVOLUTION
2.1 Examples
Evidence from several fields suggests that phase
changes in landscape connectivity form a powerful
agent of evolutionary change and innovation.
Disasters often mediate long-term changes in the
composition of ecological communities, with
135
Paperin G. and Sadedin S. (2009).
THE DUAL PHASE EVOLUTION FRAMEWORK FOR UNDERSTANDING EVOLUTIONARY DYNAMICS IN COMPLEX ADAPTIVE SYSTEMS.
In Proceedings of the International Joint Conference on Computational Intelligence, pages 135-143
DOI: 10.5220/0002320601350143
Copyright
c
SciTePress

established species forming an impenetrable barrier
to invasion by novel species until massive
population destruction clears the landscape.
Palynological data show that changes in species
composition in North American forests are
consistently associated with major wildfires (Green,
1982). At larger geological timescales, many recent
adaptive radiation events are associated with
transitions between glacial and interglacial periods
that lead to drastic changes in habitat connectivity
for a wide variety of species (Willis et al., 2004).
Climate-change mediated variations in sea level can
cause populations living at specific depths to
become fragmented or connected, while temperature
and rainfall variation alters the connectivity of lakes
and waterways and their ecological communities
(Roshier et al., 2001). For example, diverse new
species of cichlids emerged in African rift lakes after
the last Ice Age isolated local fish populations.
Genetic suture zones (areas where locally
differentiated populations meet) in many European
and North American species including trees, insects,
birds and mammals can be traced to population
expansion from refugia that were isolated during
glacial periods (Swenson and Howard, 2005; Hewitt,
2004). Repeatedly-isolated refugia are associated
with speciation events; for example, a meta-analysis
of mitochondrial DNA studies in 63 bird species,
showed that many adaptive radiations initiated in the
Pliocene were completed when glaciers fragmented
populations in the Pleistocene (Avise and Walker,
1998). On the mountainous island of Sulawesi,
adjacent-living similar species of grasshoppers,
macaques, pond-skaters, cicadas, bees, butterflies
and beetles are thought to have arisen during periods
of habitat fragmentation caused by climate change
(Butlin et al., 1998).
At even larger scales, state transitions may be
seen in evolutionary dynamics after environmental
change. Eldredge and Gould (1972) documented
evidence for punctuated equilibria in the fossil
record, arguing that biological history is dominated
by long periods of stasis with occasional bursts of
innovation after mass extinction. These bursts of
innovation, according to Gould (2002), are triggered
by the removal of ecological specialists, opening up
niches for exploitation by the widespread generalists
which preferentially survive mass extinction. These
generalists then undergo adaptive radiation. In this
sense, evolution alternates between long, slow
periods of general stability dominated by species
selection (stability phase) and brief periods of rapid
microevolution where novel adaptations arise
(variation phase). There are several possible
explanations for punctuated equilibrium (Gould and
Eldredge, 2000). However, the strong geological
association between disasters (such as asteroid
strikes, vulcanism and climate change), mass
extinction and subsequent radiation events suggest
that these external drivers are crucial in that they
force the switch from stability to variation phases by
altering the connectivity of food webs and
landscapes.
Simulation experiments confirm this argument.
For instance, Paperin et al. present a model (2007) in
which organisms normally exist within a connected
landscape in which selection maintains them in a
stable state. Intermittent disturbances (such as fires,
commentary impacts) flip the system into a
disconnected phase, in which populations become
fragmented, freeing up areas of empty space in
which selection pressure lessens and genetic
variation predominates. The simulation results show
that DPE-like connectivity phase changes can
facilitate the appearance of complex diversity in a
landscape ecosystem.
Dual phase processes also occur in non-living
natural complex systems. For instance, Perkins
(Perkins, 2003) describes in an overview article how
various kinds of landscape patterns may have been
formed by repeated phase changes in several
interacting geomorphic processes. A well studied
example of such landscapes – the geometric shapes
of stones occurring in many polar and high alpine
environments – has been investigated by Kesser and
Werner (2003) who demonstrated that such patterns
may emerge through freeze-thaw cycles that drive an
interaction between two feedback processes. In the
first process, ice forms in freezing soil, segregating
stones and soil by shifting soil toward soil-rich areas
and stones toward stone-rich areas. In the second
process, stones are transported along the borders of
stone-rich domains, which are squeezed and shaped
under the pressure of expanding freezing soil. The
authors provide a numerical simulation model
(Kessler and Werner, 2003) that can reproduce the
patterns found in natural landscapes of this kind
(Perkins, 2003).
Connectivity phase changes are also the driving
force in many artificial CAS. Phase transitions of
interaction networks have been implicitly present in
many traditional optimisation algorithms in the form
of mediation between local and global search. For
instance, in simulated annealing (Kirkpatrick et al.,
1983; Cerný, 1985) the temperature schedule is used
to arbitrate between local and global search steps.
Similar ideas have been employed to improve
performance in a variety of optimisation techniques
IJCCI 2009 - International Joint Conference on Computational Intelligence
136

that are prone to being caught in undesirable local
optima when applied to non-smooth search spaces.
This includes, for instance, the back propagation
learning algorithm for artificial neural networks.
(e.g. Ramamoorthy and Shekhar, 1989), the Particle
Swarm Optimisation algorithm (e.g. Wang and Li,
2004; Liua et al., 2005), Genetic Programming (e.g.
Cordon et al., 2002) and Support Vector Machines
(e.g. Lin et al., 2008; Sun and Sun, 2005). In the
above algorithms the connectivity of the
transportation network along which the search
proceeds is changed from well connected (global
search, exploration) to poorly connected or
disconnected (local search, exploitation).
In these artificial optimisation systems, phase
transitions occur only once or a few times in one
direction. However, natural DPE processes are
typified by repeated connectivity phase transitions in
both directions. Arguably, optimisation algorithms
supplemented with simulated annealing style
techniques may be improved by incorporating
repeated connectivity phase transitions in both
directions. An instance of this approach is a
modification of the Cellular Genetic Algorithm
(Alba and Dorronsoro, 2008; Whitley, 1993). Kirley
et al. (2002; 1998) modified this algorithm to
supplement it with insights from population
dynamics and landscape ecology. The evolving
population was placed in a 2-dimensional cellular
automation grid that is subjected to intermittent
“disasters” that eliminate all solutions in one part of
the grid. As a result, the population becomes
fragmented and the gene flow between the sub-
populations is diminished or interrupted. This allows
the sub-populations to diverge and slows down
convergence. Recombination of diverged sub-
populations while re-populating areas freed by
disasters often leads to discovery of new and fitter
solutions. The Cellular Genetic Algorithm modified
in this way outperforms the standard Cellular
Genetic Algorithm on a number of hard test
problems (Kirley, 2002; Kirley et al., 1998).
It should be noted that in this case, the DPE
phase transition occurs repeatedly in both directions.
Two important interaction networks can be
identified within the cellular grid. Firstly, there is the
connectivity network between the populated grid
cells. The connectivity of this network plays a role
in determining the amount of gene (information)
flow between different cells. Thus, connectivity in
this network influences whether the population
evolves as a whole or as divergent sub-populations.
The second network is the connectivity network of
free grid cells. These cells can be populated by
newcomers without substantial competition. During
phases where this network is well connected the
algorithm has the opportunity to experiment with
candidate solutions that may be less fit than some
other part of the grid population, but that have
potential to evolve towards a different, possibly
better local optimum.
2.2 The DPE Framework
A common thread in all of the above examples is
that complex properties of systems are mediated by
qualitative changes in the connectivity structure of
the underlying networks. The connectivity structure
can be classified into two main states or phases:
“connected” and “disconnected”. The “connected”
phase is typified by high edge density and short
paths lengths. In this phase interactions can therefore
occur between most of the network components. In
the “disconnected” phase edge density is low, paths
lengths are long, and the network typically consists
of several disconnected components. Interactions in
the disconnected phase typically occur locally or
only within strongly connected components.
Since networks are inherent in the structure and
behaviour of all complex systems (Green, 1993), a
connectivity avalanche (Erdös and Rényi, 1960)
underlies many kinds of critical phase changes
(Green, 2000). Therefore all such systems can
switch between the two above phases. Systems in
the disconnected phase tend to be balanced. They
may exhibit strong local variability, but typically
little large-scale variation. Global responses to
external stimuli are constrained, as perturbations
cannot propagate far. Systems in the connected
phase, in contrast, exhibit less local variability, but
significant variation on all scales in the sense that
responses to external stimuli are generally hard to
predict. The rich connectivity allows perturbations to
propagate far, affecting many system parts (Paperin
et al., 2007).
DPE occurs when an evolving system repeatedly
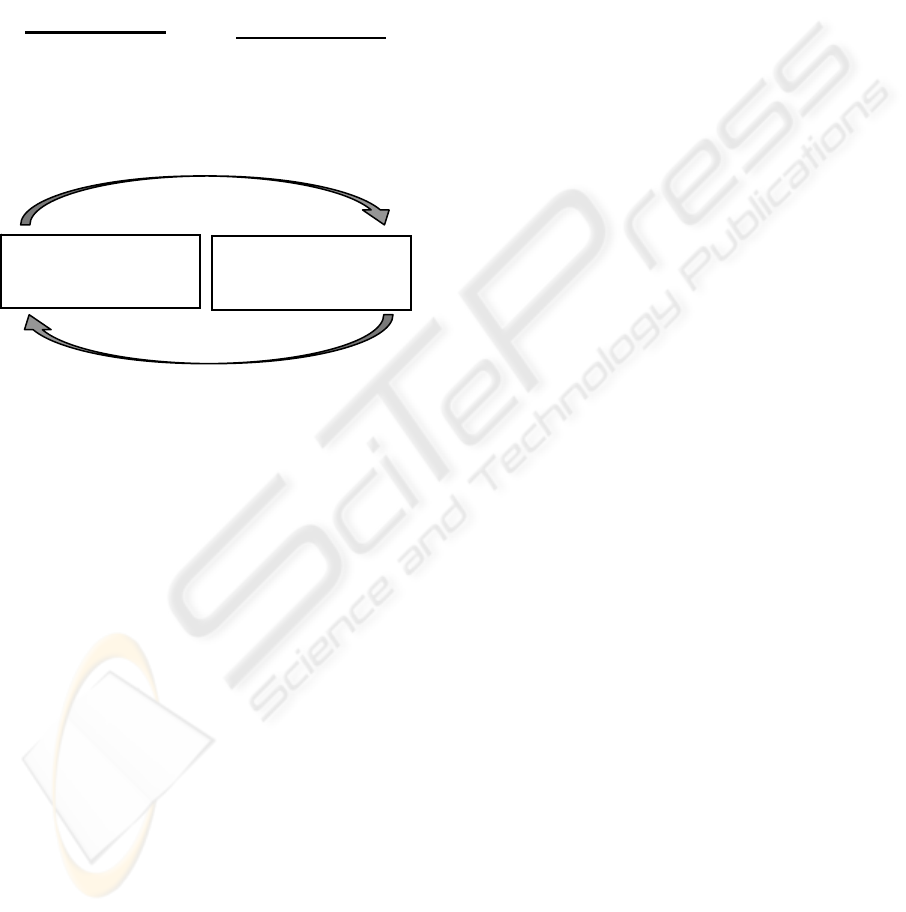
switches between these two phases (figure 1).
Crucial for understanding many DPE systems is the
mechanism responsible for these repeated phase
transitions. There is much evidence that CAS
generally self-organise towards a stable, balanced
state. Stabilising forces include lower order
dynamics, such as feedback loops, and higher order
dynamics, such as selection (in a general sense)
(Lenton and Van Oijen, 2002). Analytical (Watson
and Lovelock, 1983; Weber, 2001) and
computational (Lenton and Van Oijen, 2002) models
show that lower-order local dynamics can stabilise
THE DUAL PHASE EVOLUTION FRAMEWORK FOR UNDERSTANDING EVOLUTIONARY DYNAMICS IN
COMPLEX ADAPTIVE SYSTEMS
137
systems over a large range of external forcing, and
that higher order local dynamics (evolutionary
dynamics) can greatly increase the stabilising effect.
The adaptive forces that underlie global stability of
CAS also inhibit novelty and change. In particular,
selection acting on system components at various
scales, as well as on topology and interactions, may
drive a system as a whole to a local optimum state,
halting innovation (Holland, 1995). Two
mechanisms work against such long-term stasis.
Figure 1: The mechanism of Dual Phase Evolution.
Systems flip between loosely connected balance and well
connected variation phases. Perturbations and external
stimuli unbalance stable systems, variation facilitates
evolutionary exploration, and internal pressures drive the
system into a new stable state.
One mechanism is co-evolution. Local
adaptation of system components by selection may
affect the selection criteria for other components,
which will adapt as a result. This in turn affects the
fitness landscapes of the components that initiated
the changes. Such feedback loops may form sources
of perpetual novelty. However, it is not clear that co-
evolution fully accounts for the innovation observed
in many natural CAS. For instance, analytical
models (Gavrilets, 2004) suggest that selection, not
variation, drives speciation. Co-evolutionary
feedback loops are likely to rapidly lead to stable
system states. Once such a local optimum is reached,
selection makes successful variations highly unlikely
(Gavrilets, 2004).
A second mechanism that may underlie continual
novelty in CAS is disturbance. As discussed in
section 2.1, evolutionary innovations often coincide
with external perturbations. External disturbances
may affect both system components and interaction
networks, thus moving systems away from local
optima. Densely connected interaction networks,
while providing many stabilising interactions, also
facilitate disturbance propagation. The complexity
of dense interaction networks makes large-scale
responses to disturbances essentially unpredictable.
Once away from a local optimum, systems enter
a variation phase. Chance variation of local
components may provide better adaptation to local
constraints; selection facilitates proliferation of such
changes within networks. Selection then amplifies
variations and eliminates destabilising interactions,
reducing connectivity, and components and their
interactions self-organise towards new local optima.
Over time, surviving system components develop
new interactions, increasing the connectivity of
interaction networks that survived previous
disturbances. Eventually, the system enters a new
balance phase.
While some parts of a system may be completely
or partly reorganised during a variation phase
following a particular disturbance, others remain
stable. These stable parts may form new interactions
and assume new roles, acting as functional
components during a variation phase. A simulation
by Paperin et al. (Paperin et al., 2008) demonstrated
that DPE can result in modular networks. We
conjecture that this mechanism may also contribute
to emergence of hierarchical organisation in CAS.
2.3 DPE and Self-organised Criticality
DPE can be linked to several other key concepts in
CAS theory. One such concept is Self-Organised
Criticality (SOC) (Bak, 1999; Bak et al., 1988).
Under SOC, CAS self-organise to a critical state
where system behaviour emerges from propagation
of stimuli via local component interactions. SOC
suggests that CAS evolve towards the “edge-of-
chaos” (Langton 1990; Langton 1991), a transition
state between the stasis of equilibrium systems and
the unpredictability of chaotic systems.
Sizes of stimuli propagation avalanches in SOC
systems follow a power distribution, leading some
researchers to argue that power-distributed data
imply SOC. Models (Bak, 1999) suggest ways in
which certain natural systems may exhibit SOC
dynamics. However, the general applicability of
SOC remains doubtful. Other processes also lead to
power-law distributed data. For example, it has been
proposed (Bak and Sneppen, 1993) that the
biosphere self-organises to a critical state,
potentially explaining punctuated equilibria
(Eldredge and Gould, 1972). However, (Newman,
1997) demonstrates a non-critical extinction model
that yields a power-law with an exponent closer
Balance Phase
- Loosely connected
components
- Selection and other stabilising
forces dominate
- Local variability
- Little global variation
Variation Phase
- Richly connected components
- Little local variability
- Response to stimuli
unpredictable
- Global variation
perturbation
Unbalanced system
- high connectivity
- global interactions
- modifies network components
- destroys connectivity patterns
- affects relationships
Stable system
- low connectivity
- local interactions
pressure towards stability
- e.g. selection
IJCCI 2009 - International Joint Conference on Computational Intelligence
138
(Lenton and Van Oijen, 2002) to the empirical
punctuated equilibria data. SOC also appears to
require fine-tuning of an order parameter (de
Carvalho and Prado, 2000; Sornette et al., 1995),
and the applicability of SOC to non-conservative
systems (de Carvalho and Prado, 2000; Kinouchi
and Prado, 1999) remains unclear.
To describe DPE using the SOC-vocabulary:
CAS develop to a balance-state, where they are
stabilised by internal forces (e.g. selection, negative
feedback mechanisms). External disturbances
repeatedly push a system across the critical region,
to a chaotic state (in the sense that systems responses
to stimuli are unpredictable), from which the system
returns to a new balance-state, accumulating order
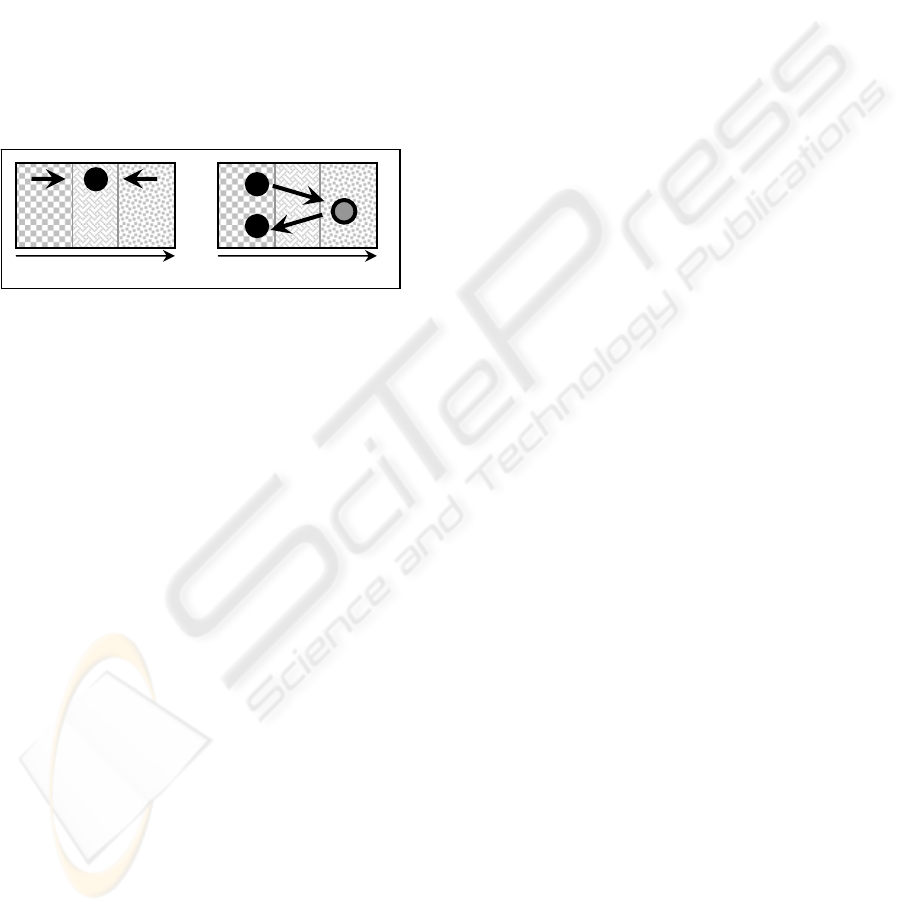
and complexity on the way (figure 2).
Figure 2: Dual Phase Evolution vs. Self-Organised
Criticality. SOC-theory suggests that CAS self-organise to
a transition state between the general stasis of equilibrium
systems and the random behaviour of chaotic systems
(left). According to DPE, CAS are repeatedly pushed from
a balance-phase to a variation-phase by external
disturbances (right). The X-axis on this metaphoric
illustration represents the degree of predictability of
system’s responses to stimuli.
Often, SOC is used to express that a system has
self-organised to a specific state, without describing
the underlying processes. The DPE framework
attempts to define the internal forces responsible for
system states. In this sense some systems may self-
organise to a critical state through DPE. For
instance, scale-free networks (Albert and Barabási,
2000) are traditionally associated with SOC because
their node degrees follow a power distribution.
Traditionally, scale-free topologies were thought to
arise through preferential node attachment during
network growth (Albert and Barabási, 2000).
However, scale-free topologies can arise through
DPE in networks of constant size (Paperin et al.,
2008). Networks developed this way may underlie
some systems with apparent SOC dynamics.
2.4 DPE and the Adaptive Cycle
An influential concept in CAS theory is the adaptive
cycle (AC) (see Gunderson and Holling (2002)). The
AC extends the idea of ecological succession
(Gleason, 1927), and is predominantly applied to
ecological and socio-ecological systems, especially
with reference to ecosystem management and
resilience. The AC identifies 4 phases in ecological
succession:
▪ a growth and exploitation phase (designated r), in
which new or freed-up areas and niches are
rapidly populated by opportunistic organisms;
▪ a conservation phase (K) signified by
competition, selection and resource accumulation;
▪ a collapse or release phase (Ω), in which
accumulated resources are catastrophically
released, often mediated by disturbances;
▪ a reorganisation phase (α) in which the remains
of an Ω-collapse are reorganised and restructured.
The AC concept attributes typical CAS
properties to each phase. Resilience against external
forcing is expected to be high during r and α phases
but low during K, while resource availability is high
during α and K phases, but low during r and Ω.
Connectedness of control variables is maximal near
the end of a K-phase. The AC provides a descriptive
formalism for self-organisation in ecosystems. DPE
theory distils concepts of the AC that are applicable
to a wider range of CAS and provides a causal
model based in network theory.
The balance phase in DPE loosely corresponds to
the r-K transition in AC. This phase is signified by
stabilising selection, increasing connectivity, and
growing potential for disturbance propagation. The
variation phase in DPE loosely corresponds to the
Ω-α-r transition in AC. This is a phase of innovation
and re-organisation of underlying networks.
Notably, connectedness in AC refers to the
richness of interactions of control variables. In fact,
there may be several interaction networks with
different connectivity regimes within a system at any
one time. For example, species in food webs and
populations in landscapes form interaction networks
that act simultaneously on the same groups but may
have very different topologies. The structural
properties of the interaction network of control
variables may thus be different from the interaction
network of components where disturbances
propagate; a comprehensive CAS theory must
account for this fact.
3 A DPE SIMULATION MODEL
To further investigate the DPE process and the role
of disturbances and connectivity in CAS we created
predictability chaos
the edge
of chaos
predictability chaos
disturbance
stabilisation
THE DUAL PHASE EVOLUTION FRAMEWORK FOR UNDERSTANDING EVOLUTIONARY DYNAMICS IN
COMPLEX ADAPTIVE SYSTEMS
139

an abstract model of resource flow through a
network. We briefly discuss the model and some
preliminary results here. The main objective of this
paper is to review the empirical evidence for DPE
and to discuss its relationship to other CAS theories.
The space limit does not permit us to examine the
model in greater detail and more detailed results will
be published elsewhere (paper in preparation).
The model consists of a number of nodes
connected via directed edges. Energy flows along
edges and nodes require energy to sustain
themselves. All nodes in the system are designated
“component nodes”, except for one, designated the
“source”. The source node does not require energy,
instead it produces a constant amount of energy at
each iteration. Energy flows along downstream
connections attached to a node. Each model iteration
consists of three stages: energy propagation, node
maintenance and structural modification.
Energy Propagation. At the start of each iteration
each component node c passes a proportion of its
stored energy f
c
along its downstream connections.
Total energy propagated downstream by c is d
c
= f
c
× (1 - r
c
), where the retention factor
0 ≤ r
c
< 0 is a random number drawn when c is
created. The remaining energy (f
c
– d
c
) is retained
by the node. If c has no outgoing links, all of f
c
is
retained. Nodes at the end of downstream edges of c
compete for the energy propagated by c.
Competition for resources in real systems requires
energy. This is modelled by a competition cost
factor k
c
= 1 / (1 + e
2 × (
l
c
-
i
c
)
), where l
c
is the
number of downstream edges from c, and i
c
> 0 is a
random number drawn when c is created, it is the
maximum value of l
c
such that most energy is not
wasted by competition expenses. Each of the l
c
downstream edges receives an equal amount of
(d
c
× k
c
/ l
c
) units of energy from c. Any energy
conversion in nature comes with a loss. To model
this, every edge g has a flow efficiency value w
g
associated with it, such that the amount of energy
actually arriving at node c
q
from node c
p
is
u
q,p
= (d
c
× k
c
/ l
c
) – w
g
(
p,q
)
, where g(p, q) is the
edge from c
p
to c
q
and w
g
(
p,q
)
is a random number
drawn when g is created.
Node Maintenance. After all nodes have
propagated energy downstream, the total available
energy f
c
at each component node c is equal to the
amount of energy retained by c during the
propagation stage plus the sum of the incoming
energy from all upstream edges. Every c has an
associated maintenance cost m
c
> 0 selected
randomly when c is created. To maintain its
existence, every c expends m
c
energy units per
iteration. If m
c
> f
c
, then c dies and is removed from
the system along with all connected up- and down-
stream edges. The source node never dies. If c
accumulates a large amount of energy, it reproduces.
This happens by creating a duplicate copy h of c.
The offspring h receives the same number of edges
as c. Each of these edges may be connected either to
the respective partner of c, or to any other random
node with equal probability, thus modelling random
mutation. The reproduction process consumes an
amount of energy significantly larger than m
c
and
remaining energy is divided evenly between c and h.
Structural Modification. Every iteration, a new
component or a new edge is introduced into the
network with a small probability. When a new
component c
n
is introduced, for every existing node
p, an edge g(p, n) is added with a small probability.
New edges connect two randomly selected existing
nodes. Similarly, nodes and edges are removed from
the network with a small probability at each iteration
simulating external disturbances.
The presented model captures major features of
resource flow dynamics in several real-world CAS.
For instance, the energy flow through food webs in
ecosystems follows patterns very similar to those
described here. Resource flow between primary and
intermediate producers, and end-consumers in
economies follows a similar pattern. Thus, the
results obtained form our abstract model allow
conclusions about a variety of CAS.
3.1 Results
Model dynamics explored under a range of
parameter values coincide with the behaviour
expected under the DPE framework. A detailed
discussion is beyond the scope of this paper, but we
briefly overview some of the results here. Some
indicators of network dynamics are the number C of
component nodes, the total amount E of energy
stored by all component nodes in the system, and the
network edge density D. The maximum node age A
is an indicator on internal stability of the system.
In the absence of external disturbances
(probability of random node and edge removal is
zero), C and E are lower on average compared to
cases with disturbances. This initially surprising
result can be explained by the DPE process. In the
absence of disturbances unfavourable configurations
can only be removed through node starvation. In the
presence of disasters that propagate through the
IJCCI 2009 - International Joint Conference on Computational Intelligence
140
system by cutting off nodes and reducing
connectivity, the remaining network sub-structures
exhibit more efficient and robust connectivity
patterns. Additionally, newly created nodes can
better compete with established nodes that stored
significant amounts of energy when all nodes can
equally be affected by disturbances. This increases
potential for innovation and for discovery of even
more stable configurations.
Another consistently emerging pattern is that low
values of D strongly correlate with high values of C
and E: a small number of connections is enough to
efficiently distribute the energy across the
components and additional edges lead to excessive
energy expenditure due to unnecessary competition
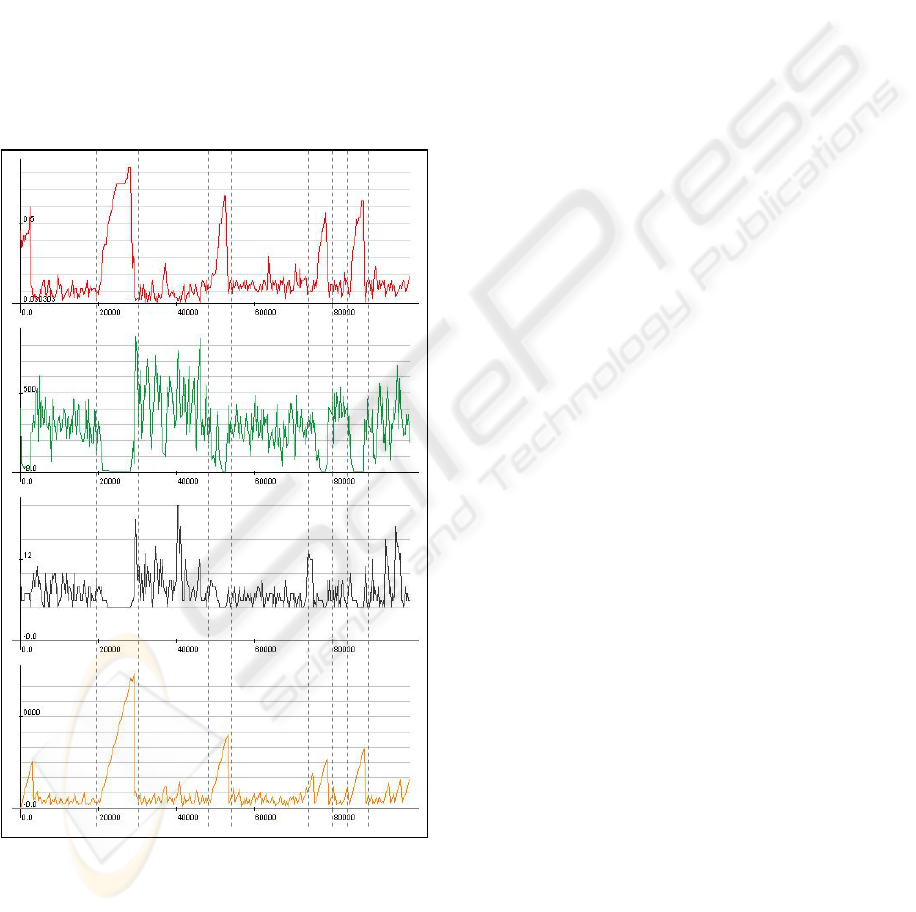
and flow friction along the edges (figure 3).
Figure 3: A typical simulation run. Shown are (from top to
bottom): edge density D, total stored energy E, number of
component nodes C, oldest node age A. Mean node age
(not shown) strongly correlates with A. The x-axes
represent iterations. The vertical dashed lines are a visual
aid to stress apparent phase changes.
In a typical run A is normally low (< 1000),
indicating internal instability. Over time, robust
network configurations are discovered, signified by
a growing value of A (>> 1000). Edge density in
these stable configurations grows, making them less
efficient and more susceptible to catastrophic change
caused by structural modifications. Eventually, E
reaches a very low value and the stable
configurations collapse leading to the next variation
phase (figure 3). This behaviour is in line with the
predictions of DPE. However, in most of our
experiments the variation phase was significantly
longer than the DPE framework predicts. This
observation may be explained by the absence of
higher order stabilising control mechanisms such as
selection between network configurations. Further
experiments will test this conjecture.
4 CONCLUSIONS
Previous work shows that complex adaptive and
evolutionary systems can be represented as networks
of interacting components and that many interesting
properties of CAS may be explained in terms of a
network theoretical framework termed Dual Phase
Evolution. According to DPE, networks underlying
complex systems adapt and self-organise by
alternately switching between two phases: a phase of
high connectivity dominated by global component
interactions and a phase of low connectivity
dominated by local interactions.
Here we demonstrated that DPE may provide a
causal explanation for known CAS properties
typically expressed through other established
descriptive formalisms. Simulation results indicate
that DPE-like phase changes arise in an abstract
model of resource flow in a network that is
representative of a variety of systems. This work
provides a step towards an integral understanding of
CAS and suggests that more advances can be made
by further empirical and theoretical studies of Dual
Phase Evolution.
REFERENCES
Alba, E. & Dorronsoro, B. (2008) Cellular Genetic
Algorithms, Springer.
Albert, R. & Barabási, A. L. (2000) Topology of Evolving
Networks: Local Events and Universality. Physical
Review Letters, 85, 5234-5237.
Avise, J. & Walker, D. (1998) Pleistocene
phylogeographic effects on avian populations and the
THE DUAL PHASE EVOLUTION FRAMEWORK FOR UNDERSTANDING EVOLUTIONARY DYNAMICS IN
COMPLEX ADAPTIVE SYSTEMS
141

speciation process. Proceedings of the Royal Society
B: Biological Sciences, 265, 457-463.
Bak, P. (1999) How Nature Works: The Science of Self-
Organized Criticality, Springer-Verlag Telos; Reprint
edition.
Bak, P. & Sneppen, K. (1993) Punctuated equilibrium and
criticality in a simple model of evolution. Physical
Review Letters, 71, 4083.
Bak, P., Tang, C. & Weisenfeld, K. (1988) Self-Organized
Criticality. Physical Review A, 38, 364-374.
Butlin, R., Walton, C., Monk, K. & Bridle, J. (1998)
Biogeography of Sulawesi grasshoppers, genus
Chitaura, using DNA sequence data. Biogeography
and geological evolution of Southeast Asia. Backhuys
Publishers, Leiden, The Netherlands, 355–359.
Cerný, V. (1985) Thermodynamical approach to the
traveling salesman problem: An efficient simulation
algorithm. Journal of Optimization Theory and
Applications, 45, 41-51.
Cordon, O., Moya, F. & Zarco, C. (2002) A new
evolutionary algorithm combining simulated annealing
and genetic programming for relevance feedback in
fuzzy information retrieval systems. Soft Computing,
6, 308-319.
De Carvalho, J. X. & Prado, C. P. C. (2000) Self-
Organized Criticality in the Olami-Feder-Christensen
Model. Physical Review Letters, 84, 4006.
Eldredge, N. & Gould, S. J. (1972) Punctuated Equilibria:
An Alternative to Phyletic Gradualism, San Francisco,
Freeman Cooper.
Erdös, P. & Rényi, A. (1960) On the Evolution of Random
Graphs Magyar Tudományos Akadémia. Matematikai
Kutató Intézetének Közleményei, 5, 17-61.
Gavrilets, S. (2004) Fitness Landscapes and the Origin of
Species, Princeton / Oxford, Princeton University
Press.
Gleason, H. A. (1927) Further views on the succession-
concept. Ecology, 8, 299-326.
Gould, S. (2002) The structure of evolutionary theory,
Belknap Press.
Gould, S. & Eldredge, N. (2000) Punctuated equilibrium
comes of age. Shaking the Tree: Readings from Nature
in the History of Life, 17.
Green, D. (1982) Fire and stability in the postglacial
forests of southwest Nova Scotia. Journal of
Biogeography, 29-40.
Green, D. G. (1993) Emergent Behaviour in Biological
Systems. In Green, D. G. & Bossomaier, T. R. J.
(Eds.) Complex Systems: From Biology to
Computation. IOS Press.
Green, D. G. (2000) Self-Organization in complex
systems. In Bossomaier, T. R. J. & Green, D. G. (Eds.)
Complex Systems. Cambridge University Press.
Green, D. G., Leishman, T. G. & Sadedin, S. (2006) Dual
Phase Evolution: a mechanism for self-organization in
complex systems. International Journal Complex
Systems.
Green, D. G., Newth, D. & Kirley, M. G. (2000)
Connectivity and catastrophe - towards a general
theory of evolution. In Bedau, M., Mccaskill, J. S.,
Packard, N. H., RASMUSSEN, S., Mccaskill, J. &
Packard, N. (Eds.) Artificial Life VII.
Gunderson, L. H. & Holling, C. S. (2002) Panarchy:
understanding transformations in human and natural
systems, Island Press.
Hewitt, G. (2004) Genetic consequences of climatic
oscillations in the Quaternary. Philosophical
Transactions of the Royal Society of London. Series B,
Biological Sciences, 359, 183-195.
Holland, J. H. (1995) Hidden Order: How Adaptation
Builds Complexity, Perseus Books.
Kessler, M. A. & Werner, B. T. (2003) Self-organization
of sorted patterned ground. Science, 299, 380-383.
Kinouchi, O. & Prado, C. P. C. (1999) Robustness of scale
invariance in models with self-organized criticality.
Physical Review E, 59, 4964.
Kirkpatrick, S., Gelatt, C. D. & Vecchi, M. P. (1983)
Optimization by simulated annealing. Science, 220,
671-680.
Kirley, M. G. (2002) A Cellular Genetic Algorithm with
Disturbances: Optimisation Using Dynamic Spatial
Interactions. Journal of Heuristics, 8, 321-242.
Kirley, M. G., LI, X. & Green, D. G. (1998) Investigation
of a cellular genetic algorithm that mimics landscape
ecology. IN AL., M. E. (Ed.) Simulated Evolution and
Learning (SEAL'98). Springer.
Langton , C. G. (1990) Computation at the edge of chaos:
Phase transitions and emergent computation. Physica
D: Nonlinear Phenomena, 42, 13-37.
Langton , C. G. (1991) Life at the Edge of Chaos.
Artificial Life II. Addison-Wesley.
Lenton, T. M. & Van Oijen, M. (2002) Gaia as a Complex
Adaptive System. Philosophical Transactions of the
Royal Society: Biological Sciences, 357, 683-695.
Lin, S. W., Lee, Z. J., Chen, S. C. & Tseng, T. Y. (2008)
Parameter determination of support vector machine
and feature selection using simulated annealing
approach. Applied Soft Computing Journal, 8, 1505-
1512.
Liua, B., Wanga, L., Jina, Y.-H., Tangb, F. & Huanga, D.-
X. (2005) Improved particle swarm optimization
combined with chaos. Chaos, Solitons & Fractals, 25,
1261-1271.
Newman, M. E. J. (1997) A model of mass extinction.
Journal of Theoretical Biology, 189, 235-252.
Paperin, G., Green, D. G. & Leishman, T. G. (2008) Dual
Phase Evolution and Self-organisation in Networks.
7th International Conference on Simulated Evolution
and LEarning (SEAL'08). Springer.
Paperin, G., Green, D. G., Sadedin, S. & Leishman, T. G.
(2007) A Dual Phase Evolution model of adaptive
radiation in landscapes. In Randall, M., Abbass, H. A.
& Wiles, J. (Eds.) The Third Australian Conference on
Artificial Life (ACAL'07). Gold Coast, Australia,
Springer.
Perkins, S. (2003) Patterns from nowhere: Natural forces
bring order to untouched ground. Science news, 163,
314-316.
Ramamoorthy, C. V. & Shekhar, S. (1989) Stochastic
backpropagation: a learning algorithm for
generalisation problems. 13th Annual International
IJCCI 2009 - International Joint Conference on Computational Intelligence
142

Computer Software and Applications Conference 1989
(COMPSAC'89). Orlando, FL, USA.
Roshier, D., Robertson, A., Kingsford, R. & Green, D.
(2001) Continental-scale interactions with temporary
resources may explain the paradox of large
populations of desert waterbirds in Australia.
Landscape Ecology, 16, 547-556.
Sornette, D., Johansen, A. & Dornic, I. (1995) Mapping
Self-Organized Criticality onto Criticality. Journal de
Physique I, 5, 325-335.
Sun, F. & Sun, M. (2005) Transductive Support Vector
Machines Using Simulated Annealing. In Hao, Y.,
Liu, J., Wang, Y., Cheung, Y.-M., Yin, H., Jiao, L.,
Ma, J. & Jiao, Y.-C. (Eds.) 2005 International
Conference Computational Intelligence and Security
(CIS'2005). Berlin / Heidelberg, Springer.
Swenson, N. & Howard, D. (2005) Clustering of contact
zones, hybrid zones, and phylogeographic breaks in
North America. The American Naturalist, 166, 581-
591.
Wang, X. H. & LI, J. J. (2004) Hybrid particle swarm
optimization with simulated annealing. 2004
International Conference on Machine Learning and
Cybernetics.
Watson, A. J. & Lovelock, J. E. (1983) Biological
homeostasis of the global environment: the parable of
Daisyworld. Tellus B, 35, 284-289.
Weber, S. L. (2001) On Homeostasis in Daisyworld.
Climatic Change, 48, 465-485.
Whitley, L. D. (1993) Cellular Genetic Algorithms. 5th
International Conference on Genetic Algorithms.
Morgan Kaufmann.
Willis, K., Bennett, K. & Walker, D. (2004) The
evolutionary legacy of the Ice Ages–Introduction.
Phil. Trans. R. Soc. Lond. B, 359, 157–158.
THE DUAL PHASE EVOLUTION FRAMEWORK FOR UNDERSTANDING EVOLUTIONARY DYNAMICS IN
COMPLEX ADAPTIVE SYSTEMS
143
