
A TUNABLE REAL-WORLD MULTI-FUNNEL BENCHMARK
PROBLEM FOR EVOLUTIONARY OPTIMIZATION
And Why Parallel Island Models Might Remedy the Failure of CMA-ES on It
Christian L. M¨uller and Ivo F. Sbalzarini
Institute of Theoretical Computer Science and Swiss Institute of Bioinformatics
ETH Zurich, Universit¨atstrasse 6, 8092 Zurich, Switzerland
Keywords:
Benchmark, Multi-funnel landscape, Lennard-Jones cluster, CMA-ES, Parallel island model.
Abstract:
A common shortcoming in the Evolutionary Computation (EC) community is that the publication of many
search heuristics is not accompanied by rigorous benchmarks on a balanced set of test problems. A welcome
effort to promote such testsuites are the IEEE CEC competitions on real-valued black-box optimization. These
competitions prescribe carefully designed synthetic test functions and benchmarking protocols. They do,
however, not contain tunable real-world examples of the important class of multi-funnel functions. We argue
that finding minimum-energy configurations of 38-atom Lennard-Jones (LJ
38
) clusters could serve as such
a benchmark for real-valued, single-objective evolutionary optimization. We thus suggest that this problem
be included in EC studies whenever general-purpose optimizers are proposed. The problem is tunable from
a single-funnel to a double-funnel topology. We show that the winner of the CEC 2005 competition, the
Evolution Strategy with Covariance Matrix Adaptation (CMA-ES), works on the single-funnel version of this
test case, but fails on the double-funnel version. We further argue that this performance loss of CMA-ES
can be relaxed by using parallel island models. We support this hypothesis by simulation results of a parallel
island CMA-ES, the Particle Swarm CMA-ES, on a subset of the multi-funnel functions in the CEC 2005
benchmark.
1 INTRODUCTION
High-dimensional, non-convex, and noisy optimiza-
tion problems are commonplace in physics, engineer-
ing, and biology. The prominent example of protein
structure prediction can, e.g., be considered a mini-
mization problem over an empirical energy landscape.
In many cases, such problemscan only be tackled effi-
ciently by evolutionary optimization methods such as
the Evolution Strategy with Covariance Matrix Adap-
tation (CMA-ES) (Hansen and Ostermeier, 2001), a
particularly successful gradient-free heuristic for real-
valued black-box optimization. During exploration of
the search space, CMA-ES samples a population of
candidate solutions from a multivariate Gaussian dis-
tribution. The mean and the covariance matrix of the
sampling distribution are continuously adapted in or-
der to guide the search toward promising regions of
the space.
Assessing the efficacy and efficiency of evolution-
ary algorithms is empirical by nature since theoreti-
cal convergence analyses are missing for most prob-
lems of practical importance. Unfortunately, it is
a common shortcoming in the Evolutionary Com-
putation (EC) community that many publications on
new search heuristics are not accompanied by rig-
orous benchmarks on a diverse and balanced set of
test problems. It is still commonplace that authors
choose an arbitrary set of popular benchmark func-
tions and compare the performance of their algorithm
to that of an arbitrary set of existing heuristics. A
welcome exception is the series of IEEE CEC compe-
titions on real-valued black-box optimization. Start-
ing in 2005 with a contest on single-objective black-
box optimization (Suganthan et al., 2005), these com-
petitions prescribe carefully designed synthetic func-
tion sets and benchmarking protocols. A generally
accepted standard set of real-world benchmark prob-
lems, however, is still not available.
While studies on synthetic test suites allowfair and re-
producible comparison between algorithms, they only
provide limited insight into why a particular heuris-
tic works on certain functions, but fails on others.
In recent years, it has been suggested that the global
248
L. Müeller C. and F. Sbalzar ini I. (2009).
A TUNABLE REAL-WORLD MULTI-FUNNEL BENCHMARK PROBLEM FOR EVOLUTIONARY OPTIMIZATION - And Why Parallel Island Models Might
Remedy the Failure of CMA-ES on It.
In Proceedings of the International Joint Conference on Computational Intelligence, pages 248-253
DOI: 10.5220/0002335202480253
Copyright
c
SciTePress

topology of a problem may have a strong influence
on the performance of search heuristics. (Hansen
and Kern, 2004) and (Sutton et al., 2006), for ex-
ample, suggested that the performance of CMA-ES
and Particle Swarm Optimization (PSO) can strongly
decrease on test functions with a multi-funnel topol-
ogy, where local optima cannot be interpreted as per-
turbations to an underlying convex (unimodal) topol-
ogy. (Lunacek et al., 2008) further examined this is-
sue by considering the search performance of CMA-
ES on synthetic, tunable double-funnel landscapes.
The global structure of these landscapes consists of
a composition of two sphere functions whose sizes
and depths are adjustable. They report two remark-
able observations. First, the probability of finding the
minimum with CMA-ES without restarts decreases
with increasing population size when considering a
double-sphere landscape where the global minimum
lies in the smaller funnel. Second, introduction of
local multi-modality in the double-sphere function
through a Rastrigin function triggers an irresolvable
trade-off for the optimal population size of CMA-
ES: Local multi-modality demands larger populations
while the double-funnel favors the opposite. There-
fore, the probability of finding the global minimum
with CMA-ES on the designed double-Rastrigin func-
tion is low for any population size. Unfortunately,
problemswith a multi-funnel structure are not of mere
academic interest. Prominent real-world examples
include trajectory planning in space missions, pro-
tein aggregation and misfolding (Clark, 2004), and
the potential-energy surfaces (PES) of atomic clusters
(Wales, 2004).
The purpose of the present paper is twofold. First, we
propose a tunable real-world benchmark problem for
real-valued, single-objective, gradient-free evolution-
ary optimization: the prediction of minimum-energy
configurations of the 38-atom Lennard-Jones (LJ
38
)
cluster. This problem has been intensively studied
in physical chemistry, and we expect this to be valu-
able to the EC community. The LJ
38
problem exhibits
a double-funnel PES topology (Doye et al., 1999),
which can be transformed to a single-funnel topology
by adding a compression penalty. This transforma-
tion is tunable by a single, scalar parameter. We show
that the LJ
38
cluster problem cannot be solved by the
winner of IEEE CEC 2005 contest, a restart variant of
CMA-ES with iteratively increasing population size
(IPOP-CMA-ES) (Auger and Hansen, 2005), unless
the compression penalty is included. We therefore
propose that the LJ
38
problem should be included in
future EC studies whenever a novel general-purpose
optimizer is introduced.
Second, we propose that the use of parallel island
models can remedy the decreased performance of
IPOP-CMA-ES on multi-funnel functions. We be-
lieve that it is beneficial to evolve several commu-
nicating CMA-ES instances on the problem in par-
allel, rather than increasing the population size of a
single CMA-ES instance. We support this hypothesis
by simulation results of a parallel island CMA-ES, the
Particle Swarm CMA-ES (PS-CMA-ES), on a subset
of multi-funnel functions from the IEEE CEC 2005
test suite.
This paper is organized as follows: In Section 2 we
briefly review the IEEE CEC 2005 benchmark test
suite and introduce the real-world multi-funnel en-
ergy landscape of the 38-atom Lennard-Jones clus-
ter. Section 3 reviews (IPOP-)CMA-ES, the concept
of parallel island models, and PS-CMA-ES. In Sec-
tion 4 we present the results of numerical experiments
with IPOP-CMA-ES and PS-CMA-ES. Section 5 dis-
cusses these results and concludes this work.
2 MULTI-FUNNEL
OPTIMIZATION PROBLEMS
Problems with a multi-funnel topology arise in di-
verse scientific areas such as, e.g., trajectory planning
in space missions or protein aggregation and misfold-
ing in biology. Although there is no clear mathemat-
ical definition of the term multi-funnel, we consider a
problem multi-funnel if it has no underlying convex
topology on a global length scale. Probably the best-
known example for a multi-funnel function is Schwe-
fel’s problem. The Rastrigin function, on the other
hand, is highly multi-modal, but not multi-funnel due
to its globally spherical topology. In this section, we
first revisit the synthetic multi-funnel problems of the
IEEE CEC 2005 test suite and then propose the LJ
38
problem as a tunable real-world test case for gradient-
free optimization.
2.1 The IEEE CEC 2005 Test Suite
One key attempt to provide a standard for perfor-
mance evaluation and analysis of real-valued search
heuristics in the EC community is the IEEE CEC
2005 test suite (Suganthan et al., 2005). The bench-
mark suite includes a set of 25 test functions from a
variety of classes such as uni-/multimodal, (non-) sep-
arable, noisy, (a-)symmetric, and scalable. Functions
f11 to f13 and f15 to f25 are multi-funnel. Along with
the test functions, the suite also specifies a detailed
protocol how to evaluate a search heuristic: the prob-
lem dimension ranges from n = 10. ..50, the number
of allowed function evaluations is restricted to n· 10
4
,
A TUNABLE REAL-WORLD MULTI-FUNNEL BENCHMARK PROBLEM FOR EVOLUTIONARY OPTIMIZATION
- And Why Parallel Island Models Might Remedy the Failure of CMA-ES on It
249

measures for success performance are defined, and
examples of how to present the results in tables and
figures are provided. We refer to the original publi-
cation for the full description of the test suite (Sugan-
than et al., 2005). Here, we use functions f11 to f13,
f15, and f16 to evaluate the performance of IPOP- and
PS-CMA-ES on multi-funnel problems.
2.2 Lennard-Jones Clusters
The PES of Lennard-Jones (LJ) clusters is one of the
best studied models both in physical chemistry and,
to some extent, in the field of global optimization.
The objective of finding the minimum-energy config-
uration of this model has fascinated researchers from
both communities for over three decades. Each pair
of atoms in a LJ cluster interacts through the LJ pair
potential
u(r
ij
) = 4ε
σ
LJ
r
ij
12
−
σ
LJ
r
ij
6
!
, (1)
where r
ij
is the distance between atoms X
i
and X
j
,
ε the potential-well depth (in units of energy) and
2
1
6
σ
LJ
the equilibrium inter-atom distance (in units of
length) at zero temperature. The potential energy E
LJ
of a cluster of N LJ atoms is given by:
E
LJ
= 4ε
N−1
∑
i=1
N
∑
j=i+1
σ
LJ
r
ij
12
−
σ
LJ
r
ij
6
!
. (2)
In chemistry, the LJ potential is widely used to model
hydrophobic interactions in polymers or the behav-
ior of (noble) gases such as Argon. Knowledge about
minimum-energy (or ground-state) configurations of
LJ clusters enables, e.g., predicting properties of crys-
tallization or solid–liquid transitions at low temper-
atures. At the same time, LJ clusters are a model
problem for general-purpose non-convex optimiza-
tion. Minimizing the potential energy of a cluster of N
atoms in 3D space defines a continuous optimization
problem in 3N − 6 dimensions since 3 translational
and 3 rotational degrees of freedom can be removed
from the system. This is achieved by placing the first
atom at the origin of the Cartesian coordinate system,
the second along the x-axis and the third in the x− −y
plane. Several general-purpose optimizers have been
tested on LJ clusters of various sizes, most notably the
Basin Hopping algorithm (Wales and Doye, 1997),
which makes extensive use of gradient information.
To date, finding the minimum-energyconfiguration of
LJ clusters is only feasible for global search heuris-
tics that are allowed to exploit exact, analytical gra-
dients. All known putative minimum-energy configu-
rations are listed in the Cambridge Cluster Database,
providing a valuable resource for optimization bench-
marks. A particularly well-understood configuration
is the 38-atom cluster, forming the basis for the new
benchmark problem proposed here.
2.2.1 The Energy Landscape of the 38-atom
Lennard-Jones Cluster
The topology of the LJ
38
PES has been extensively
studied in the literature (Doye et al., 1999; Doye,
2000; Wales, 2004). It exhibits a double-funnel struc-
ture where the global minimum-energy configuration
with face-centered cubic octahedral (fcc) symmetry
lies in a narrow funnel and the majority of local min-
ima, all with icosahedral (ico) symmetry, populate the
wider funnel. Figure 1 shows a sketch of the land-
scape.
Potential Energy
Order Parameter
ico
fcc
Funnel 1
Funnel 2
Figure 1: Sketch of the PES of the 38-atom LJ cluster. The
x-axis represents a suitable order parameter that can dis-
criminate between different cluster topologies, the y-axis
represents the potential energy of the configurations. The
wide funnel on the left is populated by clusters with icosa-
hedral (ico) symmetry. The lowest-energy configuration
with ico symmetry is depicted in blue. The narrow fun-
nel on the right contains the global minimum with face-
centered cubic octahedral (fcc) symmetry (depicted in red).
(Doye et al., 1999) characterized this landscape in
great detail in terms of the number and locations of
minima, structural diversity of the minima, and the
energy barrier between the two funnels. In a subse-
quent study, (Doye, 2000) also studied the effect of
compression on the PES of the 38-atom LJ cluster.
Compression can be seen as a transformation of the
PES that favors more compact structures. Hence, it
broadens the funnel of the more spherical fcc struc-
tures and narrows the ico funnel. Doye added the fol-
lowing compression penalty to the energy function:
E
CLJ
= E
LJ
+ µ
comp
N
∑
i=1
kX
i
− X
cm
k
2
σ
2
LJ
, (3)
IJCCI 2009 - International Joint Conference on Computational Intelligence
250

where X
i
is the position of atom i and X
cm
is the center
of mass of the cluster. The parameter µ
comp
controls
the magnitude of the compression acting on the con-
figuration. When µ
comp
≥ 5ε, the PES of the cluster
exhibits a clear single-funnel topology. The effect of
the µ
comp
-dependent compression on the PES is beau-
tifully visualized in (Wales, 2004), pp. 338–339, and
(Doye, 2000). Note that even with the compressed
potential E
CLJ
the system contains a staggering num-
ber of local minima, but the global topology can be
changed from double-funnel to single-funnel. This
renders the 38-atom LJ cluster with tunable compres-
sion an ideal real-world test case to study the perfor-
mance of evolutionary algorithms and their sensitivity
to the underlying topology.
2.2.2 Bond-order Parameters for Cluster
Characterization
Bond-order parameters are indispensable for the anal-
ysis of cluster configurations (Steinhardt et al., 1983).
These parameters, termed Q
4
, Q
6
, W
4
, andW
6
are able
to discriminate symmetry groups in crystals and liq-
uids. The parameters Q
4
and Q
6
have been identi-
fied as the most informative ones for distinguishing
fcc from ico configurations. Q
l
is defined as:
Q
l
=
4π
2l + 1
l
∑
m=−l
k
¯
Q
lm
k
2
!
1
2
, (4)
where
¯
Q
lm
=
1
N
b
∑
r
ij
<r
0
Y
lm
(Θ
ij
,Φ
ij
). (5)
Here, N
b
denotes the number of pseudo bonds that
have a length smaller than a cutoff distance r
0
.
Y
lm
(Θ
ij
,Φ
ij
) are spherical harmonics with Θ
ij
being
the polar and Φ
ij
the azimuthal angle of the inter-
atomic vector r
ij
with respect to an arbitrary coordi-
nate frame. We propose to use the order parameter
Q
4
with a cutoff of r
0
= 1.391σ
LJ
as suggested for
LJ cluster analysis (Doye et al., 1999). A Q
4
value
of 0 corresponds to a perfect icosahedron, a value of
0.1909 to a perfect fcc configuration.
3 STANDARD CMA-ES AND
PARALLEL-ISLAND CMA-ES
This section reviews (IPOP-)CMA-ES and parallel is-
land models for CMA-ES.
3.1 The CMA Evolution Strategy
The standard CMA-ES uses weighted intermediate
recombination, step size adaptation, and a combina-
tion of rank-µ update and rank-one update (Hansen
and Ostermeier, 2001; Hansen, 2007). At each itera-
tion of the algorithm, the members of the new popula-
tion are sampled from a multivariate normal distribu-
tion N with mean m ∈ R
n
and covariance C ∈ R
n×n
.
The sampling radius is controlled by the overall stan-
dard deviation (step size) σ. Let x
(g)
k
the k
th
individ-
ual at generation g. The new individuals at generation
g+ 1 are sampled as:
x
(g+1)
k
∼ m
(g)
+ σ
(g)
N
0,C
(g)
k = 1,. ..,λ. (6)
The λ sampled points are then ranked in order of as-
cending fitness, and the µ best are selected. The mean
of the sampling distribution is updated using weighted
intermediate recombination (Hansen, 2007). The
covariance matrix is adapted as described in vari-
ous publications and reports (Hansen and Ostermeier,
2001; Hansen, 2007). The behavior of CMA-ES is
mainly controlled by two parameters: the initial step
size σ and the population size λ. In standard CMA-
ES, the population size is chosen as λ = 4 + ⌊3lnn⌋
(Hansen and Ostermeier, 2001). The most success-
ful variant of CMA-ES, IPOP-CMA-ES, employs a
restart mechanism with iterative doubling of the pop-
ulation size until a stopping criterion is met (Auger
and Hansen, 2005). It uses an initial step size of
σ = (B − A)/2, where [A,B]
n
is the bounded search
space. These standard choices render IPOP-CMA-ES
quasi parameter-free.
3.2 Parallel Island Models for CMA-ES
The concept of parallel island models for evolution-
ary algorithms is to use a set of independent (possi-
bly heterogeneous) populations (islands) that concur-
rently explore the problem space. During search, the
populations are allowed to migrate (communicate in-
formation)in an (a-)synchronousway. Many different
migration patterns and modes of information sharing
have been examined in recent years. Two advantages
of parallel island models are that (a) different distant
parts of the search space can be explored simultane-
ously and integrated into individual populations, and
(b) such algorithms can easily be parallelized in a dis-
tributed computing environment. For detailed infor-
mation on the topic, we refer to (Alba, 2005).
A specific instance of a parallel island model for
CMA-ES, the Particle Swarm CMA-ES (M¨uller et al.,
2009), has been introduced in order to improve the
performance of CMA-ES on multi-funnel landscapes.
Inspired by ideas from Particle Swarm Optimization
(PSO), the PS-CMA-ES algorithm evolves a swarm
of S CMA-ES instances in parallel. The individual
A TUNABLE REAL-WORLD MULTI-FUNNEL BENCHMARK PROBLEM FOR EVOLUTIONARY OPTIMIZATION
- And Why Parallel Island Models Might Remedy the Failure of CMA-ES on It
251

instances exchange promising solutions every I
c
gen-
erations. Both the swarm size S (the total number of
concurrent CMA-ES instances) and the communica-
tion interval I
c
are strategy parameters. The influence
of global swarm information on the covariance matrix
adaptation of each CMA-ES instance is controlled by
a weight parameter c
p
∈ [0,1]. A detailed description
of the algorithm can be found in (M¨uller et al., 2009).
4 COMPUTATIONAL
EXPERIMENTS
We first show the performance of IPOP-CMA-ES on
LJ
38
and then assess IPOP- and PS-CMA-ES on a
multi-funnel subset of the CEC 2005 test suite.
4.1 The 38-Atom LJ Cluster
We search for the minimum-energy configurations of
LJ
38
in a 3D [−4,4] box. The search space thus is
[−4,4]
n
with dimension n = 3· 38− 6 = 108. The LJ
parameters σ
LJ
and ε are both set to 1. In order to as-
sess the effectiveness of IPOP-CMA-ES on LJ
38
, we
follow the parameterization and boundary handling of
(Auger and Hansen, 2005) with two important excep-
tions. Instead of doubling the population size after
each restart, we increase λ by a factor of 1.25. We
also refine the initialization procedure in order to as-
sess the effect of initial LJ-particle positions on the
quality of the solution: We place the initial popula-
tion mean uniformly random in the box [−0.5,0.5]
3
,
[−1.5,1.5]
3
, or [−3,3]
3
and sample the initial popu-
lation with a σ of 20% of the box edge length. We
repeat the experiment 25 times for each box size with
no bounds on the number of allowed function evalua-
tions. We stop an optimization run whenever the pop-
ulation size exceeds the initial λ by a factor of 100,
i.e., after 21 restarts. We consider LJ
38
clusters with-
out compression and with µ
comp
= 5ε.
Figure 2 summarizes the results. The experiments re-
veal that on the LJ
38
problem without compression
none of the IPOP-CMA-ES runs reach the lowest-
energy fcc configuration, nor the lowest-energy ico
configuration (blue in Figure 2), despite the fact
that each run used, on average, 10
8
function evalua-
tions. With compression, however, all IPOP-CMA-
ES runs find the globally optimal fcc configura-
tion, independent of initialization. Even more strik-
ingly, all local minima found on the problem with-
out compression have icosahedral-like configurations
with Q
4
values between 0.01 and 0.045. The runs
that started in the largest box (blue •’s in Fig. 2)
show the largest structural diversity of the minima
!" !# !$ ! !% &' &( &!
%
%)%$
%)%"
%)%&
%)%(
%)
%) $
%) "
%) &
%) (
%)$
Energy
[
ǫ
]
Q
4
Structural transition regio
n
Figure 2: Bond-order parameter Q
4
vs. potential energy
(in units of ε) for all minima found by IPOP-CMA-ES.
The blue data points show the 3 · 25 local minima found
on the LJ
38
problem without compression with the ini-
tial [−0.5,0.5]
3
box (×), the [−1.5,1.5]
3
box (◦), and the
[−3,3]
3
box (•). The single blue in the bottom-left cor-
ner marks the lowest-energy icosahedral configuration. The
shaded gray area is the structural transition region from ico
to fcc symmetry (Doye et al., 1999). The red data point
in the upper-left corner corresponds to the global minimum
(E
LJ
= −173.9284ε), which was found by IPOP-CMA-ES
in all 3· 25 runs when using the compression penalty.
(Q
4
= 0.01. ..0.045), including the lowest local min-
imum found at E
LJ
≈ −170.66ε. All runs that started
in the [−1.5,1.5]
3
box converged to the same local
minimum, while the runs in the smallest box found
an additional local minimum.
4.2 The IEEE CEC 2005 Test Suite
We provide evidence that the failure of IPOP-CMA-
ES on multi-funnel functions can be remedied by us-
ing a parallel island model instead of a single popu-
lation of increasing size. Therefore, we compare the
performanceof the parallel island PS-CMA-ES to that
of IPOP-CMA-ES on the multi-funnel functions f11
to f13, f15, and f16 of the CEC 2005 benchmarksuite.
The results are summarized in Table 1. All experi-
ments are conducted according to the CEC 2005 pro-
tocol. While IPOP-CMA-ES is still quite efficient on
the modified Weierstrass function (f11) and Schwe-
fel’s problem (f12), it is not able to solve any of the
other multi-funnel functions in the set. PS-CMA-ES
can solve f11 to f13 with strategy parameters c
p
= 0.7,
I
c
= 200, and S = 15, and f15 and f16 with strat-
egy parameters c
p
= 0.3, I
c
= 150, and S = 10. To
our knowledge, no other algorithm has so far been re-
ported to solve the pair f15/f16.
IJCCI 2009 - International Joint Conference on Computational Intelligence
252
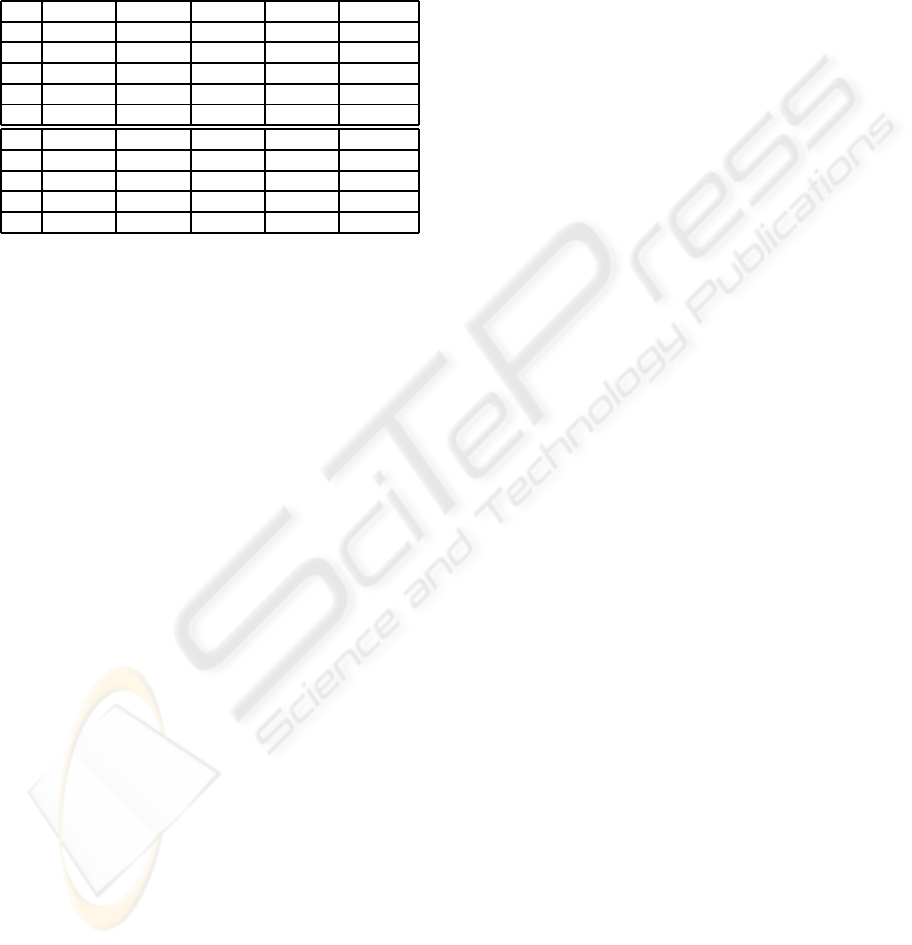
Table 1: Summary statistics of IPOP-CMA-ES (first block,
taken from (Auger and Hansen, 2005)) and PS-CMA-ES
(second block) on the multi-funnel functions f11 to f13,
f15, and f16 of the CEC 2005 test suite in n = 10 dimen-
sions. The minimum, median, maximum, and mean num-
ber of function evaluations needed to solve the problems
are reported over 25 repetitions of each test. The last col-
umn reports the success rates. See main text for strategy
parameters used.
min med max mean Suc. Rate
f11 3.05e+04 - - 6.31e+4 2.40e-01
f12 2.37e+03 3.10e+04 - 2.88e+04 8.80e-01
f13 - - - - 0
f15 - - - - 0
f16 - - - - 0
f11 3.56e+04 - - 5.02e+04 4.00e-01
f12 1.66e+04 1.89e+04 2.13e+04 1.92e+04 1.00e+00
f13 8.34e+04 - - 8.34e+04 4.00e-02
f15 3.30e+04 - - 3.65e+04 1.20e-01
f16 5.09e+04 - - 5.09e+04 4.00e-02
5 CONCLUSIONS
In summary, we have proposed: (a) a tunable real-
world multi-funnel test case for gradient-free evolu-
tionary optimizers and (b) that parallel island models
can relax the performance decrease of CMA-ES on
multi-funnel functions where the global optimum is
not located in the broadest funnel. The latter can be
explained by the irresolvable trade-off for the optimal
population size of CMA-ES on multi-funnelfunctions
(Lunacek et al., 2008). The larger the population size,
the more likely CMA-ES converges in the broadest,
sub-optimal funnel. This is supported by the fact that
IPOP-CMA-ES performs remarkably well when the
PES of LJ
38
is compressed to a single-funnel structure
and that the parallel island PS-CMA-ES outperforms
IPOP-CMA-ES on the considered sub-set of multi-
funnel functions from the CEC 2005 test suite. To
date, no population-based, gradient-free evolutionary
algorithm can solve the presented LJ
38
test case with-
out compression. Since many real-world applications
entail multi-funnel landscapes, we argue that the EC
community should focus on algorithms that can solve
such problems. As a benchmark, we suggest the LJ
38
problem, which should be considered in all future EC
studies that introduce a novel general-purpose opti-
mizer.
ACKNOWLEDGEMENTS
We thank Georg Ofenbeck for setting up the LJ cluster
simulations.
REFERENCES
Alba, E. (2005). Parallel Metaheuristics: A New Class of
Algorithms. Wiley-Interscience.
Auger, A. and Hansen, N. (2005). A restart CMA evolu-
tion strategy with increasing population size. In Proc.
IEEE Congress on Evolutionary Computation (CEC
2005), volume 2, pages 1769–1776.
Clark, P. L. (2004). Protein folding in the cell: reshaping
the folding funnel. Trends Biochem. Sci., 29(10):527–
534.
Doye, J. (2000). Effect of compression on the global opti-
mization of atomic clusters. Phys. Rev. E, 62(6, Part
B):8753–8761.
Doye, J. P. K., Miller, M. A., and Wales, D. J. (1999).
The double-funnel energy landscape of the 38-atom
Lennard-Jones cluster. J. Chem. Phys., 110(14):6896–
6906.
Hansen, N. (2007). The CMA Evolution Strategy: A Tuto-
rial. http://www.lri.fr/ hansen/cmatutorial.pdf.
Hansen, N. and Kern, S. (2004). Evaluating the CMA Evo-
lution Strategy on Multimodal Test Functions. In Lect.
Notes Comput. Sc., volume 3242 of Parallel Problem
Solving from Nature - PPSN VIII, pages 282–291.
Hansen, N. and Ostermeier, A. (2001). Completely Deran-
domized Self-Adaption in Evolution Strategies. Evo-
lutionary Computation, 9(2):159–195.
Lunacek, M., Whitley, D., and Sutton, A. (2008). The Im-
pact of Global Structure on Search. In Lect. Notes
Comput. Sc., volume 5199 of Parallel Problem Solv-
ing from Nature - PPSN X, pages 498–507.
M¨uller, C. L., Baumgartner, B., and Sbalzarini, I. F. (2009).
Particle swarm CMA evolution strategy for the opti-
mization of multi-funnel landscapes. In Proc. IEEE
Congress on Evolutionary Computation (CEC 2009),
pages 2685–2692.
Steinhardt, P. J., Nelson, D. R., and Ronchetti, M. (1983).
Bond-orientational order in liquids and glasses. Phys.
Rev. B, 28(2):784–805.
Suganthan, P. N., Hansen, N., Liang, J. J., Deb, K., Chen,
Y.-P., Auger, A., and Tiwari, S. (2005). Problem Defi-
nitions and Evaluation Criteria for the CEC 2005 Spe-
cial Session on Real-Parameter Optimization. Techni-
cal report, Nanyang Technological University, Singa-
pore.
Sutton, A. M., Whitley, D., Lunacek, M., and Howe, A.
(2006). PSO and multi-funnel landscapes: how co-
operation might limit exploration. In Proc. ACM
Genetic and Evolutionary Computation Conference
(GECCO’06), pages 75–82. ACM.
Wales, D. (2004). Energy Landscapes : Applications
to Clusters, Biomolecules and Glasses (Cambridge
Molecular Science). Cambridge University Press.
Wales, D. J. and Doye, J. P. K. (1997). Global Optimiza-
tion by Basin-Hopping and the Lowest Energy Struc-
tures of Lennard-Jones Clusters Containing up to 110
Atoms. J. Phys. Chem. A, 101(28):5111–5116.
A TUNABLE REAL-WORLD MULTI-FUNNEL BENCHMARK PROBLEM FOR EVOLUTIONARY OPTIMIZATION
- And Why Parallel Island Models Might Remedy the Failure of CMA-ES on It
253
