OBSERVATION WITH BOUNDS OF BIOLOGICAL SYSTEMS

A Linear Programming Approach

Fernando Tadeo and Mustapha Ait Rami

Dpto. Ingenieria de Sistemas y Automatica, Universidad de Valladolid, 47005 Valladolid, Spain

Keywords:

Compartmental models, Observers, Linear Programming, Kinetic models.

Abstract:

This paper presents a technique to estimate the states of biological systems that cannot be directly measured,

by using available measurements of other states that affect them. More precisely, the proposed technique

makes it possible to derive, at each moment, the possible range of variation of these unmeasured states. It is

based on having a compartmental model of the system (which might include uncertain parameters), and then

solving a Linear Programming problem. A practical example, based on the kinetic model of drug distribution

through the human body, is provided to show its applicability.

1 INTRODUCTION

It is well known that most biological systems can be

represented mathematically in quite a precise way by

compartmental models (Jacquez, 1985). The main

characteristic of these compartmental systems is that

that the internal states are nonnegative by nature, as

they represent concentrations, temperatures, cell birth

or losses, etc: See (Hynne et al., 2001; Luzyanina

et al., 2007; Linninger et al, 2009) and references

therein for many practical examples.

Thus, this paper considers the compartmental ob-

servation problem, which consists of constructing

compartmental observers (Vanden Hof, 1998), that is,

observers that ensure the compartmental properties of

the states (i.e., positivity and conservation). These ob-

servers are very important in biological systems: stan-

dard observers and ﬁlters provided by systems theory

(Luenberger, 1966; Gover and Brown, 1992), if they

are not designed taking into account the characteris-

tics of compartmental systems, might give some neg-

ative values, which are completely illogical (those ob-

servers might, for example, estimate that certain con-

centrations are negative). The method presented here,

which circumvents this problem, is based on some re-

cent results on the theory of positive observers (Ait

Rami et al, 2007a; Ait Rami et al., 2007b), which can

be applied to compartmental models. These results

are used here to provide conditions for the observa-

tion of biological systems described by compartmen-

tal models, providing a simple approach to numeri-

cally address the determination of compartmental ob-

servers (as linear programs can be solved easily using

off-the-shelf software).

Moreover, the proposed compartmental observers

can be used to obtain tight upper and lower bounds on

the estimated variables, even in the presence of uncer-

tain parameters in the model. That is, if bounds on the

initial states of the observed system are known, and

uncertainty in the system matrices can be evaluated,

which is common in practice, the evolution of the un-

measured states will always be between the estimated

bounds, providing a bounding observer. Moreover,

these estimated bounds converge to the real value,

and, compared to previous approaches for bounding

observers (Gouze et al., 2000; Rapaport, 2005; Alamo

et al, 2005), the proposed observer is simple to im-

plement, and the design of the observer parameters

is based on straightforward conditions (this design is

based on solving simple Linear Programming condi-

tions).

The proposed approach is directly applicable to

many systems in biology (including medicine), such

as those in (Hynne et al., 2001; Luzyanina et al., 2007;

Linninger et al, 2009). As an example, the kinetic

models of the bone-seeking radiopharmaceutical Tc-

99m(Sn)methylenediphosphonate (Tc-MDP) in adult

humans, that were derived in (Makler and Charkes,

1980), are used here to present the problem, and show

that, by using the proposed approach, it is possible

to provide tight estimations of the unmeasured states,

giving upper and lower bounds on the real states.

The paper is organized as follows: Section 2

presents the example that will be used as case study,

230

Tadeo F. and Ait Rami M. (2010).

OBSERVATION WITH BOUNDS OF BIOLOGICAL SYSTEMS - A Linear Programming Approach.

In Proceedings of the Third International Conference on Bio-inspired Systems and Signal Processing, pages 230-235

DOI: 10.5220/0002717602300235

 SciTePress

Section 3 gives the structure of the proposed bound-

ing observer and a methodology to select the observer

parameters. Finally, Section 4 presents a complete ap-

plication to the case study, and some conclusions are

given.

2 MOTIVATING EXAMPLE

An example is now given to show the kind of prob-

lems we want to solve: Kinetic models are frequently

used to determine doses of drugs in radiotherapy. For

instance, the short-lived bone-seeking radiopharma-

ceutical

99m

Tc-methylene diphosphonate (Tc-MDP)

is used in bone imaging for investigating the state

of the skeleton in diffuse metabolic bone diseases

(osteoporosis, hyperparathyroidism) or at local ab-

normalities in metastatic bone disease (Blake et al.,

2002). Based on clinical measurements in adult hu-

mans, the portion of the administered dose of Tc-

MDP in some compartments of the human body was

determined (Makler and Charkes, 1980) to be pre-

cisely given by the following compartmental model:







-k

− k

0 k

-k

0 0

0 k

-k

0 0

0 0 -k

0 0 0 -k







x(t),

y(t) =



c 0 0 0 0



x(t).

(1)

where the vector x(t) contains the states, that cor-

respond to the portion of the dose of the Tc-MDP

tracer in the different compartments: x

(t) is the por-

tion of the dose in the blood, x

(t) in the bone-ECF,

(t) in normal bone, x

(t) in the tubular urine and

(t) in the rest of the human body. Some values for

the parameters of the model were obtained from phys-

iological data. Our objective is to provide a technique

that uses this mathematical model and the available

information on the parameters to design an observer

that gives time-dependent upper and lower bounds on

the portions in the different compartments. The esti-

mations will be continuously updated based on mea-

surements of the dose in the blood just after an in-

jection (this is the only measurement that is assumed

here to be available, but the technique can be directly

extended to other measurements).

Model (1) corresponds to the general class of pos-

itive (compartmental) systems described by

= Ax(t), y(t) = Cx(t), x(0) ≥ 0. (2)

It is well known (Luenberger, 1966) that the ob-

servation of the states of dynamical systems described

by (2)) can be based on using a classical Luenberger

observer, that consists of integrating the linear differ-

ential equations, starting from adequate initial condi-

tions, of the following dynamical system:

dΘ

= (A− LC)Θ(t) + Ly(t).

(3)

The observer design is then based on selecting a ma-

trix L that gives closed-loop stability and some per-

formance. This design is frequently based on placing

the eigenvalues of the matrix A− LC in desired posi-

tions. Once L is selected, it is only necessary to in-

tegrate (3), starting from adequate initial conditions,

to get estimations that converge to the real state: this

simplicity of concept and implementation has made

Luenberger observers useful for those practical appli-

cations where the system can be precisely described

by a dynamical system.

Unfortunately, the Luenberger observer in (3)

does not take into account the fact that the system

(2) is compartmental, so unrealistic results might be

(temporarily) obtained for some of the states.

Moreover, in many applications, it is important to

ensure upper and/or lower bounds on the real states,

but standard Luenberger observers do not ensure that

the estimated states converge from above (or from be-

low) to the real states.

Another problem of classical observers is that the

uncertainty in the system parameters or the initial

state cannot be easily incorporated into the observer:

For example, clinical trials detected a variation be-

tween individuals between 0.502 and 0.578 for k

whereas k

was found to vary between 1.018 and

1.092. Methodologies to include this information

for designing the observer are available but are quite

complex (Gouze et al., 2000; Combastel, 2005; Rapa-

port, 2005). Our objectiveis to give a general method-

ology that is simple to apply and does not need in-

volved calculations.

Thus, this paper concentrates on providing a prac-

tical methodology to estimate states for biological

systems, that can be described by (2), which ensures

that the estimated states are logical (i.e., never nega-

tive), provide tight bounds on the estimated variables,

and takes into account uncertain parameters. This

proposed methodology is described in the next sec-

tion.

OBSERVATIONWITH BOUNDS OF BIOLOGICAL SYSTEMS - A Linear Programming Approach

231

3 PROPOSED BOUNDING

OBSERVER

We assume that the system whose states are to be es-

timated on-line can be described as a compartmen-

tal system (maybe including uncertain parameters),

where there are p measured variables (that form the

column vector y(t)) and n internal states (that describe

each compartment, and form the state vector x(t)).

More precisely, we consider models that can be de-

scribed by the following linear dynamical model:

˙x(t) = Ax(t), y(t) = Cx(t), x(0) ≥ 0 (4)

Thus, the square constant matrix A is composed of

n × n elements (that will be denoted by a

), and the

constant matrix C has n rows and p columns of el-

ements denoted by c

. These matrices are assumed

to be uncertain, but they can be bounded by known

matrices A, A, C and C, such that

A ≤ A ≤ A and C ≤ C ≤ C. (5)

Mathematically, system (4) is said to be compartmen-

tal if the matrix A does not have negative off-diagonal

elements (it is called a Metzler matrix) and satisﬁes

the following property:

∑

i=1

≤ 0. (6)

It is assumed that bounds on the initial state are

known: x ≤ x(0) ≤ x. In the uncertain case A does

not have negative off- diagonal elements, but A and

A probably do not fulﬁll the property (6): they pro-

vide a positive system, but probably not a compart-

mental one. As has been discussed in Section 2, clas-

sical observers are not adequate for compartmental

systems, specially in the presence of uncertainty in

the parameters of the system. Thus, we propose to

incorporate to the observer the available information

on the system uncertainties, by using an observer that

gives upper and lower bounds on the real states. This

makes it possible to incorporate uncertainty into the

initial states of the system, as they are never perfectly

known. The proposed approach is based on using an

observer with two independent sets of states: one set

(denoted Θ) is used to derive an upper bound on the

real state, whereas the other set (Θ) makes it possible

to derive a lower bound.

The proposed observer is then given by the fol-

lowing two independent dynamical equations:

dΘ

= (A− LC)Θ(t) + Ly(t),

dΘ

= (A− LC)Θ(t) + Ly(t).

(7)

The states are then estimated by integrating (7), start-

ing from adequate initial conditions. The design is

then based on estimating an observer gain L which

ensures that

1) both sets of dynamical equations in (7) are stable,

2) the integration of the dynamical equations evolve

towards the real state,

3) the states are always between Θ(t) and Θ(t)

4) the lower bound Θ(t) is always nonnegative, pro-

vided that the initial condition is nonnegative.

To characterize the set of observer gains that fulﬁll

these properties the following condition is proposed

(based on the results in (Ait Rami et al., 2007b)):

There exists a bounding observer of system (4) of the

form (7) if and only if the following Linear Program

has a solution:











λ−C

∑

i=1

< 0,

≥ 0 for i, j = 1, . . . , n,

− c

≥ 0 for i 6= j,

λ > 0.

(8)

The variables of this Linear Programming prob-

lem are λ = [λ

. . . λ

]

∈ R

and z

, . . . , z

∈ R

whereas L can be obtained from any feasible solution

of this LP problem:

L =







...







. (9)

To clarify the notation, a

are the elements of the ma-

trix A, c

are the columns of C, etc. It must be pointed

out that the proposed approach can be extended to re-

lated problems, such as compartmental systems with

delays (Ait Rami et al., 2007b), discrete-time systems

(Ait Rami et al, 2007a), disturbances, etc.

4 APPLICATION TO THE

EXAMPLE

Based on clinical measurements (Makler and

Charkes, 1980) obtained the following parameters

for the compartmental model (1), including vari-

ability in the parameters: k

= 0.540 ± 0.038,

= 0.095 ± 0.003, k

= 0.277 ± 0.007,

= 0.431 ± 0.011, k

= 0.233, k

= 0.024,

= 0.049 ± 0.001, and k

= 1.055 ± 0.037. To

take into account the unavoidable measurement errors

we ﬁx c = 1± 0.05.

BIOSIGNALS 2010 - International Conference on Bio-inspired Systems and Signal Processing

232

Based on the result presented in the previous sec-

tion, the Linear Programming problem (3) can be eas-

ily solved to obtain a compartmental observer with the

following observer gain:

L =



12 0.0365 0.005 0.335 0.024



. (10)

It is now shown how the compartmental observer (7),

with this gain, can be used to provide upper and lower

bounds on the estimated states, taking also into ac-

count the unavoidable uncertainty in the system pa-

rameters and initial conditions.

For simulation, assume that the concentration in

the blood is continuously measured, shortly after in-

jection, so the conditions of the system when the

observation starts are bounded within the following

range:







y(0) − 0.05







≤ x(0) ≤







y(0) + 0.05

0.2

0.3

0.6

0.04







. (11)

with y(0) the ﬁrst measurement of the dose in blood.

Thus, to get a bounding observer, the initial

condition of the lower observer states is Θ(0) =



y(0) − 0.05 0 0 0 0



, whereas the initial

condition of the upper observer states is Θ(0) =



y(0) + 0.05 0.2 0.3 0.6 0.04



. By the re-

sult in Section 3, the evolution of the state x(t) will

always be between the estimated states Θ(t) ≥ 0 and

Θ(t). Moreover,these estimations converge to the real

value, and are always nonnegative.

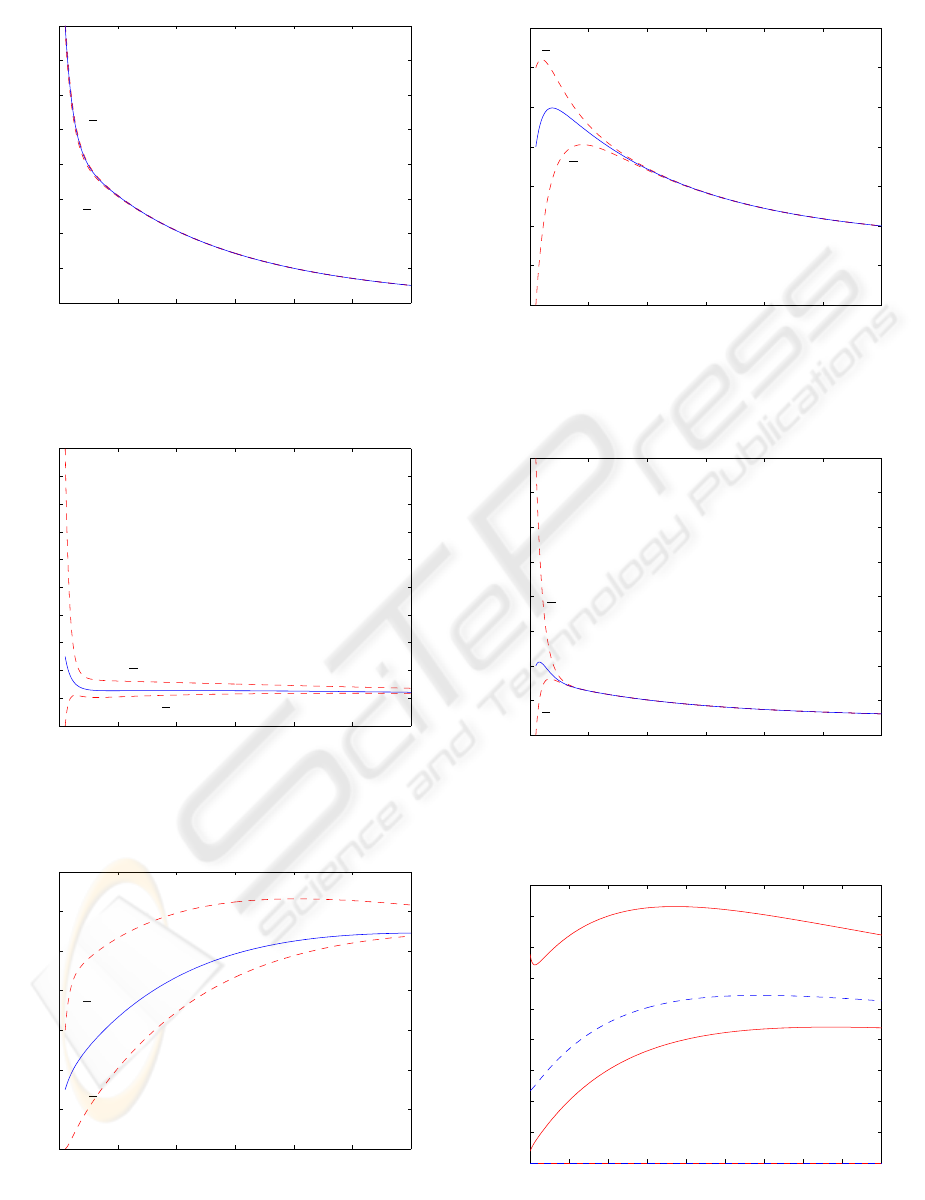
These claims can be conﬁrmed in Figures 1 to

5, which plot the state evolutions for the parame-

ters obtained for one of the patients in the origi-

nal study, starting from the initial conditions (x(0) =



0.5 0.05 0.15 0.4 0.01



), when the dos-

ing has ﬁnished (i.e., with null input), together with

the bounds estimated using the approach proposed

in Section 3 and the gain (11). For simplicity, it is

assumed that the system parameters remain constant

throughout the experiment (the plant parameters cor-

respond to mean values) and there is no measurement

noise. It is possible to see that the estimated states are

nonnegative and converge to the real values, giving

lower and upper bounds on the real states that con-

verge to the real values.

Thus, for example, using the proposed approach,

it is possible to give tight estimations of the concen-

tration of in the bone-ECF (see Figure 2), despite the

uncertain initial conditions, and the person-to-person

variations in the nominal parameters: for example, in

Figure 2, it is possible to see that just two minutes

after the start of measurements of the concentration

of Tc-MDP in the blood it is possible to predict pre-

cisely that the portion of dose in the bone-ECF will be

greater than 0.022 and smaller than 0.037, whereas for

the non-bone-ECF ten minutes are enough to estimate

the portion of dose with a 10% accuracy.

These estimations can be easily used to derive the

ﬁgures of merits usually used to derive imaging times.

In this case, the objective is to distinguish, in the im-

ages, the bone from the surrounding tissue, so, fol-

lowing common practice, we deﬁne the target to be

= 0.1x

+ x

, (assuming a 10% of blood vol-

ume in the skeleton), whereas the background is pro-

vided to be Q

= 0.9x

+ x

. This makes it possible

to easily derive bounds on ﬁgures of merits frequently

used, such as the contrast, shown in Figure 6:

Contrast =

, (12)

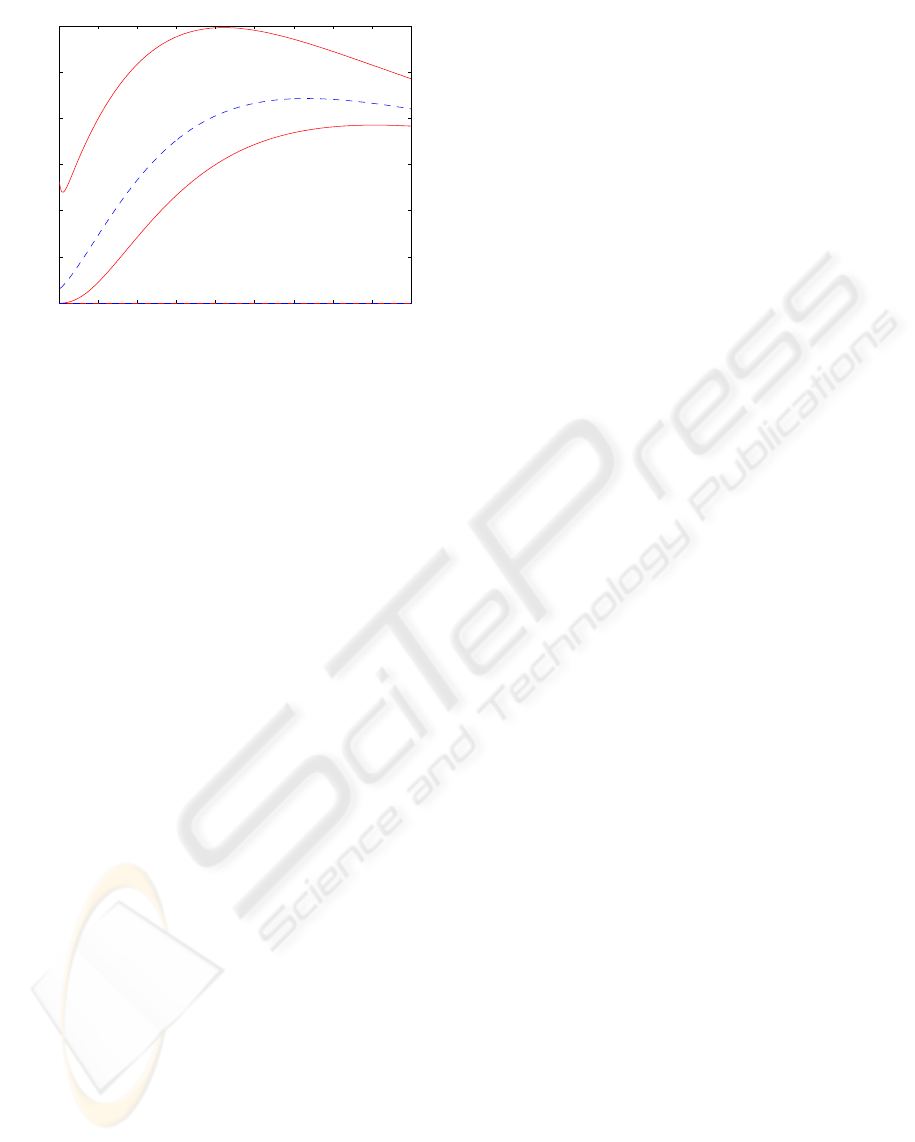
or the relative contribution of target and background,

depicted in Figure 7, which statistically corresponds

to the Beck-Harper ﬁgure of merit:

Q =

−C

)

. (13)

The obtained results agree with those obtained in

practice (Subramanian et al., 1975; Rosenthall et al.,

1997; Fogelman et al, 1979).

We must point out that parallel results can be ob-

tained when dosing is measured in the urine, maybe

simultaneously with measurement in the blood, fol-

lowing the same procedure, and it is directly applica-

ble to other tracers used in medical imaging, such as

F-Fluoride (Cook et al., 2000). Moreover, the pro-

posed methodology is general, as the only property

used is the fact that the system can be described as a

compartmental model with uncertainty (which is the

case of most biological systems (Jacquez, 1985)).

5 CONCLUSIONS

This paper has proposed a new approach to solve the

observation problem for compartmental models in bi-

ology, by providing upper and lower bounds on the

unmeasured states, which incorporates uncertainty in

the parameters and initial conditions of the system.

This problem has been studied, and a simple nec-

essary and sufﬁcient condition for its solvability has

been proposed, based on solving a Linear Program-

ming Problem. An illustrative case study, based on a

radiopharmaceuticalproblem, shows the feasibility of

the proposed approach, and how it can be used to de-

rive upper and lower bounds on the estimated states.

OBSERVATIONWITH BOUNDS OF BIOLOGICAL SYSTEMS - A Linear Programming Approach

233

0 10 20 30 40 50 60

0.1

0.15

0.2

0.25

0.3

0.35

0.4

0.45

0.5

State 1, with bounds given by the proposed observer

−

[1]

x[1]

−[1]

t (minutes)

Portion of dose

Figure 1: Evolution of the concentration in the blood, and

estimated bounds.

0 10 20 30 40 50 60

0.02

0.04

0.06

0.08

0.1

0.12

0.14

0.16

0.18

0.2

State 2, with bounds given by the proposed observer

−[2]

x[2]

−[2]

t (minutes)

Portion of dose

Figure 2: Evolution of the concentration in the bone-ECF,

and estimated bounds.

0 10 20 30 40 50 60

0.1

0.2

0.3

0.4

0.5

0.6

0.7

State 3, with bounds given by the proposed observer

−

[3]

x[3]

−[3]

t (minutes)

Portion of dose

Figure 3: Evolution of the concentration in the bone, and

estimated bounds.

0 10 20 30 40 50 60

0.1

0.2

0.3

0.4

0.5

0.6

0.7

State 4, with bounds given by the proposed observer

−

[4]

x[4]

−[4]

t (minutes)

Portion of dose

Figure 4: Evolution of the concentration in the non-bone-

ECF, and estimated bounds.

0 10 20 30 40 50 60

0.005

0.01

0.015

0.02

0.025

0.03

0.035

0.04

State 5, with bounds given by the proposed observer

−[5]

x[5]

−[5]

t (minutes)

Portion of dose

Figure 5: Evolution of the concentration in the urine, and

estimated bounds.

0 10 20 30 40 50 60 70 80 90

Contrast: estimated worst−case bounds

t(min)

%uncorrected dose (uncorrected)

Figure 6: Contrast, with estimated bounds.

BIOSIGNALS 2010 - International Conference on Bio-inspired Systems and Signal Processing

234

0 10 20 30 40 50 60 70 80 90

Quality Q=target/background

t(min)

%uncorrected dose (uncorrected)

Figure 7: Figure of merit Q with estimated bounds.

Further work is being carried out to include the

effect of measurement noise, and applying the pro-

posed technique to complicated problems in biology

(including the presence of time-varying delays).

This work has been funded by MiCInn DPI2007-

66718-C04-02 and a ”Ram´on y Cajal” grant.

REFERENCES

Ait Rami, M., Helmke, U., Tadeo, F. Positive Observation

Problem For Linear Time-Lag Positive Systems IFAC

Workshop on Systems, Structure and Control, Foz de

Iguazu, Brazil, 2007.

Ait Rami, M., Helmke, U., Tadeo, F. Positive observation

problem for time-delays linear positive systems. IEEE

Mediterranean Control Conference, Greece, 2007.

Alamo, T., Bravo, J.M., Camacho, E.F., Guaranteed state

estimation by zonotopes, Automatica, 41(6): 1035-

1043, 2005.

Blake, G.M., Park-Holohan, S.-J., Fogelman, I., Quantita-

tive Studies of Bone in Postmenopausal Women Using

F-Fluoride and

99m

Tc-Methylene Diphosphonate. J

of Nuclear Medicine, 43:338-345.

Combastel, C.. A state bounding observer for uncertain non-

linear continuous-time systems based on zonotopes.

44th IEEE CDC, Seville, 2005.

Cook, G.J.R., Lodge, M.A., Blake, G.M., Marsden, Pl.K.,

Fogelman, I. Differences in skeletal kinetics between

vertebral and humeral bone measured by

F-Fluoride

positron emission tomography in postmenopausal

women. J Bone Mineralization Research 15:763-769,

2000.

Fogelman, I., Citrin, D.L., McKillop, J.H. et al., A clini-

cal comparison of Tc-99m HEDP and Tc-99m MDP

in the detection of bone metastases. J of Nuclear

Medicine 20: 98-101, 1979.

Gouze, J.L., Rapaport, A., Hadj-Sadok, Z.M.. Interval ob-

servers for uncertain biological systems. J of Ecologi-

cal Modelling, 133:4556, 2000.

Gover, R., Hwang, P.Y.C., Introduction to Random Signals

and Applied Kalman Filtering. John Wiley & Sons,

1997.

Hynne, F., Dano, S., Sorensen, P.G., Full-scale model of

glycolysis in Saccharomyces cerevisiae. Biophysical

Chemistry, 94: 12116, 2001.

Jacquez, J.A., Compartmental Analysis in Biology and

Medicine. Ann Arbor, MI: University of Michigan

Press, 1985.

Linninger, A.A., Xenos, M., Sweetman, B., Ponkshe, S.,

Guo, X., Penn, R. A mathematical model of blood,

cerebrospinal ﬂuid and brain dynamics. J of Mathe-

matical Biology, 59(6): 729-759, 2009.

Luenberger, D.G., An introduction to observers. IEEE

Trans. Aut. Control, 16: 596–602, 1966.

Luzyanina, T., Mrusek, S., Edwards, J.T., Roose, D., Ehl,

S., Bocharov, G., Computational analysis of CFSE

proliferation assay. J of Mathematical Biology 54(1):

57-89, 2007.

Makler, P.T., Charkes, N.D. Studies of Skeletal Tracer

Kinetics IV. Optimum Time Delay for Tc-99m(Sn)

Methylene Disphosphonate Bone Imaging, J of Nu-

clear Medicine, 21: 641-645, 1980.

Rapaport, A., Dochain, D., Interval observers for bio-

chemical processes with uncertain kinetics and inputs,

Mathematical Biosciences, 193(2) 235-253, 2005.

Rosenthall, L., Arzoumanian, A., Lisbona, R., et al., A lon-

gitudinal comparison of the kinetics of

99m

Tc-MDP

and

99m

Tc-EHDP in humans, Clin. Nucl. Med, 2:

232-234, 1997.

Subramanian, G., McAfee, J.G., Blair R.J. et al., An

evaluation of

99m

Tc-labeled phosphate compounds

as bone imaging agents, Radiopharmaceuticals, 319-

328, 1975.

Van Den Hof, J.M., Positive linear observers for linear

compartmental systems. SIAM J on Control and Op-

timization, 36: 590–608, 1998.

OBSERVATIONWITH BOUNDS OF BIOLOGICAL SYSTEMS - A Linear Programming Approach

235