
THE OBSERVABILITY PROBLEM IN TRAFFIC MODELS
An Algebraic Step by Step Method
Pilar Jim´enez, Santos S´anchez-Cambronero, Inmaculada Gallego and Ana Rivas
Department of Civil Engineering, University of Castilla La Mancha, 13071, Ciudad Real, Spain
Keywords:
Traffic model, Link flow estimation, OD flow estimation, Algebraic methods, Artificial intelligence.
Abstract:
This article deals with the problem of observability of traffic networks, understanding as such the problem of
identifying if a set of available flow measurements is sufficient to estimate the remaining flows in the network,
OD-pair or link flows. An algebraic method for solving the observability problems is given. Specifically, a
step by step procedure allowing updating the information once each item of information (OD-pair or link flow)
becomes available. The method is illustrated by its application to a simple network. The results show that the
proposed method provide useful information on which OD pair or link flows are informative on other OD pair
and link flows, and that the method is applicable to large networks due to its numerical robustness and stability.
1 INTRODUCTION
There are some situations in practice in which one
needs to know the state of a trafficnetwork by measur-
ing a subset of flows and, based on this information,
predicting other flows, which are not free to take ar-
bitrary values but must be subject to constraints, im-
posed by the networks topology, to be in agreement
with the measured flows. In this area, some Artificial
Intelligence techniques, such as Bayesian networks or
Neural networks, have been used (see (Castillo et al.,
2008c; Yin et al., 2002; Ledoux, (1997; Smith and
Demetsky, 1994), for example). However, before us-
ing these techniques it is important to discuss the ob-
servability problem, which consists of identifying if a
set of available (measured) flows is sufficient to cal-
culate other given subset of flows.
Observability analysis is a previous step to state
estimation. It addresses the question: do we have
enough measurements to estimate the state of a sys-
tem? Observability techniques are essential in many
fields of knowledge, and in particular in traffic predic-
tion.
Some examples of observability problems in traf-
fic networks are:
1. Determine if a subset of available traffic flows is
sufficient to obtain the values of another subset of
traffic flows.
2. Obtain a minimum subset of observations that al-
low the knowledge of other given subset of flows
or the observability of all flows in the network.
3. Identify observable flows, given a set of observed
flows (partial observability).
Though the problem of observability can be stated
in a general context, as done in (Castillo et al., 2007),
who discuss the problem of observability of linear
system of equations and inequalities, most of exist-
ing publications relate to particular fields (see, for ex-
ample, the survey provided by (Abur and Exp´osito,
2004), which includes applications to power sys-
tems).
Observability techniques can be classified as:
1. Algebraic. These techniques consider the al-
gebraic relations between the flows and operate
them algebraically to draw observability conclu-
sions (see (Monticelli and Wu, 1985a; Monticelli
and Wu, 1985b), (Monticelli, 2000), (Abur and
Exp´osito, 2004), (Gou and Abur, 2000; Gou and
Abur, 2001), (Castillo et al., 2005), (Castillo et
al., 2006), (Castillo et al., 2008a), (Castillo et al.,
2008b)).
2. Topological. These techniques consider only
topological and/or qualitative relations be-
tween flows to derive observability results (see
(Clements and Wollenberg, 1975); (Krumpholz
et al., 1980), (Nucera and Gilles, 1991) and
(Castillo et al., 2007; Castillo et al., 2008b)).
Since all these techniques are based on the math-
ematical properties of the systems of equations and
560
Jiménez P., Sánchez-Cambronero S., Gallego I. and Rivas A. (2010).
THE OBSERVABILITY PROBLEM IN TRAFFIC MODELS - An Algebraic Step by Step Method.
In Proceedings of the 2nd International Conference on Agents and Artificial Intelligence - Artificial Intelligence, pages 560-567
DOI: 10.5220/0002717805600567
Copyright
c
SciTePress

have the same structure for traffic problems, these ap-
proaches, which have already been applied to “phys-
ical” networks, are equally applicable to traffic net-
works.
This paper is focused on algebraic methods, which
can be used with two aims in mind: (a) obtaining the
exact algebraic relation among different flows, such
that some can be calculated when other are known,
and (b) obtain observability information, that is, de-
termine which flows can and which flows cannot be
calculated when a subset of flows is known, but with-
out seeking the corresponding formulas which allow
us the calculations. The second aim is simpler and
requires less effort than the first one.
This paper deals with observability problems, as-
suming that the matrix relating link and OD flows is
given. However, though the solution of the system of
equations implied by OD-link relations is clearly de-
pendent on the particular selection of the choice prob-
abilities or proportions of the users selecting different
paths, the observability problem is not in general. Of
course, there are many especial cases in which some
linear equations can become linear combinations of
other, but what we are really interested in is in struc-
tural linear dependencies and not accidental depen-
dencies. Thus, fixing the probabilities (unless they
are fixed to zero values) is not a problem. In fact, they
should be fixed at random with the aim of avoiding ac-
cidental dependencies (with zero probability in prac-
tice). Another different matter is to fix some proba-
bilities to zero or not zero. This means incorporating
or deleting paths, and then, the observability problem
is clearly dependent on these selections.
Note that the technique developed is applicable
not only for observingtotal link flows, but also for dis-
aggregated link flows, by origin, destinations, or any
type of disaggregation as that associated with plate
scanning. However, for the sake of simplicity we il-
lustrate the method with total link flows.
This paper is organized as follows. In section 2
the observability problem is stated and the algebraic
method is given. Section 3 illustrates the proposed
method by their application to a simple network. Fi-
nally, in Section 4 some conclusions are given.
2 THE OBSERVABILITY
PROBLEM
Consider a traffic network (N , A ) where N is the set
of nodes and A is the set of links. Let v
a
be the flow of
link a, p
ik
the probability of a user to choose path k of
the OD-pair i, t
i
the OD-pair flow i, δ
i
ak
the incidence
matrix, that is, δ
i
ak
= 1 if link a belongs to path k of
OD-pair i, and 0, otherwise.
Then, for compatibility of OD-pair and link flows,
i.e., for the conservation law to be satisfied, one must
have:
v
a
=
∑
i
∑
k
p
ik
δ
i
ak
!
t
i
=
∑
i
f
ai
t
i
, (1)
where F is a matrix with elements f
ai
defined as
f
ai
=
∑
k
p
ik
δ
i
ak
;
∑
k
p
ik
= 1; ∀i. (2)
The system of equations (1) in matrix form becomes
V = FT, (3)
where V and T are the column matrices of link and
OD-pair flows with dimensions m × 1 and n × 1, re-
spectively.
It is important to note that given the OD flows t
i
,
Equation (3) allows us to calculate the link flows v
a
.
Thus, given the topology of the network and the OD
path flows, the OD flows are the minimum number of
data items needed to determine the remaining flows
of the network. In fact, enumerating paths can be
avoided if the matrix F, which gives the proportions
of OD flows travelling through each link, is known.
However, since OD flows are not normally known,
each of them needs to be replaced by link flows that
are practically observable. As we will see, the alge-
braic approach proceeds by replacing the OD flows
with the observed links, until all of them have been
replaced.
Therefore, it is assumed that a subset T
1
of T and
a subset V
1
of V are observed (known) and the com-
plementary subsets T
0
of T and V
0
of V are not.
Then, the system (3) can be partitioned as
V
0
− − −
V
1
!
=
F
00
| F
01
− − − + −− −
F
10
| F
11
!
T
0
− − −
T
1
!
, (4)
In order to join (write together) the unknown flow
variables T
0
and V
0
, the system (4) can be written
in the alternative equivalent form
D =
−F
01
T
1
− − − − −
−F
11
T
1
+ V
1
= Bz =
F
00
| −I
p
− − − + − − −
F
10
| 0
T
0
− − − − −
V
0
,
(5)
a system where the unknowns appear on the right
hand side and the observations on its left hand side.
The coefficient matrix is B, the independent term col-
umn matrix is D and z contains the unknown flows T
0
and V
0
.
We finally note that for illustrative purposes and
for the sake of facilitating the understanding of this
example, the OD-pair and link flows have been dis-
tinguished as two different items, but from a mathe-
matical point of view they are undistinguishable. In
other words, the data and the unknown sets can con-
tain any subset of variables.
THE OBSERVABILITY PROBLEM IN TRAFFIC MODELS - An Algebraic Step by Step Method
561

2.1 The Algebraic Approach: A
Step-by-step Procedure
The step-by-step procedure allows us to discover what
happens, in terms of observability, as some new items
of information (OD-pair or link flows) become avail-
able.
The rationale for the algorithm below is basically
to express the observable flows in terms of the actu-
ally observed flows. That is, to transfer “columns to
rows” and vice versa in matrix F. If all variables can
be expressed as linear combinations of measurements,
the network is observable; otherwise, it is not. The
actual operations are based on the orthogonal trans-
formation algorithm reported in (Castillo et al., 2000;
Castillo et al., 2002). The proposed algorithm pro-
vides two sets and one matrix of interest:
1. Set C of cardinality n, whose elements are c
j
, con-
tains the list of a minimum set of required mea-
surements to attain observability of all variables.
These measurements are denominated essential
measurements or basic measurements.
2. Set B of cardinality m, whose elements are b
i
,
contains the list of redundant measurements for
observability purposes, that is, even if the mea-
surements are lost, the network remains observ-
able.
3. Matrix F
1
of dimension m× n contains the coeffi-
cients of the linear combinations of the redundant
measurements in terms of the required (essential)
ones.
Algorithm 1 (Basic observability procedure).
INPUT. The set of links A , the set of OD-pairs,
two disjoint subsets B and C of the set H of all flows
(OD-pair and link flows) such that H = B ∪ C , B ∩
C =
/
0 and |C | = n, an initial matrix F giving the flows
in B in terms of the flows in C .
OUTPUT. A transformed matrix F
∗
associated
with the transformed
¯
B and
¯
C sets.
Step 1: Choose a pivot. Choose an unobservable el-
ement in B , that is, a row i of matrix F that we called
α, and an element in C , that is a column j of the same
matrix, called β, such that the corresponding value
f
αβ
6= 0, and go to Step 2. If such an element f
αβ
is
null, stop the process informing on the impossibility
of exchanging the supplied elements b
α
and c
β
.
1
Matrix F can be easily obtained from the network
topology. For example, it can be the matrix F in (3) or any
other resulting after manipulation of this one by exchanging
the variables in B and C .
Step 2: Pivoting. Perform the pivoting process, that
is, calculate the transformed matrix F
∗
using the fol-
lowing transformation, being α and β the i row and j
column, respectively, chosen for pivoting in Step 1,
f
∗
ij
=
f
ij
−
f
αj
f
αβ
f
iβ
if i 6= α; j 6= β
−
f
αj
f
αβ
if i = α; j 6= β
f
iβ
f
αβ
if i 6= α; j = β
1
f
αβ
if i = α; j = β
(6)
Next, exchange the flow c
β
in terms of the flow b
α
and all other flows in C at this stage. In other words,
incorporate the flow in position α of B into position β
of list C, and the flow in position β of C into position
α of list B.
Once replaced c
β
in all equations associated with
the system
B = FC,
we obtain the new matrix F
∗
such that
B
∗
= F
∗
C
∗
,
where the asterisk refers to the new situation, i.e. after
the interchange of b
α
and c
β
has been done.
Note that the systems of equations B = FC and
B
∗
= F
∗
C
∗
are equivalent in the sense that they have
the same solutions.
Step 3: Update the list of essential and redundant
flows. Return matrix F
∗
and the updated flow subsets
B
∗
and C
∗
. If a non-boldfaced flow in B (row of F
∗
)
has null coefficients in all its columns associated with
non-observable basic flows (columns of F
∗
), the flow
is observable, and then its name is boldfaced, that is,
added to the set of observable flows.
Since it appears to be more convenient and infor-
mative to update the flow knowledge as soon as each
unit of information is obtained, an algorithm for this
step-by-step process is given below. It uses Algorithm
1 as its main tool.
Algorithm 2 (Observability updating procedure).
INPUT. A list D of flows to be observed, the
initial matrix F, and a partition B and C of all the
flow variables H (OD-pair and link flows) such that
H = B ∪ C , B ∩ C =
/
0 and |C | = n.
OUTPUT. The updated matrix F
∗
and sets B
∗
and C
∗
, together with the sets B and C of all flows
that become known in B and C , respectively, due to
the observed flows in each step.
ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence
562

Step 0: Initialization step. Initialize the sets B and
C of known flows in B and C , respectively, to empty
sets.
Repeat the following steps for each flow d
r
in the
list D .
Step 1: Update observability matrix. If the flow d
r
is already in set C , i.e. d
r
coincides with some c
β
∈ C ,
simply add d
r
to list C . Otherwise, it must coincide
with some b
α
∈ B , and then use Algorithm 1 to
incorporate the flow variable d
r
≡ b
α
to set C . To this
end, select a flow c
β
of C not in C to be exchanged
with d
r
. If this is not possible because there is no
non-null element f
αj
, inform on this impossibility
of observing d
r
(it must already have a fixed value,
which can be calculated in terms of already observed
flows) increase r in one unit and continue in Step 1.
Otherwise, update matrix F to F
∗
, exchange flows c
β
and d
r
in sets B and C , respectively, using Algorithm
1 and add d
r
to list C .
Step 2: Identify all known flows in set B . Find the
known flows b
k
∈ B , i.e. the rows of F such that the
f
kj
are null for all j associated with the unknown
flows in C , and add them to set B .
Step 3: Return observability information. Return
matrix F
∗
, the sets B
∗
and C
∗
, and the subsets of
known flows B and C , increase r in one unit and con-
tinue in Step 1.
Both algorithms 1 and 2 return matrices F
∗
, which
give the symbolic relation between the flows in B and
those in C , that is, the linear formulas that permit the
flows in B to be written in terms of those in C . Note
that once calculated, they can be used many times (for
observations taken at different days, hours, etc.).
Note that the technique in Algorithms 1 and 2 does
not require the actual values of the observed flows.
This is an important advantage from a practical point
of view because one is not subject to observation er-
rors that in quite a few cases can and certainly do lead
to the incompatibility of the system of equations (3).
Since this method works using algebraic opera-
tions with real numbers, it is subject to rounding er-
rors. In particular, testing for zero flows must be re-
placed by testing for small numbers, which can give
numerical problems for large networks.
With respect to use the second algorithm with
a given list D of observable flows, it is convenient
to study the rank associated with the rows of D , to
avoid observing redundant flows, that is, a set of flows
which contains the same information as a proper sub-
set of it. This check permits the unnecessary observa-
tions, i.e., those observations that are linear combina-
tions of other observations, to be eliminated.
2.2 Computational Issues
In this section we deal with some computational is-
sues.
Since the proposed method is a pivoting process
analogous to the Gauss elimination, all the gained ex-
perience for Gauss methods is applicable to the pro-
posed method. This implies that it is applicable to
very large networks.
For some particular cases of the choice probabil-
ities and network topologies, the system can become
ill-conditioned, and then, the standard methods used
to solve this problem can be applied. In particular one
can use the different well known partial and complete
pivot strategies, which are very useful.
The complexity of algorithm 2 is similar to the
complexity of inverting a matrix. If one has n essen-
tial variables, the number of operations required for
obtaining a minimum set of observed links for observ-
ability of the whole system is (3n−1)n
2
, which gives
a clear idea of how the size of the problem affects the
computational time.
3 EXAMPLE OF APPLICATION
In this section we illustrate the proposedmethod by its
application to a simple network in order to be able to
show the results in form of tables of reasonable size.
Though this method was tested using other networks,
as the Nguyen-Dupuis network (13 nodes, 38 links, 8
OD pairs, 50 routes), and the real Ciudad Real net-
work (102 nodes, 218 links, 72 OD pairs, 179 routes),
for example, and similar results were obtained. Since
the algebraic techniques used are very well known
from the point of view of their numerical robustness
and stability, it can be said that they behave very well
for very large networks.
The simple network consists of 9 nodes and 18
links, as shown in Figure 1. We use an example of
bidirectional flow, i.e., we assume the existence of
symmetric links, i.e. any pair of nodes i and j is con-
nected in both directions by links ℓ
ij
and ℓ
ji
, respec-
tively.
We have assumed the following OD-pairs flows
(elements of the matrix T):
{t
1
,t
2
,t
3
,t
4
,t
5
,t
6
} ≡ {t
14
,t
24
,t
34
,t
41
,t
42
,t
43
},
where the subindices refer to the OD-pair or the node
numbers, respectively, and the paths (given in terms
THE OBSERVABILITY PROBLEM IN TRAFFIC MODELS - An Algebraic Step by Step Method
563
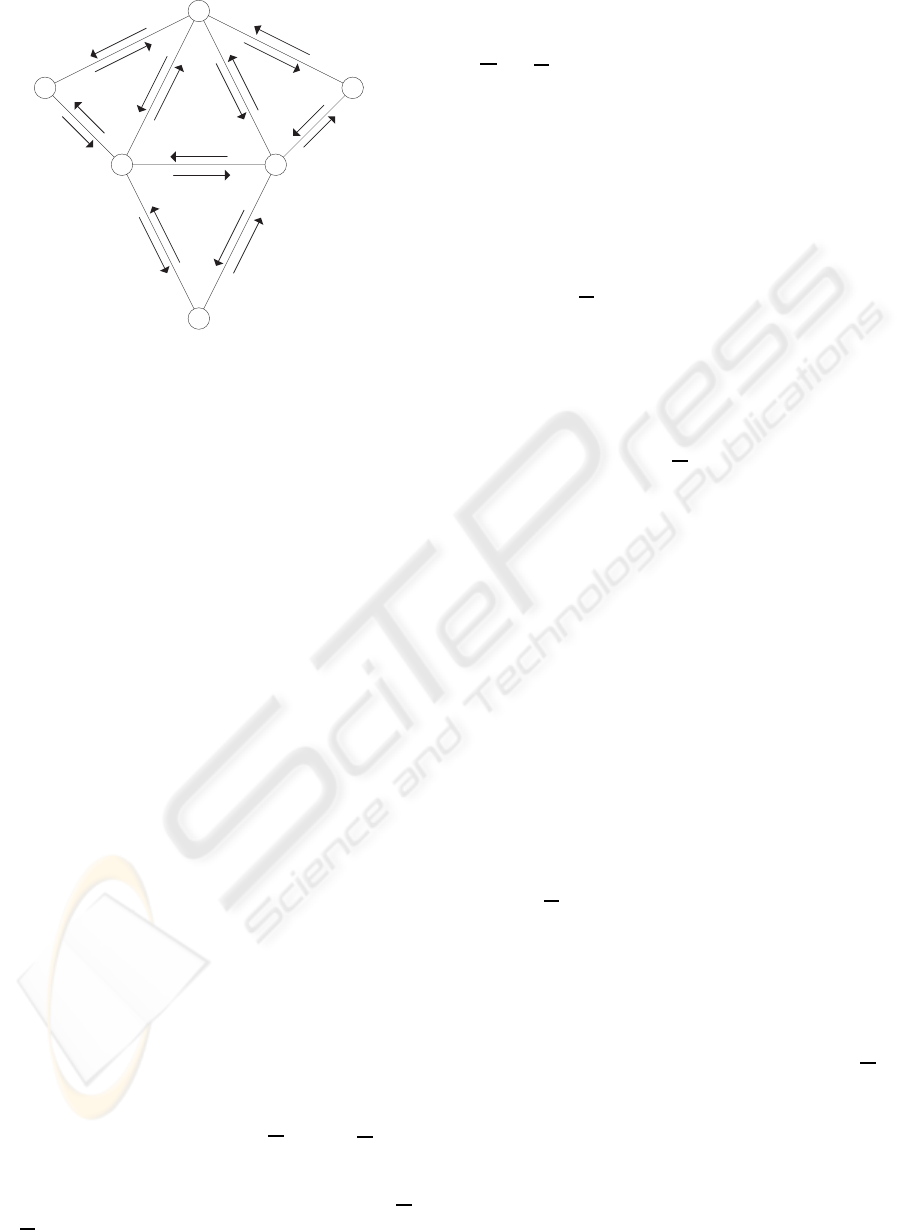
1
4
1
2
3
4
5
6
7
8
9
5
6
2
3
10
12
11
13
16
14
17
15
18
Figure 1: The simple network, showing the nodes and links.
of nodes):
OD-pair 1− 4 : {1, 2,5, 4}, {1,2, 5,6, 4}, {1,5, 4},
{1, 5,6, 4}, {1,6, 4}, {1,6, 5,4},
{1, 3,6, 4}, {1,3, 6,5, 4},
OD-pair 2− 4 : {2, 5,4}, {2, 5,6, 4},
OD-pair 3− 4 : {3, 6,5, 4}, { 3,6, 4},
OD-pair 4− 1 : {4, 5,2, 1}, { 4,6, 5,2, 1}, {4,5, 1},
{4, 6,5, 1}, {4,6, 1}, {4,5, 6,1},
{4, 6,3, 1}, {4,5, 6,3, 1},
OD-pair 4− 2 : {4, 5,2}, {4, 6,5, 2},
OD-pair 4− 3 : {4, 5,6, 3}, { 4,6, 3}.
To illustrate the step-by-step method we explain
our input data and give a detailed explanation of the
different steps in Algorithm 2 below.
Example 1 (The step-by-step approach) .
INPUT. It consists of the following list D of flows
to be observed (only link flows are observed in this
example):
D ≡ {v
1
,v
8
,v
10
,v
11
,v
12
,v
15
},
the initial matrix F, which has been obtained using
(1), and is given in Table 1, iteration 0, and as
partition of the flow variables H we take B as the
set of link flows, and C as the set of OD-pair flows,
respectively.
Step 0: Initialization step. We initialize the sets of
known flows to empty sets, that is, B =
/
0 and C =
/
0.
We show the initial sets B and C and their updated
versions B
∗
and C
∗
in the first rows and columns, re-
spectively, of the tables, and we distinguish the sets B
and C with boldfaced letters.
With all this, we have the initial observability
information in Table 1, iteration 0. Note that in this
and the following tables, the matrix F and the sets B ,
C , B and C are shown.
Next, we repeat the following steps for each flow
d
r
in the list D , starting with flow v
1
.
Step 1: Update observability matrix. Since the
flow v
1
is not in set C but is in set B , Algorithm 1
is used to incorporate the flow variable v
1
to set C.
To this end, we select the flow c
β
≡ t
1
of C to be
exchanged with v
1
, and update matrix F to F
∗
and
add v
1
to list C (boldfaced) (see the right part of
Table 1).
Step 2: Identify all known flows in set B . At this
stage, there are known flows b
k
∈ B , i.e. there are
rows of matrix F with null values in the columns of
unknown flows in C , {t
2
,t
3
,t
4
,t
5
,t
6
}. So, the flows
{t
1
,v
3
,v
5
,v
7
} are added to B .
Step 3: Return observability information. We
produce this information in the right part of Table 1.
Since repeating all the steps for all the iterations
would be too reiterative and space consuming, we
assume that we are at the beginning of iteration 4 (see
Table 3), i.e., when we will observe v
12
, and continue
with Steps 1 to 3, as follows.
Step 1: Update observability matrix. Since the
flow v
12
is not in set C but is in set B , Algorithm
1 is used to incorporate the flow variable v
12
to set
C. To this end, we select the flow c
β
≡ t
2
of C to be
exchanged with v
12
. Note that this is not the only
option, because there are other non-null f
αj
values
associated with the unobserved flows in C , such as
v
14
or v
15
. Then, we update matrix F to F
∗
and add
v
12
to list C (we boldface it, as shown in Table 3),
iteration 5.
Step 2: Identify all known flows in set B . At this
stage, there are flows b
k
∈ B which become known,
i.e. there are rows of the matrix F with null values in
the column of t
3
, the only unknown flow in C . In this
iteration, v
14
is the only new known flow added to B .
Step 3: Return observability information. We
return the information in Table 3, iteration 5.
Finally, in the next iteration all the flows become
known (see that in Table 4 all the flows are boldfaced).
Note also that the coefficients in this table permit
ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence
564
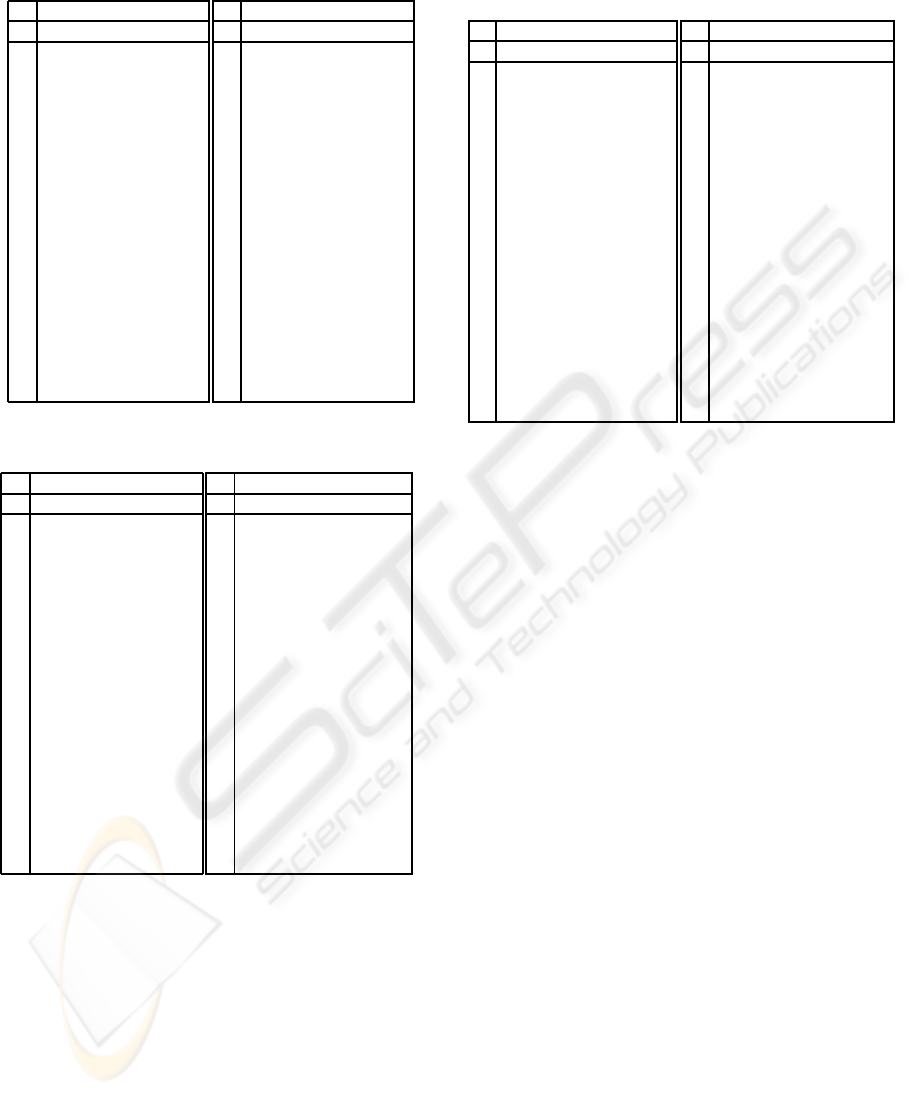
Table 1: Initial F matrix and F after observing {v
1
}.
Iteration 0
t
1
t
2
t
3
t
4
t
5
t
6
v
1
0.3 0.0 0.0 0.0 0.0 0.0
v
2
0.0 0.0 0.0 0.3 0.0 0.0
v
3
0.3 0.0 0.0 0.0 0.0 0.0
v
4
0.0 0.0 0.0 0.3 0.0 0.0
v
5
0.3 0.0 0.0 0.0 0.0 0.0
v
6
0.0 0.0 0.0 0.3 0.0 0.0
v
7
0.3 0.0 0.0 0.0 0.0 0.0
v
8
0.0 0.0 0.0 0.3 0.0 0.0
v
9
0.3 0.0 0.7 0.0 0.0 0.0
v
10
0.0 0.0 0.0 0.3 0.0 1.0
v
11
0.3 0.0 0.3 0.3 0.5 0.0
v
12
0.3 0.3 0.0 0.3 0.0 0.5
v
13
0.0 0.0 0.0 0.3 1.0 0.0
v
14
0.3 0.7 0.0 0.0 0.0 0.0
v
15
0.5 0.3 0.3 0.0 0.0 0.0
v
16
0.0 0.0 0.0 0.5 0.5 0.5
v
17
0.5 0.3 0.3 0.0 0.0 0.0
v
18
0.0 0.0 0.0 0.5 0.5 0.5
Iteration 1
v
1
t
2
t
3
t
4
t
5
t
6
t
1
4.0 0.0 0.0 0.0 0.0 0.0
v
2
0.0 0.0 0.0 0.3 0.0 0.0
v
3
1.0 0.0 0.0 0.0 0.0 0.0
v
4
0.0 0.0 0.0 0.3 0.0 0.0
v
5
1.0 0.0 0.0 0.0 0.0 0.0
v
6
0.0 0.0 0.0 0.3 0.0 0.0
v
7
1.0 0.0 0.0 0.0 0.0 0.0
v
8
0.0 0.0 0.0 0.3 0.0 0.0
v
9
1.0 0.0 0.7 0.0 0.0 0.0
v
10
0.0 0.0 0.0 0.3 0.0 1.0
v
11
1.0 0.0 0.3 0.3 0.5 0.0
v
12
1.0 0.3 0.0 0.3 0.0 0.5
v
13
0.0 0.0 0.0 0.3 1.0 0.0
v
14
1.0 0.7 0.0 0.0 0.0 0.0
v
15
2.0 0.3 0.3 0.0 0.0 0.0
v
16
0.0 0.0 0.0 0.5 0.5 0.5
v
17
2.0 0.3 0.3 0.0 0.0 0.0
v
18
0.0 0.0 0.0 0.5 0.5 0.5
Table 2: F after observing {v
1
,v
8
} and {v
1
,v
8
,v
10
}.
Iteration 2
v
1
t
2
t
3
v
8
t
5
t
6
t
1
4.0 0.0 0.0 0.0 0.0 0.0
v
2
0.0 0.0 0.0 1.0 0.0 0.0
v
3
1.0 0.0 0.0 0.0 0.0 0.0
v
4
0.0 0.0 0.0 1.0 0.0 0.0
v
5
1.0 0.0 0.0 0.0 0.0 0.0
v
6
0.0 0.0 0.0 1.0 0.0 0.0
v
7
1.0 0.0 0.0 0.0 0.0 0.0
t
4
0.0 0.0 0.0 4.0 0.0 0.0
v
9
1.0 0.0 0.7 0.0 0.0 0.0
v
10
0.0 0.0 0.0 1.0 0.0 1.0
v
11
1.0 0.0 0.3 1.0 0.5 0.0
v
12
1.0 0.3 0.0 1.0 0.0 0.5
v
13
0.0 0.0 0.0 1.0 1.0 0.0
v
14
1.0 0.7 0.0 0.0 0.0 0.0
v
15
2.0 0.3 0.3 0.0 0.0 0.0
v
16
0.0 0.0 0.0 2.0 0.5 0.5
v
17
2.0 0.3 0.3 0.0 0.0 0.0
v
18
0.0 0.0 0.0 2.0 0.5 0.5
Iteration 3
v
1
t
2
t
3
v
8
t
5
v
10
t
1
4.0 0.0 0.0 0.0 0.0 0.0
v
2
0.0 0.0 0.0 1.0 0.0 0.0
v
3
1.0 0.0 0.0 0.0 0.0 0.0
v
4
0.0 0.0 0.0 1.0 0.0 0.0
v
5
1.0 0.0 0.0 0.0 0.0 0.0
v
6
0.0 0.0 0.0 1.0 0.0 0.0
v
7
1.0 0.0 0.0 0.0 0.0 0.0
t
4
0.0 0.0 0.0 4.0 0.0 0.0
v
9
1.0 0.0 0.7 0.0 0.0 0.0
t
6
0.0 0.0 0.0 -1.0 0.0 1.0
v
11
1.0 0.0 0.3 1.0 0.5 0.0
v
12
1.0 0.3 0.0 0.5 0.0 0.5
v
13
0.0 0.0 0.0 1.0 1.0 0.0
v
14
1.0 0.7 0.0 0.0 0.0 0.0
v
15
2.0 0.3 0.3 0.0 0.0 0.0
v
16
0.0 0.0 0.0 1.5 0.5 0.5
v
17
2.0 0.3 0.3 0.0 0.0 0.0
v
18
0.0 0.0 0.0 1.5 0.5 0.5
obtaining all the flows of B in terms of the observed
flows, that now are all the flows in C :
t
1
= 4v
1
v
2
= v
8
.. . . .. . . . .. . .. . . . . ... .. .
v
9
= −v
1
−2v
12
2v
15
v
8
v
10
t
6
= −v
8
v
10
.. . . .. . . . .. . .. . . . . ... .. .
v
17
= v
15
v
18
= v
12
−v
15
v
11
Next, we illustrate the general problems stated in the
introduction with some particular cases.
Table 3: F after observing {v
1
,v
8
,v
10
,v
11
} and
{v
1
,v
8
,v
10
,v
11
,v
12
}.
Iteration 4
v
1
t
2
t
3
v
8
v
11
v
10
t
1
4.0 0.0 0.0 0.0 0.0 0.0
v
2
0.0 0.0 0.0 1.0 0.0 0.0
v
3
1.0 0.0 0.0 0.0 0.0 0.0
v
4
0.0 0.0 0.0 1.0 0.0 0.0
v
5
1.0 0.0 0.0 0.0 0.0 0.0
v
6
0.0 0.0 0.0 1.0 0.0 0.0
v
7
1.0 0.0 0.0 0.0 0.0 0.0
t
4
0.0 0.0 0.0 4.0 0.0 0.0
v
9
1.0 0.0 0.7 0.0 0.0 0.0
t
6
0.0 0.0 0.0 -1.0 0.0 1.0
t
5
-2.0 0.0 -0.7 -2.0 2.0 0.0
v
12
1.0 0.3 0.0 0.5 0.0 0.5
v
13
-2.0 0.0 -0.7 -1.0 2.0 0.0
v
14
1.0 0.7 0.0 0.0 0.0 0.0
v
15
2.0 0.3 0.3 0.0 0.0 0.0
v
16
-1.0 0.0 -0.3 0.5 1.0 0.5
v
17
2.0 0.3 0.3 0.0 0.0 0.0
v
18
-1.0 0.0 -0.3 0.5 1.0 0.5
Iteration 5
v
1
v
12
t
3
v
8
v
11
v
10
t
1
4.0 0.0 0.0 0.0 0.0 0.0
v
2
0.0 0.0 0.0 1.0 0.0 0.0
v
3
1.0 0.0 0.0 0.0 0.0 0.0
v
4
0.0 0.0 0.0 1.0 0.0 0.0
v
5
1.0 0.0 0.0 0.0 0.0 0.0
v
6
0.0 0.0 0.0 1.0 0.0 0.0
v
7
1.0 0.0 0.0 0.0 0.0 0.0
t
4
0.0 0.0 0.0 4.0 0.0 0.0
v
9
1.0 0.0 0.7 0.0 0.0 0.0
t
6
0.0 0.0 0.0 -1.0 0.0 1.0
t
5
-2.0 0.0 -0.7 -2.0 2.0 0.0
t
2
-3.0 3.0 0.0 -1.5 0.0 -1.5
v
13
-2.0 0.0 -0.7 -1.0 2.0 0.0
v
14
-1.0 2.0 0.0 -1.0 0.0 -1.0
v
15
1.0 1.0 0.3 -0.5 0.0 -0.5
v
16
-1.0 0.0 -0.3 0.5 1.0 0.5
v
17
1.0 1.0 0.3 -0.5 0.0 -0.5
v
18
-1.0 0.0 -0.3 0.5 1.0 0.5
Problem 1. Determine if the subset of link flows
B ≡ {v
1
,v
8
} is sufficient to determine the subset
of traffic flows G ≡ {v
2
,v
3
,v
4
,v
5
,v
6
,v
7
}.
Solution. The answer to this problem is positive, be-
cause supplying the given set B as the input list to
Algorithm 2, it returns what it is in Table 2, iter-
ation 2, where we can see that all the flows in the
given set G are boldfaced, i.e. the flows in G are
observable.
Moreover, if we compare these results with Fig-
ure 1, we are able to deduce that the firsts eight
links of the network (upper area) are lineal com-
binations. So, any pair of links of this set
{v
1
,v
2
,v
3
,v
4
,v
5
,v
6
,v
7
,v
8
} allows us to know the
flow of all these links.
Problem 2. Determine a minimum set of observa-
tions (OD-pair and/or link flows) that allow ob-
servability of the network.
Solution. Since the rank of matrix F in Table 3 is
n = 6, then, the minimum subset must contain
6 flows. Thus, after applying Algorithm 2 with
D ≡ {v
1
,v
8
,v
10
,v
11
,v
12
,v
18
} we obtain Iteration
6, Table 4, where all observable flows are bold-
faced, i.e., those whose coefficients of unobserved
essential variables are null (this means that the lin-
ear combinations can be calculated, because all
nonnull terms are known).
Problem 3. Identify observable flows, given the set
of observed flows {v
1
,v
8
,v
10
,v
11
}.
Solution. In Iteration 4 of Table 3, after incorpo-
rating all observed flows, it can be seen that
t
1
,t
4
,t
6
,v
2
,v
3
,v
4
,v
5
,v
6
and v
7
have a zero in the
THE OBSERVABILITY PROBLEM IN TRAFFIC MODELS - An Algebraic Step by Step Method
565
Table 4: F after observing {v
1
,v
8
,v
10
,v
11
,v
12
,v
18
}.
Iteration 6
v
1
v
12
v
15
v
8
v
11
v
10
t
1
4.0 0.0 0.0 0.0 0.0 0.0
v
2
0.0 0.0 0.0 1.0 0.0 0.0
v
3
1.0 0.0 0.0 0.0 0.0 0.0
v
4
0.0 0.0 0.0 1.0 0.0 0.0
v
5
1.0 0.0 0.0 0.0 0.0 0.0
v
6
0.0 0.0 0.0 1.0 0.0 0.0
v
7
1.0 0.0 0.0 0.0 0.0 0.0
t
4
0.0 0.0 0.0 4.0 0.0 0.0
v
9
-1.0 -2.0 2.0 1.0 0.0 1.0
t
6
0.0 0.0 0.0 -1.0 0.0 1.0
t
5
0.0 2.0 -2.0 -3.0 2.0 -1.0
t
2
-3.0 3.0 0.0 -1.5 0.0 -1.5
v
13
0.0 2.0 -2.0 -2.0 2.0 -1.0
v
14
-1.0 2.0 0.0 -1.0 0.0 -1.0
t
3
-3.0 -3.0 3.0 1.5 0.0 1.5
v
16
0.0 1.0 -1.0 0.0 1.0 0.0
v
17
0.0 0.0 1.0 0.0 0.0 0.0
v
18
0.0 1.0 -1.0 0.0 1.0 0.0
column positions of t
2
and t
3
, which are the only
unknown OD flows in set C .
4 CONCLUSIONS
The problem of exact observability of traffic flows can
be dealt with in a simple form even for large net-
works. To solve this problem an algebraic step-by-
step method is given. This method allows determining
the set of observable flows and permits updating the
observability information every time we have a new
item of information, so that a detailed observability
analysis can be done at each step of the process.
The illustration of the proposed methodology us-
ing a simple network shows that the proposed method
is efficient and practically valid.
Finally, some suggestions for future work are the
application of topological techniques to traffic net-
works, and developing an alternative method sharing
the advantages of both observability techniques alge-
braic and topological.
ACKNOWLEDGEMENTS
The authors are indebted to the Spanish Ministry of
Science and Technology (Project BIA2005-07802-
C02-01) and to the Council of Education and Science
of Castilla-La Mancha (Project A06-016) for partial
support of this work.
REFERENCES
Abur, A. and G´omez Exp´osito, A. (2004). Power System
State Estimation-Theory and Implementations. Mar-
cel Dekker, Inc., New York.
Castillo, E., Cobo, A., Jubete, F., Pruneda, R., and
Castillo, C. (2000). An orthogonally based pivot-
ing transformation of matrices and some applications.
SIAM Journal on Matrix analysis and Applications,
22:666681.
Castillo, E., Conejo, A., Men´endez, J. M., and Jimenez, P.
(2008a). The observability problem in traffic network
models. Computer Aided Civil and Infrastructure En-
gineering, 23. Special issue on traffic computational
models.:208222.
Castillo, E., Conejo, A., Pruneda, E., and Solares, C.
(2005). State estimation observability based on the
null space of the measurement jacobian matrix. IEEE
Transactions on Power Systems, 20:16561658.
Castillo, E., Conejo, A., Pruneda, E., and Solares, C.
(2006). Observability analysis in state estimation.
IEEE Transactions on Power Systems, 21:877886.
Castillo, E., Conejo, A., Pruneda, E., and Solares, C.
(2007). Observability in linear systems of equations
and inequalities. applications. Computers and Opera-
tion Research, 34:17081720.
Castillo, E., Jim´enez, P., Menendez, J. M., and Conejo, A.
(2008b). The observability problem in traffic models:
algebraic and topological methods. IEEE Transactions
on Intelligent Transportation System, 9:2:275287.
Castillo, E., Jubete, F., Pruneda, R., and Solares, C. (2002).
Obtaining simultaneous solutions of linear subsys-
tems of equations and inequalities. Linear Algebra
and its Applications., 346:131154.
Castillo, E., Men´endez, J. M., and S´anchez-Cambronero, S.
(2008c). Predicting traffic flow using Bayesian net-
works. Transportation Research B, 42:5:482509.
Clements, K. A. and Wollenberg, B. F. (1975). An algo-
rithm for observability determination in power sys-
tem state estimation. IEEE PES Summer Meeting,
A75:447449.
Gou, B. and Abur, A. (2000). A direct numerical method for
observability analysis. IEEE Transactions on Power
Systems, 15:2:625630.
Gou, B. and Abur, A. (2001). An improved measurement
placement algorithm for network observability. IEEE
Transactions on Power Systems, 16:4:819824.
Krumpholz, G., Clements, K., and Davis, P. (1980). Power
system observability - a practical algorithm using net-
work topology. IEEE Transactions on Power Appara-
tus Systems, 99:4:15341542.
Ledoux, C. (1997). An urban traffic flow model inte-
grating neural networks. Transportation Research C,
5:5:287300.
Monticelli, A. (2000). Electric power system state estima-
tion. Proceedings of the IEEE, 88:2:262282.
ICAART 2010 - 2nd International Conference on Agents and Artificial Intelligence
566

Monticelli, A. and Wu, F. (1985a). Network observability -
identification of observable islands and measurement
placement. IEEE Transactions on Power Apparatus
Systems, 104:5:10351041.
Monticelli, A. and Wu, F. (1985b). Network observability
- theory. IEEE Transactions on Power Apparatus Sys-
tems, 104:5:10421048.
Nucera, R. and Gilles, M. (1991). Observability analysis:
A new topological algorithm. IEEE Transactions on
Power Systems, 6:2:466475.
Smith, B. L. and Demetsky, M. J. (1994). Short-term traf-
fic flow prediction: Neural network approach. Trans-
portation Research Record, 1453:98104.
Yin, H., Wong, S. C., Xu, J., and Wong, C. K. (2002). Urban
traffic flow prediction using a fuzzy-neural approach.
Transportation Research C, 10:2:8598.
THE OBSERVABILITY PROBLEM IN TRAFFIC MODELS - An Algebraic Step by Step Method
567
