HOLY-II: IMPROVED HIERARCHICALLY ORGANIZED

LAYOUT FOR VISUALIZATION OF BIOCHEMICAL COMPLEX

PATHWAYS

Jyh-Jong Tsay, Bo-Liang Wu and Guo-Gen Huang

Dept. of Computer Science & Information Engineering, National Chung-Cheng University, Taiwan, R.O.C.

Keywords: Pathway layout, Forced-directed layout, Hierarchical layout, Pathway visualization.

Abstract: Many complex pathways are described as hierarchical structures in which a pathway is recursively

partitioned into several sub-pathways, and organized hierarchically as a tree. The hierarchical structure

provides a natural way to visualize the global structure of a complex pathway. Recently, a hierarchically

organized layout algorithm HOLY which takes the advantages of the hierarchical structures inherent in

complex pathways has been proposed. In this paper, we present a new layout algorithm HOLY-II which

follows the basic principle of HOLY, but improves HOLY by introducing a new algorithm for joining

layouts, one of the crucial tasks in HOLY. Experiment shows that HOLY-II is able to produce layouts

which clearly render both the global structures and the local structures of complex pathways, and gives

better visualization for many examples from MetaCyc, CADLIVE and HOLY.

1 INTRODUCTION

Automatic drawing and visualization of pathways

plays an important role in understanding biological

systems. Recently, several pathway editors (Trost et

al., 2003; Brandenburg et al., 2004; Salamonsen et

al., 2004) have been developed. Such editors provide

graphical interfaces, and graphical components that

match pathway components. However, pathway data

is increasing very rapidly, and updated frequently.

That makes drawing and maintaining of pathway

data tedious and time-consuming, even we use

graphical editors. A solution to the problem is to

develop software tools that can automatically layout

and visualize pathways.

One of the main problems in automatic

pathway drawing is the layout problem. We can

transform therelation between pathway components

into a directed graph, and the drawing problem then

becomes a graph layout problem. There are two

well-known graph layout approaches: hierarchical

layout (Sugiyama et al., 1981; Eades and Sugiyama,

1990; Carmel et al., 2004) and forced directed layout

(Fruchterman and Reingold, 1991; Gansner and

North, 1998). However, both approaches can only

handle simple pathway structures such as hierarchies

and cycles. Recently, a number of approaches (Karp

and Paley, 1994; Becker and Rojas, 2001; Li and

Kurata, 2005; MetaCyc Encyclopedia of Metabolic

Pathways, 2008) have been proposed to layout

pathways. Karp and Paley (Karp and Paley, 1994)

gave a pioneering work in which they pointed out

that rather than searching for one single, all-purpose

graph layout algorithm, different algorithms should

be applied to parts of the pathway with different

topologies. They devised an algorithm for drawing

metabolic pathways which breaks the graph into

cyclic, linear and tree-structured components and

then applies different layout methods to each of

these individually. Their algorithm has been

implemented in MetaCyc (MetaCyc Encyclopedia of

Metabolic Pathways, 2008) that will be used in this

paper as a baseline to evaluate our approach. Becker

and Rojas (Becker and Rojas, 2001) presented an

algorithm that combines circular, hierarchical and

force-directed layouts. Their approach is particularly

designed for pathways that have a main cycle. Li

and Kurata (Li and Kurata, 2005) proposed a LK-

grid layout algorithm that applies force-directed

layout over grid points. They employed a cost

function defined over connection structures in the

graph. LK-grid layout is the first algorithm to

produce clustered layouts in which nodes involved

in the same functional module are clustered together.

LK-grid layout has been integrated into CADLIVE

(CADLIVE, 2008) for automatic generation of

pathway visualization. However, as observed from

the examples in (CADLIVE, 2008), LK-grid layout

135

Tsay J., Wu B. and Huang G. (2010).

HOLY-II: IMPROVED HIERARCHICALLY ORGANIZED LAYOUT FOR VISUALIZATION OF BIOCHEMICAL COMPLEX PATHWAYS.

In Proceedings of the First International Conference on Bioinformatics, pages 135-140

DOI: 10.5220/0002725501350140

 SciTePress

can induce large number of edge crossings, and local

structures, such as hierarchies and cycles, are not

clearly visualized. Kato, Magasaki, Doi and Miyano

(Kato et al., 2005) presented an improved grid

layout algorithm that reduces the number of

crossings, and incorporates subcomponent

information. In this paper, we aim to develop new

layout algorithms that produce clustered layouts,

reduce edge crossings, and render global structures

as well as local structures nicely.

Observe that many complex pathways are

described as hierarchical structures in which a

pathway is recursively partitioned into several sub-

pathways, and organized hierarchically as a tree. The

hierarchical structure provides a natural way to

visualize the global structure of a complex pathway.

Recently, Tsay et al. (Tsay et al., 2009) presented

the first hierarchically organized layout, HOLY, that

takes the advantages of the hierarchical structures

inherent in complex pathways, and produces

clustered layouts that render both global structures

and local structures nicely. In this paper, we present

a new hierarchically organized layout algorithm,

HOLY-II, which improves HOLY-I for complex

pathways. Our main contribution is the development

of new algorithms for joining layouts. Experiment

shows that our approach can clearly render the

global structure of complex pathways as well as the

local structure in each sub-pathway, and gives better

visualization for many examples from MetaCyc and

CADLIVE. Furthermore, with the joining capability

of our approach, one is able to visualize any

collection of pathways, selected from pathway

databases, to study their interactions.

The remainder of this paper is organized as

follows. Section 2 reviews pathway visualization

and conventional layout algorithms. Section 3

presents our hierarchically organized layout

algorithm. Section 4 gives experimental results, and

section 5 concludes.

2 PATHWAY VISUALIZATION

We follow the Petri Net representation of pathways

(Pinney et al., 2003) that consists of two types of

nodes: place nodes and transition nodes. Place nodes

represented as circles denote compounds, and

transition nodes represented as boxes denote

reactions. Reaction nodes are labelled by Enzyme

Commission numbers (EC numbers). A Petri Net

becomes a directed graph if we treat both place

nodes and transition nodes as the same. The problem

of pathway layout thus becomes a graph layout

problem.

Layout is a transformation from topology to

geometry; that is, it generates coordinates for

components. Forced-directed layout (Kamada and

Kawai, 1989; Gansner and North, 1998;

Fruchterman and Reingold, 1991) is one of the

widely used methods to produce a two-dimensional

layout. The basic idea is to model a graph as a

physical system where the nodes are repulsive

particles and the edges are attractive interactions. All

the repulsive and attractive interactions are

represented by an energy function. The algorithm

iterates to update node coordinates by calculating all

repulsive and attractive forces, and the graph will

iteratively become a regular shape. A layout is

determined when the forces drive the system to a

steady state (a local minimum of energy). Force-

directed layout can be applied to both directed

graphs and undirected graphs, and results in layouts

with the following aesthetic properties (Fruchterman

and Reingold, 1991): distribute the vertices evenly

in the frame, minimize edge crossings, make edge

lengths uniform, reflect inherent symmetry and

conform to the frame. In this paper, we will use

force-directed layout for pathways that are mainly

cycles.

Hierarchical layout (Sugiyama et al., 1981;

Eades and Sugiyama, 1990; Carmel et al., 2004;

Friedrich and Schreiber, 2004) is another widely

used method that features producing a layered

downward diagram and highlighting the main

direction or flow within a directed graph. Cyclic

dependencies of nodes will be automatically

detected and resolved. Nodes will be placed in

hierarchically arranged layers. Additionally, the

ordering of the nodes within each layer is chosen in

such a way that the number of edge crossings is

small. In this paper, we will use hierarchical layout

for pathways that are hierarchies.

Some research (Masui, 1994; Barreto and

Barbosa, 2000) has proposed to integrate

evolutionary search, such as genetic algorithms.

Though this kind of approaches could intuitively

achieve a nice solution, running time is still an issue

when drawing large graphs. We will not consider

them in this paper.

3 HIERARCHICALLY

ORGANIZED LAYOUT

In this section, we present our layout algorithm

HOLY-II for hierarchically organized pathways that

BIOINFORMATICS 2010 - International Conference on Bioinformatics

136

Figure 1: The hierarchical organization of super-pathway

of Glycolysis/TCA/Glyox-Bypass.

are recursively partitioned into sub-pathways, and

represented as trees. HOLY-II was implemented in

Java with Eclipse platform (Eclipse.org, 2007). It is

able to run under both Windows XP and Linux.

As in HOLY, HOLY-II assumes that a complex

pathway is hierarchically organized as a tree. For

example, the tree in Figure 1 represents a

hierarchically organized pathway that consists of

three sub-pathways, GLYCOLYSIS and

TCA/GLYOX-BYPASS and PYRUVDEH-RXN.

The sub-pathway TCA/GLYOX-BYPASS is

composed of two sub-pathways, TCA and GLYOX-

BYPASS. HOLY-II performs the following three

major stages to produce layouts for hierarchically

organized pathways.

 The Decomposition Stage that decomposes a

hierarchically organized pathway into

hierarchical groups of components.

 The Layout Stage that produces layouts for

basic components.

 The Joining Stage that joins component layouts

to form a final pathway layout.

3.1 Pathway Decomposition

The objective of the decomposition stage is to

partition a pathway into component groups such that

both global structures and local structures are

preserved, and can be explored in the final layout.

The stage consists of a grouping phase and a

partitioning phase. In the grouping phase, sub-

pathways are grouped into sub-pathway groups

recursively along the hierarchical tree, starting from

the root node, until all nodes are assigned to groups.

Two types of grouping are performed: cycle

grouping and overlap grouping. Cycle grouping is to

group sub-pathways whose separation breaks global

cycles, and overlap grouping is to group sub-

pathways who are highly overlapped. Note that

cycles are important features that usually form

“backbones” of metabolic processes. We thus group

sub-pathways whose separation breaks cycles to the

same group. High degree of overlapping between

sub-pathways implies that they are highly related.

We also group highly overlapped sub-pathways to

the same group. We set 30 percent of nodes as the

threshold for overlap grouping. Consider the

pathway in Figure 1. As sub-pathway TCA and

Glyox-Bypass highly overlap each other, they will

be assigned to the same group. The grouping

procedure will produce 3 groups: two singleton

groups, one for Glycolysis and the other for

Pyruvdeh-rxn, and the group composed of TCA and

Glyox-Bypass. Note that global structures can be

naturally preserved as sub-pathway grouping is

performed along hierarchical trees.

Each sub-pathway group identified in

grouping phase defines a group pathway that is the

union of all sub-pathways in that group. In the

partitioning phase, we examine each group pathway.

If the group pathway contains cycles, we then

partition the pathway into components so that cycles

are extracted and preserved. In particular, we will

first partition the group pathway into strongly

connected components, and then connect trivial

components to form maximal acyclic components.

The stage produces a tree of component groups.

Each component is either strongly connected or

acyclic.

3.2 Component Layout

In the layout stage, HOLY performs layout on each

component. We use force-directed layout for

strongly connected components to emphasize

symmetry and uniform edge lengths, and

hierarchical layout for acyclic components to stress

the direction and flow within a directed graph. With

careful selection of algorithms, our implementation

is able to produce layout in real time.

For efficiency, we use the force-directed layout

developed by Koren and Harel (Koren and Harel,

2003). Unlike traditional node-by-node optimization

(Kamada and Kawai, 1989), Koren and Harel use

the idea of axis-by-axis optimization, which is a one-

dimensional optimization and runs much faster.

Their method can be used for two-dimensional graph

layout by interleaving 1-D optimizations on x-

coordinate and y-coordinate.

For hierarchical layout, we use the algorithm

developed by Sugiyama, Tagawa and Toda

(Sugiyama et al., 1981) that consists of four major

steps: cycle removal, layering, crossing reduction, x-

coordinate assignment. We use the greedy method

(Eades and Sugiyama, 1990) to remove cycles and to

layer nodes. As for the crossing reduction, we use

the layer-by-layer sweep approach (Eades and

Sugiyama, 1990) that keeps looping until no layer is

HOLY-II: IMPROVED HIERARCHICALLY ORGANIZED LAYOUT FOR VISUALIZATION OF BIOCHEMICAL

COMPLEX PATHWAYS

137

rearranged. However, the process to determine a

permutation between two layers is very slow. We

thus apply the barycentric (BC) heuristic (Sugiyama

et al., 1981) to find a node ordering within a layer.

3.3 Joining Component Layouts

Before joining sub-pathways, we need to place

junction nodes that connect components on the

boundary of each component layout; otherwise

joining them could cause a large number of edge

crossings. Our solution is to insert pseudo-nodes to

push junction nodes outward to the boundary of the

layout. Our node insertion has two policies: one for

cycles and the other for hierarchies. We insert

pseudo-nodes into both sides of a junction node that

is in a cycle. This will force the path containing the

junction node to get flipped outward while forced-

directed layout is performed. For hierarchies, we

simply insert pseudo-nodes between the junction

node and its parent node. Junction nodes will then be

pushed to the bottom of the layout.

To join component layouts, we traverse the tree

in a bottom-up fashion, and at each node, we join all

layouts from its child nodes. To join layouts, we

choose a layout as the first main component, and

join other layouts one at a time to the main

component. Conceptually, we need to search over all

possible joining orders to find the best result. This

will take time exponential to the number of layouts,

and will not be practical for interactive applications.

In our implementation, we determine the joining

order heuristically by priorities defined over

component sizes. The priority of a component is

defined as the number of nodes in that component,

and is doubled if it contains cycles. Note that cycles

often form “backbones” of metabolic pathways. In

that case, one usually draws the cycle first, and adds

remaining parts to the cycle. We thus give higher

priority to cycles. Experiment shows that our

approach produces nice results in real time.

Component layouts are classified into two

categories: hierarchical and cyclic. Each hierarchical

layout is abstracted as a rectangle with its junction

nodes mapped to the boundary of the rectangle.

Similarly, cyclic layouts are abstracted as circles.

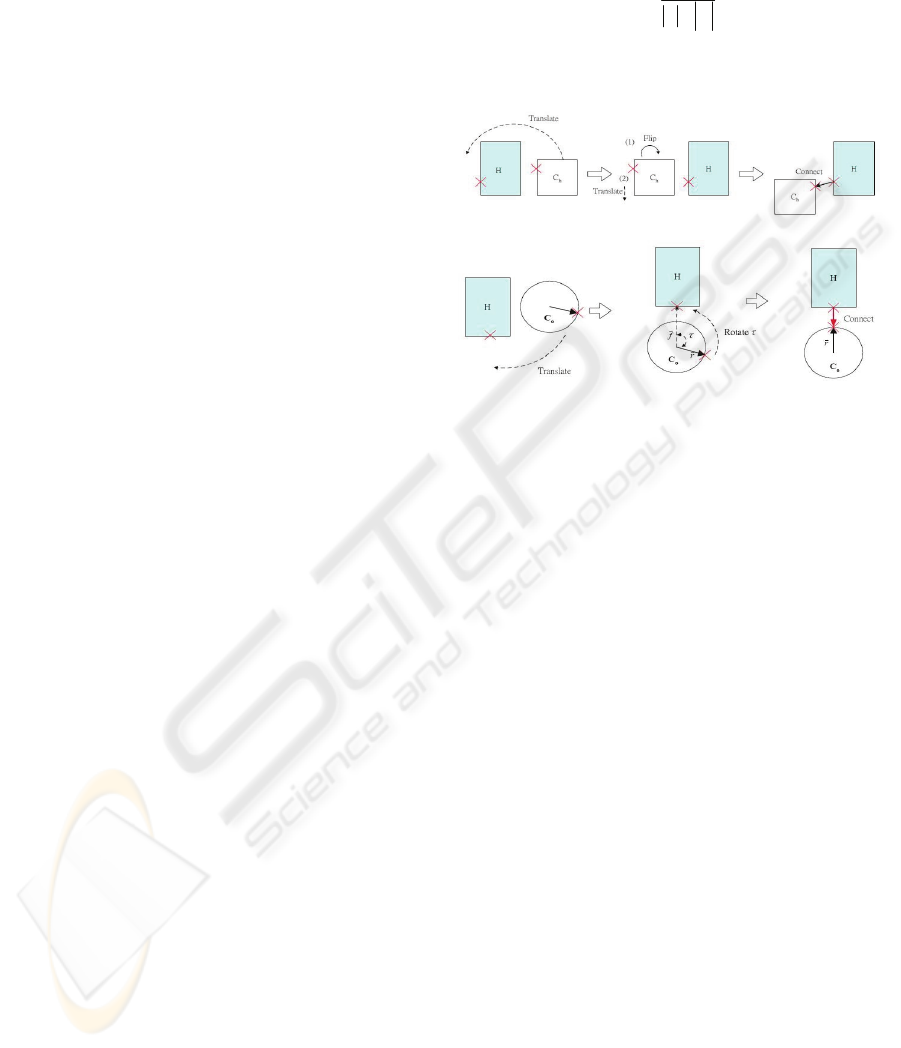
We introduce 3 operations for joining two layouts:

translation, rotation and flipping, and develop rules

to apply these operations to join layouts. Rules are

selected based on layout categories and relative

positions of junction nodes. Figure 2(a) illustrates

one of the rules to join two hierarchical layouts. The

red crosses denote the junction nodes. Translation

and flipping are applied to perform the join. Figure

2(b) illustrates one of the rules, which applies

translation and rotation to attach a cyclic layout to a

hierarchical layout. The rotation angleτcomputed

as equation 1.

)

arccos(

(1)

where

and

denote the vectors from the centroid

of the cyclic layout to the junction nodes.

(a)

(b)

Figure 2: Illustrations of rules for (a) joining two

hierarchical layouts, and (b) joining a cyclic layout to a

hierarchical layout.

4 EXPERIMENTAL RESULTS

We compare layouts produced by HOLY-II and

examples from CADLIVE (CADLIVE, 2008), a

software system for computer-aided design of living

systems, and HOLY (Tsay et al., 2009), the previous

hierarchically organized layout.

4.1 Comparison to CADLIVE

We compare HOLY-II and CADLIVE for the

metabolic pathway given in (CADLIVE, 2008)

which consists of (1)pentose-phosphate,

(2)glycolysis and (3)TCA cycle. Figure 3 gives the

result. Both HOLY-II and CADLIVE successfully

produce clustered pathway layouts in which nodes in

the same sub-pathway are clustered together.

However, HOLY produces much better layout inside

each cluster. In the layout from CADLIVE, reactions

(arcs) are entangled with each other, and the

structure of each cluster is difficult to read. In the

layout from HOLY, the sub-pathway in component

(1) is drawn as a layout of multiple hierarchies,

which reveals the real inner structure of that sub-

pathway. The main structure of component(2) is a

long path, and component (3) consists of two

overlapped cycles.

BIOINFORMATICS 2010 - International Conference on Bioinformatics

138

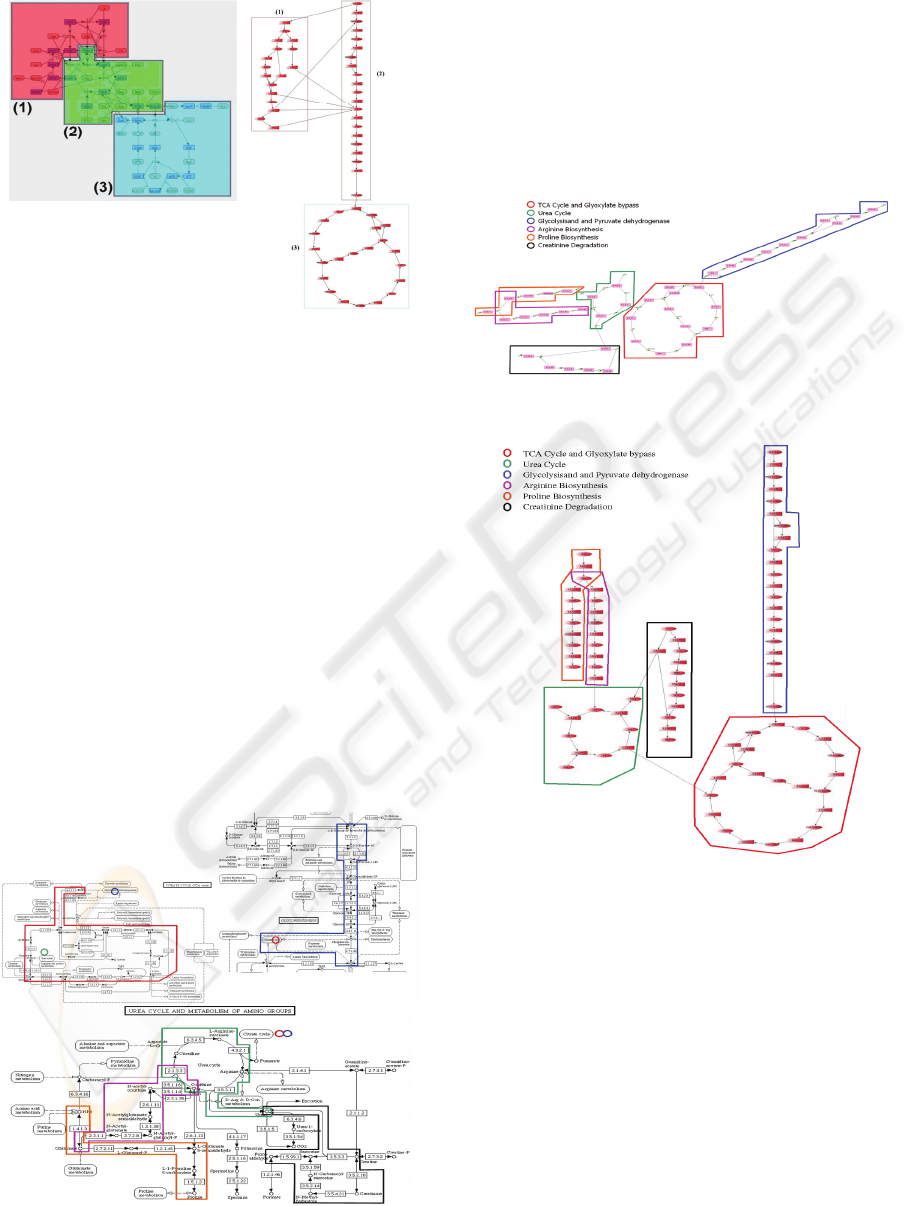
Figure 3: Comparison of layouts produced by

CADLIVE(a) and HOLY-II(b).

4.2 Comparison to HOLY

In Kyoto Encyclopedia of Genes and Genomes

(KEGG) (Kanehisa and Goto, 2000), pathway maps

are drawn by human, and stored in the computer for

retrieval. It is difficult to take several pathways from

the databases, and study their relations in KEGG. In

HOLY-II, it is easy to join pathways selected from

databases, For example, consider a set of selected

pathways that consists of 6 pathways: (1)TCA Cycle

and Glyoxylate bypass, (2)Urea Cycle,

(3)Glycolysisand and Pyruvate dehydrogenase,

(4)Arginine Biosynthesis, (5)Proline Biosynthesis

and (6)Creatinine Degradation. Note that in KEGG,

these pathways are distributed in several maps as

shown in Figure 4. It is difficult to study their

interactions in maps from KEGG.

Figure 4: Layouts are distributed in different maps from

KEGG.

With the joining capability of HOLY and

HOLY-II, one can join these pathways, visualize and

study their relations in one map. Figure 5 and 6

gives the visualization of the pathways selected from

KEGG by HOLY and HOLY-II, respectively. Note

that the visualization produced by HOLY-II is more

compact, and the directions of arcs are more

consistent than the visualization produced by HOLY.

Figure 5: Joining of pathways selected from KEGG by

HOLY.

Figure 6: Joining of pathways selected from KEGG by

HOLY-II.

5 CONCLUSIONS

Experiment shows that HOLY-II is able to give

comprehensible visualization for pathways with

hierarchies, cycles as well as complex structures. In

addition, HOLY-II runs very fast, and has been used

in (Jeng, 2006) to develop an interactive pathway

visualization system.

(a) (b)

HOLY-II: IMPROVED HIERARCHICALLY ORGANIZED LAYOUT FOR VISUALIZATION OF BIOCHEMICAL

COMPLEX PATHWAYS

139

ACKNOWLEDGEMENTS

Part of this research was supported by National

Science Council, Taiwan, ROC, under grant NSC

98-2221-E-194-064-.

REFERENCES

Barreto, A.M.S. and Barbosa, H.J.C., 2000. Graph Layout

Using a Genetic Algorithm. In VI Brazilian

Symposium on Neural Networks IEEE Computer

Society. Los Alamitos, USA, 179-184.

Becker M.Y. and Rojas I., 2001. A Graph Layout

Algorithm for Drawing Metabolic Pathways. In

Bioinformatics, 17(5), 461-467.

Brandenburg F.J., Forster M., Pick A., Raitner M., and

Schreiber F., 2004. Biopath: Exploration and

Visualization of Biochemical Pathways. In Graph

Drawing Software, Mathematics and Visualization.

Springer Verlag.

CADLIVE, 2008. http://kurata21.bse.kyutech.ac.jp/cadlive

(Accessed: 10, July 2008).

Carmel L., Harel D. and Koren Y., 2004. Combining

Hierarchy and Energy for Drawing Directed Graphs.

IEEE Transactions on Visualization and Computer

Graphics, 10(1) 46-57.

Eades P. and Sugiyama K., 1990. How to draw a directed

graph, Journal of information processing 13(4), 424-

437.

Eclipse.org, 2007. http://www.eclipse.org/ (Accessed: 5,

August 2007).

Friedrich C. and Schreiber F., 2004. Flexible Layering in

Hierarchical Drawings with Nodes of Arbitrary Size.

In 27th Conference on Australasian Computer Science

ACM, New York, 369-376.

Fruchterman T. and Reingold E., 1991. Graph Drawing by

Force-Directed Placement. Software-Practice and

Experience, 21(11), 1129- 1164.

Gansner E.R. and North S.C., 1998. Improved Force-

directed Layouts, International Symposium on Graph

Drawing, Lecture Notes In Computer Science. 1547,

Springer-Verlag, Germany, 364 – 373.

Jeng Y.S., 2006. VisualPathway: Biochemical Pathway

Layout and Visualization System. Master Thesis,

Department of Computer Science and Information

Engineering, National Chung-Cheng University, 2006.

Kamada T. and Kawai S., 1989. An algorithm for drawing

general undirected graphs. In Information Processing

Letters 31(1),7-15.

Kanehisa M. and Goto S., 2000. KEGG: Kyoto

Encyclopedia of Genes and Genomes. In Nucleic

Acids Research. Oxford University Press, 28(1), 27-

30.

Karp P.D. and Paley S., 1994. Automated Drawing of

Metabolic Pathways. In The 3rd Intl. Conference on

Bioinformatics and Genome Research World Scientific

Publishing Company, New Jersey, 225-238.

Kato M., Magasaki M., Doi A., and Miyano S., 2005.

Automatic Drawing of Biological Networks Using

Cross Cost and Subcomponent Data. In Genome

Informatics

16(2), 22-31.

Koren Y. and Harel D.,2003. Axis-by-Axis Stress

Minimization. In 11th Inter. Symposium on Graph

Drawing Springer Verlag, Germany, 450-459.

Li W. and Kurata H., 2005. A Grid Layout Algorithm for

Automatic Drawing of Biochemical Networks. In

Bioinformatics 21(9), 2036-2042.

Masui T., 1994. Evolutionary Learning of Graph Layout

Constraints from Examples. In ACM Symposium on

User Interface Software and Technology ACM, New

York, 103-108.

MetaCyc Encyclopedia of Metabolic Pathways, 2008.

http://metacyc.org/ (Accessed: 10, July 2008).

Pinney J.W., Westhead D.R., and McConkey G.A., 2003.

Petri Net Representations in Systems Biology. In

Biochemical Society Transactions 31(6),1513-1515.

Salamonsen W., Mok K., Kolatkar P., and Subbiah S.,

2004. BioJAKE: A Tool for the Creation,

Visualization and Manipulation of Metabolic

Pathways. In Pacific Symposium on Biocomputing.

World Scientific Publishing Company, New Jersey,

392-400.

Suderman M. and Hallett M., 2007. Tools for Visually

Exploring Biological Networks. In Bioinformatics,

23(20), 2651-2659.

Sugiyama K., Tagawa S., and Toda M.,1981. Methods for

Visual Understanding of Hierarchical Systems. IEEE

Transactions on Systems, Man, and Cybernetic, SMC,

11(2), 109-125.

Sugiyama K., 1987. A Cognitive Approach for Graph

Drawing. In Cybernetics and Systems: An

International Journal, 18 (6) ,447-488.

Trost E., Hackl H., Maurer M., and Trajanoski Z, 2003.

Java Editor for Biological Pathways, Bioinformatics 19(6).

Tsay J.J., Wu B.L. and Jeng Y.S., 2009. Hierarchically

Organized Layout for Visualization of Biochemical

Pathways. accepted for publication in International

Journal Artificial Intelligence in Medicine.

BIOINFORMATICS 2010 - International Conference on Bioinformatics

140