
CODING BIOLOGICAL SYSTEMS IN A STOCHASTIC
FRAMEWORK
The Case Study of Budding Yeast Cell Cycle
Alida Palmisano
The Microsoft Research - University of Trento, Centre for Computational Systems Biology
Piazza Manci 17, 38123 Trento, Italy
Dept. of Information Engineering and Computer Science, University of Trento, via Sommarive 14, 38123 Trento, Italy
Keywords:
Budding yeast, Cell cycle, Stochastic simulation, BlenX.
Abstract:
In biology, modelling is mainly grounded in mathematics, and specifically on ordinary differential equations
(ODEs). Using programming languages originally thought to describe networks of computers that exchange
information is a complementary and emergent approach to analyze the dynamics of biological networks. In
this work, we focus on the process algebra language called BlenX and we show that it is possible to easily re-
use ODE models within this framework. In particular we focus on a well characterized biological network: the
cell cycle of the budding yeast. This system has been studied in great details in the deterministic framework
and data about a lot of mutants are available for the chosen model. It is interesting to note that the experimental
phenotypic characterization of some mutants cannot be explained by the deterministic solution of the model,
so in this work we propose a translation of the model in the stochastic framework in order to be able to verify
if the inconsistencies are due to the noise that is affecting the system.
1 INTRODUCTION
In the last decade, the classical approach to model
biological systems using mathematical formalisms in
which continuous variables evolve deterministically
was proved to be not enough for explaining the be-
havior of some molecular mechanisms in which the
population of elements is so small that their stochastic
variation in time can lead the system to behave differ-
ently from the average (McAdams and Arkin, 1997).
Moreover, as a recent paper on Nature (Nurse,
2008) points out, not only the kind of the results of
a model are important but also the way in which it
is formalized should be taken carefully into account:
according to him, indeed, life science field requires
the development of new and more appropriate lan-
guages to describe biological systems. After the work
of Regev et al. (Regev and Shapiro, 2002), a promis-
ing trend in this direction is to use technologies based
on programming language theories in order to capture
the intrinsic concurrency, causality and probabilistic
nature into algorithmic descriptions that can be exe-
cuted, analyzed and simulated by computers. Algo-
rithmic approaches require modelers to think about
the mechanisms governing the behavior of the sys-
tem under question (Priami, 2009): this strategy di-
verges from classical mathematical modeling because
it is executable and not just simply solvable (Fisher
and Henzinger, 2007). Mathematical equations de-
scribe the variation of variables (i.e. concentrations
of species) from one state to another, while exe-
cutable models highlight the causality relation among
the events that constitute the history of the dynamics
of the model. As a consequence, a number of pro-
cess calculi have been adapted or newly developed for
building biological models and performing stochastic
simulations (i.e. stochastic pi-calculus (Priami et al.,
2001), BioAmbients (Regev et al., 2004), Brane Cal-
culi (Cardelli, 2005), CCS-R (Danos and Krivine,
2004), k-calculus (Danos and Laneve, 2004), Bio-
PEPA (Ciocchetta and Hillston, 2007)). In this work,
we will use a new programming language, BlenX,
(Dematt
´
e et al., 2008), that is evolved from stochas-
tic pi-calculus and Beta Binders (Priami and Quaglia,
2005). This language follows the main paradigms of
process calculi and defines some new primitives that
allow an easy encoding of deterministic models pre-
sented in the literature in a stochastic framework.
The biological system on which we want to focus
our study is the well known molecular network driv-
153
Palmisano A. (2010).
CODING BIOLOGICAL SYSTEMS IN A STOCHASTIC FRAMEWORK - The Case Study of Budding Yeast Cell Cycle.
In Proceedings of the First International Conference on Bioinformatics, pages 153-159
DOI: 10.5220/0002739601530159
Copyright
c
SciTePress

ing the cell cycle of Saccharomyces cerevisiae. In the
literature (see (Csikasz-Nagy, 2009) for a state of the
art review), beside models written in terms of ordinary
differential equations (ODE) (Nasmyth, 1996), we
find stochastic cell cycle models built with Langevine
type stochastic DE (Steuer, 2004), with the Gillespie
method (Sabouri-Ghomi et al., 2007; Kar et al., 2009)
and with stochasticity on transitions (Lecca and Pri-
ami, 2007; Mura and Csikasz-Nagy, 2008a). How-
ever the most complete model of this system (Chen
et al., 2004a) has only been studied in the determinis-
tic framework and, as recent studies on reduced mod-
els suggest (Kar et al., 2009), the noise can have an
important impact on the behaviour of the system.
The main contribution of this paper is, therefore,
a codification in the BlenX language of the model de-
scribed in (Chen et al., 2004a) and some interesting
analysis that can be performed on the simulation runs
of the BlenX model.
2 THE BLENX LANGUAGE
A detailed description of the BlenX language is out of
the scope of this paper. We just summarize the sub-
part of BlenX needed for understanding the code pre-
sented below. We refer the reader to (Dematt
´
e et al.,
2008; Dematt
´
e et al., 2008) for the formalization of
the language and its modeling approach, and for a de-
scription of the tools that support this language.
The basic metaphor of BlenX is that a biologi-
cal entity (i.e. a component that is able to interact
with other components to accomplish some biologi-
cal functions) is represented by a computational de-
vice called box that has a set of interfaces and an in-
ternal program. Interfaces have associated types and
they are used by an entity to interact with other en-
tities; the internal program, instead, codifies for the
set of actions that a box can perform after a specific
interaction with another entity in the system. For
example, if a box is modeling a protein, its inter-
faces may represent sensing and effecting domains.
Through sensing domains the protein receives sig-
nals that are then propagated through the internal ac-
tions that activate/inactivate a specific effecting do-
main. The exchange of signals can happen between
boxes whose interfaces have a certain degree of affin-
ity, which codes the strength of their interaction. Each
action/event in BlenX is associated to a rate function
used to run stochastic simulation of the coded system
using a variant of the Gillespie algorithm. The rate
functions can be declared as simple real numbers if
the reaction that they are modeling is a simple mass
action law, or they can be arbitrary functions (e.g.
Michaelis-Menten, Hill response) if the reaction is an
aggregated process whose elementary mechanism of
interaction between entities is not known.
The primitives of the language used in Sect. 3 for
the translation from ODEs to BlenX are graphically
summarized in Fig. 1(b).
(a) (b)
Figure 1: (a) Boxes as abstractions of biological entities.
The small squares on the border are the interfaces; x and
y are the interfaces subjects (omitted when not necessary);
A and C are the interfaces types (omitted when not nec-
essary); the line surrounding C indicates that the interface
is hidden; P is the internal program and B is the name of
the box; (b) Intuitive behaviour of some BlenX primitives.
Each row represents one of the primitives used in our trans-
lation. The first codifies the interaction between two boxes,
through the exchange of an input/output signal (input is in
the form of b?() and the output is in the form a!()). The
last three rows are the graphical representation of events of
the form: “when(conditions) verb”, where the action verb
is triggered when conditions are satisfied. The verb can be
one of split/join, new or delete, that model respectively the
substitution, creation, and deletion of boxes in the system.
Conditions are in the form of “entity
name : : function”,
whose meaning is that the action after the condition is trig-
gered, at rate function, on the entity entity name.
The last peculiar feature of the BlenX language
that we will use later in the code are templates, that
are a feature of many programming languages that al-
lows to code parametric processes which can contain
variable parts instantiated later by the compiler with
respect to the base grammar. In BlenX template code
is specialized and instantiated at compile time using
interfaces identifiers, code or names that are passed
as template arguments. As we will see in the next
section, the usage of templates reduces the amount of
code that need to be written and it makes the whole
model more modular and easy to be modified.
3 REGULATORY NETWORK OF
SACCHAROMYCES CEREVISIAE
The cell cycle is a coordinated set of steps by which a
cell replicates all its internal components and divides
them into two nearly identical daughter cells so that
each of them contains the molecular machinery nec-
essary to repeat the process. The cell cycle mecha-
nism of the budding yeast is one of the most under-
BIOINFORMATICS 2010 - International Conference on Bioinformatics
154

stood control system between eukaryotes (Csikasz-
Nagy, 2009) and its function is constrained by the
phenotypic properties of more than 100 genetically
engineered strains. In (Chen et al., 2004a), the au-
thors show a mathematical model built on this con-
trol system that is successfully explaining the pheno-
types of a lot of mutants characterized so far but some
inconsistencies between the model and experiments
indicate aspects of the mechanism that require more
careful studies. Moreover given the small size of a
yeast cell, the number mRNA molecules for most of
the regulatory proteins is very low (possibly less than
10) and the total number of molecules of each regula-
tory protein in a cell is quite low (Kar et al., 2009): the
intrinsic molecular fluctuations are then probably the
main responsible for the fluctuation in cell cycle prop-
erties like the size at division. (Kar et al., 2009) also
point out that although comprehensive deterministic
models of the control system are available for bud-
ding yeast, stochastic simulations have not been car-
ried out because the full reaction network needs to be
expressed in terms of elementary reaction steps in or-
der to perform exact stochastic simulations that takes
precisely into account the effect of the intrinsic noise.
Although this consideration is generally true, we want
to make a remark, already discussed by several au-
thors (Arkin and Rao, 2003; Ciocchetta and Hillston,
2007; Mura, 2008), about the usage of the Gille-
spie SSA algorithm (Gillespie, 1977) when high-level
mathematical representation of non-elementary reac-
tions are incorporated in the form of rate-dependent
functions. The rate dependent functions are defin-
ing the reaction propensities of the stochastic model.
Following the approach of (Mura and Csikasz-Nagy,
2008b) who model a smaller version of the cell cycle
mechanism studied in this work, we assume that the
fundamental hypothesis of Gillespie holds, i.e. each
reaction time is a random variable following a neg-
ative exponential distribution with rate equal to the
value of the propensity function. If this hypothe-
sis is valid, a stochastic characterization of the reac-
tion times as negatively distributed random variables
is an accurate modeling choice, as proved by Gille-
spie (Gillespie, 1977). In our case, because of the
presence of many non-elementary reactions, a care-
ful validation of the stochastic model has been per-
formed: here just few examples are shown for the sake
of conciseness and because the main focus of the pa-
per is the modeling procedure. Detailed studies on all
the experimentally characterized mutants described at
(Chen et al., 2004b) and (Panning et al., 2008) are
a work in progress and some preliminary results are
presented in section 4. Moreover an “unpacking” of
all the non-elementary reaction mechanisms into their
elementary steps is part of our future studies: we will
use the model described here as the starting compo-
nent of an iterative modeling cycle that starts from
the model with abstracted complex mechanisms and
refines it until it contains only elementary reactions.
This is a complementary approach w.r.t. the one of
(Kar et al., 2009) who are studying simplified version
of the mechanism and they increase the general com-
plexity of the model at each iterative modeling step.
Before explaining the modeling procedure that
has been followed to code the cell cycle network
in BlenX, we briefly summarize the biological back-
ground of the chosen system, referring the reader to
(Chen et al., 2004a) for all the details about the mathe-
matical model, its parameters and more detailed stud-
ies in the deterministic framework.
Newborn daughter cells must reach a critical size
to have enough Cln3 and Bck2 protein to activate the
transcription factors which drive synthesis of Cln2
and Clb5. Cln2 is primarily responsible for bud emer-
gence and Clb5 for initiating DNA synthesis. In G1
phase Clb5 is not active because inhibited by CKIs.
After the CKIs are phosphorylated by Cln2, they are
rapidly degraded allowing Clb5 to do its job. Other
cyclins like Clb2 are not present in G1-phase because
their transcription factor is inactive, their degradation
pathway Cdh1/APC is active, and their stoichiomet-
ric inhibitors CKI are abundant. Cln2- and Clb5-
dependent kinases remove CKI and inactivate Cdh1,
allowing Clb2 to accumulate and it activates its own
transcription factor. Clb2 turns off the transcription
factors of Cln2 and Clb5. As Clb2 drives the cell into
mitosis, it also stimulates the synthesis of Cdc20 that,
when the replicated chromosomes are attached, will
initiates mitotic exit, degrading Pds1 and releasing a
protease involved in sister chromatid separation. It
also degrades Clb5 and partially Clb2, lowering their
potency on Cdh1 inactivation. As the attached chro-
mosomes are properly aligned on the metaphase spin-
dle, Tem1 is activated, which in turn activates Cdc15,
which in turn phosphorylates Net1 and this releases
its hold on Cdc14. Cdc14 then does battle against the
Cdks: activating Cdh1, stabilizing CKIs, and activat-
ing their transcription factor. In this manner, Cdc14
returns the cell to G1 phase (no cyclins, abundant
CKIs, and active Cdh1). The mathematical model of
this system contains 36 equations that are accounting
for regulatory proteins, like the ones described above,
and some dummy variables tracking specific events in
the cell cycle progress. For example, BUD is account-
ing for the activity of Cln2 (when BUD = 1, a new bud
is initiated); ORI (related to Clb5) represents the state
of origins of replication (when ORI = 1, DNA synthe-
sis is initiated); at cell division, when the concentra-
CODING BIOLOGICAL SYSTEMS IN A STOCHASTIC FRAMEWORK - The Case Study of Budding Yeast Cell Cycle
155

tion of Clb2+Clb5 drops below a threshold level, ORI
is reset to zero as origin relicenses. Finally, SPN rep-
resents the alignment of replicated chromosomes on
the mitotic spindle and it is driven by Clb2 activity.
The ODEs that formalize the biochemical net-
work described above can be easily translated in
BlenX following the codification procedure explained
in (Palmisano et al., 2009): here, we show the transla-
tion of few reactions (see Fig. 2), referring the reader
to the work mentioned above for further details.
d[Esp1]
dt
= . . . − k
as,esp
[Esp1][Pds1]
d[Pds1]
dt
= . . . − k
as,esp
[Esp1][Pds1] − k
0
d1, pds
[Pds1]+
− k
00
d2, pds
[Cdc20][Pds1] − k
00
d3, pds
[Cdh1][Pds1]
d[PE]
dt
= . . . + k
as,esp
[Esp1][Pds1]
//.prog
when(PDS1, ESP1 : : Assoc_to_form_PE) join(PE);
when(PDS1 : : degradation_1_PDS1) delete(1);
when(PDS1 : : degradation_2_PDS1) delete(1);
when(PDS1 : : degradation_3_PDS1) delete(1);
//.func
let Assoc_to_form_PE:function = kasesp*alpha*|PDS1|*|ESP1|;
let degr_1_PDS1:function = kd1pds_p*|PDS1|;
let degr_2_PDS1:function = kd2pds_p_p*alpha*|CDC20|*|PDS1|;
let degr_3_PDS1:function = kd3pds_p_p*alpha*|CDH1|*|PDS1|;
Figure 2: Partial network of reaction involving Pds1 (ODE
on top left, cartoon representation on top right, BlenX cod-
ification on the bottom). The formation of the complex PE
from the single species Pds1 and Esp1 is modelled in the
ODEs with the three terms that contain k
as,esp
rate (written
in the ODEs associated to each involved species); in BlenX
this complex formation is coded with just a single join event
(with stochastic rate defined by the Assoc to form PE
function). The three degradation mechanisms of Pds1 (i.e.
spontaneous at rate k
0
d1, pds
, catalyzed by Cdc20 at rate
k
00
d2, pds
and catalyzed by Cdh1 at rate k
00
d3, pds
) are coded in
BlenX with three different delete event with the appropriate
stochastic rate.
The whole model can be translated following the
rules in (Palmisano et al., 2009), but because of the
size of the model, this can lead to a pretty complex
model, difficult to be maintained and integrated in
other models. In order to have a more effective cod-
ification, we can improve the structure of the entire
model without changing the underlying mathematical
interpretation. A way for doing that is to recognize
that there are some mechanisms that are “structurally
equal” even if applied on different proteins: for exam-
ple there are a lot of species that are degraded because
of the interaction of another species with a mass ac-
tion kinetic law. In BlenX this can be coded in an easy
way through the usage of the templates. Let’s con-
sider the degradation of Clb2 and Clb5 proteins: in
the first version of the code, the spontaneous degrada-
tion mechanism and the catalyzed one has been trans-
lated for both proteins with a delete event whose rate
is depending on kdb2 p, kdb5 p, kdb2p, kdb5 p p
respectively. We can drop those four events and code
the mechanisms with the code in Fig. 3 (details about
the interpretation of the code are given in the caption
of the figure).
//.prog
template receiving_degr_sign : pproc<<name channel>>
= channel?().die;
template spont_degradation : pproc<<rate kin_rate>>
= die(rate(kin_rate));
let CLB2 : bproc = #(clb2_ch, CLB2_ty)
[ receiving_degr_sign<<clb2_ch>> |
spont_degradation<<kdb2_p>> | ... ];
let CLB5 : bproc = #(clb5_ch, CLB5_ty)
[ receiving_degr_sign<<clb5_ch>> |
spont_degradation<<kdb5_p>> ];
let CDC20 : bproc = ..., #(cdc20_out, CDC20_out_ty),...
[ ... | rep cdc20_out!().nil ];
//.types
(CLB2_ty, CDC20_out_ty, rate(Vdb2_2)),
(CLB5_ty, CDC20_out_ty, rate(Vdb5_1))
//.func
let Vdb5_1 : const = kdb5_p_p*alpha;
let Vdb2_2 : const = kdb2p*alpha;
Figure 3: Templates for degradation mechanisms. CLB2
and CLB5 boxes contain the parallel composition of the
two different mechanisms (i.e. the spontaneous degrada-
tion, and the degradation induced by the CDC20 signal).
Both are coded using the templates defined at the begin-
ning of the .prog file that, in a general way, define the se-
quence of actions that each one has to perform (an input
on a channel and a die action for the degradation induced
by the external signal; and a die with a specific rate for the
spontaneous degradation of the box). The internal program
of CDC20 contains an infinite source of output signal: this
output is linked to the input channels of both CLB2 and
CLB5 through the rate defined in the .types file defining the
interaction stochastic rate between the pairs of types. Fi-
nally, the internal program of CLB2 and CLB5 contains the
spontaneous degradation of the box at the appropriate rate.
We want to substitute the delete event with the
code in Fig. 3 because events are global rules that
drive the deletion of a box from the system, but the
mechanism that we want to model is the “local sui-
cide” of a box that decides, from its internal code, to
disappear from the system after the interaction of an-
other specific species (in this case the one involved in
the rate of the delete event): in this way we can reduce
the amount of code that has to be written because even
if a protein is degraded by different species, its inter-
nal code can be the same and the sources of the signal
can be different (with possibly different rates). More-
over, using the templates, we can write the code that is
BIOINFORMATICS 2010 - International Conference on Bioinformatics
156

accounting for this behaviour just once, and then we
can instantiate it in different boxes just specifying the
local information that differentiate each species (in
our case the rate of the self degradation, or the channel
on which the communication is happening). The tem-
plates used in this model are accounting only for the
simple mass action kinetics because we want to keep
the same level of abstraction of the original model.
However, as a general modeling principle, writing dif-
ferent kind of mechanisms (i.e. enzymatic reactions)
in a parametric way will help the user to generate a
model that is maintainable and reusable w.r.t. a model
written only with global events and rules.
In the next section we show some validation
results on stochastic simulations of the cell cycle
model. The complete BlenX code of the model
can be downloaded at http://www.cosbi.eu/downloads/attach-
ment/CellCycleModel.zip. The three textual files can be used
to reproduce the results presented in this paper using
the BetaWorkbench: we refer the reader to (Dematt
´
e
et al., 2008) for a description of the usage of the dif-
ferent tools in the BetaWorkbench framework.
4 VALIDATION OF THE
STOCHASTIC MODEL
In this section we show that our model successfully
reproduces the behavior of wild type and mutant cells
quantitatively. At (Chen et al., 2004b), full details
about the deterministic model of the different mutants
can be found. On this website, the authors summarize
the basic experimental results on which the original
wiring diagram in (Chen et al., 2004a) is based. They
also present a set of 131 mutants built using the same
equations and parameter values of the wild type ex-
cept for those parameter changes that are dictated by
the nature of the mutation.
We performed Multiple stochastic simulative
Replications in Parallel (MRIP) of the wild type
model and of some of the mutants available. We used
MRIP approaches to speed up simulations by work-
ing out independent replications of the same stochas-
tic trajectory on multiple computers. Therefore, to
guarantee the trustworthiness and the statistical accu-
racy of the analysis, we ran a batch of 300 simulations
for each parameter set (wild type or a specific mu-
tant) and each simulation reproduces about 30 com-
plete cell cycles. In Fig. 4(a), we show the output of
a simulation run for the wild type model.
Just looking the time series of the different pro-
teins involved, we see that the simulations are repro-
ducing the solutions of the original ODE model, a part
from the stochastic noise. However, in order to be
(a) (b)
(c)
Figure 4: (a) Results of a stochastic simulation of the wild
type cell cycle model. The units are minutes and number
of molecules for the x-axis and y-axis respectively. The ex-
pected oscillatory behaviour is visualized using BetaPlotter
between time instants 400 and 800. Oscillations are con-
sistent with the the deterministic solution with variance in
the peaks of some proteins caused by the stochastic noise.
(b) Statistics of some properties of the wild type cell cycle
model. Histograms title contains the mean value of the spe-
cific property. The values of the deterministic model are:
Mass at division = 2.62, Cycle time = 101.2 min, Length
of G1 phase = 36 min, Unbudded period = 33 min. (Chen
et al., 2004b). (c) The five stages of the cell cycle, sepa-
rated by the events described as rules of viability in (Pan-
ning et al., 2008). The up/down arrow in the condition of
the triggers (lightning) identifies a rise/drop of the indicated
quantity above/below the indicated threshold level.
able to compare with a statistical accuracy the com-
puted behavior with the observed phenotype of the
cells, we perform some analysis of the simulation out-
put in order to measure some properties of the model
like the cell cycle time, the mass at division and the
length of the different phases. For each of the prop-
erties we compute the mean value and we generate an
histogram of the distribution (Fig.4(b)): we verified
that those values are in accordance with the experi-
mental ones listed in (Chen et al., 2004b).
When comparing the model with the experimen-
tal data it is important to realize that much of the data
from experiments is qualitative, usually in the form
of “the cell is viable but considerably larger than wild
type cells” or “the cell arrests in G1 phase”. So in
order to compare the simulation results with experi-
mental data, it is necessary to characterize cell cycle
properties from the changing in time of the regulatory
proteins of the model (that are the quantitative infor-
mation generated by simulation runs). We analyzed
the simulation output w.r.t. the rules for viability and
CODING BIOLOGICAL SYSTEMS IN A STOCHASTIC FRAMEWORK - The Case Study of Budding Yeast Cell Cycle
157
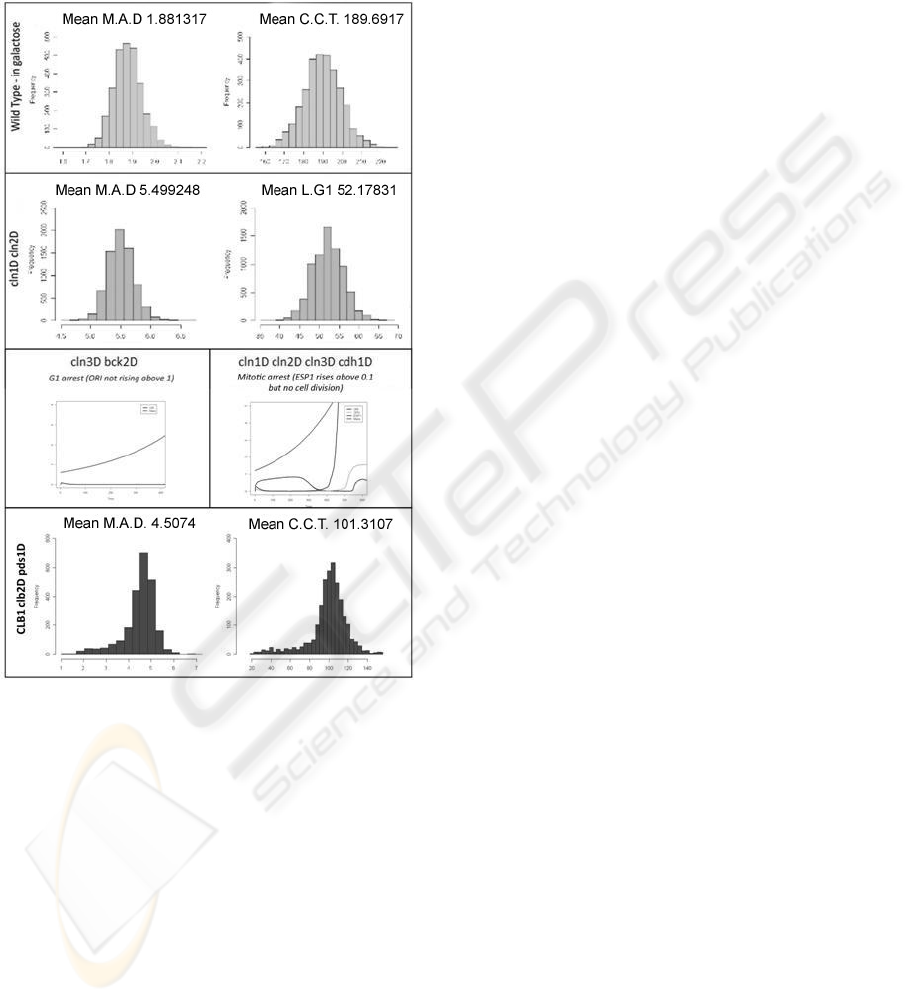
timing of phases defined in (Panning et al., 2008) and
summarized in Fig. 4(c). Setting the thresholds in this
way we were able to reproduce the statistics depicted
in Fig. 5 that, for different mutants, are in accordance
with the published phenotypic characteristics.
Figure 5: Statistics of different properties of some mutants
of the cell cycle model. Mutant 1: wild type in galactose
(Viable and, for the deterministic model, Mass at division
= 1.92, Cycle time = 189.9 min). Mutant 2: cln1∆cln2∆
(Viable and, for the deterministic model, size is 2.4X WT).
Mutant 3: cln3∆bck2∆ (Inviable, G1 arrest). Mutant 4:
cln1∆cln2∆cln3∆cdh1∆ (Inviable, Telophase arrest). Mu-
tant 5: CLB1clb2∆pds1∆ (Viable, but inconsistent with ex-
perimental results). The explaination of how to obtain the
different mutants can be found in (Chen et al., 2004b). A
detailed description of the biological meaning of those re-
sults is out of the scope of this paper, see the text for some
comments about them.
Commenting on the plots in Figure 5, we want to
point out that the third and fourth mutants are invi-
able and so all the simulations looks the same and
no statistics can be performed. The other mutants
are in accordance with the average behaviour of the
deterministic model. In particular the last inconsis-
tent mutant is viable also in the stochastic context but
it has very instable cycles (the variance of the mea-
sured properties is very high), accounting in some
way of the inviability found in the experimental out-
come: those results suggest that this mutant is a good
candidate for more careful studies on the effect of the
noise on the viability of the cell cycle machinery.
The analysis on the complete set of 131 mutants
has still to be completed, but the results on the mu-
tants showed above are promising because, from one
side, the average results are in accordance with the
results on the deterministic models, but, from the
other side, a careful analysis on the distribution of the
stochastic results can explain some of the inconsis-
tencies between the experimental result and the deter-
ministic solution of the system.
5 CONCLUSIONS
In this paper we presented the codification of a bud-
ding yeast cell cycle model in a process-algebra lan-
guage, called BlenX. This model can be stochastically
simulated in order to answer questions that cannot be
directly tackled by the deterministic approach, like
checking the partial viability of mutants at the border
of life and death, and whose mean behaviour is not
enough for completely characterize the experimen-
tal observation of the system. The simple translation
from the mathematical language is possible because
of the expressive power of BlenX that allows the def-
inition of general rate functions for reactions. How-
ever the usage of the SSA algorithm with simple and
complex kinetic laws leaves to the user the respon-
sibility to validate simulation results. The example
proposed here uses different levels of abstraction and
it has been validated against experimental results of
wild type and some mutant strains.
It is our future goal to further analyze the mecha-
nisms that are behind those complex kinetics in order
to see more in details the effect of the stochastic noise
on the system, because it can be the cause of some
inconsistencies found between the experimental re-
sults and its deterministic evolution in time. Moreover
unpacking the complex kinetics like the Michaelis-
Menten or the Goldbeter-Koshland response can be
very important both from the point of view of the
structure of the model and for the biological insights
that it can lead to. Indeed, regarding the former mo-
tivation, it can help the user to generate code that is
maintainable, reusable and more easy to be integrated
in bigger models. Regarding the latter motivation
of interest, it can make evident the need of a refine-
ment of the underlying network because, as showed
BIOINFORMATICS 2010 - International Conference on Bioinformatics
158

in (Ciliberto et al., 2007; Sabouri-Ghomi et al., 2007),
the naive unpacking of enzymatic network can lead to
network that loose their bistable behaviour unless they
are structurally modified with the addition of back-
ground reactions: so using different template to un-
pack a specific mechanism can help the biologist to
understand which is the basic structure needed for re-
covering the desired behaviour.
Finally, the complete study of all the mutants char-
acterized in (Chen et al., 2004b) is under develop-
ment: we will be able to provide to the user the
stochastic counterpart of the knowledge about the
budding yeast cell cycle discovered so far, which can
help more comprehensive studies of that system.
REFERENCES
Arkin, A. and Rao, C. (2003). Stochastic chemical kinetics
and the quasi-steady-state assumption: application to
the gillespie algorithm. Journal of Chemical Physics,
118(11):4999–5010.
Cardelli, L. (2005). In Proc. of CMSB 2004, volume 3082,
pages 257–278. LNCS.
Chen, K., Calzone, L., Csikasz-Nagy, A., Cross, F., No-
vak, B., and Tyson, J. (2004a). Integrative analysis
of cell cycle control in budding yeast. Mol Biol Cell,
15(3841-3862).
Chen, K., Calzone, L., Zwolak, J., and Tyson, J.
(2004b). Budding yeast cell cycle homepage
(http://mpf.biol.vt.edu/research/budding yeast model/pp/).
[Online; accessed August-2009].
Ciliberto, A., Capuani, F., and Tyson, J. J. (2007). Model-
ing networks of coupled enzymatic reactions using the
total quasi-steady state approximation. PLoS Comput
Biol, 3(3):e45.
Ciocchetta, F. and Hillston, J. (2007). In Proc. of FBTC
2007. ENTCS.
Csikasz-Nagy, A. (2009). Computational systems biology
of the cell cycle. Brief Bioinform, 10(4):424–34.
Danos, V. and Krivine, J. (2004). In Proc. of CONCUR
2004, volume 3170, pages 292–307. LNCS.
Danos, V. and Laneve, C. (2004). Formal molecular biol-
ogy. Theoretical Computer Science, 325(1):69–110.
Dematt
´
e, L., Priami, C., and Romanel, A. (2008). The Beta
Workbench: a computational tool to study the dynam-
ics of biological systems. Briefings in Bioinformatics.
Dematt
´
e, L., Priami, C., and Romanel, A. (2008). The
BlenX Language: A Tutorial. In LNCS, editor, SFM
2008, pages 313–365. Springer-Verlag.
Fisher, J. and Henzinger, T. (2007). Executable cell biology.
Nature Biotechnology, 25(11):1239–1249.
Gillespie, D. (1977). Exact stochastic simulation of coupled
chemical reactions. Journal of Physical Chemistry,
81(25):2340–2361.
Kar, S., Baumann, W. T., Paul, M. R., and Tyson, J. J.
(2009). Exploring the roles of noise in the eukary-
otic cell cycle. Proceedings of the National Academy
of Sciences, 106(16):6471–6476.
Lecca, P. and Priami, C. (2007). In Proc. of BioConcur
2003, volume 180, pages 51–63. ENTCS.
McAdams, H. H. and Arkin, A. (1997). Stochastic mecha-
nisms in gene expression. Proc Natl Acad Sci U S A,
94(3):814–9.
Mura, I. (2008). Technical Report TR-12-2008, CoSBi.
Mura, I. and Csikasz-Nagy, A. (2008a). Stochastic petri net
extension of a yeast cell cycle model. J Theor Biol,
254(4):850–60.
Mura, I. and Csikasz-Nagy, A. (2008b). Stochastic Petri
Net extension of a yeast cell cycle model. Journal of
Theoretical Biology.
Nasmyth, K. (1996). At the heart of the budding yeast cell
cycle. Trends Genet, 12(10):405–12.
Nurse, P. (2008). Life, logic and information. Nature,
454(7203):424–6.
Palmisano, A., Mura, I., and Priami, C. (2009). From ODEs
to language-based, executable models of biological
systems. In Proceedings of Pacific Symposium on Bio-
computing 2009.
Panning, T. D., Watson, L. T., Allen, N. A., Chen, K. C.,
Shaffer, C. A., and Tyson, J. J. (2008). Deterministic
parallel global parameter estimation for a model of the
budding yeast cell cycle. J. of Global Optimization,
40(4):719–738.
Priami, C. (2009). Algorithmic systems biology. Commun.
ACM, 52(5):80–88.
Priami, C. and Quaglia, P. (2005). Operational patterns in
beta-binders. T. Comp. Sys. Biology, 1:50–65.
Priami, C., Regev, A., Shapiro, E., and Silverman, W.
(2001). Application of a stochastic name-passing cal-
culus to representation and simulation of molecular
processes. Inform. Process. Lett., 80(1):25–31.
Regev, A., Panina, E., Silverman, W., Cardelli, L., and
Shapiro, E. (2004). Bioambients: an abstraction for
biological compartments. Theoretical Computer Sci-
ence, 325(1):141–167.
Regev, A. and Shapiro, E. (2002). Cells as computation.
Nature, 419:353–.
Sabouri-Ghomi, M., Ciliberto, A., Kar, S., Novak, B., and
Tyson, J. (2007). Antagonism and bistability in pro-
tein interaction networks. J. Theor. Biol., 250(1):209–
218.
Steuer, R. (2004). Effects of stochasticity in models of
the cell cycle: from quantized cycle times to noise-
induced oscillations. Journal of Theoretical Biology,
228(3):293–301.
CODING BIOLOGICAL SYSTEMS IN A STOCHASTIC FRAMEWORK - The Case Study of Budding Yeast Cell Cycle
159
