A NEW APPROACH FOR EPILEPTIC SEIZURE DETECTION
USING EXTREME LEARNING MACHINE
Yuedong Song
Computer Laboratory, University of Cambridge, 15 JJ Thomson Avenue, Cambridge CB3 0FD, U.K.
Sarita Azad
Department of Applied Mathematics and Theoretical Physics, University of Cambridge
Wilberforce Road, Cambridge CB3 0WA, U.K.
Pietro Lio
Computer Laboratory, University of Cambridge, 15 JJ Thomson Avenue, Cambridge CB3 0FD, U.K.
Keywords:
Epileptic seizure detection, Electroencephalogram (EEG), Discrete Wavelet Transform, Extreme Learning
Machine (ELM).
Abstract:
In this paper, we investigate the potential of discrete wavelet transform (DWT), together with a recently-
developed machine learning algorithm referred to as Extreme Learning Machine (ELM), to the task of clas-
sifying EEG signals and detecting epileptic seizures. EEG signals are decomposed into frequency sub-bands
using DWT, and then these sub-bands are passed to an ELM classifier. A comparative study on system per-
formance is conducted between ELM and back-propagation neural networks (BPNN). Results show that the
ELM classifier not only achieves better classification accuracy, but also needs much less learning time com-
pared to the BPNN classifier. It is also found that the length of the EEG segment used affects the prediction
performance of classifiers.
1 INTRODUCTION
Epilepsy, the second most common serious neurolog-
ical disorder in human beings after stroke, is a chronic
condition of the nervous system and is characterized
by recurrent unprovoked seizures. Approximately
one in every 100 persons (about 50 million peo-
ple) worldwide are suffering from epilepsy(Iasemidis
et al., 2003). Electroencephalography(EEG) is an im-
portant clinical tool for monitoring, diagnosing and
managing neurological disorders related to epilepsy.
In recent years, there has been an increasing
interest in the application of pattern recognition
(PR) methods for automatic epileptic seizure detec-
tion. Several methods have been developed for han-
dling EEG signals classification, and among these
methods, Multi-layer Perceptron Neural Network
(MLPNN)(Acir et al., 2005; Kalayci and Ozdamar,
1995; Jahankhani et al., 2006; Wang et al., 2005;
¨
Ubeyli, 2009; Ghosh-Dastidar et al., 2007) and Sup-
port Vector Machine (SVM)(Guler and
¨
Ubeyli, 2007;
Chandaka et al., 2009; Lima et al., 2009) are two
widely used classification paradigms.
The general trend in automatic epileptic seizure
detection has focused on high accuracy but has not
considered the time taken to train the classification
models, which should be an important factor of de-
veloping an EEG-based automatic detection device
for epileptic seizures because the device will need to
update its training during use. Therefore some clas-
sification models with high classification accuracy
may not be satisfactory when considering the trade-
off between the classification accuracy and the time
for training the classification models. In our study,
to obtain a balance between high classification accu-
racy and short training time, we investigate the use
of a novel paradigm of learning machine called Ex-
treme Learning Machine (ELM)(Huang et al., 2004).
In recent years, Extreme Learning Machine has been
increasingly popular in classification task due to its
high generation ability and fast learning speed. In
(Wang and Huang, 2005), a classification system is
built using ELM to classify protein sequences with
ten classes of super-families obtained from a domain
database, and its performance is compared with that
of Backpropagation Neural Networks. The results
436
Song Y., Azad S. and Lio P. (2010).
A NEW APPROACH FOR EPILEPTIC SEIZURE DETECTION USING EXTREME LEARNING MACHINE.
In Proceedings of the Third International Conference on Bio-inspired Systems and Signal Processing, pages 436-441
DOI: 10.5220/0002745904360441
Copyright
c
 SciTePress

show ELM greatly outperforms BPNN in terms of
both training time and classification accuracy.(Zhang
et al., 2007) developed an ELM for multi-category
classification in three Cancer Microarray Gene Ex-
pression datasets, and the results reveal that ELM can
not only obtain high classification accuracy but also
avoid problems such as overfitting, local minima, and
improper learning rate. In addition to the field of
Bioinformatics, Extreme Learning Machine has also
been successfully applied to the field of Biosignal
Processing. (Kim et al., 2007) proposed an ELM
based classification scheme for arrhythmia classifi-
cation, and finally achieved 97.5% in average accu-
racy, 97.44% in average sensitivity, 98.46% in aver-
age specificity, and 2.423 seconds in learning time.
Up to now, to the best of our knowledge, there
is no study in the literature related to the assess-
ment of ELM classification performance when ap-
plied specifically to the epileptic/non-epileptic dis-
crimination problem.
The present study is organized as follows: Sec-
tion 2 describes the EEG signals benchmark dataset
used in the experiments. Section 3 presents the mech-
anisms of discrete wavelet transform (DWT), and pro-
vides a description of backpropogation neural net-
work (BPNN) and extreme learning machine (ELM)
classifiers. The feature extraction from DWT and per-
formance comparison of ELM with BPNN is reported
in Section 4. Finally, Section 5 concludes the paper.
2 DATA ANALYZED
In this study, a publicly-available database introduced
in (Andrzejak et al., 2001) has been used. The whole
data is composed of 5 sets (denoted A-E), each con-
taining 100 single-channel EEG data of 23.6s dura-
tion. Sets A and B were taken from surface EEG
recordings of 5 healthy volunteers with eyes open and
closed, respectively. Sets C, D, and E originated from
the EEG archive of presurgical diagnosis. Signals in
Set C were recorded from the hippocampal formation
of the opposite hemisphere of the brain, and signals
in Set D were recorded from within the epileptogenic
zone. While Sets C and D contain only brain activity
measured during seizure free intervals, Set E contains
only seizure activity. All EEG signals were recorded
with the same 128-channel amplifier. The data were
digitized at 173.6 samples per second at 12-bit reso-
lution. Band pass filter was set to 0.53–40 Hz. In the
present work, we classified only two (A and E) of the
complete datasets. The total number of EEG signals
is 200 (100 normal signals and 100 seizure signals).
Each data set has 4096 sampling points.
3 THEORY AND MODELS
3.1 Discrete Wavelet Transform (DWT)
The discrete wavelet transform (DWT) can be thought
of as an extended version of the classic Fourier Trans-
form and instead of working on a single scale, it
works on a multi-scale basis where each signal is de-
composed into several scales, each scale providing
a particular coarseness of the signal. Each phase of
decomposition of a signal is composed of two down
samplers by 2 and two digital filters. Figure 1 gives
the process of Discrete Wavelet Transform. Here in
each phase h(.) is the high-pass filter of that phase
and serves as the discrete mother wavelet; and g(.)
gives the low-pass filter, which acts as the mirror ver-
sion of the corresponding h(.). The down-sampled
outputs of the first low-pass and high-pass filters sup-
ply the approximation A1, and the detail D1, respec-
tively. The first approximation, A1, is further decom-
posed and the procedure is continued. Each low-pass
filter g satisfies the quadrature mirror condition given
in (Guler and
¨
Ubeyli, 2007):
G(Z)G(Z
−
1) + G(−Z)G(−Z
−1
) = 1 (1)
where G(Z) stands for the Z−transform of the fil-
ter g. Its corresponding high-pass filter can be ob-
tained as:
H(Z) = ZG(−Z
−1
) (2)
Therefore, a sequence of filters, in increasing sub-
script of i can be obtained:
G
i
+ 1(Z) = G(Z
2
i
)G
i
(Z), (3)
H
i
+ 1(Z) = H(Z
2
i
)H
i
(Z),i = 0,...,I − 1 (4)
Where initially G
0
(Z) = 1.
For classification purpose two models, namely
Backpropagation neural network and Extreme learn-
ing machine, are discussed in this work.
3.2 Extreme Learning Machine (ELM)
Recently a new learning algorithm called Extreme
Learning Machine (ELM) has been proposed for
single-hidden layer feedforward networks in(Huang
et al., 2004). In comparison with some well-known
classification paradigms such as Support Vector Ma-
chine (SVM) and Backpropagation Neural Network
(BPNN), ELM has some prominent features such as
higher generalization ability, faster learning speed,
A NEW APPROACH FOR EPILEPTIC SEIZURE DETECTION USING EXTREME LEARNING MACHINE
437


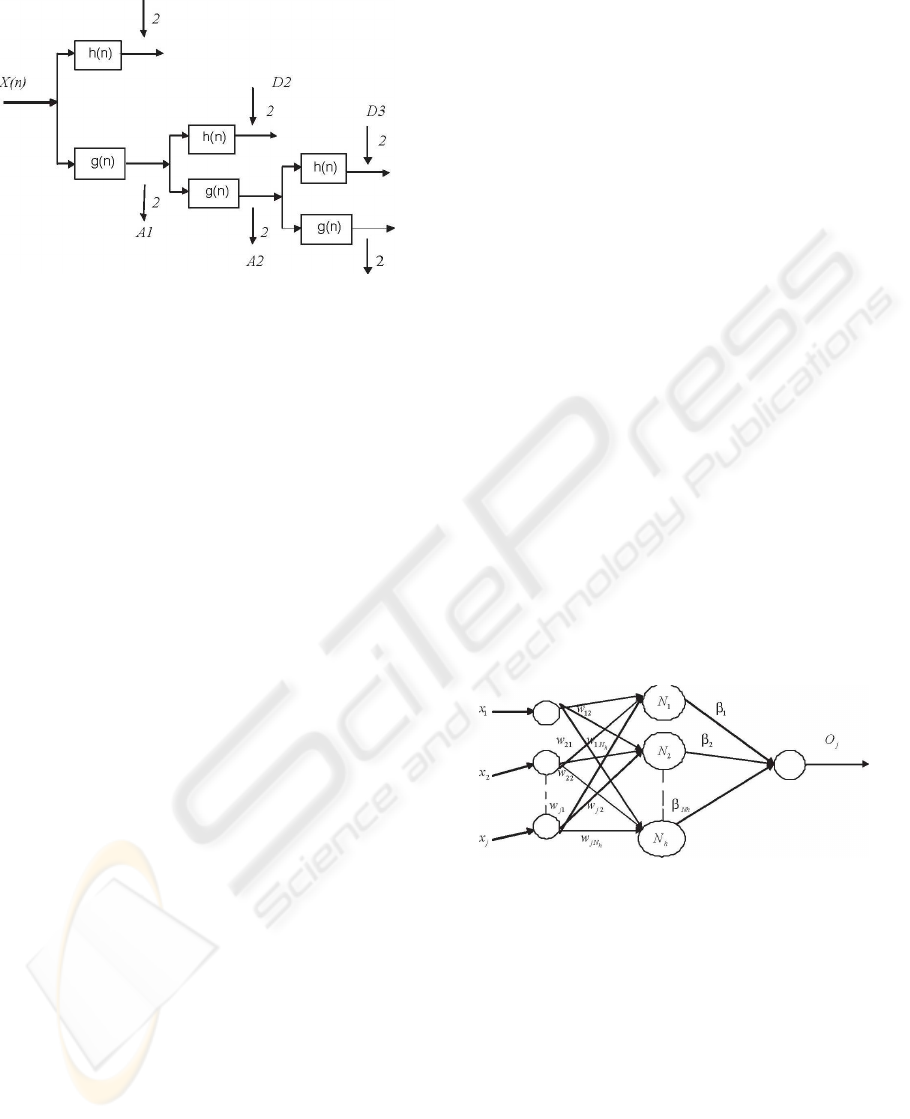
D1 
A3 
Figure 1: Wavelet decomposition of a signal.
and suitability for almost all nonlinear activation
functions, and it can avoid problems like local minima
and improper learning rate, which are usually faced
by traditional learning methods. Figure 2 shows the
structure of ELM. Here, we briefly present the idea
behind ELM.
Suppose learning N arbitrary different instances
(x
i
,t
i
), where x
i
= [x
i1
,x
i2
,...,x
in
]
T
∈ R
n
, and t
i
=
[t
i1
,t
i2
,...,t
im
]
T
∈ R
m
, standard single-layer feedfor-
ward networks with N
h
hidden neurons and activation
function g(x) are mathematically modelled as a linear
system
N
h
∑
i=1
β
i
g(w
i
· x
j
+ b
i
) = o
j
, j = 1,...,N, (5)
where w
i
= [w
i1
,w
i2
,...,w
in
]
T
denotes the weight
vector connecting the ith hidden neuron and the in-
put neuron, β
i
= [β
i1
,β
i2
,...,β
im
]
T
denotes the weight
vector connecting the ith hidden neuron and output
neurons, and b
i
represents the threshold of the ith hid-
den neuron. w
i
∗ x
j
represents the inner product of
w
i
and x
j
. If the single-layer feedforward network
with N
h
hidden neurons with activation function g(x)
is able to approximate N distinct instances (x
i
,t
i
) with
zero error means that
Hβ = T, (6)
where
H(w
1
,...,w
Nh
,b
1
,...,b
Nh
,x
1
,...,x
N
)
=





g(w
1
· x
1
+ b
1
) ... g(w
N
h
· x
1
+ b
N
h
)
. . .
. . .
. . .
g(w
1
· x
N
+ b
1
) ... g(w
N
h
· x
N
+ b
N
h
)





w =






w
T
1
.
.
.
w
T
N
h






N
h
×m
T =





t
T
1
.
.
.
t
T
N





N×m
H is the hidden layer output matrix of the SLFN.
Hence for fixed arbitrary input weights w
i
and the hid-
den layer bias b
i
, training a single-layer feedforward
network equals to discovering a least-squares solution
ˆ
β of the linear system Hβ = T,
ˆ
β = H
†
T is the best
weights, where H
†
is the Moore-Penrose generalized
inverse. In terms of(Huang et al., 2006), Extreme
Learning Machine utilizes such Moore-Penrose in-
verse approach for obtaining good generalization per-
formance with extremely fast learning speed. Unlike
some conventional methods, for example Backprop-
agation algorithm, ELM is able to avoid problems in
tuning control parameters (learning epochs, learning
rate, and so on) and keeping to local minima.
The procedure of ELM for single-layer feedfor-
ward networks is expressed as follows:
1. Choose arbitrary value for input weights w
i
and
biases b
i
of hidden neurons.
2. Calculate hidden layer output matrix H.
3. Obtain the optimal
ˆ
β using
ˆ
β = H
†
T.


Figure 2: The structure of ELM.
4 EXPERIMENTS AND RESULTS
As previously mentioned, the whole dataset is divided
into 5 categories (Sets A-E), each containing 100
EEG signals of 23.6s. In the present work, follow-
ing the work of(Subasi, 2007) and (Chandaka et al.,
2009), we use only Set A (normal EEG signals) and
Set E (epileptic seizure signals) to conduct the com-
putational simulation with ELMs. Therefore, totally
200 EEG signals are obtained, and each EEG signal
contains 4096 sampling points. The discrete wavelet
BIOSIGNALS 2010 - International Conference on Bio-inspired Systems and Signal Processing
438

0 5 10 15 20
−6000
−4000
−2000
0
2000
4000
6000
Number of features
Value of features
0 5 10 15 20
−6000
−4000
−2000
0
2000
4000
6000
Number of features
Value of features
Figure 3: EEG data after feature extraction (Left: Set A. Right: Set E.).
transform (DWT) was used to extract features from
these two EEG data sets, since DWT has ability to
capture transient characteristics in EEG signals and
to localize them in both time and frequency content
accurately according to(Subasi, 2007). After the pro-
cess of multi-resolution decomposition, the EEG sig-
nals were decomposed into details D1-D4 and one
approximation A4. These approximation and details
were reconstructed from the Daubechies 4-wavelet
filter. In order to further reduce the dimensionality of
these extracted features, statistics over these wavelet
coefficients were utilized and four statistical features
was used: (1) Maximum of the wavelet coefficients
in each sub-band; (2) Minimum of the wavelet co-
efficients in each sub-band; (3) Mean of the wavelet
coefficients in each sub-band; (4) Standard deviation
of the wavelet coefficients in each sub-band. Hence,
each EEG data finally consists of 20 features. From
Figure 3, we can see the difference between these
two EEG datasets clearly. The values of features (in
amplitude) extracted from EEG signals in Set E are
much larger than the values of features extracted from
EEG signals in Set A. Hence, these statistical fea-
tures which represent the significant properties of the
two data sets can be utilized for evaluating the perfor-
mance of classifiers.
All the simulations are based on a 2.27 GHz 2-
core CPU with 2 GB memory. In order to compare
the performance of ELM classifiers, we also imple-
mented a backpropagation neural network (BPNN)
based on a Levenberg-Marquardt backpropagation
(LMBP) learning algorithm which is thought of as the
fastest method for training moderate-sized feedfor-
ward neural networks according to(Hagan and Men-
haj, 1994). For the BPNN and ELM, all of the in-
put value were normalized in the range of [-1,1]. The
weight vector w
i
and the threshold b
i
of ELM were
randomly generated in the range of [-1,1]. The num-
ber of hidden neurons in BPNN was set to 25 accord-
ing to (Subasi, 2007) and the number of hidden neu-
rons in ELM was set to 20. The performance of the
BPNN and ELM algorithms was evaluated by the fol-
lowing measures:
• Sensitivity: number of true positive detec-
tions/number of actually positive subjects.
Sensitivity = TP/(TP+ FN).
• Specificity: number of true negative detec-
tions/number of actually negative subjects.
Specificity = TN/(TN + FP).
• Classification Accuracy: number of correct detec-
tions/total number of subjects.
Classification Accuracy = (TP + TN)/(TP +
TN + FP+ FN).
• Learning time: A measure of the time spent in
training classifiers.
Among these 200 EEG data (100 normal signals
and 100 epileptic seizure signals), half of the normal
EEG signals and half of the epileptic EEG signals
were used for training, and the rest for testing.
After training BPNN and ELM, the test data was
used to evaluate the performance of these two classifi-
cation algorithms. Classification results of the BPNN
and the ELM classifiers are displayed by confusion
matrices. The confusion matrices demonstrating clas-
sification results of two classifiers are given in Table
1. In terms of the confusion matrices, 5 epileptic sub-
jects were classified incorrectly by the BPNN classi-
fier as normal subjects, however only 2 epileptic sub-
jects were classified incorrectly using the ELM clas-
sifier. Both classifiers identified correctly all normal
subjects. In order to calculate the average test per-
formance of two classifiers, the classification experi-
ment was repeated for ten times and all the simulation
results were averaged over 10 trials. The results are
given in Table 2.
A NEW APPROACH FOR EPILEPTIC SEIZURE DETECTION USING EXTREME LEARNING MACHINE
439

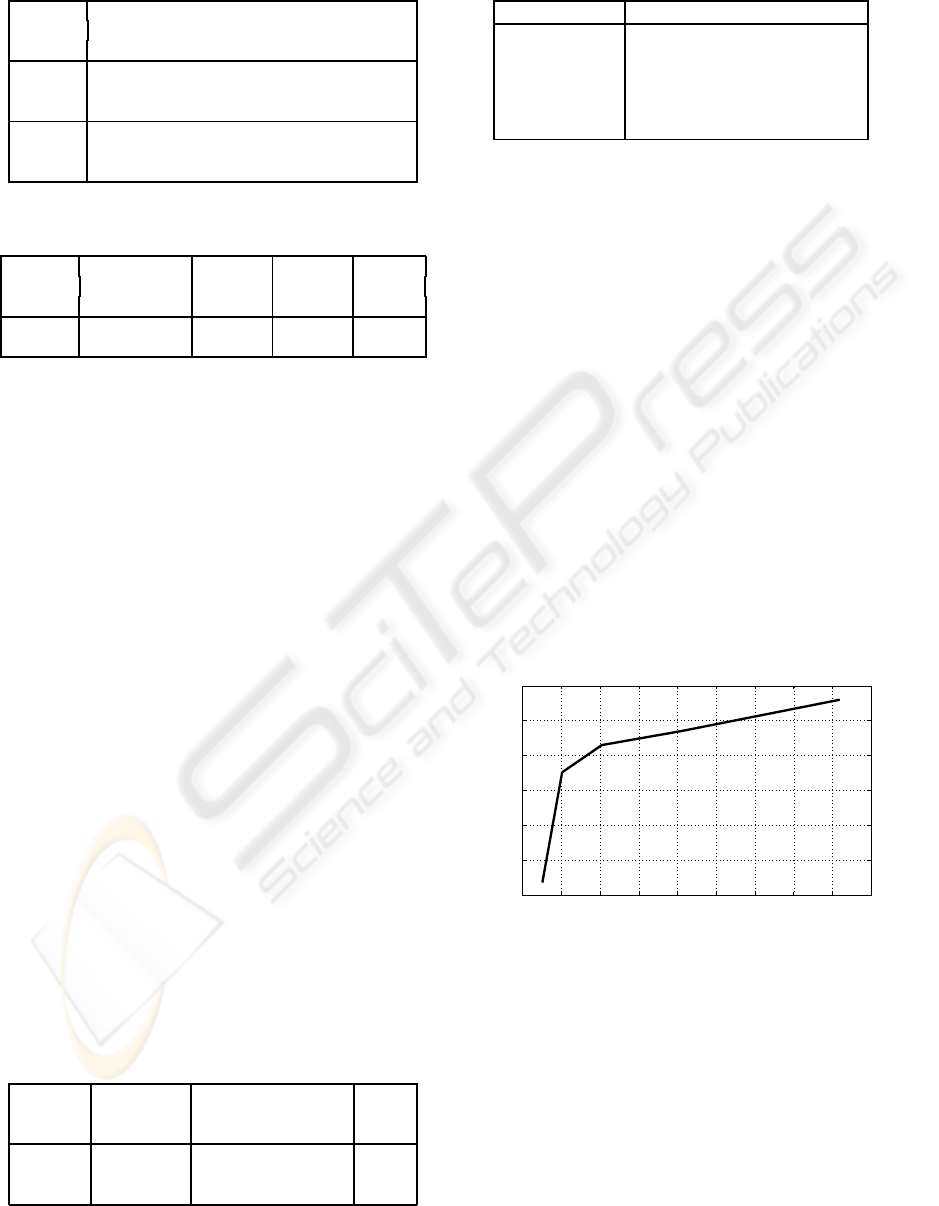
Table 1: Confusion matrices of the classifiers.
Output result
Classifiers Desired result
Epileptic Normal
Epileptic 45 5
BPNN
Normal 0 50
Epileptic 48 2
ELM
Normal 0 50
Table 2: Performance comparison of ELM and BPNN.
Average Average Average Average
Classifiers Learning Sensitivity Specificity Accuracy
Time(Seconds) (%) (%) (%)
ELM 0.0187 93.6 100 96.8
BPNN 52.9969 90.6 100 95.3
As quoted in Table 2, it is clear that the ELM
classifier outperforms the BPNN classifier in its av-
erage classification accuracy of the EEG signals. It
is shown that performance rate with ELM is 96.8%
whereas with BPNN it is 95.3%. The ELM classifier
recognized precisely all the normal and epileptic sub-
jects with sensitivity 93.6% and specificity 100%, fol-
lowed by the BPNN classifier with sensitivity 90.6%
and specificity 100%. Thus the ELM classifier can
obtain better generalization than the BPNN classifier.
In addition, the learning time of the ELM classifier
is 0.0187s while the learning time of the BPNN clas-
sifier is 52.9969s. The ELM classifier can run 2834
times faster than the BPNN classifier. Hence, in the
case of real-time implementation of epilepsy diagno-
sis support system, ELM classifiers are more appro-
priate than BPNN classifiers.
In Table 3, we present a comparison in classi-
fication performance achieved by different methods.
we have quoted results from our present proposed
method (Wavelet-ELM) and also from recently re-
ported in(Subasi, 2007) and (Chandaka et al., 2009).
The datasets used in these experiments are the same
(Set A and Set E). It is shown in the table that our
method generates better classification accuracy com-
Table 3: Comparison of statistical parameters of various
classification algorithms.
Type of ME model Cross-correlation Wavelet
Classifier (Subasi2007) SVM(Chandaka2009) ELM
(%) (%) (%)
Specificity 94 100 100
Sensitivity 95 92 93.6
Accuracy 94.5 95.96 96.8
Table 4: Effect of change in window size.
Window Size Average Test Accuracy (%)
4096 96.80
2048 96.35
1024 96.15
512 95.76
256 94.18
pared with those of others.
In the next step of the experiment, we further in-
vestigate the generalization of our Wavelet-ELM clas-
sification scheme by varying the length of EEG sig-
nals. Four rectangular windows are formed, using
2048, 1024, 512 and 256 sampling points respec-
tively, such that each EEG signal is divided into 2,
4, 8, 16 small segments. Hence, in Case Study 2,
there are 200 EEG signals with 2048 sampling points
in each set; in Case Study 3, there are 400 EEG sig-
nals with 1024 sampling points in each set; in Case
Study 4, there are 800 EEG signals with 512 sampling
points in each set; in Case Study 5, there are 1600
EEG signals with 256 sampling points in each set. In
all case studies, we still use 50% EEG data from each
set for training and the remaining 50% for testing. Ta-
ble 4 describes the average test accuracy over 10 trials
using ELM classifiers for every case study. It is ob-
vious from the results that the larger the window size,
the greater the average test accuracy. Figure 4 sum-
marises the obtained results.
0 500 1000 1500 2000 2500 3000 3500 4000 4500
94
94.5
95
95.5
96
96.5
97
Window Size
Average Tesing Accuracy of ELM (%)
Figure 4: The relationship between the generalization per-
formance and window size.
BIOSIGNALS 2010 - International Conference on Bio-inspired Systems and Signal Processing
440

5 CONCLUSIONS
In this paper, we have investigated the Wavelet-
Extreme Learning Machine classification scheme for
identifying epileptic seizures. Using statistical fea-
tures extracted from the DWT sub-bands of EEG sig-
nals, ELM and BPNN classifiers are built and com-
pared according to their test accuracy and learning
time. The proposed system using the ELM classifier
can achieve test accuracy as high as 96.8%, as com-
pared to BPNN classifier and two recently-proposed
methods, where the test accuracies are 95.3%, 94.5%
and 95.96% respectively. In addition, this study also
shows that the ELM classifier needs much less learn-
ing time compared to the stand-alone BPNN classi-
fier for the task of epileptic seizure detection, which
demonstrates its potential for real-time implementa-
tion in an epilepsy diagnosis support system.
ACKNOWLEDGEMENTS
This work is financed by the EU 6 Framework
Programme Project: Measuring and Modelling
Relativistic-Like Effects in Brain and NCSs.
REFERENCES
Acir, N., Oztura, I., Kuntalp, M., Baklan, B., and Guzelis,
C. (2005). Automatic detection of epileptiform events
in EEG by a three-stage procedure based on artificial
neural networks. IEEE Transactions on Biomedical
Engineering, 52(1):30–40.
Andrzejak, R., Lehnertz, K., Mormann, F., Rieke, C.,
David, P., and Elger, C. (2001). Indications of non-
linear deterministic and finite-dimensional structures
in time series of brain electrical activity: Dependence
on recording region and brain state. Physical Review
E, 64(6):61907.
Chandaka, S., Chatterjee, A., and Munshi, S. (2009). Cross-
correlation aided support vector machine classifier for
classification of EEG signals. Expert Systems With
Applications, 36(2P1):1329–1336.
¨
Ubeyli, E. (2009). Statistics over features: EEG sig-
nals analysis. Computers in Biology and Medicine,
39(8):733–741.
Ghosh-Dastidar, S., Adeli, H., and Dadmehr, N. (2007).
Mixed-band wavelet-chaos-neural network method-
ology for epilepsy and epileptic seizure detec-
tion. IEEE Transactions on Biomedical Engineering,
54(9):1545–1551.
Guler, I. and
¨
Ubeyli, E. (2007). Multiclass support vector
machines for EEG-signals classification. IEEE Trans-
actions on Information Technology in Biomedicine,
11(2):117–126.
Hagan, M. and Menhaj, M. (1994). Training feedforward
networks with the marquardt algorithm. IEEE trans-
actions on Neural Networks, 5(6):989–993.
Huang, G., Zhu, Q., and Siew, C. (2004). Extreme learn-
ing machine: a new learning scheme of feedforward
neural networks. In 2004 IEEE International Joint
Conference on Neural Networks, 2004. Proceedings,
volume 2.
Huang, G., Zhu, Q., and Siew, C. (2006). Extreme learning
machine: theory and applications. Neurocomputing,
70(1-3):489–501.
Iasemidis, L., Shiau, D., Chaovalitwongse, W., Sackellares,
J., Pardalos, P., Principe, J., Carney, P., Prasad, A.,
Veeramani, B., and Tsakalis, K. (2003). Adaptive
epileptic seizure prediction system. IEEE Transac-
tions on Biomedical Engineering, 50(5):616–627.
Jahankhani, P., Kodogiannis, V., and Revett, K. (2006).
EEG signal classification using wavelet feature ex-
traction and neural networks. In IEEE John Vincent
Atanasoff 2006 International Symposium on Modern
Computing, 2006. JVA’06, pages 120–124.
Kalayci, T. and Ozdamar, O. (1995). Wavelet preprocess-
ing for automated neural network detection of EEG
spikes. IEEE Engineering in Medicine and Biology
Magazine, 14(2):160–166.
Kim, J., Shin, H., Lee, Y., and Lee, M. (2007). Algo-
rithm for classifying arrhythmia using extreme learn-
ing machine and principal component analysis. In
Engineering in Medicine and Biology Society, 2007.
EMBS 2007. 29th Annual International Conference of
the IEEE, pages 3257–3260.
Lima, C., Coelho, A., and Chagas, S. (2009). Automatic
EEG signal classification for epilepsy diagnosis with
relevance vector machines. Expert Systems With Ap-
plications, 36(6):10054–10059.
Subasi, A. (2007). EEG signal classification using wavelet
feature extraction and a mixture of expert model. Ex-
pert Systems with Applications, 32(4):1084–1093.
Wang, B., Jun, L., Bai, J., Peng, L., Li, Y., and Li, G.
(2005). EEG recognition based on multiple types of
information by using wavelet packet transform and
neural networks. In Proc. 2005 IEEE Engineering
in Medicine and Biology 27th Annual Conference,
Shanghai, China, pages 5377–5380.
Wang, D. and Huang, G. (2005). Protein sequence classifi-
cation using extreme learning machine. In 2005 IEEE
International Joint Conference on Neural Networks,
2005. IJCNN’05. Proceedings, volume 3.
Zhang, R., Huang, G., Sundararajan, N., and Saratchan-
dran, P. (2007). Multicategory classification using
an extreme learning machine for microarray gene ex-
pression cancer diagnosis. IEEE/ACM Transactions
on Computational Biology and Bioinformatics, pages
485–495.
A NEW APPROACH FOR EPILEPTIC SEIZURE DETECTION USING EXTREME LEARNING MACHINE
441